Javier works each weekend at an animal shelter. He earns $8 an hour. He is saving his earnings to go on a ski trip that costs $190.
Becca says that Javier must work at least 6 more hours to have enough money to go on the ski trip. Her work is shown below. Choose True or False about each statement
Becca's solution included all of the hours Javier worked on both weekends. (TRUE OR FALSE?)
Javier worked a total of 23 hours on both weekends. (TRUE OR FALSE?)
Javier earns $198 for 24 hours of work. (TRUE OR FALSE?)
Javier only needs to work one more hour to have enough money for his trip. (TRUE OR FALSE?)
Answers
Answer:
Becca's solution included all of the hours Javier worked on both weekends.Step-by-step explanation:
Javier needs to work at least 6 more hours. He will earn:
6*8 = $48He has already got:
$190 - $48 = $142He worked:
142/8 = 18 hours (rounded)Total he will have worked:
18 + 6 = 24 hoursAnswer choices:
Becca's solution included all of the hours Javier worked on both weekends.
TRUEJavier worked a total of 23 hours on both weekends.
FALSE. 23*$8 = $184 < $190Javier earns $198 for 24 hours of work.
FALSE. 24*8 = $192Javier only needs to work one more hour to have enough money for his trip.
FALSE. Becca says 6 more hours required.Related Questions
Lindsey has two sisters. The sum of the girls' ages is 13. The product of their ages is 36. How old is each sister?
Answers
Answer:
The product of their ages is 36
The sum of the girls age is 13
two sister=?
13 by 36
26
x=13-y — (1)
xy=36 — (2)
Sub (1) into (2)
y(13-y)=36
y^2-13y+36=0
y=9 or 4 (quadratic formula)
Sub y=9,
x=4
Sub y=4,
x=9
40 POINTS
ASAP PLEASE HELP
Which experimental result best matches the theoretical probability of the event?
A.
Liza has an 8-sided number solid that is numbered 1 through 8. She rolls it 56 times and records her results. The results show that an even number was rolled 14 times.
B.
Mia has a bag that contains a letter block for each of the 26 letters of the alphabet. She draws a letter block from the bag, writes down the letter, and puts the block back in the bag. She repeats this 26 times. The results show that she drew a vowel (A, E, I, O, or U) 6 times.
C.
Sarah spins a spinner with 6 equal-sized sections of different colors and records the color on which the spinner lands. She repeats this 24 times. The results show that the spinner landed on red 10 times.
D.
Charlie draws a number tile from a box containing the numbers 1 to 10, writes down the number, and puts the tile back in the box. He repeats this 40 times. The results show that the number 5 was drawn 10 times.
Answers
Answer:
Mia has a bag that contains a letter block for each of the 26 letters of the alphabet. She draws a letter block from the bag, writes down the letter, and puts the block back in the bag. She repeats this 26 times. The results show that she drew a vowel (A, E, I, O, or U) 6 times.
Step-by-step explanation:

The best match is Mia has a bag that contains a letter block for each of the 26 letters of the alphabet option (B) is correct.
What is probability?It is defined as the ratio of the number of favorable outcomes to the total number of outcomes, in other words, the probability is the number that shows the happening of the event.
It is given that:
The theoretical probability of the event?
As we know,
The area of mathematics that deals with probability are called probability theory.
Probability theory tackles the idea in a rigorously mathematical way by expressing it through a set of axioms, despite the fact that there are many distinct probability interpretations.
Thus, the best match is Mia has a bag that contains a letter block for each of the 26 letters of the alphabet option (B) is correct.
Learn more about the probability here:
brainly.com/question/11234923
#SPJ5
jessica made $234 for 13 hours of work. At the same rate, how many hours would she have to work to make $162?
Answers
Answer: 9 hours
We would get:
1 hour of work = $18
162 divided by 18 = 9
So she would have to work 9 hours
Answer:
9 hours
Step-by-step explanation:
Step One: A rate is the same thing as ratio. This just means that there is a proportion. For example, for every 3 dogs, there are 4 cats. This would mean that for 6 dogs there are 8 cats, and so on.
Step Two: Okay, because these numbers are larger, it is easiest to scale it back to one. The proportion or rate given is $234/13 hours. We would divide by 13 to get it to 1: $18/1 hour. The proportion is usually a decimal, but these numbers happen to divide nicely.
Step Three: Now, we can do 162/18 to see what the scale is, or how much times larger it is: 162/18=9.
Step Four: Lastly, just do 1 times 9, which tells it is 9 hours. To check the work, make sure 9 is less than the original proportion; it should take less time to make less money. 9 is less than 13, so this is the answer!
Find \int(3 x^{4}+6 x^{5}) d x 1+C
Answers
The integral of (3x^4 + 6x^5) with respect to x is (3/5)x^5 + (6/6)x^6 + C, where C is the constant of integration. To find the integral of the given function, we apply the power rule of integration.
For each term, we add 1 to the power and divide the coefficient by the new power. The constant of integration, denoted as C, is added at the end. For the term 3x^4, we add 1 to the power to get x^5. We then divide the coefficient 3 by 5 to get (3/5)x^5. For the term 6x^5, we add 1 to the power to get x^6. We divide the coefficient 6 by 6 to get (6/6)x^6, which simplifies to x^6.
Combining the results, we obtain the integral of (3x^4 + 6x^5) as (3/5)x^5 + (6/6)x^6. Finally, we add the constant of integration C, which accounts for the possibility of multiple antiderivatives having the same derivative.Therefore, the integral of (3x^4 + 6x^5) with respect to x is given by (3/5)x^5 + (6/6)x^6 + C.
Learn more about coefficient here:- brainly.com/question/13431100
#SPJ11
How to find the dimensions of the hoses in hydraulics (for
advance and return).
force of advance = 293 KN
force of return = 118KN
Answers
The diameter of the hose for return is approximately 22.7 mm.
In hydraulics, hoses are a crucial part of the system as they transfer the hydraulic fluid that transmits power to the actuators. In order to select the right hoses, it is important to consider factors such as the flow rate, pressure drop, and the length of the hoses.
Q = (A x V)/60
Where:
Q = flow rate in liters per minute (lpm)
A = area of the hose in square millimeters (mm²)
V = velocity of the fluid in meters per second (m/s)
60 = conversion factor from seconds to minutes
The force of advance and return can be used to determine the pressure of the system. We can then use the pressure drop and the length of the hoses to find the flow rate. Finally, we can use the flow rate to find the area of the hoses.
For the force of advance:
Pressure = force/area
Area = force/pressure
Assuming a pressure drop of 5 bar and a hose length of 10 meters, we can find the flow rate as follows:
Flow rate = (1000 x 293)/((5 x 10) + 1000)
Flow rate = 54.98 lpm
Using the formula Q = (A x V)/60, we can find the area of the hose as follows:
A = (Q x 60)/V
Assuming a fluid velocity of 4 m/s, we get:
A = (54.98 x 60)/(4 x π x (0.0127/2)²)
A = 1005.2 mm²
Therefore, the diameter of the hose for advance is approximately 36.0 mm.
For the force of return:
Pressure = force/area
Area = force/pressure
Assuming a pressure drop of 5 bar and a hose length of 10 meters, we can find the flow rate as follows:
Flow rate = (1000 x 118)/((5 x 10) + 1000)
Flow rate = 22.11 lpm
Using the formula Q = (A x V)/60, we can find the area of the hose as follows:
A = (Q x 60)/V
Assuming a fluid velocity of 4 m/s, we get:
A = (22.11 x 60)/(4 x π x (0.0127/2)²)
A = 404.1 mm²
Therefore, the diameter of the hose for return is approximately 22.7 mm.
To know more about diameter, visit:
https://brainly.com/question/32968193
#SPJ11
solve
−2(x−7)+3(x+5)=x+9
Answers
Answer:
no solutions
Step-by-step explanation:
−2(x−7)+3(x+5)=x+9
Distribute
-2x +14 +3x +15 = x+9
Combine like terms
x + 29 = x+9
Subtract x from each side
x+29 -x = x+9-x
29 = 9
This is never true so there are no solutions
Answer:
It is wrong Problem
Step-by-step explanation:
-2x+14+3x+15=x+9
x+29=x+9
????
A line includes the points (3, 1) and (5, 7). What is its equation in slope-intercept form?
Write your answer using integers, proper fractions, and improper fractions in simplest form.
Answers
Answer:
Y=3x - 8
Step-by-step explanation:
Slope-intercept is Y=mx +b
Solve for m using the formula (y₂ - y₁) / (x₂ - x₁)
so (7-1) / (5-3)
Solve inside paratheses to get 6/2. Simplify to 3
Solve for b by plugging in our first points (3,1)
1 = 3(3) + b
1 = 9 + b
-8 = b
Which equation represents the polar form of x2 (y 4)2 = 16? r = 8sin(θ) r = 8cos(θ) r = –8sin(θ) r = –8cos(θ)
Answers
solve for the variable. if necessary round to the nearest tenth.a) 6b) 30c) 14.7d) 27

Answers
Allura, this is the solution:
As you can see we have two right triangles in the figure:
Therefore,
Step 1: Let's calculate the hypotenuse of the left triangle, as follows:
c² = a² + b²
c² = 12² + 18²
c²= 144 + 324
c² = 468
c = 21.63
Step 2: Let's calculate the sides of the right triangle on the right, this way:
Leg 1 = 21.63
Leg 2 = x
Hypotenuse = 12 + y
Height of the right triangle = 18
In consequence, to find the value of the hypotenuse and y, we have:
c = 21.63²/√21.63² - 18²
c = 468/√468 - 324
c = 468/12
c = 39
Step 3: Now, we can solve for y, this way:
39 = 12 + y
y = 39 - 12
y = 27
The correct answer is D. 27
find the least common multiple of the following polynomials 9(x 2)(2x-1) and 3(x 2)
Answers
The LCM of the given polynomials is 27x²(2x - 1).
In order to find the least common multiple (LCM) of the following polynomials 9(x²)(2x - 1) and 3(x²), we need to factorize the given polynomials. And then take the product of the highest power of each factor that appears in the polynomials. We can find the LCM of the given polynomials using the following steps:
Step 1: Factorize the given polynomials9(x²)(2x - 1) can be written as 9 × x² × (2x - 1)3(x²) can be written as 3 × x²
Step 2: Write down the factors of each polynomial9(x²)(2x - 1) = 3 × 3 × x² × (2x - 1)3(x²) = 3 × x²
Step 3: Determine the highest power of each factor that appears in the polynomials9(x²)(2x - 1) contains the factor 3 once and x² twice3(x²) contains the factor 3 once and x² once the LCM is the product of the highest power of each factor. Thus, the LCM of 9(x²)(2x - 1) and 3(x²) is given by:
LCM = 3 × 3 × x² × (2x - 1) = 27x²(2x - 1)Thus, the LCM of the given polynomials is 27x²(2x - 1).
Learn more about polynomials:https://brainly.com/question/1496352
#SPJ11
Look at the equation below f(x)= x³ + x² - 10x + 8 Find the real roots using the method a. bisection. b. Newton-Raphson c. Secant With stop criteria is relative error = 0.0001%. You are free to make a preliminary estimate. Show the results of each iteration to the end.
Answers
a. Bisection Method: To use the bisection method to find the real roots of the equation f(x) = x³ + x² - 10x + 8, we need to find an interval [a, b] such that f(a) and f(b) have opposite signs.
Let's make a preliminary estimate and choose the interval [1, 2] based on observing the sign changes in the equation.
Iteration 1: a = 1, b = 2
c = (a + b) / 2
= (1 + 2) / 2 is 1.5
f(c) = (1.5)³ + (1.5)² - 10(1.5) + 8 ≈ -1.375
ince f(c) has a negative value, the root lies in the interval [1.5, 2].
Iteration 2:
a = 1.5, b = 2
c = (a + b) / 2
= (1.5 + 2) / 2 is 1.75
f(c) = (1.75)³ + (1.75)² - 10(1.75) + 8 ≈ 0.9844
Since f(c) has a positive value, the root lies in the interval [1.5, 1.75].
Iteration 3: a = 1.5, b = 1.75
c = (a + b) / 2
= (1.5 + 1.75) / 2 is 1.625
f(c) = (1.625)³ + (1.625)² - 10(1.625) + 8 is -0.2141
Since f(c) has a negative value, the root lies in the interval [1.625, 1.75].
Iteration 4: a = 1.625, b = 1.75
c = (a + b) / 2
= (1.625 + 1.75) / 2 is 1.6875
f(c) = (1.6875)³ + (1.6875)² - 10(1.6875) + 8 which gives 0.3887.
Since f(c) has a positive value, the root lies in the interval [1.625, 1.6875].
Iteration 5: a = 1.625, b = 1.6875
c = (a + b) / 2
= (1.625 + 1.6875) / 2 is 1.65625
f(c) = (1.65625)³ + (1.65625)² - 10(1.65625) + 8 is 0.0873 .
Since f(c) has a positive value, the root lies in the interval [1.625, 1.65625].
Iteration 6: a = 1.625, b = 1.65625
c = (a + b) / 2
= (1.625 + 1.65625) / 2 which gives 1.640625
f(c) = (1.640625)³ + (1.640625)² - 10(1.640625) + 8 which gives -0.0638.
Since f(c) has a negative value, the root lies in the interval [1.640625, 1.65625].
teration 7: a = 1.640625, b = 1.65625
c = (a + b) / 2
= (1.640625 + 1.65625) / 2 results to 1.6484375
f(c) = (1.6484375)³ + (1.6484375)² - 10(1.6484375) + 8 is 0.0116
Since f(c) has a positive value, the root lies in the interval [1.640625, 1.6484375].
Continuing this process, we can narrow down the interval further until we reach the desired level of accuracy.
b. Newton-Raphson Method: The Newton-Raphson method requires an initial estimate for the root. Let's choose x₀ = 1.5 as our initial estimate.
Iteration 1:
x₁ = x₀ - (f(x₀) / f'(x₀))
f(x₀) = (1.5)³ + (1.5)² - 10(1.5) + 8 which gives -1.375.
f'(x₀) = 3(1.5)² + 2(1.5) - 10 which gives -1.25.
x₁ ≈ 1.5 - (-1.375) / (-1.25) which gives 2.6.
Continuing this process, we can iteratively refine our estimate until we reach the desired level of accuracy.
c. Secant Method: The secant method also requires two initial estimates for the root. Let's choose x₀ = 1.5 and x₁ = 2 as our initial estimates.
Iteration 1: x₂ = x₁ - (f(x₁) * (x₁ - x₀)) / (f(x₁) - f(x₀))
f(x₁) = (2)³ + (2)² - 10(2) + 8 gives 4
f(x₀) = (1.5)³ + (1.5)² - 10(1.5) + 8 gives -1.375
x₂ ≈ 2 - (4 * (2 - 1.5)) / (4 - (-1.375)) gives 1.7826
Continuing this process, we can iteratively refine our estimates until we reach the desired level of accuracy.
To know more about Bisection Method visit-
brainly.com/question/32563551
#SPJ11
given an array arr of n positive integers the following operations can be performed 0 or more times
Answers
The minimum number of operations required is `15`.
Given an array `arr` of `n` positive integers, the following operations can be performed 0 or more times:
select any two different indices `i` and `j` such that `1 ≤ i < j ≤ n`, and subtract `1` from each of the `arr[i]` and `arr[j]`.
The objective is to make all the elements of `arr` equal, or determine that it is impossible to do so.
The minimum number of operations required to achieve this is `n - 1`.
Therefore, the minimum possible value of `n` is `2`, for which the array `arr` must have only two elements, i.e., `arr = [x, x]` for some positive integer `x`.
For `n > 2`, we can approach the problem as follows:
Calculate the sum `sum` of all the elements in the array `arr`.
Then, we can divide this sum by `n` to get the target value `x` that we want all the elements to be equal to.
However, this is only possible if `n` divides `sum` exactly.
Otherwise, it is impossible to make all the elements equal through the given operations.
The minimum number of operations required to make all the elements equal is equal to the sum of the absolute differences between each element and the target value `x`.
That is: \sum_{i=1}^{n} |arr[i] - x|
For example, suppose `arr = [5, 10, 20]`.
Then, we have `sum = 5 + 10 + 20 = 35`.
To make all the elements equal, we want each element to be `x = sum/n = 35/3`.
However, since `n` does not divide `sum`, this is impossible.
Therefore, we need to find the minimum number of operations required to make all the elements equal to some value between `5` and `20`.
If we choose `x = 10`, then the absolute differences between each element and `x` are: |5 - 10| + |10 - 10| + |20 - 10| = 5 + 0 + 10 = 15
Therefore, the minimum number of operations required is `15`.
Learn more about operations from the given link;
https://brainly.com/question/30415374
#SPJ11
Given an array arr of n positive integers, the following operations can be performed 0 or more times:
Choose an index I where 0<=i<n
choose 2 integers, x and y, such that x+y=arr[i]
replace arr[i] with two elements, the two values x and y
Determine the minimum number of operations required to sort the array.
why is water a necessary element for our bodies to function properly? summarize what can happen if a person becomes dehydrated.
Answers
Aid in the elimination of metabolic byproducts, excess electrolytes (for example, salt and potassium), and urea, a waste product generated during the digestion of ingested protein. Sweating helps to regulate body temperature.
Why is water a necessary element for our bodies to function properly?Maintain a regular body temperature. Joints should be lubricated and cushioned. Safeguard your spinal cord and other delicate structures. Wastes can be eliminated by urine, sweat, and bowel motions. Dehydration can also cause a decrease in strength and stamina. It is the most common cause of heat exhaustion. At this point, you should be able to reverse dehydration by consuming extra fluids. Chronic dehydration might impair your kidney function and raise your risk of kidney stones. Water also helps with normal bowel function, muscular performance, and clean, young skin. Failure to drink enough water, on the other hand, can result in dehydration and negative symptoms such as weariness, headache, reduced immunity, and dry skin.
Here,
Assist in the elimination of metabolic byproducts, excess electrolytes (for example, salt and potassium), and urea, a waste product generated during the digestion of ingested protein. Sweating regulates body temperature.
To know more about necessity of water,
https://brainly.com/question/20593274
#SPJ4
PLEASE HELP ME! I REALLY NEED SOME HELP!!

Answers
Answer:
a
Step-by-step explanation:
If the lines DE and BC were parallel then
Δ ADE and Δ ABC would be similar and the ratios of corresponding sides would be equal, that is
\(\frac{AD}{AB}\) = \(\frac{AE}{AC}\) , substituting values
\(\frac{4}{10}\) = \(\frac{6}{14}\)
but
\(\frac{4}{10}\) ≠ \(\frac{6}{14}\)
That is 4 : 10 ≠ 6 : 14 → a
Which one of the following statements is not true concerning PivotTables in Excel? O a. PivotTables are also known as crosstabulation tables. b. PivotTables summarize data for two variables. c.PivotTables can be built using data arrayed in rows. d. PivotTables are interactive.
Answers
The statement that is not true concerning PivotTables in Excel is b. PivotTables summarize data for two variables. PivotTables can summarize data for multiple variables, not just two.
PivotTables allow you to analyze and summarize data from various perspectives, including multiple variables, by grouping, filtering, and calculating values based on different criteria. They provide flexibility in summarizing and organizing data in a tabular format, making it easier to extract insights and perform data analysis efficiently.
To know more about Pivot table, visit:
https://brainly.com/question/29817099
#SPJ11
The side length of the square shown is tripled.
3 cm
Which percent of increase is greater the percent of increase for the perimeter of the square or the percent of increase for the area? How
much greater?
The percent of increase for the
is greater
It is
% greater
Answers
Answer:
The percentage increase for the area is greater
It is 600% greater
Step-by-step explanation:
Here, we have a square of side length 3 cm
The area of the square is L^2 = 3^2 = 9 cm^2
Perimeter of the square = 4L = 4 * 3 = 12 cm
When we triple the length of the square, its new length becomes 3 * 3 = 9 cm
Area here will be 9 * 9 = 81 cm^2
Perimeter = 4 L = 4 * 9 = 36cm
To calculate percentage change, we use the formula;
(new value - old value)/old value * 100%
For the perimeter;
(36-12)/12 * 100% = 24/12 * 100% = 2 * 100% = 200%
For the area;
(81-9)/9 * 100% = 72/9 * 100% = 8 * 100% = 800%
The percentage increase of the area is greater
How much greater? 800% - 200% = 600%
find the sum (3x^2-2x+1) + (4x^2 + 3x + 2)
Answers
Answer:
7x^2+x+3
Step-by-step explanation:
collect the like terms:
3x^2-2x+1+4x^2+3x+2
7x^2-2x+1+3x+2
7x^2+x+1+2
solution:
7x^2+x+3
Describe how to determine f(x) and g(x) when x=5

Answers
Answer:
brainly is the best study app in the world
Help is this correct (this is 12 year old math)
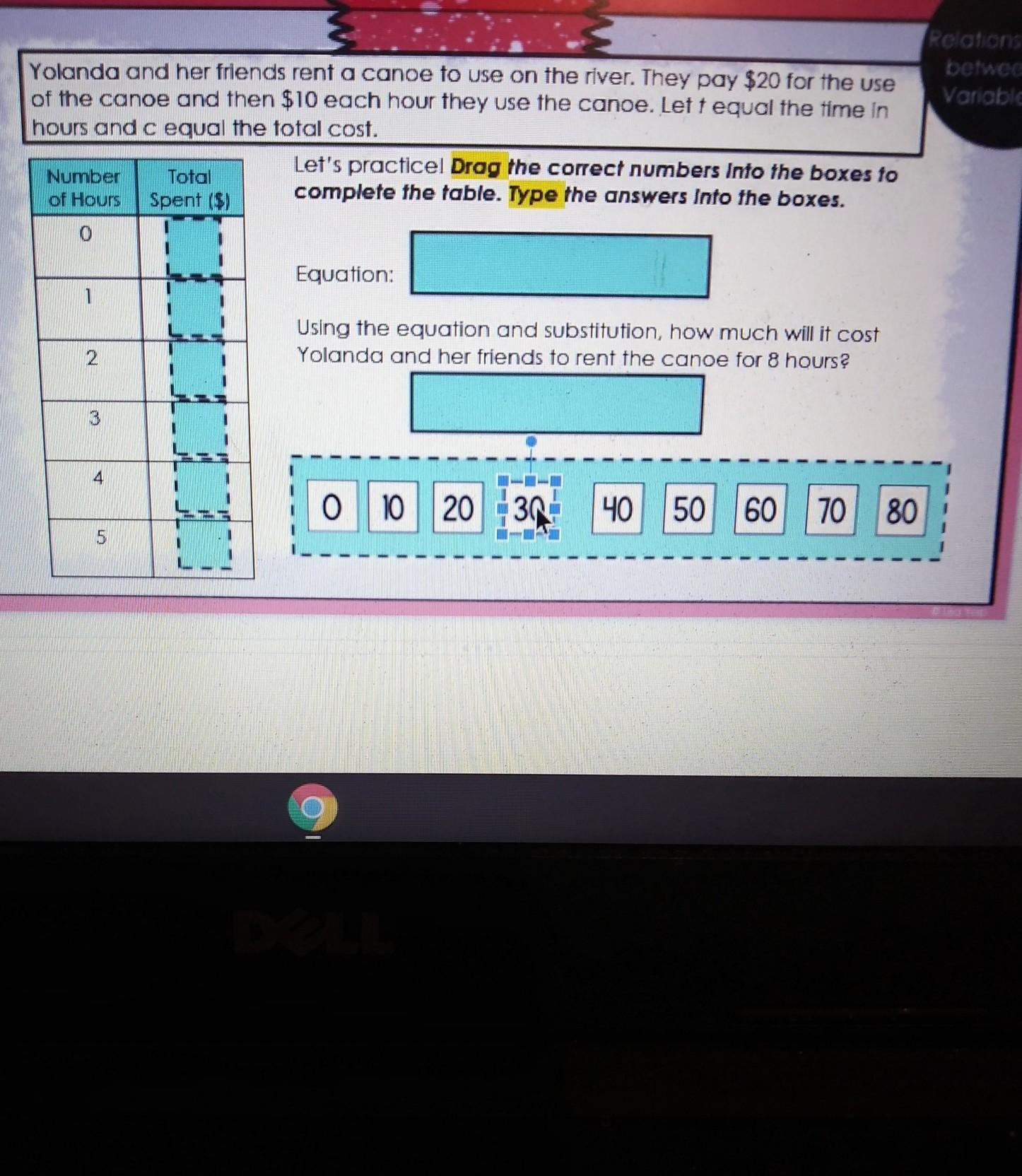
Answers
Answer:
Yes you are correct good job:D
Step-by-step explanation:
PLS HELP ASAP!!!
This figure is made up of a rectangle and parallelogram.
What is the area of this figure?
Enter your answer in the box. Do not round any side lengths.
__ units²
Answers
The area of figure is,
⇒ 26 units²
What is mean by Rectangle?A rectangle is a two dimension figure with 4 sides, 4 corners and 4 right angles. The opposite sides of the rectangle are equal and parallel to each other.
Here, The given figure is made up of a parallelogram and a rectangle.
Hence, The area of the parallelogram is
⇒ Base × Height
Here, The base of the parallelogram is 6 units (Just count the boxes).
And, The height is also 1 unit.
This implies that the area of the parallelogram is
⇒ Base × Height
⇒ 6 × 1
⇒ 6 units²
And, To find the area of the rectangle, we need to find the width and the length using the distance formula or the Pythagoras Theorem.
Using the Pythagoras Theorem as;
⇒ l² = a² + b²
⇒ l² = 2² + 6²
⇒ l² = 4 + 36
⇒ l² = 40
⇒ l = 2√10
And, We get;
⇒ w² = 1² + 3²
⇒ w² = 1 + 9
⇒ w² = 10
⇒ w = √10
Hence, Area of rectangle is,
⇒ l × w
⇒ 2√10 × √10
⇒ 2 × 10
⇒ 20 unit²
Hence, The area of figure is,
⇒ 20 + 6
⇒ 26 units²
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ1
If Billy had 39 sweets he recieves twice as much and ate 25 what does Billy have now
Answers
Answer:
53
Step-by-step explanation:
Answer:
Step-by-step explanation:
he had 39 sweets
then he receive 39*2[twice as much as 39] + 39 [the sweet he had before he got more sweet]
39*2=78+39=117-25[the number of sweet he had taken out of the 117 sweets he had before]
117-25=92
Billy has 92 sweets left
Test the exactness of ODE, if not, use an integrating factor to make exact and then find general solution: (2xy-2y^2 e^3x)dx + (x^2 - 2 ye^2x)dy = 0.
Answers
It is requred to test the exactness of the given ODE and then find its general solution. Then, if the given ODE is not exact, an integrating factor must be used to make it exact.
This given ODE is:(2xy - 2y²e^(3x))dx + (x² - 2ye^(2x))dy = 0.To verify the exactness of the given ODE, we determine whether or not ∂Q/∂x = ∂P/∂y, where P and Q are the coefficients of dx and dy respectively, as follows: P = 2xy - 2y²e^(3x) and Q = x² - 2ye^(2x).Then, we have ∂P/∂y = 2x - 4ye^(3x) and ∂Q/∂x = 2x - 4ye^(2x).Thus, since ∂Q/∂x = ∂P/∂y, the given ODE is exact.To solve the given ODE, we have to find a function F(x,y) that satisfies the equation Mdx + Ndy = 0, where M and N are the coefficients of dx and dy respectively. This is accomplished by integrating both P and Q with respect to their respective variables. We have:∫Pdx = ∫(2xy - 2y²e^(3x))dx = x²y - y²e^(3x) + g(y), where g(y) is a function of y. We differentiate both sides of this equation with respect to y, set it equal to Q, and then solve for g(y). We have:(d/dy)(x²y - y²e^(3x) + g(y)) = x² - 2ye^(2x)Thus, g'(y) = 0 and g(y) = C, where C is a constant.Substituting the value of g(y) in the equation above, we get:x²y - y²e^(3x) + C = 0, as the general solution.The given ODE is exact, so we can solve it by finding a function that satisfies the equation Mdx + Ndy = 0. After integrating both P and Q with respect to their respective variables, we find that the general solution of the given ODE is x²y - y²e^(3x) + C = 0.
To know more about integrating factor visit:
brainly.com/question/32554742
#SPJ11
A box of 24 ornaments contains 3/4 red ornaments. How many red ornaments are in the box? How many ornaments are another color than red?
Answers
Answer:
18 red and 6 other color
Step-by-step explanation:
A box of 24 ornaments contains 3/4 red ornaments. How many red ornaments are in the box? How many ornaments are another color than red?
3/4 × 24 = red ornaments
= 18 red
24 - 18 = 6 other color
Charlie bought a skateboard for $97.92. This is 3 times as much as the cost of the helmet he bought. What is the cost of the helmet?
Answers
Answer:
$32.64
Step-by-step explanation:
The computation of the helmet is shown below:
Since the skateboard is purchased for $97.92
And, this is 3 times as the cost of the helmet he purchased
So, the cost of the helmet is
= $97.92 ÷ 3
= $32.64
A coffee shop sells a coffee refill mug for $6.75. Each refill costs $1.25. Last month Kim spent $31.75 on a mug and refills. Write an equation you can use to find the number of refills Kim bought. How many refills did Kim buy?
Answers
Answer:
equation: x(1.25) + 6.75 = 31.75 refills: 20
Step-by-step explanation:
The mug costs $6.75, and you aren't buying multiple cups, so that number stays the same. The number of refills is "x" since we do not know the amount. Next to "x" we multiply 1.25 for the cost of each refill. So now we have "x(1.25)" then we add $6.75 to the equation, for the mug price. Along with the total at the end. To which we now have "x(1.25) + 6.75 = 31.75"
Now we solve the equation. First, subtract 6.75 from each side
x(1.25) + 6.25 = 31.75
-6.25 -6.25
Now we have "x(1.25) = 25" So we have to divide each side by 1.25
x(1.25/1.25) = 25/1.25
x = 20
Therefore, Kim bought 20 refills. To check our work we can replace x with 20 in the original equation.
20(1.25) + 6.75 = 31.75
25 + 6.75 = 31.75
31.75 = 31.75
I'm not the best at explanations, but I hope this helped! :)
The list price of a new printer is $8,000. The chain discount is 20/15/10. What's the net price?
A. $3,204
B. $3,304
C. $4,103
D. $4,896
Answers
The limit below represents a derivative f′(a). Find f(x) and a.
limh→0(5+h)2−25h
f(x)=
a=
Answers
The function f(x) is given by (x + 5)² , and the derivative f'(a) is evaluated at a = -5.
To find f(x) and a, we need to simplify the given limit expression and identify the function and the value at which the derivative is taken.
Expanding the expression (5 + h)² - 25h, we get:
(25 + 10h + h² ) - 25h
25 + 10h + h² - 25h
h² - 15h + 25
Now, we can recognize this expression as the square of the binomial (h - 5)² .
Therefore, f(x) = (x + 5)v, where x represents the variable in the function.
To determine a, we consider the limit expression again, which tends to zero as h approaches 0. This indicates that the derivative is evaluated at a point where the function is defined. Since the expression (x + 5)² represents the square of a binomial, it is symmetric around x = -5. Hence, a = -5.
In summary, the function f(x) is given by (x + 5)² , and the derivative f'(a) is evaluated at a = -5.
Learn more about derivative
brainly.com/question/32963989
#SPJ11
James has 27 metres of red wire and 12 metres
of black wire. He needs to cut both wires into
smaller pieces so that all of the smaller pieces are
the same length and there is no wire left over. The
length of each piece must be a whole number of
metres.
What is the longest he can make each smaller
piece of wire? Give your answer in metres (m).
Answers
Answer:
3m
Step-by-step explanation:
red wire = 27
black wire= 12
so, we take HCF (highest common factor)
which would be 3 so all the wires would be cut into 3m long.
I hope it helps.
Answer:2m
Step-by-step explanation:
as the factors of 12 are:1, 2, 3, 4, 6 and 12
and the factors of 26 are:1, 2, 13 and 26
so if you are talking meters 2 would be the longest
i hope you get this right x
Need this in C. Provided is a sample output for the function needed below. Just need it to add two vectors magnitude and direction and output calculated magnitude and direction- add The add command will be followed by a set of 4 integers. They are pairs of magnitudes and directions for two vectors. This command will compute the magnitudes and directions for resultant vector. Tabs separate the integers. The line will have the format: add −3.60699
−21.82220
22.11829
260.61445
Answers
The `M_PI` constant is used from the `math.h` library to convert between degrees and radians. The `%lf` format specifier is used with `scanf` to read double precision floating-point values.
To calculate the magnitude and direction of the resultant vector obtained by adding two vectors, you can use the following C code:
```c
#include <stdio.h>
#include <math.h>
void add_vectors(double mag1, double dir1, double mag2, double dir2, double *res_mag, double *res_dir) {
double x1 = mag1 * cos(dir1 * M_PI / 180.0); // Convert degrees to radians
double y1 = mag1 * sin(dir1 * M_PI / 180.0);
double x2 = mag2 * cos(dir2 * M_PI / 180.0);
double y2 = mag2 * sin(dir2 * M_PI / 180.0);
double res_x = x1 + x2;
double res_y = y1 + y2;
*res_mag = sqrt(res_x * res_x + res_y * res_y); // Calculate magnitude using Pythagorean theorem
*res_dir = atan2(res_y, res_x) * 180.0 / M_PI; // Convert radians to degrees
}
int main() {
double mag1, dir1, mag2, dir2, res_mag, res_dir;
printf("Enter the magnitude and direction of the first vector (separated by a space): ");
scanf("%lf %lf", &mag1, &dir1);
printf("Enter the magnitude and direction of the second vector (separated by a space): ");
scanf("%lf %lf", &mag2, &dir2);
add_vectors(mag1, dir1, mag2, dir2, &res_mag, &res_dir);
printf("The magnitude of the resultant vector is %.5f\n", res_mag);
printf("The direction of the resultant vector is %.5f\n", res_dir);
return 0;
}
```
This code defines a function `add_vectors` that takes the magnitudes and directions of two vectors as input, and calculates the magnitude and direction of the resultant vector. It then uses the `scanf` function to read the inputs from the user, calls the `add_vectors` function, and finally prints the calculated magnitude and direction of the resultant vector.
The `add_vectors` function performs vector addition by converting the magnitudes and directions into Cartesian coordinates. It then adds the corresponding components, calculates the magnitude using the Pythagorean theorem, and determines the direction using the `atan2` function. The results are stored in the variables pointed to by `res_mag` and `res_dir`.
Note that the `M_PI` constant is used from the `math.h` library to convert between degrees and radians. The `%lf` format specifier is used with `scanf` to read double precision floating-point values.
Learn more about radians here
https://brainly.com/question/30984313
#SPJ11
I need help with this please

Answers
Answer:
you can notice patterns and start to form your own opinions or conclusions.