It takes a turtle 3 hours to walk 1/2 miles. How many hours does it take to walk 6 mile?
Answers
Related Questions
A sequence can be generated by using an= 3an-1, where a1 = 10 and n is a whole number greater than 1.
What are the first 3 terms in the sequence?
A. 3, 13, 23
B. 10, 30, 90
C. 10, 13, 16
D. 3, 30, 300

Answers
Answer:
B
Step-by-step explanation:
using the recursive rule \(a_{n}\) = 3\(a_{n-1}\) and a₁ = 10, then
a₁ = 10
a₂ = 3a₁ = 3 × 10 = 30
a₃ = 3a₂ = 3 × 30 = 90
the first 3 terms are 10 , 30 , 90
The following probability distributions of job satisfaction scores for a sample of information systems (IS) senior executives and middle managers range from a low of 1 (very dissatisfied) to a high of 5 (very satisfied).
Job Satisfaction Score Probability
IS Senior Executives IS Middle Managers
1 0.06 0.04
2 0.09 0.10
3 0.03 0.13
4 0.42 0.45
5 0.40 0.28
(a) What is the expected value of the job satisfaction score for senior executives?
(b) What is the expected value of the job satisfaction score for middle managers (to 2 decimals)?
Answers
Answer:
a) The expected value of the job satisfaction score for senior executives is:
= 4.01
b) The expected value of the job satisfaction score for middle managers is:
= 3.83
Step-by-step explanation:
a) Data and Calculations:
Job Satisfaction Probability
Score
IS Senior Executives IS Middle Managers
1 0.06 0.04
2 0.09 0.10
3 0.03 0.13
4 0.42 0.45
5 0.40 0.28
Low of 1 = very dissatisfied
High of 5 = very satisfied
Job Satisfaction IS Senior Executives IS Middle Managers
Score Probability Expected Value Probability Expected Value
1 0.06 0.06 (1 * 0.06) 0.04 0.04 (1 * 0.04)
2 0.09 0.18 (2 * 0.09) 0.10 0.20 (2 * 0.10)
3 0.03 0.09 (3 * 0.03) 0.13 0.39 (3 * 0.13)
4 0.42 1.68 (4 * 0.42) 0.45 1.80 (4 * 0.45)
5 0.40 2 (5 * 0.40) 0.28 1.40 (5 * 0.28)
Expected value 4.01 3.83
6. Error Analysis Dakota said the third term of the expansion of (2g + 3h) is 36g2h². Explain Dakota's error. Then correct the error.
Answers
The binomial expansion is solved and the error in Dakota's statement is the incorrect substitution of 36g^2h^2 for the correct expression
Given data ,
Dakota made a mistake because the third term of the expansion of (2g + 3h) should have been 36g2h2. The binomial theorem asserts that the expansion of (2g + 3h) is as follows:
( x + y )ⁿ = ⁿCₐ ( x )ⁿ⁻ᵃ ( y )ᵃ
Here, x = 2g and y = 3h. Since term numbers begin at 0, since we are seeking for the third term, r = 2.
So , on simplifying the equation , we get
= nC2 * (2g)⁽ⁿ⁻²⁾ * (3h)²
= (n! / (2! * (n - 2)!)) * (2g)⁽ⁿ⁻²⁾ * (3h)²
= ((n * (n - 1)) / 2) * (2g)⁽ⁿ⁻²⁾ * (3h)²
Hence , the correct expression for the third term of the expansion of (2g + 3h) is ((n * (n - 1)) / 2) * (2g)^(n - 2) * (3h)², where n is the exponent in the binomial expansion.
To learn more about binomial expansion click :
https://brainly.com/question/3537167
#SPJ1
Graph represents the solution set y>5/-2x+2?
Answers
The graph of the linear inequality y > 5 / (-2x + 2) shows a solution of (0, 2.5)
Graph of Linear InequalityThe graph of an inequality in two variables is the set of points that represents all solutions to the inequality. A linear inequality divides the coordinate plane into two halves by a boundary line where one half represents the solutions of the inequality. The boundary line is dashed for > and < and solid for ≤ and ≥.
In the given inequality, y > 5 / (-2x + 2) can be represented on a graph using a graphing calculator.
Kindly find the attached graph below
Learn more on graph of linear inequality here;
https://brainly.com/question/23093488
#SPJ1

The point P=(1/2,y)lies on the unit circle shown below. What is the value of y in simplest form?
Answers
The value of y in simplest form for the point P = (1/2, y) lying on the unit circle is y = ± √(3)/2.
To find the value of y in simplest form for the point P = (1/2, y) lying on the unit circle, we can use the equation of the unit circle, which states that for any point (x, y) on the unit circle, the following equation holds: x^2 + y^2 = 1.
Plugging in the coordinates of the point P = (1/2, y), we get:
(1/2)^2 + y^2 = 1
1/4 + y^2 = 1
y^2 = 1 - 1/4
y^2 = 3/4.
To simplify y^2 = 3/4, we take the square root of both sides:y = ± √(3/4).
Now, we need to simplify √(3/4). Since 3 and 4 share a common factor of 1, we can simplify further: y = ± √(3/4) = ± √(3)/√(4) = ± √(3)/2.
for more search question point
https://brainly.com/question/28162977
#SPJ8
Find the unknown coordinate so the line through the
points has the given slope

Answers
Answer:
#1 (0,-4)
#2 (5,0)
#3 (3,1)
Step-by-step explanation:
#1. (-3, 2) (0, y) slope = -2
slope = rise/run therefore slope = -2/1 or down 2 and over 1
so from -3 to 0 you are going over 3 units (or 3 times) Therefore to find y at x=0, you have to move three steps, or 3 times -2 = -6 so 2-6 = -4
so y intercept (b) = -4 0r (0,-4)
#2 (-7,-4) (x,0) slope (m) = 1/3 -7+12=5 x=5
#3 (4,-3) (x, 1) slope (m) = -4 (4/-1) Moving one unit in slope means
-3=4=1 for Y and 4-1=3 for X therefore the point is (3, 1)
PLS NEED HELP
Participants in a survey were asked the number of hours of television they watch each week. The dot plot shows the distribution of their responses. After the data was recorded in the dot plot, another response was found for a participant who watches 30 hours of television each week.
How will this additional data point affect the mean number of hours of television watched each week?
A. The mean number of hours will remain the same.
B. The mean number of hours will increase.
C. The effect on the mean number of hours cannot be determined.
D. The mean number of hours will decrease.
Answers
Answer:
The mean number of hours will increase.
Step-by-step explanation:
The mean is the sum of all the values in a data set divided by the number of values in that data set.
First, find the mean of the original data set without the additional value. There are 22 values.
So, the mean of the original data set is approximately 7.27 hours.
Next, add the additional data point to the sum of the number of hours, and divide by the new number of values in the data set, 23, to find the new mean.
So, the mean of the data set with the additional value is approximately 8.26 hours.
Since 8.26 > 7.27, the effect of the additional value is that the mean number of hours will increase.
please help guys asap
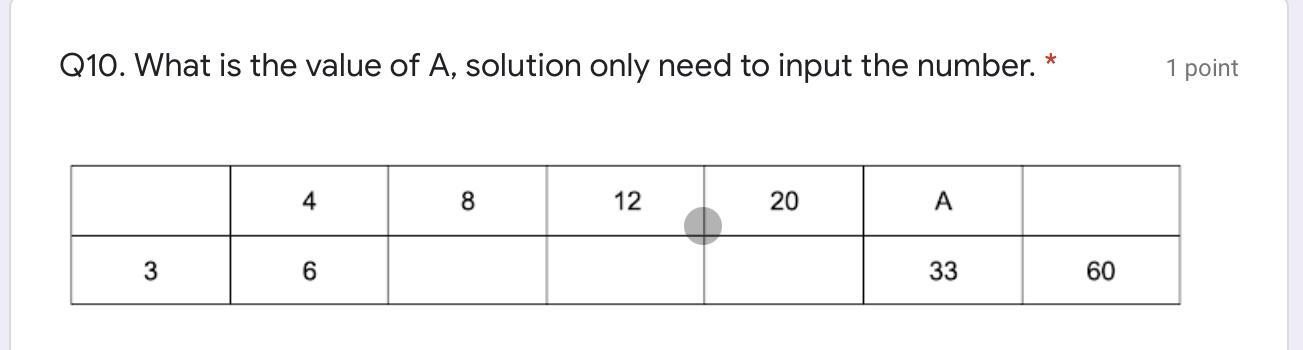
Answers
Answer:
28 i think
Step-by-step explanation:
Suppose a baker claims that the average bread height is more than 15cm. Several of this customers do not believe him. To persuade his customers that he is right, the baker decides to do a hypothesis test. He bakes 10 loaves of bread. The mean height of the sample loaves is 17 cm with a sample standard deviation of 1.9 cm. The heights of all bread loaves are assumed to be normally distributed. The baker is now interested in obtaining a 95% confidence interval for the true mean height of his loaves. What is the lower bound to this confidence interval? 2 cm (round to 2 decimal places) What is the upper bound to this confidence interval? cm (round to 2 decimal places) For the following situations, use RStudio to find the appropriate t-critical values that would be needed to construct a confidence interval. Round all critical values to the second decimal place. 1. n = 15, confidence level is 95%, x= 35 and s = 2.7, t-critical value- 2, n = 37, confidence level is 99%, x= 82 and s = 5.9 t-critical value- 2 3, n 1009, confidence level is 90%, x 0.9 and s-0.04 t- critical value = 2 2
Answers
The correct answer is Confidence interval lower bound: 32.52 cm,Confidence interval upper bound: 37.48 cm
To calculate the confidence interval for the true mean height of the loaves, we can use the t-distribution. Given that the sample size is small (n = 10) and the population standard deviation is unknown, the t-distribution is appropriate for constructing the confidence interval.
The formula for a confidence interval for the population mean (μ) is:
Confidence Interval = sample mean ± (t-critical value) * (sample standard deviation / sqrt(sample size))
For the first situation:
n = 15
Confidence level is 95% (which corresponds to an alpha level of 0.05)
x = 35 (sample mean)
s = 2.7 (sample standard deviation)
Using RStudio or a t-table, we can find the t-critical value. The degrees of freedom for this scenario is (n - 1) = (15 - 1) = 14.
The t-critical value at a 95% confidence level with 14 degrees of freedom is approximately 2.145.
Plugging the values into the formula:
Confidence Interval = 35 ± (2.145) * (2.7 / sqrt(15))
Calculating the confidence interval:
Lower Bound = 35 - (2.145) * (2.7 / sqrt(15)) ≈ 32.52 (rounded to 2 decimal places)
Upper Bound = 35 + (2.145) * (2.7 / sqrt(15)) ≈ 37.48 (rounded to 2 decimal places)
Therefore, the lower bound of the confidence interval is approximately 32.52 cm, and the upper bound is approximately 37.48 cm.
For the second situation:
n = 37
Confidence level is 99% (which corresponds to an alpha level of 0.01)
x = 82 (sample mean)
s = 5.9 (sample standard deviation)
The degrees of freedom for this scenario is (n - 1) = (37 - 1) = 36.
The t-critical value at a 99% confidence level with 36 degrees of freedom is approximately 2.711.
Plugging the values into the formula:
Confidence Interval = 82 ± (2.711) * (5.9 / sqrt(37))
Calculating the confidence interval:
Lower Bound = 82 - (2.711) * (5.9 / sqrt(37)) ≈ 78.20 (rounded to 2 decimal places)
Upper Bound = 82 + (2.711) * (5.9 / sqrt(37)) ≈ 85.80 (rounded to 2 decimal places)
Therefore, the lower bound of the confidence interval is approximately 78.20 cm, and the upper bound is approximately 85.80 cm.
For the third situation:
n = 1009
Confidence level is 90% (which corresponds to an alpha level of 0.10)
x = 0.9 (sample mean)
s = 0.04 (sample standard deviation)
The degrees of freedom for this scenario is (n - 1) = (1009 - 1) = 1008.
The t-critical value at a 90% confidence level with 1008 degrees of freedom is approximately 1.645.
Plugging the values into the formula:
Confidence Interval = 0.9 ± (1.645) * (0.04 / sqrt(1009))
Learn more about Confidence interval here:
https://brainly.com/question/15712887
#SPJ8
Answer the question in the picture.

Answers
Answer: J = 33
Step-by-step explanation:
the corner of the triangle is 90 degrees so
90 + 57 = 147
Now the rest is 33 degrees.
Since it'll equal to 180 degrees.
Answer:
It's 33 degree
explanation:
Two triangles are similar so
angle K is equal angleQ=90DEGREE
ANGLE J=AngleP=33
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment

i need help with this problem

Answers
Step-by-step explanation:
Pythagoras theorem
16²=7²+a²
a²=16²-7²
a²= 256 -49
a²=207
a=√207
a=14.38
a≈14.4 in. (approx)
Answer:
Step-by-step explanation:
As it is a right angle triangle, we can use Pythagorean theorem to find a
base² + altitude² = hypotenuse²
7² + a² = 16²
49 + a² = 256
a² = 256 - 49
a² = 207
a = √207
a = 14.4 in
Help me out here pleaseeeeeeeeee

Answers
find the equation of the line passing through the point (4,-2) and parallel to the line 6y=7x-5
Answers
Answer: 6y = 7x - 40
Step-by-step explanation:
Create a variable h that is a row vector with eight equally spaced elements in which the first element is 68 and the last element is 12.
Answers
The variable h, which is a row vector with eight equally spaced elements, is h = linspace(68, 12, 8).
To create the variable h as a row vector with eight equally spaced elements, we can use the linspace function in MATLAB or Octave. The linspace function takes three arguments: the starting value, the ending value, and the number of elements in the vector.
Here's how to create the variable h with the desired specifications:
h = linspace(68, 12, 8)This will create a row vector h with eight equally spaced elements ranging from 68 to 12. The output will be:
h = [68 60.5 53 45.5 38 30.5 23 12]The elements in the vector are not integers because we asked for eight equally spaced elements between 68 and 12.
Learn more about MATLAB code brainly.com/question/15071644
#SPJ4

Differentiate y=x4 -x
Answers
Answer:
Step-by-step explanation:
To differentiate the function y = x^4 - x, we will use the power rule of differentiation. The power rule states that if f(x) = x^n, then the derivative of f(x) is f'(x) = nx^(n-1).
So, for y = x^4 - x, we can find the derivative as follows:
y' = 4x^3 - 1
So, the derivative of the function y = x^4 - x is y' = 4x^3 - 1.
need help plz help me out i have a bad grade rn

Answers
Answer:
I only know the second part sorry
9.35
Step-by-step explanation:
3(9)÷4+2.6=
27÷4+2.6=
6.75+2.6=
9.35
What is the approximate area of the shaded sector in the circle shown below
A. 283 cm
B. 31.4cm2
C. 565cm2
D. 15.7 cm2

Answers
Answer:
Option A. 283 cm²
Step-by-step explanation:
to find the area of the shaded sector, we use the formula:
\(\frac{\text{angle given}}{360^\circ}\times \text{area of the circle}\)
where area of the circle = πr²
∴ for the given circle,
\(\text{Area of the sector}=\frac{\text{given angle}}{360^\circ} \times \pi r^2\)
= \(\frac{100}{360}\times 3.14\times 18\times 18\)
= \(\frac{100}{360}\times 1017.36\)
= 282.6
≈ 283 cm²
The approximate area of the shaded sector is 283 cm².
I need help with number 7.

Answers
Answer:
A) 41%
Step-by-step explanation:
the complement of at least one balloon being hit is no balloons being hit
thus, if "at least one balloon is hit" is false, "no balloons are hit" is true
1 - probability something is false = probability it is true
1 - probability no balloons are hit = probability at least one balloon is hit
probability no balloons are hit = P(A and B and C and D and E), where each event is a balloon is not hit
probability a balloon is hit = 1/10 = 0.1
probability a ballon is not hit = 1 - probability a balloon is hit = 1-0.1 = 0.9
P(A and B) = P(A) * P(B)
P(A and B and C and D and E) = 0.9*0.9*0.9*0.9*0.9 = 0.9^5 = 0.59049 = probability no balloons are hit
1 - probability no balloons are hit = probability at least one balloon is hit = 1-0.59049 = 0.40951 ≈41%
If a punch bottle says 10% fruit juice, and it is a 150 milliliter bottle, how many milliliters of fruit juice is in the bottle?
Answers
Answer:
i believe the answer is 15 milliliters
Step-by-step explanation:
Answer:
Figure it out yourself
Step-by-step explanation:
Please help me with this

Answers
The volume of rectangular prism is 90 unit³.
We can consider the 1 block = 1 unit.
Length of prism = 5 unit
width of prism = 6 unit
Height of prism = 3 unit
So, Volume of rectangular prism
= l w h
= 5 x 6 x 3
= 90 unit³
Thus, the volume of rectangular prism is 90 unit³.
Learn more about Volume here:
https://brainly.com/question/1578538
#SPJ1
Which expression correctly represents "six more than the quotient of three and a number, decreased by eight"?
6+3/n-8
6+n/3-8
6+3/n+8
6+n/3+8
Answers
The option A is correct because the value of the statement is 6+3/n-8.
According to the statement
we have given that the statement and we have to write the statement in the numerical form.
So, For this purpose
we know that the given statement is
"Six more than the quotient of three and a number, decreased by eight".
In this statement "Six more than" indicates the sum between the quotient and 6.
And "The quotient of three and a number" indicates a fraction where the numerator is 3 and the denominator is , a number.
"Decreased by eight" indicates a subtraction between the quotient an 8 units".
If we unit all parts of the statements, we would have
6+3/n-8
So, From the given statement, The option A is correct because the value of the statement is 6+3/n-8.
Learn more about Numbers here
https://brainly.com/question/11408596
#SPJ1
Need help in Qa, Qc, Qe and Qf.
With workings for each of the following please, Thank you!!

Answers
The expression in the form (x +a)² + b is shown below.
We have to expression given expression in the form (x +a)² + b.
1. x² + 12x
x² + 12x + 36 - 36
= (x +6)² - 36
2. x² + 3x - 2
x² + 2 . 3x /2 - 9/4 + 9/4 -2
(x+ 3/2)² - 17/4
3. x²+ 1/2 x
x² + 2 . 1/4 x + (1/2)² - (1/2)²
= (x+ 1/2)² - 1/4
4. x² - 2/9 x
= x² + 2 . 2/20 x + 4/400 - 4/400
= (x+ 2/200)² - 1/100
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ1
Find the perimeter of the figure shown above with aside length 5 unit

Answers
The perimeter of the figure with side length of 5 units is 50 units
How to determine the perimeter of the figureFrom the question, we have the following parameters that can be used in our computation:
Shape = rectangle
Smaller shapes = squares
Side lengths = 5 units
The perimeter of the figure is calculated as
Perimeter = Number of visible sides * Side length of the square shape
In this case, we have
Number of visible sides = 10
Substitute the known values in the above equation, so, we have the following representation
Perimeter = 10 * 5
Evaluate the products
Perimeter = 50 units
Hence, the perimeter is 50 units
Read more about perimeter at
https://brainly.com/question/18019422
#SPJ1
Part A
There were 600 water samples taken for an experiment using pH and iron levels. The results are shown in the table.
What are the probabilities for the listed events? Write your answers as decimals rounded to the thousandths place.

Answers
Answer:
The answer to your problem is, 0.275 0.273 0.400 and 0.300
Step-by-step explanation:
My calculation ( May not be correct )
P ( low iron or LI ) \(\frac{165}{600}\) = 0.275
P ( low pH | LI ) = \(\frac{45}{165}\) = 0.273
P ( low pH ) = \(\frac{150}{600}\) = 0.400
P ( LI | Low pH ) = \(\frac{45}{150}\) = 0.300
Thus by making these calculations the answer to your problem is, 0.275 0.273 0.400 and 0.300
Find the coordinate of each play under the given dilation(-2, 4); skill factor of 2, center of dilation at the origin

Answers
The origin is often used as the center of dilation. If you are dilating a figure centered at the origin, you can multiply the coordinates of the points in the preimage by the scale factor to determine the points in the image.
Given a scale factor of k, the transformation is given by
\((x,y)\rightarrow(kx,ky)\)On our problem, we want to perform a dilation at (-2, 4) with a scale factor of 2, therefore, we have
\((-2,4)\rightarrow(-2\cdot2,4\cdot2)=(-4,8)\)After the dilation the coordinates are (-4, 8).
help pls A rational expression has been simplified below.
(x-2)(x+6)/7(x+6) = x-2/7
For what values of x are the two expressions equal?
O A. All real numbers except 2
OB. All real numbers
O C. All real numbers except -6
O D. All real numbers except -6 and 2

Answers
All real numbers, with the exception of -6 , are the solution to a rational equation. The quotient of two polynomials is the definition of a rational expression.
What do you meant by rational expression ?\($\frac{(x-2)(x+6)}{7(x+6)}=\frac{x-2}{7} \quad: \quad x \neq-6$\)
\($\frac{(x-2)(x+6)}{7(x+6)}=\frac{x-2}{7}$\)
Simplify
\($\frac{(x-2)(x+6)}{7(x+6)}: \quad \frac{x-2}{7}$\)
\($\frac{x-2}{7}=\frac{x-2}{7}$\)
Seven times both sides
\($\frac{x-2}{7} \cdot 7=\frac{x-2}{7} \cdot 7$\)
Simplify
\($x-2=x-2$\)
There is equality between the two sides.
For every x Verify Solutions, true
Search for ill-defined (singularity) points: \($x=-6$\)
Because -6, the equation is undefined.
\(x \neq -6\)
Therefore the correct answer is option C ) All real numbers except -6 .
To learn more about rational expression refer to :
https://brainly.com/question/30291585
#SPJ1
The distance between two towns is 120 kilometers there are approximately 8 kilometers in 5 miles which measurement is closest to the number of mules between these two towns
Answers
Answer:
75 Kilometers
Step-by-step explanation:
We have been given that the distance between two towns is 120 km.
We are also told that there are approximately 8 km in 5 miles. Let us find number of miles per km by dividing 5 by 8.
\text{Number of miles in 1 km}=\frac{5\text{ miles}}{\text{8 Km}}
\text{Number of miles in 1 km}=0.625\frac{\text{ miles}}{\text{ Km}}
Therefore, there are 0.625 miles in 1 km.
To convert our given distance into miles we will multiply our given distance by number of miles in 1 km.
\text{Number of miles in 120 km}=120\text{ km}\times \frac{0.625\text{ miles}}{\text{ km}}
\text{Number of miles in 120 km}=120\times 0.625\text{ miles}
\text{Number of miles in 120 km}=75\text{ miles}
Therefore, the distance between two towns is 75 miles.
Answer:
The answer is 75, I had this question a few days ago and I got it right
Answer:75
3 n - 5 p + 2 n = 10 p for n
Answers
Answer:
What do you mean
Step-by-step explanation:
Please help meeeeeeeeeee
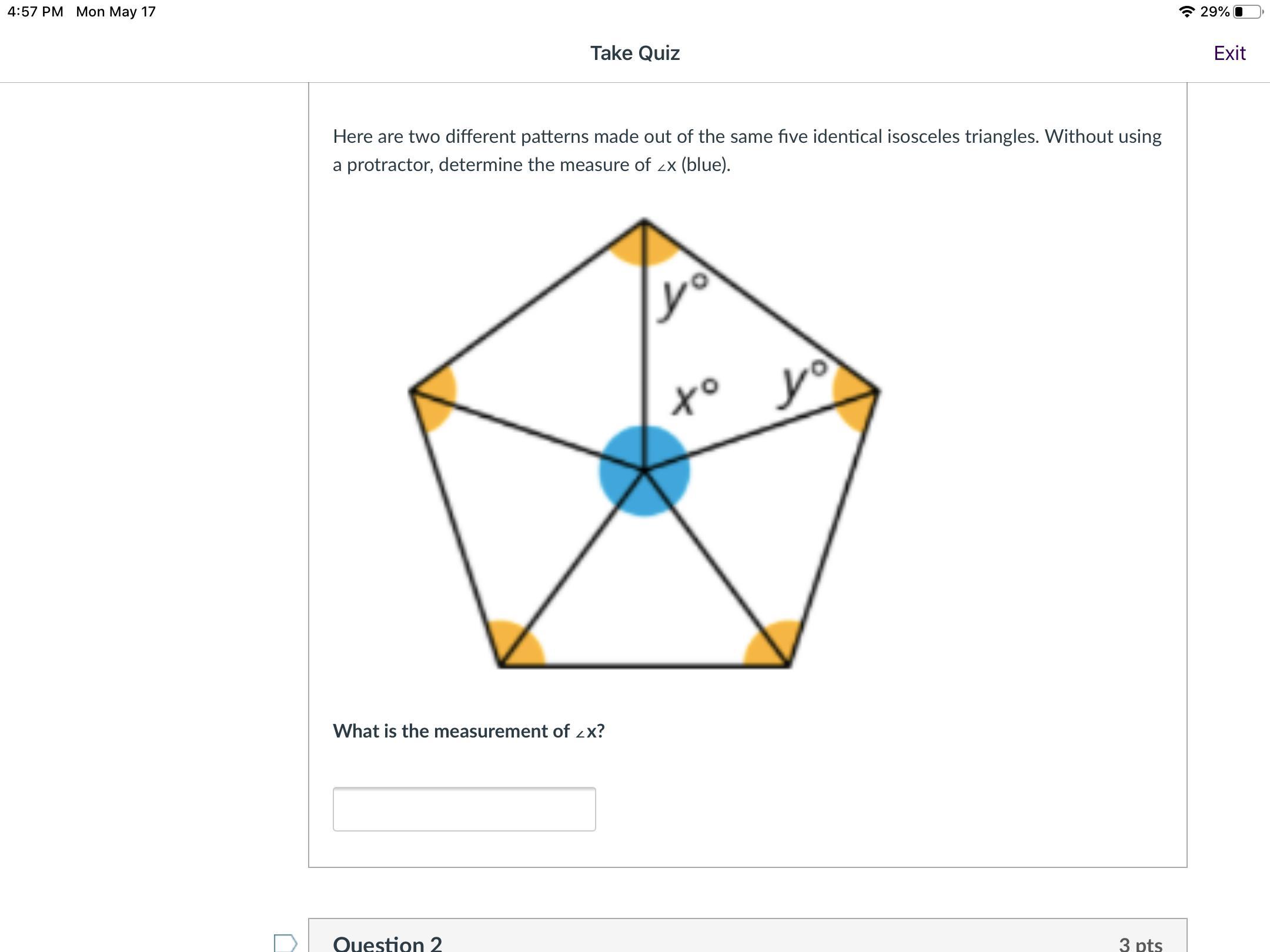

Answers
Answer:
x=72
y=54
Step-by-step explanation:
1st question. y=54 because it is a bisector of the 108 degree angles. (a polygon's interior angles add to number of sides minus 2 times 180)
There are two ys, so they add up to 108. A triangle's interior angles add to 180. 180-108 =72 x=72
2nd question, x is 72 ( it says x is the same measure) so 180-72=2y.
y still equals 54
Answer:
this is so easy
Step-by-step explanation:
3000* (15) (300) divided by 20 x 60 100ft divided by 40