Is this right?
Any links get reported!

Answer: A = P + 0.2P

Step-by-step explanation:

r = 0.04, t = 5

Original equation:

A = P + Prt

A = P + P(0.04)(5)

A = P + P(0.2)

Answer: the slope is 1

Step-by-step explanation:

1. Let B={4}. Note that B⊂A. Find a subset C of A such that B∪C=A and B∩C=∅.Subset C of A can be calculated as follows: C = A - B = {2, 3, 6, 9}2. Let D={3,9}. Note that D⊂A. Find a subset E of A such that D∪E=A and D∩E=∅.Subset E of A can be calculated as follows:E = A - D = {2, 4, 6}3.

How many distinct pairs of disjoint non-empty subsets of A are there, the union of which is all of A?The set A contains 5 elements; hence it has 2^5-1 = 31 non-empty subsets. A set of two non-empty subsets of A is disjoint if and only if one of them does not contain an element that is present in the other.

If the first subset has k elements, the number of such disjoint pairs is equal to the number of subsets of the remaining 5-k elements which is 2^(5-k)-1. Hence the total number of disjoint pairs of non-empty subsets of A is equal to 2^5-1 + 2^4-1 + 2^3-1 + 2^2-1 + 2^1-1 = 63.There are 63 distinct pairs of disjoint non-empty subsets of A that have the union as all of A.

To know more about disjoint visit :

https://brainly.com/question/29272324

#SPJ11

The result of the two-sided test with the null hypothesis of the population mean equaling 43, based on the 95% confidence interval that ranges from 35 to 45, would be rejecting the null hypothesis.

The 95% confidence interval that ranges from 35 to 45 suggests that we are 95% confident that the true population mean falls between those values.

To conduct a two-sided test with the null hypothesis of the population mean equaling 43, we can use the confidence interval to see if the null hypothesis falls within the range of the confidence interval or not.

Since the null hypothesis of 43 is not within the confidence interval of 35 to 45, we can reject the null hypothesis at the 0.05 level of significance, which means we have evidence to suggest that the true population mean is not 43.

Therefore, the likely result of our test would be rejecting the null hypothesis.

Learn more about two sided test here

brainly.com/question/16842072

#SPJ4

The possible values of k are k = 2 and k = -2. These are the values of the constant k for which f(x) is continuous at x = 2.

A relation between a collection of inputs and outputs is known as a function. A function is, to put it simply, a relationship between inputs in which each input is connected to precisely one output.

To determine the values of the constant k for which f(x) is continuous at x = 2, we need to ensure that the left-hand limit, the right-hand limit, and the value of f(x) at x = 2 are all equal.

First, let's find the left-hand limit as x approaches 2. We evaluate the function for x < 2:

f(x) = x² + 5kx    (for x < 2)

Taking the limit as x approaches 2 from the left side (x < 2), we have:

lim(x→2-) f(x) = lim(x→2-) (x² + 5kx) = 2² + 5k(2) = 4 + 10k

Next, let's find the right-hand limit as x approaches 2. We evaluate the function for x > 2:

f(x) = k²x + 4x + 4    (for x > 2)

Taking the limit as x approaches 2 from the right side (x > 2), we have:

lim(x→2+) f(x) = lim(x→2+) (k²x + 4x + 4) = k²(2) + 4(2) + 4 = 2k² + 8 + 4 = 2k² + 12

Now, let's evaluate the value of f(x) at x = 2:

f(x) = 3k² - 4    (for x = 2)

f(2) = 3k² - 4

For f(x) to be continuous at x = 2, the left-hand limit, the right-hand limit, and the value of f(x) at x = 2 should all be equal. Therefore, we set up the following equation:

4 + 10k = 2k² + 12 = 3k² - 4

Simplifying, we have:

2k² + 8 = 3k² - 4

Rearranging the terms, we get:

k² - 12 = 0

Factoring, we have:

(k - 2)(k + 2) = 0

So, the possible values of k are k = 2 and k = -2. These are the values of the constant k for which f(x) is continuous at x = 2.

Learn more about function on:

https://brainly.com/question/11624077

#SPJ4

Polynomials are  closed under the operations of addition, subtraction, and multiplication, polynomials constitute a system similar to that of integers.

Polynomial exponents are whole numbers.

The fact that addition is closed for the whole numbers ensures that the resultant exponents will also be whole numbers. Polynomials are hence closed under addition.

Polynomials will be closed under an operation if the operation produces another polynomial.

If we subtract 2 polynomials, the result is a polynomial. Therefore, they are also closed under subtraction.

Polynomials are an algebraic equation that has more than two terms, particularly the accumulation of numerous phrases that each include a different power of the same variable (s).

To learn more about polynomials and closure property

https://brainly.com/question/27287760

#SPJ4

The probability of selecting the chicken, cow, and human is (1/97) * (1/47) * (1/77).

When randomly selecting one creature from the sample of 97 chickens, 47 cows, and 77 humans, each creature has an equal probability of being selected. Therefore, the probability of selecting the chicken is 1 out of 97 (1/97), the probability of selecting the cow is 1 out of 47 (1/47), and the probability of selecting the human is 1 out of 77 (1/77).

To find the probability of all three events happening together (selecting the chicken, cow, and human in that order), we multiply the individual probabilities. This is because the events are independent, meaning the selection of one creature does not affect the probabilities of selecting the others.

Multiplying the probabilities, we have:

(1/97) * (1/47) * (1/77) ≈ 0.000000000274

Therefore, the probability of selecting the chicken, cow, and human is approximately 0.000000000274.

Learn more about: Probability

brainly.com/question/31828911

#SPJ11

Answer:

Step-by-step explanation:

∠K = 180 - 67.8

    = 112.2°

∠J = ∠L = 180 - 112.2

                      2

∠J = ∠L = 33.9°

The conditional probability mass functions are: (a) P(X1 = 1|X3 = 1) = 2/9, (b) P(X2 = 1|X3 = 1) = 4/9, (c) P(X1 = 1|X3 = 1) = 4/14, (d) P(X2 = 1|X3 = 1) = 8/14.

(a) The conditional probability mass function given that is:

P(W1=1, W2=k | W3=j) = P(W1=1, W2=k) * P(W3=j | W1=1, W2=k) / P(W3=j)

Using Bayes' Theorem, we have:

P(W1=1, W2=k | W3=j) = (4/14) * (3/13) * (10/12) / [(4/14) * (3/13) * (10/12) + (10/14) * (4/13) * (10/12)]

Simplifying the expression, we get:

P(W1=1, W2=k | W3=j) = 6/23 if j is black and k is white, 5/46 if j is white and k is black, and 5/69 if j and k are both white.

(b) The conditional probability mass function given that is:

P(W1=k, W2=j | W3=1) = P(W1=k, W2=j) * P(W3=1 | W1=k, W2=j) / P(W3=1)

Using Bayes' Theorem, we have:

P(W1=k, W2=j | W3=1) = (4/14) * (3/13) * (10/12) / [(4/14) * (3/13) * (10/12) + (10/14) * (4/13) * (10/12)]

Simplifying the expression, we get:

P(W1=k, W2=j | W3=1) = 6/23 if k is black and j is white, 5/46 if k is white and j is black, and 5/69 if k and j are both white.

(c) The conditional probability mass function given that is:

P(W1=1, W2=k | W3=j) = P(W1=1) * P(W2=k) * P(W3=j) / (P(W1=1) * P(W2=k) * P(W3=j))

Since the balls are selected with replacement, the probability of selecting any ball is always the same. Therefore, the conditional probability mass function is the same as the joint probability mass function, which is:

P(W1=1, W2=k | W3=j) = (4/14) * (4/14) * (4/14) = 16/2744 if j, k are both white and 0 otherwise.

(d) The conditional probability mass function given that is:

P(W1=k, W2=j | W3=1) = P(W1=k) * P(W2=j) * P(W3=1) / (P(W1=k) * P(W2=j) * P(W3=1))

Since the balls are selected with replacement, the probability of selecting any ball is always the same. Therefore, the conditional probability mass function is the same as the joint probability mass function, which is:

P(W1=k, W2=j | W3=1) = (4/14) * (4/14) * (10/14) = 80/2744 if k is white and j is black, and 0 otherwise.

To learn more about conditional probability, click here: brainly.com/question/27684587

#SPJ11

If the standard deviation of a set of data is 6, then the value of variance is 36

The formula for determining variance is variance = √Standard deviation

Variance of a set of data is equal to square of the standard deviation.

If the standard deviation of a set of data is 6 then we get variance by putting the value of standard deviation in the formula

variance = √Standard deviation

Take square root on both sides

Standard deviation² = 6²

Standard deviation= 36

Hence,  standard deviation of a set of data is 6, then the value of variance is 36

To learn more on Statistics click:

https://brainly.com/question/30218856

#SPJ1

The value of height of triangle is 12.3 units.

A triangle is a polygon with three sides, three angles, and three vertices (or corners). It is one of the most fundamental shapes in geometry and has many unique properties that make it a useful tool in mathematics and science.

The sum of the three interior angles of a triangle is always 180 degrees, and the length of one side of a triangle is always less than the sum of the lengths of the other two sides.

Given;

Triangle is right angle

hypotenuse=18 units

Using trigonometric formula

sin43=y/18

.68=y/18

y=12.3

Value of height of triangle is 12.3 units.

To know more about polygon, visit:

https://brainly.com/question/24464711

#SPJ1

Answer:

There are $\boxed{3}$ paths from $A$ to $B.$

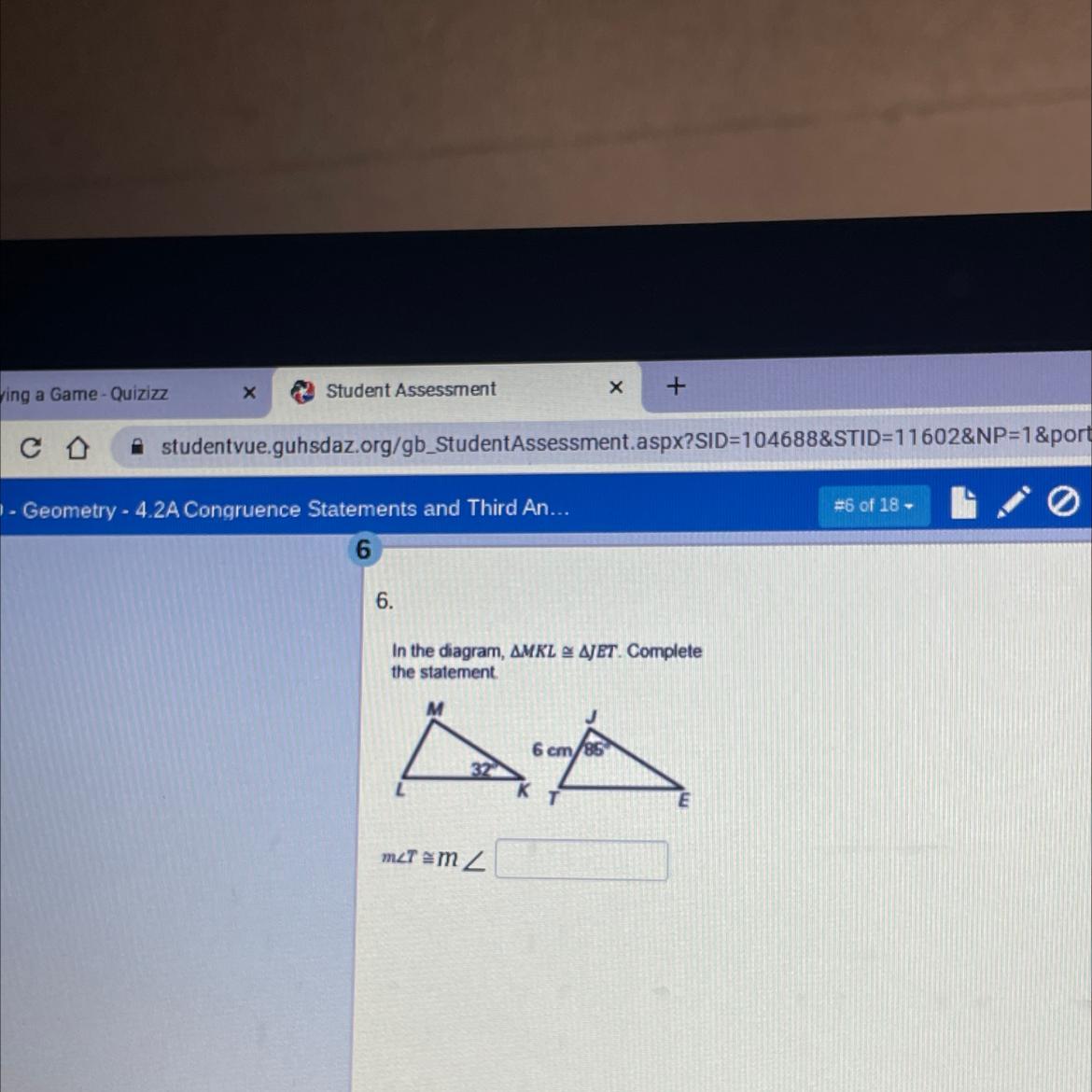
Answer:

See below

Step-by-step explanation:

It's hard to see your photo but if that say m∠T than your answer would be

m∠ L.

The drawings are saying the the triangles are congruent which means all the interior angles of one triangle are congruent to the angles of the second triangle.    m∠M = m∠J,   m∠K = m∠E and m∠L = m∠T

Since you have two of the angles, you can also determine what m∠L and m∠T is equal to.  The sum on all interior angles must be 180 degrees.

180 - 86 - 32 = 62

Answer:

15500 pounds

Step-by-step explanation:

The weight of one load is 4 tons and the weight of other load is 7500 pounds.

We know that, 1 ton = 2000 pounds

4 tons = 8000 pounds

Total weight = 8000 pounds + 7500 pounds

Total weight = 15500 pounds

So, the total weight of sand is 15500 pounds.

Answer:

236.25

Step-by-step explanation:

15.75 sq yards * 15 dollars per sq yards = 236.25

You multiply the amount of square yards with the amount each costs to get your answer.

Hope this helps!

Answer:

Step-by-step explanation:

∠R + ∠S + ∠T = 180 {Angle sum property of triangle}

∠R + 56 + 30  = 180

         ∠R + 86 = 180

               ∠R   = 180 - 86

                ∠R =   94

Numbers that have a proportional relationship are:

So, 0.5 ⇒ 3:

Therefore, numbers that have a proportional relationship are:'

Know more about proportional relationships here:

https://brainly.com/question/3383226

#SPJ9

The value of the 7th term in the sequence 18, 6, 2, ... is 2/81.

It's important to note that this is a geometric progression and the formula will be illustrated as:

= ar^(n - 1)

where a = first term = 18

r = common ratio = 1/3

The value of the 7th term will be calculated thus:

= ar^(n - 1)

= 18 × (1/3)^(7 - 1)

= 18 × 1/3^6

= 18 × 1/729

= 2/81

The term is 2/81.

Learn more about sequence on:

brainly.com/question/7882626

#SPJ1

Answer:

what is the question...............?

Yes, if the mean weight of two groups of children is different with a p-value of 0.03, the difference is statistically significant. Typically, a p-value of less than 0.05 is considered statistically significant, indicating that the observed difference is unlikely to be due to chance alone.

Yes, if the p level is .03, then the difference in mean weight between the two groups of children is statistically significant. The p level that identifies statistical significance is generally considered to be .05 or less, meaning that there is a 5% or less chance that the difference observed is due to random chance rather than a true difference between the two groups. Therefore, a p level of .03 is below the commonly accepted threshold for statistical significance and suggests that the difference in mean weight is not likely due to chance alone.

Know more about p-value here:

https://brainly.com/question/30078820

#SPJ11

The value of particular solution to the nonhomogeneous differential equation is,

⇒ y (p) = 2x + 1/2 e⁻ˣ - 8/5

We have to given that;

The nonhomogeneous differential equation is,

⇒ y'' + 4y' + 5y = 10x + e⁻ˣ  . (i)

To find homogeneous solution,

D² + 4D + 5 = 0

(D + 2)² = - 1

D + 2 = ±i

D = 2 ± i

Hence, We get;

y = e⁻²ˣ (c₁ cos x + c₂ sin x)  .. (ii)

To find the particular solution,

y (p) = A + Bx + Ce⁻ˣ

y' (p) = B - Ce⁻ˣ

y'' (p) = Ce⁻ˣ

Substitute all the values in (i);

⇒ y'' + 4y' + 5y = 10x + e⁻ˣ

⇒ Ce⁻ˣ + 4(B - Ce⁻ˣ) + 5(A + Bx + Ce⁻ˣ) = 10x + e⁻ˣ

Equating the coefficient;

A = 2

B = - 8/5

C = 1/2

So, We get;

⇒ y (p) = 2x + 1/2 e⁻ˣ - 8/5

The value of particular solution to the nonhomogeneous differential equation is,

⇒ y (p) = 2x + 1/2 e⁻ˣ - 8/5

Learn more about the function visit:

https://brainly.com/question/11624077

#SPJ4

The probability of : (a) P(X ≤ 1/2) = 1/4, (b) P(X ≥ 3/4) = 7/16, (c) P(X ≥ 2) = 0, (d) E[X] = 2/3, and SD[X] = 1/√18.

Part (a) : To find P(X ≤ 1/2), we need to integrate the density function from 0 to 1/2:

So, P(X ≤ 1/2) = \(\int\limits^{\frac{1}{2}} _0 {} \,\) 2x dx = x² [0, 1/2] = (1/2)² = 1/4,

Part (b) : 1To find P(X ≥ 3/4), we need to integrate the density function from 3/4 to 1:

P(X ≥ 3/4) = \(\int\limits^1_{\frac{3}{4}}\)2x dx = x² [3/4, 1] = 1 - (3/4)² = 7/16,

Part (c) : To find P(X ≥ 2), we need to integrate the density function from 2 to infinity. But, the density function is zero for x > 1, so P(X ≥ 2) = 0.

Part (d) : The expected-value of X is given by:

E[X] = ∫₀¹ x f(x) dx = ∫₀¹ 2x² dx = 2/3

Part (e) : The variance of X is given by : Var[X] = E[X²] - (E[X])²

To find E[X²], we need to integrate x²f(x) from 0 to 1:

E[X²] = ∫₀¹ x² f(x) dx = ∫₀¹ 2x³ dx = 1/2

So, Var[X] = 1/2 - (2/3)² = 1/18

Next, standard-deviation of "X" is square root of variance:

Therefore, SD[X] = √(1/18) = 1/√18.

Learn more about Standard Deviation here

https://brainly.com/question/30394343

#SPJ4

Answer:

the bottom left one error is on step 3

Step-by-step explanation:

Answer:

poines

Step-by-step explanation:

The value of the integral ∫(i to 0) f(x) dx is -5.

To find the value of the integral, we'll use the properties of definite integrals.

Given that:
∫(i to 1) f(x) dx = -8 (1)
∫(0 to 1) f(x) dx = -3 (2)
We need to find the value of:
∫(i to 0) f(x) dx
Using the properties of definite integrals, we can rewrite the required integral as:
∫(i to 0) f(x) dx = -∫(0 to i) f(x) dx
Now, let's subtract equation (1) from equation (2):
∫(0 to 1) f(x) dx - ∫(i to 1) f(x) dx = -3 - (-8)
This can be simplified as:
∫(0 to i) f(x) dx = 5
Now, we can substitute the value we found into our original equation:
∫(i to 0) f(x) dx = -∫(0 to i) f(x) dx = -5.

For similar question on integral.

https://brainly.com/question/31618662

#SPJ11

Answer:

x=10

Step-by-step explanation:

3(4x-12) = 84

Divide each side by 3

3/3(4x-12) = 84/3

4x-12 =28

Add 12 to each side

4x-12+12 = 28+12

4x= 40

Divide each side by 4

4x/4 = 40/4

x = 10

The respective sides of the two square pyramids are proportionate since they are comparable. Let's use A cm2 to represent the smaller pyramid's surface area.

The square of the ratio of the corresponding side lengths of comparable pyramids is equal to the ratio of their surface areas. As a result, we may construct the equation shown below:

(s_small / s_large) = (A / 2304)²

where the sides of the smaller and larger pyramids, respectively, are represented by the lengths s_small and s_large, respectively.

We are unable to immediately solve for A since we lack the precise side length data. The ratio of the surface areas is still measurable, though:

(s_small / s_large) = (A / 2304)²

Using the information provided, we can determine that the surface area of.

learn more about comparable here :

https://brainly.com/question/31877486

#SPJ11

14÷3= 4.6666666...

so 4 cookies for each one... with 2 cookies left

The person who has the fastest speed is given as follows:

Aubri and Tyler(tied).

A proportional relationship is a type of relationship between two quantities in which they maintain a constant ratio to each other. This means that if one quantity is multiplied by a certain factor, the other quantity will also be multiplied by the same factor.

The equation that defines the proportional relationship is given as follows:

y = kx.

In which k is the constant of proportionality, representing the increase in the output variable y when the constant variable x is increased by one.

The constant for each person, representing the velocity, is given as follows:

The problem asks for the person who has the fastest speed.

More can be learned about proportional relationships at https://brainly.com/question/7723640

#SPJ1