Answers
Answer:
Yes, you are correct.
Step-by-step explanation:
\(\text{Let the number of puzzle solved by Child B is} x\text{.}\)
\(\text{Then the average number of puzzle solved is}\)
\(\frac{5x+x+(x+4)}{3}=13\)
\(\frac{7x+4}{3}=13\)
\(7x+4=39\)
\(7x=35\)
\(x=5\)
\(\text{Therefore, the number of puzzles solved by child A is }5x=5\cdot5=25\)
\(\color{blue}\text{A little tips here: You can check it by substituting your answer to the original equation.}\)
Answer:
You are correct.
Step-by-step explanation:
\(13 \times 3 = 9\)
Child B completed \( x \)
Child A = \(5x\)
Child C = \(x + 4\)
\(x + 5x + x + 4 = 39\)
\(7x = 35\)
\(x = 5\)
Child A = \(5 \times 5 = 25\)
Related Questions
What is 100 - (9 - 3)2
Answers
Answer:
88
Step-by-step explanation:
100 - (9 - 3)2
100 - (6)2 = 100-12 = 88
100- (6)2
100-12
88
Where would you place root 8 on the Venn diagram? A) integers B) natural numbers C) rational numbers D) irrational numbers

Answers
Answer:
Option (D)
Step-by-step explanation:
All rational and irrational numbers are real numbers.
{-2, -1, -1.8, 0, 1, 2.......}
Numbers written in the form of \(\frac{p}{q}\) are rational numbers. They are the part of irrational numbers.
{-2.5, -2, -1, 0, 1, 2.....}
Whole numbers with negative or positive notation are integers.
{-3, -2, -1, 0, 1, 2, 3, 4......}
Positive integers are the whole numbers (including zero).
{0, 1, 2, 3, 4, .......}
All whole numbers excluding zero are the natural numbers.
{1, 2, 3, 4,........}
Irrational numbers are the part of real numbers written in the form of \(\frac{p}{q}\).
{\(\sqrt{2},\sqrt{5},\pi, \sqrt{10}\)}
Therefore, \(\sqrt{8}\) comes under Irrational numbers.
Option (D) is the answer.
If y= -7(-2-2x), what is the value of x when y is equal to 70?
Answers
Substitute 70 in for the y.
70 = -7(-2-2x)
Then multiply everything inside the parenthesis by -7.
70 = 14 + 14x
Then subtract 14 on both sides
56 = 14x
Divide by 14 on both sides
x = 4
Brigid has a 25-foot ladder she will use to paint the side of her house. What angle does the ladder need to make with house so she can reach 18 feet up the side of her house
Answers
The ladder needs to make an angle of approximately 54.7 degrees with the house in order for Brigid to reach 18 feet up the side of the house.
To determine the angle the ladder needs to make with the house, we can use the tangent function.
First, we'll need to determine the opposite side (the height that the ladder needs to reach) and the adjacent side (the distance from the base of the ladder to the house) of the triangle formed by the ladder and the house.
Opposite side = 18 feet
Adjacent side = 25 feet
We can then use the tangent function to find the angle:
tan(angle) = opposite / adjacent
Solving for the angle, we get:
angle = arctan(18/25) = approximately 54.7 degrees
Therefore, the ladder needs to make an angle of approximately 54.7 degrees with the house in order for Brigid to reach 18 feet up the side of the house.
To learn more about the triangle, visit:
brainly.com/question/2773823
#SPJ4
Apply the Empirical RuleA 3-column table has 1 row. The first column is labeled Age with entry 7 years. The second column is labeled Mean with entry 49 inches. The third column is labeled Standard Deviation with entry 2 inches. According to the empirical rule, 68% of 7-year-old children are between inches and inches tall.
Answers
The empirical norm therefore states that 68% of 7-year-old kids are between 47 and 51 inches tall.
What does a table column mean?A column in a table is a collection of cells which are arranged vertically. A field, like the received field, is a sort of element that contains only one item of data. A column in a table usually contains the values for just a single field.
The empirical rule states that in a normal distribution, 68% of the data fall within one average standard deviation. In this instance, the mean difference is 2 inches, while the average height of 7-year-old kids is 49 inches.
We must identify the range among heights that is within one average standard deviation in order to apply the scientific rule. To accomplish this, we can add and subtract the standard variance from the median as follows:
Mean ± (Standard Deviation) = 49 ± 2
As a result, the height range which falls within the standard deviation from the average is between 47 and 51 inches.
To know more about Column visit:
https://brainly.com/question/30544975
#SPJ1
5. In a fruit basket if there are 2 dozen bananas out of which 5 are
rotten, find the percentage of bananas which are in good
condition?
Answers
sin² x + cos²x = 1
Which Trigonometric Identity is given above?
- Pythagorean Identity
- Lagrange's Trigonometric Identity
- Angle Sum and Difference Identity
- Tangent Identity
Answers
The Trigonometric Identity sin² x + cos²x = 1 is: A. Pythagorean Identity.
What is Pythagorean Identity?The Pythagorean Identity which tend to asserts that for every angle x, the sum of the squares of the sine and cosine of x is equal to one is known as or called a trigonometric identity.
The Pythagorean identity can be expressed as:
sin² x + cos² x = 1
This identity is crucial to understanding trigonometry and tend to have several uses in numerous branches of science and engineering.
Therefore the correct option is A.
Learn more about Pythagorean Identity here:https://brainly.com/question/24287773
#SPJ1
The perimeter of a train ticket is 60 centimeters. It is 17 centimeters long. How tall is it?
Answers
If the perimeter of the train ticket is 60 centimeters and it's length is 17 centimeter long it's height is 13 centimeter
What is perimeter of a rectangle?A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length.
To find the perimeter of a rectangle we add all this sides together. This means that the perimeter of a rectangle is given as ;
P = l+l+w+w
P= 2(l+w)
60 = 2( 17+w)
60 = 2( 17+w)
17+w= 60/2
17+ w = 30
w = 30-17
w = 13cm
Therefore the height of the train ticket is 13cm
learn more about perimeter of a rectangle
https://brainly.com/question/10452031
#SPJ1
An object's motion is described by the equation d=3sin(8*pi*t)-2. The displacement, d, is measured in meters. The time, t, is measured in seconds. 1) What is the object's position (in meters) at t=0? 2) What is the object's maximum displacement (in meters) from its t=0 position? 3) How much time(in seconds) is required for one oscillation? 4) What is the frequency (measured in Hz) of this oscillation?
Answers
1. When t = 0, the position (displacement) of the object can be found by substituting t = 0 into the given equation of motion:d = 3sin(8π(0)) - 2 = 0 - 2 = -2 meters.2. The maximum displacement of the object from its t=0 position can be found by taking the amplitude of the displacement function. Since the function is of the form d = Asin(ωt) - B, where A is the amplitude, ω is the angular frequency and B is the vertical shift, it can be seen that the amplitude in this case is A = 3 meters. So, the maximum displacement is 3 meters.3. The time taken for one oscillation can be found by dividing the period, T, of the oscillation by the number of oscillations in that period. The period of the oscillation is the time taken for one complete cycle of the sine wave, which is 1/8 seconds. Thus, the time taken for one oscillation is:1 oscillation = T/1/8 s = 8T s4. The frequency of the oscillation is the reciprocal of the period, which is f = 1/T. Thus, the frequency is:f = 1/T = 1/(1/8) Hz = 8 Hz.
A student is attempting to write the statement below as an equation. Which of the following statements best applies to the sample mathematical work?
Statement: If 3 times a number is added to itself, the result is 30.
Work:
(1) Let x be the unknown quantity.
(2) The phrase "3 times a number" results in x + 3.
(3) The phrase "is added to itself" results in + x.
(4) Add these values from step 2 and step 3 togther and set that equal to 30.
A.
The interpretation in step 2 is incorrect or invalid.
B.
The interpretation in step 3 is incorrect or invalid.
C.
The interpretation in step 4 is incorrect or invalid.
D.
You cannot let x be the unknown quantity
Answers
Thus, the interpretation in step 4 is incorrect or invalid, and option C is the most appropriate choice.
The best statement that applies to the given mathematical work is option C: The interpretation in step 4 is incorrect or invalid.
In the work provided, steps 1 to 3 correctly interpret the given statement. Step 1 sets x as the unknown quantity,
step 2 correctly represents "3 times a number" as x + 3, and step 3 represents "is added to itself" as + x.
However, in step 4, the student incorrectly adds the values from step 2 and
step 3 together, resulting in x + 3 + x. This is an error because the phrase "is added to itself" refers to adding the unknown quantity to itself, which should be represented as 2x.
The correct equation should be:
x + 3 + x = 30
By combining like terms, we get:
2x + 3 = 30
For such more question on interpretation
https://brainly.com/question/29765108
#SPJ8
X-21=6 what does x equal??
Answers
Answer:
The answer is 27
Hope this helps
Answer:
x=27
Step-by-step explanation:
What you need to do is isolate the x or in other words have the x be alone on one side of the equal sign. To do this you would need to add 21 to both sides because you need to cancel out -21 with the opposite which would be positve 21. After that the x should be by itself and then finally add 21 to 6 to complete solving for x.
A cylinder has a surface area of 150 inches²? What is its height if the radius is 5 inches?
A) 5 inches
B) 10 inches
C)
\(5\pi \: inches\)
D)
\(10\pi \: inches\)
Answers
Answer:
10 inches
Step-by-step explanation:
did with a teacher
I’ll rate u 5 stars what is the slope intercept super easy and quick response

Answers
Answer:
Answer : y=2/3x-6
Step-by-step explanation:
Format : y = mx+b
The line has a y intercept at -6, so that will be our b.
our mx (slope) is formatted as y/x, so 2/3, which would result in 2/3x
Answer:
y=\(\frac{2}{3} \\ \)x-6
Step-by-step explanation:
Help please.
Algebra.

Answers
for this problem i did this:
4x+3y=-3
4(0)+3y=-3
3y=-3
y=-1
a simple way to find the y intercept is to make x equal 0 and then continue to solve the equation...if you were to solve for the y intercept you would make y equal 0 and then continue to solve the equation
(i hope that made sense)
What is the equation of a line that passes though the pointe (8, -3) and has a slope of 1/4?
Answers
Answer:
y = (1/4)x - 5
Step-by-step explanation:
We'll look for an equation having the form y=mx+b, where m is the slope and b is the y-intercept, the value of y when x=0.
We are told the slope, m, is (1/4):
y = (1/4)x+ b
We need to find a value of b such that it forces the line to go through point (8,-3). Enter that point in the equation:
y = (1/4)x + b
-3 = (1/4)(8) + b for (8,-3)
-3 = 2 + b
b = -5
The equation is y = (1/4)x - 5
See attached graph.

I JUST WANNA CHECK IF ITS CORRECT !!
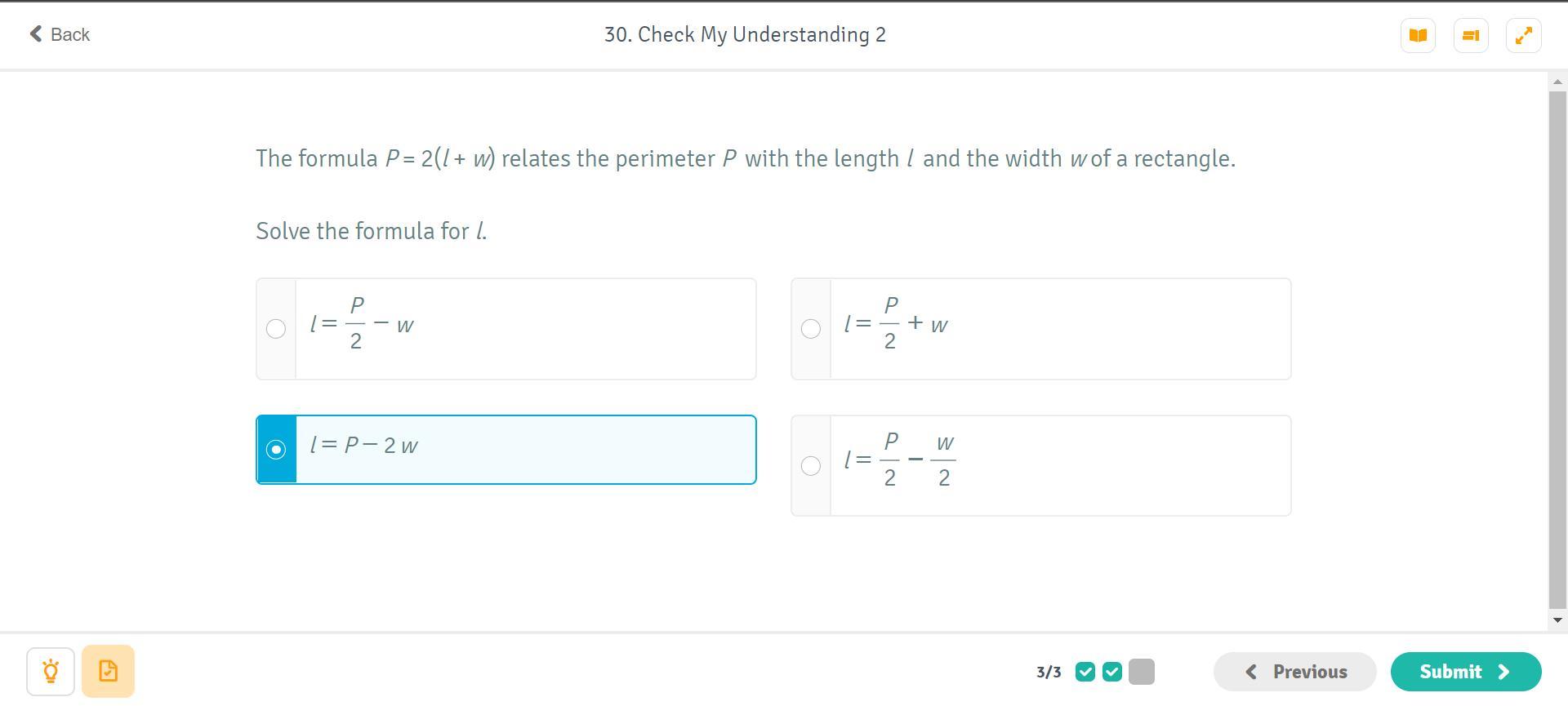
Answers
Answer:
I got the one above it: L=\(\frac{P}{2}\)-w
Step-by-step explanation:
To solve "P= 2(L+W)" , first distribute:
P= 2L+2W
Then get "2L" alone (by subtracting 2W from both sides):
P-2W= 2L-------- 2L= P-2W
Then divide by two to get just "L":
L= \(\frac{P}{2}\)-W
Hope this helps!
1. Factorise. a) x²-4
Answers
to factorize the expression \(x^2-4\) , we used the difference of squares formula to obtain \((x+2)(x-2)\) as the factors of the expression.
What is the factorization of equations?To factorize the expression \(x^2-4\) , we can use the difference of squares formula, which states that a² - b² can be factored as \((a + b)(a - b).\)
Using this formula, we can rewrite \(x^2-4\) as \((x + 2)(x - 2)\) , since \(x^2\) is like \(a^2\) and 4 is like \(b^2\).
Here's how we get to that answer:
\(x^2- 4 = (x^2 - 2^2)\) (writing \(4 as 2^2\))
\(= (x + 2)(x - 2)\) (using the difference of squares formula)
Therefore, \(x^2-4\) can be factored as \((x + 2)(x - 2).\)
Learn more about equations here:
https://brainly.com/question/1863222
#SPJ1
A unity feedback control system has a plant transfer function: G(s)=(s+2)∗(s2+8s+15)K(s+6) Determine the value of K so that the system will operate at 5% overshoot and settling time approximately at 2 seconds
Answers
The value of K that will make the system operate with a 5% overshoot and a settling time of approximately 2 seconds is 0.54.
To determine the value of K for a unity feedback control system to operate with a 5% overshoot and settling time of approximately 2 seconds, we need to calculate the desired damping ratio and natural frequency based on these specifications.
First, let's define the general form of a second-order transfer function for a unity feedback control system:
G(s) = Kωn² / (s² + 2ζωns + ωn²)
Here, K is the gain, ωn is the natural frequency, and ζ is the damping ratio.
To achieve a 5% overshoot, we know that the damping ratio ζ should be equal to 0.7. This is because the damping ratio determines the shape of the system's response, and a damping ratio of 0.7 corresponds to a critically damped response, which results in a 5% overshoot.
Next, we can use the settling time specification to determine the natural frequency ωn. The settling time is defined as the time it takes for the system's response to reach and stay within a certain percentage (usually 2%) of its final value. For a second-order system, the settling time can be approximated as:
Ts ≈ 4 / (ζωn)
Given that the settling time is approximately 2 seconds, we can solve for ωn:
2 = 4 / (0.7ωn)
ωn = 4 / (2 * 0.7) = 2.857 rad/s
Now that we have both the damping ratio ζ and the natural frequency ωn, we can find the value of K that satisfies these specifications.
Plugging the given plant transfer function G(s) = (s + 2)(s² + 8s + 15)K(s + 6) into the general form of the transfer function,
we can equate the coefficients to find K:
Kωn² = 15K -> K = ωn² / 15 = (2.857)² / 15 = 0.54
Therefore, the value of K that will make the system operate with a 5% overshoot and a settling time of approximately 2 seconds is 0.54.
To know more about damping ratio, click here
https://brainly.com/question/33300408
#SPJ11
This graph gives the growth of a plant over time. What is the slope of the line, and what does the slope mean in this situation?
Select from the drop-down menus to correctly complete the statement.
The slope is (), which means that the plant by () every day.
[Graph showing a line, extending from zero zero to seven three point five. There are points on the line at zero zero, two one, four two, and seven three point five. The vertical axis is labeled Growth and the horizontal axis is labeled Time.]--[This is shown in the image connected to this question]
{THIS IS FOR ANYBODY WHO NEEDS HELP!! I DO KNOW THE ANSWER! I'll be putting it in the answers, too.}

Answers
Answer:
The slope of the line is 2/3. In context of plant growth, every 3 days, the plant grows 2 inches.
Step-by-step explanation:
To find slope, you count the distance between y-values and x values. You then get a fraction of y over x.
Hope this helped and have a great day,
Ginny
The slope of the graph is 1/2, which means that the plant growth 1 inches in every 2 days.
What is Equation of line?
The equation of line passing through the points (x₁ , y₁) and (x₂, y₂) with slope m is defined as;
y - y₁ = m (x - x₁)
Where, m = (y₂ - y₁) / (x₂ - x₁)
Given that;
The points on the graph are (2, 1) , (4, 2) and (7, 3.5).
Now,
Since, Slope of the line passing through the points (x₁ , y₁) and (x₂, y₂) is,
⇒ m = (y₂ - y₁) / (x₂ - x₁)
Thus, The Slope of the line passing through the points (2, 1) and (4, 2) is,
⇒ m = (y₂ - y₁) / (x₂ - x₁)
⇒ m = (2 - 1) / (4 - 2)
⇒ m = 1 /2
Thus, The slope of the graph is 1/2, which means that the plant growth 1 inches in every 2 days.
Learn more about the slope visit:
https://brainly.com/question/16949303
#SPJ2
if we want to test for the significance of the model, the critical value of f at a 5% significance level is
Answers
To test for the significance of the model at a 5% significance level, the critical F value must be determined using the degrees of freedom and the F distribution table or statistical software. The calculated F value is then compared to the critical F value to determine if the model is statistically significant.
The significance of a model is determined by comparing the calculated F value to the critical F value at a given significance level. The critical F value is determined by the degrees of freedom for the numerator and denominator, and the significance level.
At a 5% significance level, the critical F value can be found using a F distribution table or a statistical software. The critical F value will be the value at which 95% of the F distribution falls below it, and 5% falls above it.
For example, if the degrees of freedom for the numerator are 2 and the degrees of freedom for the denominator are 10, the critical F value at a 5% significance level would be 4.10. If the calculated F value is greater than the critical F value, the model is considered to be statistically significant at the 5% level.
In conclusion, to test for the significance of the model at a 5% significance level, the critical F value must be determined using the degrees of freedom and the F distribution table or statistical software. The calculated F value is then compared to the critical F value to determine if the model is statistically significant.
Learn more about Significance Level
brainly.com/question/13947717
#SPJ11
Solve with steps please.
Urgenttt

Answers
You have to plug in -6 where x is.
35 + 2x = 60. HELP PLS
Answers
Answer:
=> x = 12.5Step-by-step explanation:
=> 35 + 2x = 60
=> 2x = 60-35
=> 2x = 25
=> x = 25/2
=> x = 12.5
35 + 2x = 60 - 35
2x = 25
/2 /2
X=12.5
The domain of the function given below is the set of all real numbers.
F(x)=[1/2]^x
A.true
B.false
Answers
Answer:
A. true.
The function f(x) = (1/2)^x can take any real number as an input, and the output will always be a real number. Therefore, the domain of the function is the set of all real numbers (-∞, +∞).
Answer:
A) True-------------------------
The given function is \(f(x) = (1/2)^x.\)
To determine whether its domain is the set of all real numbers, we need to examine the function and see if there are any restrictions on x.
In this case, the function is an exponential function with a base of 1/2. Exponential functions with a positive base are defined for all real numbers, as there are no restrictions on the exponent.
Therefore, the statement is true (option A).
Answer quickly IF u love god i do please

Answers
Answer:
The answer is 11
Step-by-step explanation:
The answer is 11 because you need to add the sides up that the points are on point P is 5 Point Q is 3 and point R is 3 5+3 is 8 8+3 is 11
Answer:
19.56
Step-by-step explanation:
PR = \(\sqrt{3^{2} + 3^{2} }\) = \(\sqrt{18}\) = 3\(\sqrt{2}\)
RQ = \(\sqrt{5^{2} +5^{2} }\) = \(\sqrt{50}\) = 5\(\sqrt{2}\)
QP = \(\sqrt{8^{2} +2^{2} }\) = \(\sqrt{68}\) = 2\(\sqrt{17}\)
Perimeter = sum of the sides = 3\(\sqrt{2}\) + 5\(\sqrt{2}\) + 2\(\sqrt{17}\) = 19.56
Break the triangle PQR into 3 right triangles, with each leg being a hypotenuse. Then you can use the Pythagorean theorem to find the length of each leg. Add them all together to get the perimeter.
'the largest prime number that is a factor of 42'
is multiplied by
'the smallest prime number that is a factor of 28'
Answers
Answer:
14.
Step-by-step explanation:
42 = 2 8 3 * 7
Largest prime factor = 7
28 = 2 * 2 * 7
Smallest prime factor = 2
Answer = 2*7 = 14.
What is the solution to the system of linear equations graphed below? On a coordinate plane, 2 lines intersect at (3.5, negative 4). (3 and one-half, negative 4) (Negative 4, 3 and one-half) (0, 3) (0, negative 4)
Answers
Answer:
Step-by-step explanation:
the answer is C just did the quiz
Answer:
its D i got it right on edge if there are any probs just tell me and i ll edit mark me brainleiest and hart and five stars please
Step-by-step explanation:
There were 5 seats on the bus. In how many ways could the seats be occupied if there were four children?
Answers
Answer:
5 choose 4
\(=\frac{5!}{4!\left(5-4\right)!}\) = 5
Step-by-step explanation:
Identify the slope from the equations y = -x -6
Answers
Answer:
The slope of the line is -1
I've attached a screenshot of a website that can solve function.
May I have brainliest please? :)

Maximize Z=12*1+16* 2 Subject to the constraints 10* 1 +20* 2
<=120; 8x_{1} + 8x_{2} <= 80 and x_{1}; x_{2} > 0 Solve
through graphical method
Answers
The optimal solution, obtained through graphical method, is: x₁ = 4, x₂ = 2, with the maximum value of Z = 80.
To solve the given linear programming problem graphically, we start by plotting the feasible region defined by the constraints:
Constraint 1: 10x₁ + 20x₂ ≤ 120
Constraint 2: 8x₁ + 8x₂ ≤ 80
Non-negativity constraint: x₁ ≥ 0, x₂ ≥ 0
The feasible region is the area of the graph that satisfies all the constraints.
Next, we calculate the objective function Z = 12x₁ + 16x₂. We plot the objective function as a line on the graph.
The optimal solution, which maximizes Z, is the point where the objective function line intersects the boundary of the feasible region.
To know more about optimal solution,
https://brainly.com/question/32645256
#SPJ11
Find the Euclidean Norm of the vector v=(1,2+i,−i) in Cn
.
Answers
The Euclidean Norm of the vector `v=(1,2+i,−i)` in `Cn` is `√(7)`.
We have the vector `v = (1,2+i,-i)`.The Euclidean Norm of the vector is
the square root of the sum of the absolute squares of its components.
The norm of v in `Cn` is calculated by the formula:
`||v|| = √(|1|² + |2+i|² + |-i|²)`
Here, |x| denotes the absolute value of x.
For `2 + i, the absolute square` is calculated as
`|2 + i|² = 2² + 1² = 4 + 1 = 5`
Similarly
For `-i`, the absolute square is calculated as:
`|-i|² = |i|² = 1`.
So, substituting these values in the equation,
we get:
`||v|| = √(|1|² + |2+i|² + |-i|²)= sqrt(1 + 5 + 1)
= √(7)`
you can learn more about Euclidean Norm at: brainly.com/question/15018847
#SPJ11
