Is -9.7 a rational number?
Answers
Related Questions
suppose you have a function of two variables, nand k; for instance h(n, k).if you are told that h(n, k)
Answers
Given a function of two variables, n and k, denoted as h(n, k), the function describes a mathematical relationship or operation that depends on the values of both n and k. Further details about the specific function, its definition, or purpose are required to provide a more comprehensive explanation.
A function of two variables, h(n, k), typically represents a mathematical relationship or operation that involves two independent variables, n and k. The specific form and purpose of the function can vary widely depending on the context or problem at hand.
To understand the behavior and properties of the function h(n, k), additional information is needed. This may include the mathematical expression defining the function, any constraints or conditions on the variables, and the intended interpretation or application of the function.
The function h(n, k) could represent various scenarios, such as a cost function in economics, a probability distribution in statistics, or a mathematical model in a scientific context. Without more details, it is challenging to provide a specific explanation or analysis of the function and its implications.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
If the sum of the interior angle
of a polygon with n
measures
sides is 1800°, find n.
n = [?]
Hint: Sum= (n-2)180
![If the sum of the interior angleof a polygon with nmeasuressides is 1800, find n.n = [?]Hint: Sum= (n-2)180](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/gWN22OvYSo2EO8PSAZNptrwBQtgbW3dA.png)
Answers
Answer:
The sum of the interior angles of a polygon with n sides is given by:
Sum = (n - 2) * 180
We are given that the sum of the interior angles is 1800 degrees. Setting these two expressions equal to each other, we get:
(n - 2) * 180 = 1800
Dividing both sides by 180, we get:
n - 2 = 10
Adding 2 to both sides, we get:
n = 12
Therefore, the polygon has 12 sides.
Given line l is a perpendicular bisector of ⎯⎯⎯⎯⎯⎯⎯⎯CB¯ and CB = 6.8, find DB.

Answers
For this problem, we are given a triangle with a line that bisects its base BC on point D. We need to determine DB using the fact that CB is equal to 6.8.
A bisector divides a segment in two equal parts. Since the line I bisects the segment CB, then it divides this segment in two equal parts such as:
\(\begin{gathered} CB=CD+DB\\ \\ CB=x+x\\ \\ CB=2x \\ \end{gathered}\)Since the value of CB is equal to 6.8, we have:
\(\begin{gathered} 6.8=2x\\ \\ 2x=6.8\\ \\ x=\frac{6.8}{2}=3.4 \end{gathered}\)The value of DB is equal to 3.4 cm.
Find the slope of the line passing through the points (4, 5) and (4. -6).
Answers
Answer:
Undefined
Step-by-step explanation:
The equation for slope is:
\(Slope = \frac{y_2-y_1}{x_2-x_1}\)
Let's plug the given points into the equation:
\(Slope = \frac{-6-5}{4-4}=\frac{-11}{0}\)
Since the change in x is 0, the slope is undefined
You sell a total of 17 pieces of disposable and washable face masks.what is the answer
Answers
3. A cable-stayed bridge is similar to a suspension bridge, but is more efficient for medium distances. In this design of bridge, there are two towers, and strong cables attach to the tops of the towers and the sides of the bridge. Assume the bridge is perpendicular to the two towers. a. Angle A is 35 degrees. Explain how you can find the measure of angles B, C, and D. (Hint: all angles in a triangle add to 180 degrees.) Can you find the measure of every angle on the bridge
Answers
The angle measures are A, B, C, D are 35, 55,55,55.
According to the statement
we have given that the bridge is perpendicular to the two towers. a. Angle A is 35 degrees.
And we have to find that the measure of angles B, C, and D.
So, For this purpose, we know that the
Angle A is 35 degrees and hint given is that the all angles in a triangle add to 180 degrees.
So,
A + B + X = 180
we know that A = 35 and X = 90 and
35 + B + 90 = 180
B = 180 - 90 - 35
B = 55
And
Now we find that the another angle Y.
So,
A + B + Y = 180
35 + 55 + Y = 180
Y = 90
Then
In order to calculate C, you have to make an assumption that was not given in the problem. The assumption is that triangles ABX and YCZ are mirror images of each other.
Then,
B = C = 55
And
and also since they are similar triangles,
D = C = 55.
So, The angle measures are A, B, C, D are 35, 55,55,55.
Learn more about Angles here
https://brainly.com/question/25770607
#SPJ4

how many poker hands consist of all face cards? (there are 12 face cards per deck, 52 cards in total per deck, and a poker hand consists of 5 cards) combinations
Answers
There are 792 poker hands consisting of all face cards.
To determine the number of poker hands consisting of all face cards, we need to consider the number of ways we can select 5 face cards from the 12 available face cards.
Since we are selecting a specific number of items from a larger set without considering the order, we can use combinations to calculate the number of poker hands.
The number of combinations of selecting k items from a set of n items is given by the formula:
C(n, k) = n! / (k!(n-k)!)
In this case, we want to select 5 face cards from the set of 12 face cards, so we can calculate:
C(12, 5) = 12! / (5!(12-5)!)
C(12, 5) = 12! / (5! * 7!)
Calculating the factorial terms:
12! = 12 * 11 * 10 * 9 * 8 * 7!
5! = 5 * 4 * 3 * 2 * 1
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1
Plugging in the values:
C(12, 5) = (12 * 11 * 10 * 9 * 8 * 7!) / (5 * 4 * 3 * 2 * 1 * 7!)
Simplifying the expression:
C(12, 5) = (12 * 11 * 10 * 9 * 8) / (5 * 4 * 3 * 2 * 1)
C(12, 5) = 792
Therefore, there are 792 poker hands consisting of all face cards.
To know more about probability visit :-
brainly.com/question/13604758
#SPJ1
The triangle on the grid will be translated two units down.
On a coordinate plane, triangle A B C has points (2, 1), (0, negative 1), (2, negative 1).
Which shows the triangle when it is translated two units down?
On a coordinate plane, triangle A prime B prime C prime has points (0, negative 1), (0, negative 3), (2, negative 3).
On a coordinate plane, triangle A prime B prime C prime has points (0, 1), (negative 2, negative 1), (0, negative 1).
On a coordinate plane, triangle A prime B prime C prime has points (2, negative 1), (2, negative 3), (0, negative 3).
On a coordinate plane, triangle A prime B prime C prime has points (2, negative 1), (2, negative 3), (0, negative 1).
Answers
Given:
The vertices of the triangle ABC are A(2, 1), B(0,-1), C(2, -1).
To find:
The vertices of the image of triangle ABC if ABC is translated two units down.
Solution:
It is given that the triangle ABC is translated two units down. So, the rule of translation is:
\((x,y)\to (x,y-2)\)
Using this rule, we get
\(A(2,1)\to A'(2,1-2)\)
\(A(2,1)\to A'(2,-1)\)
Similarly,
\(B(0,-1)\to B'(0,-1-2)\)
\(B(0,-1)\to B'(0,-3)\)
And,
\(C(2.-1)\to C'(2,-1-2)\)
\(C(2.-1)\to C'(2,-3)\)
The vertices of the image are A'(2,-1), B'(0,-3), C'(2,-3).
Therefore, the correct option is C.
Answer:
C.
Step-by-step explanation:
a restaurant offers a special pizza with any 6 toppings. if the restaurant has 14 topping from which to choose, how many different special pizzas are possible?
Answers
The number of different special pizzas possible is 3003.
To find this, you need to calculate the number of combinations of choosing 6 toppings from the 14 available. This can be represented using the combination formula, which is C(n, k) = n! / (k!(n-k)!), where n represents the total number of toppings (14) and k represents the number of toppings to choose (6).
1. Calculate factorial of n (14!): 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 87,178,291,200.
2. Calculate k! (6!): 6 x 5 x 4 x 3 x 2 x 1 = 720.
3. Calculate (n-k)! (8!): 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40,320.
4. Divide n! by (k!(n-k)!): 87,178,291,200 / (720 x 40,320) = 3003.
So, there are 3003 different special pizzas possible with 6 toppings from a choice of 14.
To know more about factorial click on below link:
https://brainly.com/question/30136880#
#SPJ11
Find the area of the shaded region. Use 3.14 for pi. Provide an answer
accurate to the nearest tenth.
10 ft
20 ft

Answers
Answer:
114 ft²
Step-by-step explanation:

Integrate the ODE
dy/dx = x² √y, 0 < x < 2, y(0) = 1
using Euler's method (Δx = 0, 2) to compute y(2). Obtain analytical solution to the ODE and compare y(2) obtained using Euler's method with that obtained analytically.
Answers
we find that the numerical approximation using Euler's method gives y(2) ≈ 1.865, while the analytical solution gives y(2) = 2.5.
Using the formula y(n+1) = y(n) + Δx * f(x(n), y(n)), where f(x, y) = x² √y, we can calculate the values of y at each step. Here's the step-by-step calculation:
Step 1: For x = 0, y = 1 (initial condition).
Step 2: For x = 0.2, y = 1 + 0.2 * (0.2)² * √1 = 1.008.
Step 3: For x = 0.4, y = 1.008 + 0.2 * (0.4)² * √1.008 = 1.024.
Step 4: For x = 0.6, y = 1.024 + 0.2 * (0.6)² * √1.024 = 1.052.
Step 5: For x = 0.8, y = 1.052 + 0.2 * (0.8)² * √1.052 = 1.094.
Step 6: For x = 1.0, y = 1.094 + 0.2 * (1.0)² * √1.094 = 1.155.
Step 7: For x = 1.2, y = 1.155 + 0.2 * (1.2)² * √1.155 = 1.238.
Step 8: For x = 1.4, y = 1.238 + 0.2 * (1.4)² * √1.238 = 1.346.
Step 9: For x = 1.6, y = 1.346 + 0.2 * (1.6)² * √1.346 = 1.483.
Step 10: For x = 1.8, y = 1.483 + 0.2 * (1.8)² * √1.483 = 1.654.
Step 11: For x = 2.0, y = 1.654 + 0.2 * (2.0)² * √1.654 = 1.865.
Therefore, using Euler's method with a step size of Δx = 0.2, we approximate y(2) to be 1.865.
To obtain the analytical solution to the ODE, we can separate variables and integrate both sides:
∫(1/√y) dy = ∫x² dx
Integrating both sides gives:
2√y = (1/3)x³ + C
Solving for y:
y = (1/4)(x³ + C)²
Using the initial condition y(0) = 1, we can substitute x = 0 and y = 1 to find the value of C:
1 = (1/4)(0³ + C)²
1 = (1/4)C²
4 = C²
C = ±2
Since C can be either 2 or -2, the general solution to the ODE is:
y = (1/4)(x³ + 2)² or y = (1/4)(x³ - 2)²
Now, let's evaluate y(2) using the analytical solution:
y(2) = (1/4)(2³ + 2)² = (1/4)(8 + 2)² = (1/4)(10)² = 2.5
Learn more about Integrate here : brainly.com/question/31744185
#SPJ11
An aquarium is 6900 cubic inches. Nathan wants to populate the aquarium with neon tetras and catfish. It is recommended that each neon tetra be allowed 170 cubic inches and each catfish be allowed 700 cubic inches of spaces. Nathan would like at least one catfish for every 4 neon tetras. Let x be the number of neon tetra and y be the number of catfish. Write the system of inequalities that describe the constraints.
Answers
I'm not sure hold on I'm thinking right now I'll get back to you when I actually know the answer this is kind of easy and a way to clean away so I'll get back to you later
Inequalities show a relationship between two numbers or two expressions.
The system of inequalities that describe the constraints are:
4x ≤ y
170x + 700y ≤ 6900
What are inequalities?It shows a relationship between two numbers or two expressions.
There are commonly used four inequalities:
Less than = <
Greater than = >
Less than and equal =
Greater than and equal=
Example:
2x > 4 is an inequality
3x + 4 < 5 is an inequality
We have,
Aquarium = 6900 cubic inches.
Neon tetra = 170 cubic inches.
Catfish = 700 cubic inches.
Let,
x = be the number of neon tetra.
y = be the number of catfish.
Nathan would like at least one catfish for every 4 neon tetras.
This can be written as:
4x ≤ y _____(1)
Now,
170x + 700y ≤ 6900 ______(2)
Thus,
The system of inequalities that describe the constraints are:
4x ≤ y
170x + 700y ≤ 6900
Learn more about inequalities here:
https://brainly.com/question/20383699
#SPJ2
A rectangular shape of dimension 95m by 75m is drawn to a scale of 1m to 10m. Find the area of the drawing
Answers
The area of the drawing as required to be determined in the task content is; 71.25 m².
What is the area of the drawing according to.the given scale?It follows from the task content that the area of the drawing is to be determined according to the given parameters.
Since the actual rectangular shape has dimensions 95m by 75m. Upon drawing using a scale of 1m to 10m.
It follows that the dimensions of the drawing becomes; 95/10 by 75/10.
Hence, since the dimension of the drawing by evaluation is; 9.5 by 7.5;
The area of the rectangle (A = l × b) is; 9.5 × 7.5 = 71.25 m².
Read more on Area of a rectangle;
https://brainly.com/question/16239445
#SPJ1
If the Brazoria County Fair had a weekend revenue of $12,000, how many dollars did the vendor fees being in?
Answers
Answer :
24,000$
Explanation: 12,000$ x 2 = 24,000$
I hope this helped and sorry if i’m wrong. ✨
4. this problem is also from ars magna. find two numbers such that the sum of their squares is 100. the square of the larger number is equal to the sum of the product of the larger number and four times the smaller number and eight times the larger number. let x and y be the two numbers such that x
Answers
The two numbers that satisfy both conditions are from quadratic equation :x =
1) -10/3, y = ±(10√7)/3
2)x = 10/3, y = ±(10√7)/3.
Let's denote the two numbers as x and y. We are given the following information:
1. The sum of their squares is 100: x^2 + y^2 = 100.
2. The square of the larger number is equal to the sum of the product of the larger number and four times the smaller number and eight times the larger number: y^2 = x(4y + 8x).
To solve this problem, we can start by simplifying the second equation. By expanding the equation, we get:
y^2 = 4xy + 8x^2.
Now, we can substitute this equation into the first equation to eliminatey:
x^2 + (4xy + 8x^2) = 100.
Combining like terms, we have:
9x^2 + 4xy - 100 = 0.
To find the values of x and y that satisfy this equation, we can use various methods such as factoring, completing the square, or the quadratic formula. In this case, let's solve it by factoring.
Factoring the quadratic equation, we get:
(3x + 10)(3x - 10) = 0.
Setting each factor equal to zero, we have two possibilities:
1. 3x + 10 = 0, which gives x = -10/3.
2. 3x - 10 = 0, which gives x = 10/3.
Now that we have the values of x, we can substitute them back into one of the original equations to find the corresponding values of y. Let's use the first equation:
For x = -10/3, we have (-10/3)^2 + y^2 = 100. Solving this equation, we find y = ±(10√7)/3.
For x = 10/3, we have (10/3)^2 + y^2 = 100. Solving this equation, we find y = ±(10√7)/3.
Therefore, the two numbers that satisfy both conditions are:
1. x = -10/3, y = ±(10√7)/3.
2. x = 10/3, y = ±(10√7)/3.
These are the two sets of numbers that meet the given conditions.
for more such question on quadratic equation visit
https://brainly.com/question/1214333
#SPJ8
PLEASE HELP WILL GIVE BRAINLIEST! Solve |3x – 1| = |x+1| by graphing.

Answers
it wold be (0,1) and (2,3)
Answer:
Step-by-step explanation:

Evaluate the expression using a calculator:

Answers
The value of the expression is 0.0265. Using exponents and power rules, the required value is calculated.
What are the exponent and power rules?The important exponent and power rules are:
a⁻ⁿ = 1/aⁿ; negative exponent(ab)ⁿ = aⁿ × bⁿ; power of a product ruleaⁿ × aˣ = aⁿ⁺ˣ; multiplication ruleaⁿ/aˣ = aⁿ⁻ˣ; division rule\(a^{\frac{x}{y} } = \sqrt[y]{a^x}\); fractional exponentCalculation:The given expression is \(126^{-3/4}\)
Using calculator: \(126^{-3/4}\) = 0.0265
Applying the exponent rule for evaluating the given expression:
\(126^{-3/4}\)
Applying the negative power rule;
I.e., a⁻ⁿ = 1/aⁿ
⇒ \(126^{-3/4}=\frac{1}{126^{3/4}}\)
Applying fractional exponent rule;
I.e., \(a^{\frac{x}{y} } = \sqrt[y]{a^x}\)
⇒ \(\frac{1}{126^{3/4}}=\frac{1}{\sqrt[4]{126^3} }\)
⇒ 1/\(\sqrt[4]{2000376}\)
⇒ 1/37.6077
⇒ 0.0265
Therefore, the value of the given expression is 0.0265.
Learn more about exponent rules here:
https://brainly.com/question/11975096
#SPJ1
which statement is not true
Answers
Answer:
where are the statements
Jen is investigating a quadratic function g(x). She writes four different forms of the function, as shown below. Select the form that reveals the maximum value of g(x) without having to be rewritten.
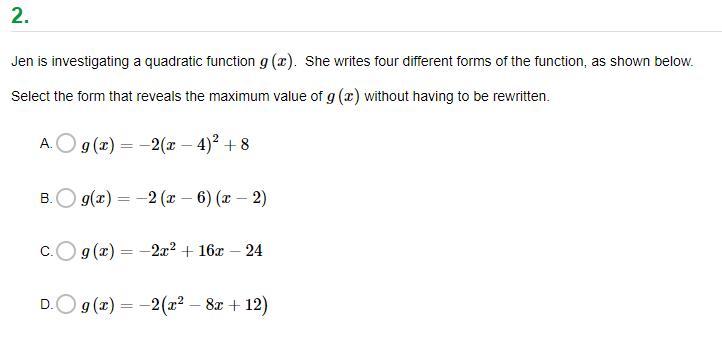
Answers
Answer:
A
Step-by-step explanation:
Since the coefficient of the x² term is negative (we know this because if you look at C, the coefficient of x² is -2, which is negative) we know that the vertex will be the maximum. To find the vertex without having to be rewritten, a quadratic function should be written in vertex form which is y = a(x - c)² + d where (c, d) is the vertex. The answer choice that is written in vertex form is A.
Question is in photo answer a through d please

Answers
The products written in scientific notation are:
a) \(5.88*10^9\)
b) \(15*10^{12}\\\)
c) \(8.4*10^{-10}\)
d) \(42*10^{-7}\)
How to take the products?The first product we need to solve is:
\((4.2*10^6)*(1.4*10^3)\)
We can reorder that product into the one below:
\((4.2*1.4)*(10^6*10^3)\)
The exponents in the right side are added, so we get:
\((4.2*1.4)*(10^6*10^3) = 5.88*10^{3 + 6} = 5.88*10^9\)
Now let's do the same in the others.
b)
\((5*10^5)*(3*10^7)\\= 5*3*10^{5 + 7}\\= 15*10^{12}\\\)
Now we need to write the first number between 0 and 10, then we can rewrite this as:
\(1.5*10^{13}\)
c) Again doing the same thing.
\((4*10^{-3})*(2.1*10^{-7}})\\= 4*2.1*10^{-3 - 7}\\= 8.4*10^{-10}\)
d) Finally, this last product is:
\((6*10^{-2})*(7*10^{-5}})\\= 6*7*10^{-2 - 5}\\= 42*10^{-7}\)
Again we need to have a number between 0 and 10, so we can rewrite this as:
\(4.2*10^{-8}\)
Learn more about scientific notation at:
https://brainly.com/question/5756316
#SPJ1
why are named constants used, rather than numbers, for token codes?
Answers
Named constants are used rather than numbers for token codes because they make the code more readable and easier to understand.
Constants are also used to avoid any errors that may occur if a number is mistyped. By using named constants, it is easier to update the value of the constant if it needs to be changed in the future. Additionally, using named constants can help prevent mistakes, such as accidentally using the wrong number in a calculation. Overall, named constants provide a more organized and efficient way of coding.
For example, consider the following code:
const int BLUE = 2;
const int GREEN = 3;
Instead of using the numbers 1, 2, and 3 in the code, we can use the named constants RED, BLUE, and GREEN. This makes the code more readable and easier to understand. If we need to change the value of one of the constants, we can simply update the value in one place, rather than having to search through the entire code for all instances of the number.
To know more about token codes click here:
https://brainly.com/question/29981815
#SPJ11
4. Lin runs 4 laps around a track in 9 minutes at a constant speed.
A. How many minutes per lap is that? (1 point)
B. How many laps per minute is that? (1 point)
C. How long would it take Lin to run 15 laps at the same rate? (1 point)
Answers
Answer:
Number of minutes per lap = 2.25 minute
Number of lap per minute = 0.444 lap (Approx)
Time taken for 15 lap = 33.75 minutes
Step-by-step explanation:
Given:
Number of laps = 4
Time taken = 9 min
Computation:
Number of minutes per lap = 9 / 4
Number of minutes per lap = 2.25 minute
Number of lap per minute = 4 / 9
Number of lap per minute = 0.444 lap (Approx)
Time taken for 15 lap = 15 x 2.25
Time taken for 15 lap = 33.75 minutes
(co 4) a company manufacturers soda cans with a diameter of 52 millimeters. in a sample of 18 cans, the standard deviation was 2.3 millimeters. what would be the 96% confidence interval for these cans?
Answers
The 96% confidence interval for the soda cans' diameters is 51.02 mm to 52.98 mm.
To calculate the 96% confidence interval, follow these steps:
1. Identify the sample size (n = 18), sample mean diameter (52 mm), and standard deviation (2.3 mm).
2. Find the standard error (SE) by dividing the standard deviation by the square root of the sample size: SE = 2.3 / sqrt(18) ≈ 0.54 mm.
3. Determine the z-score for a 96% confidence interval using a z-table or calculator, which is approximately 1.96.
4. Calculate the margin of error (ME) by multiplying the z-score by the standard error: ME = 1.96 * 0.54 ≈ 1.06 mm.
5. Determine the lower and upper limits of the confidence interval by adding and subtracting the margin of error from the sample mean diameter: 52 - 1.06 = 51.02 mm, and 52 + 1.06 = 52.98 mm.
To know more about confidence interval click on below link:
https://brainly.com/question/29680703#
#SPJ11
If F(2) = 10 And F'(X) = X^2f(X) For All X, Find F"(2). Show Your Work.
Answers
Therefore, the solution of the problem of the function ƒ"(2) come out to be 200.
What is function?For some time now, you've been experimenting with equations of the "y=" variety. You've also noticed that the "pleasant" equations are the ones you can solve for "y=" and then input into your graphing calculator, such as straight lines as opposed to ellipses. They are functions, these "y=" equations.
Here,
Given ƒ(2) = 10
and_ƒ'(x) = \(x^{2}\)ƒ(x)
thus we differentiate it with respect to x
then ƒ'(2) = 22ƒ(2) = 4×10=40
then we again differentiate it with respect to x
ƒ"(x) = \(x^{2}\)ƒ'(x)+2xf(x)
ƒ"(2) = 22ƒ (2)+2×2ƒ(2)=4×40+4x10=160+40
ƒ"(2) = 200
Therefore, the solution of the problem of the function ƒ"(2) come out to be 200.
To know more about function ,visit
https://brainly.com/question/29120892
#SPJ4
Plz, help me ASAP!! NO FILES period!

Answers
Answer:
Step-by-step explanation:
what do u need help with
Answer:
simplify expression
Step-by-step explanation:
1-9/7n
Which best describes what the Central Limit Theorem states? The distribution of means of random samples pulled from a population will be normally distributed if the sample size is large enough. All distributions have the same mean. The distribution of standard deviations of random samples pulled from a population will be normally distributed if the sample size is large enough. All distributions are close enough to normally distributed to use the normal distribution as a approximation.
Answers
The statement that best describes the Central Limit Theorem is (a) The distribution of means of random samples pulled from a population will be normally distributed if the sample size is large enough.
The Central Limit Theorem (CLT) states that if repeated random samples is taken from a population with a finite mean and standard deviation, then the distribution of the sample means will approach a normal distribution, even if the original population is not normally distributed.
The larger the sample size, the more closely the sample means will approximate a normal distribution.
which means that, for example, if we take multiple samples of size 100 from a population and calculate the average of each sample, the distribution of those sample means will be approximately normally distributed, regardless of the original shape of the population.
The given question is incomplete , the complete question is
Which best describes what the Central Limit Theorem states ?
(a) The distribution of means of random samples pulled from a population will be normally distributed if the sample size is large enough.
(b) All distributions have the same mean.
(c) The distribution of standard deviations of random samples pulled from a population will be normally distributed if the sample size is large enough.
(d) All distributions are close enough to normally distributed to use the normal distribution as a approximation.
Learn more about Central Limit Theorem here
https://brainly.com/question/18403552
#SPJ4
Maya's final score is 298.Which dancer has the greater final score?
Answers
Answer:
the question
Step-by-step explanation:
because it litterly has dancer and in the question it has the greater final score.
definite integral of (2)^(0) f x sqrt16 − x4 dx; u = x2 by u substitution
Answers
The definite integral ∫(0 to 2) f(x)√(16 - x^4) dx, using u-substitution (u = x^2), simplifies to ∫(0 to 4) f(√u)√(16 - u^2) (1/2) du. The specific value of the integral depends on the function f(x) provided.
To solve the integral ∫(0 to 2) f(x)√(16 - x^4) dx using u-substitution, we begin by letting u = x^2. This choice of substitution allows us to simplify the expression and integrate with respect to u instead of x.
First, we need to find the differential du in terms of dx. Differentiating u = x^2 with respect to x, we have du = 2x dx.
Next, we substitute u and du into the integral. The limits of integration will also change accordingly. When x = 0, u = (0)^2 = 0, and when x = 2, u = (2)^2 = 4. The new integral becomes ∫(0 to 4) f(x)√(16 - x^4) dx = ∫(0 to 4) f(√u)√(16 - u^2) (1/2) du.
Now, we can evaluate the integral with respect to u, and then substitute back u = \(x^{2}\) to obtain the final result.
Learn more about integration here:
https://brainly.com/question/31744185
#SPJ11
What does it mean when my dog is eating grass???
Answers
Answer:
Their stomach is upset. they eat the grass to calm their stomach. Don't worry it is good if your dog eats grass because that helps the dog's health out. Grass gives them vitamins and nutrients that helps their bowel system. seriously let you dog eat the grass, they will be okay. my four dogs do it as well and they feel better after. hope this helps
how do you solve this question

Answers
Let the ceilings be a & b
and the distance from one corner of the ceiling to the opposite be c
then using Pythagoras theorem
\(c = \sqrt{a {}^{2} + b {}^{2} } \\ c = \sqrt{16 {}^{2} + 12 {}^{2} } \\ c = \sqrt{256 + 144 } \\ c = \sqrt{400} \\ c = 20\)
hence ,c .°. the distance from one corner of the ceiling to the opposite is 20