In the circle below, suppose m VUX = 228° and mZUVW=121°. Find the following.
U
X
(a) m/VUX = °
(b) m LUXW =
0.

Answers
Assume that m arc VUX = 228° and m ∠UVW = 121° in the circle below.
m∠VUX = 66° and m m∠UXW = 59° respectively.
1) The given information is;
The angle of arc m∠VUX = 228°, the measured angle of ∠UVW = 121°
Given that m∠VUX = 228°, therefore, arc ∠XWV = 360 - 228 = 132°
Therefore, the angle subtended by arc ∠XWV at the centre = 88°
The angle subtended by arc ∠XWV at the circumference = m∠VUX
∴ m∠VUX = 132°/2 = 66° (Angle subtended at the center = 2×angle subtended at the circumference)
m∠VUX = 66°
2) Similarly, m∠XWV is subtended by arc m∠VUX, therefore, m∠XWV = (arc m VUX)/2 = 228°/2 = 114°
A quadrilateral's angles add up to 360°.
Therefore;
m∠VUX + m∠XWV + m∠UVW + m∠UXW = 360° (The sum of angles in a quadrilateral XWVU)
m∠UXW = 360° - (m∠VUX + m∠XWV + m∠UVW)
m∠UXW = 360° - (66 + 114 + 121)
m∠UXW = 360° - 301
m∠UXW = 59°.
To learn more about the arc, refer:-
https://brainly.com/question/18741430
#SPJ1
Related Questions
Select all the points that are on the line through (0, 5) and (2, 8).
(4, 11)
(5, 10)
(6, 14)
(30, 50)
(40, 60)
Answers
I hope this helps if it is right
6. Cindy is 2 years older than Marie. Their ages total 30 old is each person?
Answers
Answer:
huh? no they cant both be 30 at the same time is cindy is 2 years older than marie....
Step-by-step explanation:
Find the value of tan M rounded to the nearest hundredth, if necessary.

Answers
Answer:
36.9
Step-by-step explanation:
Use the formula \(a^2 + b^2 = c^2\) to find the length of LK.
40 is the hypothenuse because it is directly across from the right angle.
\(a^2 + 24^2 = 40^2\)
\(a^2\) = 32
Tan is opposite over hypothenuse.
Tan M = 36.9
11. Find x, y, and z.
5
y
6
3

Answers
Answer:
x = z = 3√5y = 4Step-by-step explanation:
You want the missing segment lengths in the kite shown, where half-diagonals are 3 and 6, and one side length is 5.
KiteThe diagonals of a kite cross at right angles, so each of the triangles shown is a right triangle. The figure has left-right symmetry about the vertical axis, so x=z.
Length yWe recognize the top triangles as being 3-4-5 right triangles, so the missing side length is y = 4.
Lengths x and zThese lengths are the hypotenuse of a right triangle with legs 3 and 6. The Pythagorean theorem tells us they are ...
x² = 3² +6²
x² = 9 +36 = 45
x = √(45) = √(9·5) = 3√5
The lengths x and z are ...
x = z = 3√5
__
Additional comment
In case you have never heard of a 3-4-5 right triangle, you can find y from the Pythagorean relation:
5² = 3² +y²
y² = 25 -9 = 16
y = √16 = 4
The {3, 4, 5} Pythagorean triple is one of several in common use in algebra, trig, and geometry problems. Others include {5, 12, 13}, {7, 24, 25}, {8, 15, 17}.
Find the volume of the cylinder. Either enter an exact answer in terms of 7 or use 3.14 for pi

Answers
Answer:
45.29 units.
The graph below represents taxi fares in the city of Chicago. If a woman travels 8.5 miles by taxi, what would you expect her fare to be? Give an estimate to the nearest dollar.

Answers
ANSWER:
$22
STEP-BY-STEP EXPLANATION:
To determine the value of the fare we use it through the graph just like this:
Therefore, the correct option is $22

The function P(h) = 21h represents the total salary at a rate of $21 per
hour, P. as a function of the number of hours worked, h.
Find the total salary, when the number of hours worked is 34.
Answers
Replace h with 34:
p(h) = 21(34)
Multiply :
21x 34 = 714
Answer: $714
Two events, A and B, are such that P(A) = 0.25, P(B) = 0.35 and P(AUB) = 0.5. Find: a P(ANB) b P(ANB) Chapter review probability short answer question 7 b
Answers
The probability of the intersection of events A and B, P(A ∩ B), is 0.10.
To find the probability of the intersection of events A and B, P(A ∩ B), we can use the formula:
P(A ∩ B) = P(A) + P(B) - P(A ∪ B)
Given:
P(A) = 0.25
P(B) = 0.35
P(A ∪ B) = 0.5
Substituting the values into the formula:
P(A ∩ B) = 0.25 + 0.35 - 0.5
P(A ∩ B) = 0.10
Hence, the above equation is also correct. The value of P(A ∪ B) is 0.5. The value of P(A ∩ B) is 0.1.
Therefore, the probability of the intersection of events A and B, P(A ∩ B), is 0.10.
To know more about probability refer here:
https://brainly.com/question/31828911#
#SPJ11
a rectangular storage container with an open top is to have a volume of 12 cubic meters. the length of its base is twice the width. material for the base costs 10 dollars per square meter. material for the sides costs 6 dollars per square meter. find the cost of materials for the cheapest such container.
Answers
The cost of materials for the cheapest container is $184.67.
Suppose the width is x and it is given that the length of its base is twice the width, so the length of the base is 2x.
The base area is 2x².
Since the volume is $12m³
The height has to be 12/ 2x² = 6/ x²
The cost of making such a container is.
cost of base = 2x² × 10
= 20x²
The cost of sides =( 2 × 2x 6/x² + 2 × x × 6 / x²) 6
= (24/x + 12/x )6
= 36/x × 6
216/x
The overall cost is hence the sum of the base and the sides = f(x)
= 20x² + 216/x
To get the minimum,
df(x) / dx = 20x² + 216/x = 0
= 40x - 216/x² = 0
x³ = 216/40
= 54/10
= 27/5
x = 3/∛5
= 3/ 1.70
= 1.76
f(x) = 20(1.76)² + 216/ 1.76
= 61.952 + 122.72
= 184.67
Therefore we get the cost of the materials to be $184.67.
To know more about the function refer to the link given below:
https://brainly.com/question/11624077
#SPJ4
a function is a relation in which each possible input value leads to exactly one output value. the input values make up the range and the output values make up the domain
Answers
A relation between sets is referred to as a function when there is exactly one output for each input.
Which statement is true?A function is a relation where each output value is assigned to exactly one input value.The domain of a function is the set of all output values, or y-values, for which the function is defined.The range of a function is the set of all input values, or x-values, for which the function is defined.To write the equation y = ax + b in function notation, substitute f(x) for y.?To write the equation y = ax + b in function notation, substitute f(x) for y
The only true statement is the last one. A function assigns exactly one output value to each input value. The domain is the set of all input, or x-values. The range is the set of all output, or y-values.
y=ax+b can be written in function notation by replacing y with f(x).
To know more about Function , visit :
ttps://brainly.com/question/17810174
#SPJ4
Find the line parallel to y=2x+2 that include the point (3,-1)
Answers
Answer:
y = 2x - 7
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = 2x + 2 ← is in slope- intercept form
with slope m = 2
• Parallel lines have equal slopes , then
y = 2x + c ← is the partial equation
to find c substitute (3, - 1 ) into the partial equation
- 1 = 2(3) + c = 6 + c ( subtract 6 from both sides )
- 7 = c
y = 2x - 7 ← equation of parallel line
give me the answer of this picture

Answers
Step-by-step explanation:
81 x 24 + 19 x 24 - 2400
since 81 and 19 are multiplying the same number, so we can do
(81+19) x 24 - 2400
100 x 24 - 2400
2400 - 2400
0
Find the value of B that makes the fraction equivalent
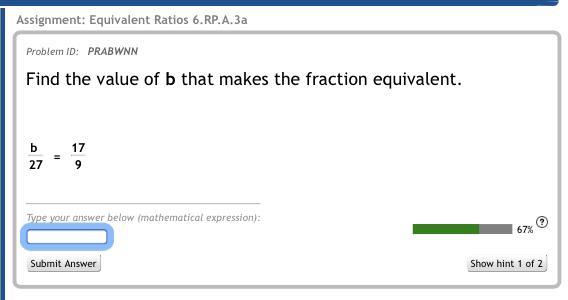
Answers
Answer:
b = 51
Step-by-step explanation:
b/27 = 17/9
27/9 = 3
We need to multiply the right side by 3/3 to get to the left
17/9 * 3/3
51/27
need help with this asap!

Answers
Answer:
Step-by-step explanation:
1 ) 2 + 7t [ there are no like terms , so no further simplifying ]
2) 6r + ( - 16 r )
= 6 r - 16 r [ both are like terms ]
= - 10 r
3) (3x + 2 ) + ( 2x - 4 )
= 3x + 2 + 2x - 4
= 3x + 2x - 4 + 2 [ arranging like terms together ]
= 5x - 2
4) (8 n² - 3 n + 6 ) + ( n - 2 )
= 8n² - 3n + 6 + n - 2
= 8n² - 3n + n + 6 - 2 [ bringing like terms together ]
= 8n² - 2n + 4
Answer:
1.) 2 + 7 t
2.) - 10 r
3.) 5 x - 2
4.) 8 n² - 2 n + 4
Step-by-step explanation:
1.) 2 + 7 t
No like terms, so no further simplifying.
2.) 6 r + ( - 16 r )
6 r - 16 r. ... ( combine like terms)
- 10 r
3.) ( 3 x + 2 ) + ( 2 x - 4 )
= 3 x + 2 + 2 x - 4
combine like terms
= 3 x + 2 x - 4 + 2
= 5 x - 2
4.) ( 8 n ² - 3 n + 6 ) + ( n - 2 )
= 8 n² - 3 n + 6 + n - 2
combine like terms
= 8n² - 3 n + n + 6 - 2
= 8 n² - 2 n + 4.
Can you please help me

Answers
Answer:
Q1: equal
Q2: smaller
Q3:equal
Q4 smaller
Q5: bigger
Step-by-step explanation:
Samra's guardians invested money for her into a 529 College Savings Plan, which compounds annually. The growth of the savings plan per year, x, can be represented by the exponential function f(x) = 500(1.03)x. What is the meaning of the y-intercept in the context of the problem?
The percent rate of change is 500%.
The initial value of the investment is $500.
The principal amount put into the savings plan is $1.03.
The average rate of change that is occurring is 1.03.
Answers
The y-intercept of the given exponential function would be represents the initial value of the investment is $500 which is the correct option (B).
What is an exponential function?An exponential function is defined as a function whose value is a constant raised to the power of an argument is called an exponential function.
It is a relation of the form y = aˣ in mathematics, where x is the independent variable
The given exponential function f(x) = 500(1.03)ˣ
Here x would be represented growth of the savings plan per year
To determine the y-intercept of the function
We have to substitute the value of x = 0 in the given function,
⇒ f(x) = 500(1.03)⁰
⇒ f(x) = 500(1)
⇒ f(x) = 500
Therefore, the y-intercept of the given exponential function would be represents the initial value of the investment is $500.
Learn more about exponential function here:
brainly.com/question/11487261
#SPJ1
please help me ASAP!!!
Answers
To solve the equation we first squared both sides of it, that is:
\(\begin{gathered} (\sqrt[]{x+3})^2=(x+1)^2 \\ x+3=x^2+2x+1 \\ x^2+2x+1-x-3=0 \\ x^2+x-2=0 \end{gathered}\)Now we can use the general formula for quadratic equations, then:
\(\begin{gathered} x=\frac{-1\pm\sqrt[]{1^2-4(1)(-2)}}{2(1)} \\ =\frac{-1\pm\sqrt[]{1+8}}{2} \\ =\frac{-1\pm\sqrt[]{9}}{2} \\ =\frac{-1\pm3}{2} \\ \text{then} \\ x=\frac{-1+3}{2}=\frac{2}{2}=1 \\ or \\ x=\frac{-1-3}{2}=-\frac{4}{2}=-2 \end{gathered}\)Now that we found two option for x, we have to check which of them is really a solution for the original equation (we have to do this since we squared the original equation to get rid of the root), to do this we plug the values we found to see if the eqaution holds.
If x=1:
\(\begin{gathered} \sqrt[]{1+3}=1+1 \\ \sqrt[]{4}=2 \\ 2=2 \end{gathered}\)hence x=1 is a solution for the original equation.
If x=-2:
\(\begin{gathered} \sqrt[]{-2+3}=-2+1 \\ \sqrt[]{1}=-1 \\ 1=-1 \end{gathered}\)since this is not true, x=-2 is not a solution for the original equation.
Therefore, the solution for the equation is x=1.
Difficult for me but should be easy for some big brain out there

Answers
Answer:
I would say the last one
Step-by-step explanation:
Answer:
42/45
Step-by-step explanation:
Two lengths are in ratio 7:8.if the first length is 273. What amount is the second length
Answers
Answer:
312
Step-by-step explanation:
Since the ratio is 7:8, mark it as 7x:8x.
Now, they said that the first length is 273. Solve the equation:
7x=273
x=39
Substitute it into 8x. 39*8=312. That's your answer.
PLS MARK BRANILIEST!!!
Find the greatest common factor for each problem.use the t-chart to slow?
16 and 40
Gcf:
Answers
The required GCF is 8.
The greatest common factor is that greatest number from the factors which divides the number completely.
For example take numbers 12 and 16.
The factors of 12 are 2×2×3.
And the factors of 16 are 2×2×2×2.
We can clearly see that the common factors are 2×2 which gives 4. So, 4 is the greatest common factor which divides both 12 and 16.
Here it is given to find the greatest common factor of 16 and 40.
Factors of 16 = 2×2×2×2
Factors of 40 = 2×2×2×5
We can see clearly the common factors are 2×2×2 which gives 8.
So, 8 is the greatest common factor.
To learn more about the factors visit the link :
https://brainly.com/question/24182713
#SPJ9
What is the simplified form of the expression? 15y−3(4y+10) 3y−30 27y+10 3y+10 27y−30
Answers
Answer:
3y-30
Step-by-step explanation:
How Many Cups In A Pounds ?
Answers
Answer:
There are 1.91 cups in a pound
Could someone Help pleasee ??!

Answers
Answer:
sorry if im wrong
Step-by-step explanation:
no
no
yes
yes
Find the coordinates of the vertex of the parabola
y²+4y-2x=6
Answers

The t-statistic or t-ratio is used to test the statistical significance overall regression model used to test the statistical significance of each β i used to test to see if an additional variable which has not been observed should be included in the regression model is close to zero when the regression model is statistically significant none of the above
Answers
The correct statement is:
The t-statistic or t-ratio is used to test the statistical significance of each β_i in a regression model.
The t-statistic is calculated by dividing the difference between the sample mean and the hypothesized population mean by the standard error of the sample mean.
The formula for the t-statistic is as follows:
t = (sample mean - hypothesized population mean) / (standard error of the sample mean)
The t-statistic or t-ratio is used to test the statistical significance of each β_i (regression coefficient) in a regression model. It measures the ratio of the estimated coefficient to its standard error and is used to determine if the coefficient is significantly different from zero.
Learn more about t-statistic or t-ratio:
https://brainly.com/question/30466889
#SPJ11
For the following figure, find x (if your answer has a decimal, round to the tenths place);

Answers
The length of one part of BC is approximately x = 4 units.
What is the median of the triangle?
In a triangle, a median is a line segment that joins a vertex to the midpoint of the opposite side. Each triangle has three medians, and they all intersect at a single point called the centroid.
Let ABC be the given triangle with AB = 5, AC = 7, and BC = 8. Let D be the midpoint of BC so that AD is a median of triangle ABC.
Since AD is a median, it divides BC into two equal parts. Let x be the length of one part of BC, so the other part has a length 8 - x.
Then, we have:
x + 8 - x = 8
Simplifying, we get:
8 = 8
This equation is true, so our assumption that x is one part of BC is correct.
Now, we can use the Pythagorean theorem to find x. Let E be the foot of the altitude from A to BC, so that AE is perpendicular to BC. Then, we have:
BE² + AE² = AB² (by the Pythagorean theorem)
CE² + AE² = AC² (by the Pythagorean theorem)
Since D is the midpoint of BC, we have:
BE = CE = BC/2 = 8/2 = 4
Therefore, the length of one part of BC is approximately x = 4 units.
To learn more about the median of a triangle visit:
https://brainly.com/question/2288141
#SPJ1
Jack Insurance leases a copying machine for $45 per day that is used by all individuals at their office. An average of five persons per hour arrives to use this
machine, with each person using it for an average of eight minutes. Assume the interarrival times and copying times are exponentially distributed.
What is the probability that a person arriving to use the machine will find it idle?
O A.
0.3333
О B.
0.6666
O C.
0.7777
O D.
0.2222
Answers
The probability that a person arriving to use the machine will find it idle is 1/3 or 0.3333. Option a is correct.
Use the concept of an M/M/1 queue to calculate the probability, which models a single-server queue with exponential interarrival times and exponential service times.
In this case, the interarrival time follows an exponential distribution with a rate parameter of λ = 5 persons per hour (or 1/12 persons per minute). The service time (copying time) also follows an exponential distribution with a rate parameter of μ = 1/8 persons per minute (since each person uses the machine for an average of 8 minutes).
In an M/M/1 queue, the probability that the system is idle (no person is being served) can be calculated as:
P_idle = ρ⁰ × (1 - ρ), where ρ is the traffic intensity, defined as the ratio of the arrival rate to the service rate. In this case, ρ = λ/μ.
Plugging in the values, we have:
ρ = (1/12) / (1/8) = 2/3
P_idle = (2/3)⁰ × (1 - 2/3) = 1/3
Therefore, the probability is 1/3 or approximately 0.3333.
Thus, option (A) is the correct answer.
Learn more about probability https://brainly.com/question/31828911
#SPJ11
find the euler equation that represents the relationship between current-period consumption and future-period consumption in the optimum.
Answers
The Euler equation represents the relationship between current-period consumption and future-period consumption in the optimum. It is derived from intertemporal optimization in economics.
In the context of consumption, the Euler equation can be expressed as:
u'(Ct) = β * u'(Ct+1)
where:
- u'(Ct) represents the marginal utility of consumption in the current period,
- Ct represents current-period consumption,
- β is the discount factor representing the individual's time preference,
- u'(Ct+1) represents the marginal utility of consumption in the future period.
This equation states that the marginal utility of consumption in the current period is equal to the discounted marginal utility of consumption in the future period. It implies that individuals make consumption decisions by considering the trade-off between present and future utility.
Note: The Euler equation assumes a constant discount factor and a utility function that is differentiable and strictly concave.
To know more about marginal utility related question visit:
https://brainly.com/question/30841513
#SPJ11
Please help me!
Find the value of x for the rectangle.

Answers
Answer:
36
Step-by-step explanation:
When 3/11 is written as a repeating decimal, which digits are repeating? A. 27 B. 37 C. 73 D. 28
Answers
Answer: A. 27
Step-by-step explanation:
3/11 = .27272727...
when you divide by 11 you can think of the numerator being multiplied by 9
9 x 3 = 27 so 3/11 is .27 repeating
example: 2 x 9 = 18 and 2/11 is .18 repeating
Answer:
a 27
Step-by-step explanation: