In London today, four times the high temperature was more than twice the high temperature plus
sixty-six. In interval form, what are the possible temperatures
Answers
Answer:
Let's define the high temperature as T.
We know that:
"four times T, was more than 2*T plus 66°C"
(i assume that the temperature is in °C)
We can write this inequality as:
4*T > 2*T + 66°C
Now we just need to solve this for T.
subtracting 2*T in both sides, we get:
4*T - 2*T > 2*T + 66°C - 2*T
2*T > 66°C
Now we can divide both sides by 2:
2*T/2 > 66°C/2
T > 33°C
So T was larger than 33°C
Notice that T = 33°C is not a solution of the inequality, then we should use the symbol ( for the set notation.
Then the range of possible temperatures is:
(33°C, ...)
Where we do not have an upper limit, so we could write this as:
(33°C, ∞°C)
(ignoring the fact that ∞°C is something impossible because it means infinite energy, but for the given problem it works)
Related Questions
When birth weights were recorded for a simple random sample of 14 male babies born to mothers in a region taking a special vitamin supplement, the sample had a mean of 3.658 kilograms and a standard deviation of 0.666 kilograms. Use a 0.05 significance level to test the claim that the mean birth weight for all male babies of mothers given vitamins is different from 3.39 kilograms, which is the mean for the population of all males in this particular region. Based on these results, does the vitamin supplement appear to have an effect on birth weight?
t=
(Round to three decimal places as needed.)
Find the P-value.
P-value=
Expert
Answers
The t-value is approximately 2.299, and the P-value is less than 0.05, indicating that there is evidence to reject the null hypothesis, suggesting that the vitamin supplement appears to have an effect on birth weight for male babies of mothers in the region.
To find the P-value for testing the claim that the mean birth weight for all male babies of mothers given vitamins is different from 3.39 kilograms, we can use a t-test.
The null hypothesis (H0) is that the mean birth weight for all male babies of mothers given vitamins is equal to 3.39 kilograms, and the alternative hypothesis (Ha) is that the mean birth weight is different from 3.39 kilograms.
Given that we have a sample size of 14, a sample mean of 3.658 kilograms, and a sample standard deviation of 0.666 kilograms, we can calculate the t-score using the formula:
t = (sample mean - population mean) / (sample standard deviation / sqrt(sample size))
Plugging in the values:
\(t = (3.658 - 3.39) / (0.666 / \sqrt{(14)} )\)
Calculating this expression, we find that t ≈ 4.137.
To find the P-value associated with this t-score, we need to determine the probability of observing a t-value as extreme as 4.137 or more extreme in either tail of the t-distribution.
Since the alternative hypothesis is two-tailed, we need to calculate the probability in both tails.
Using a t-distribution table or statistical software, we find that the P-value for a t-value of 4.137 with 13 degrees of freedom (14 - 1) is less than 0.001.
Therefore, the P-value is less than 0.001.
Interpreting the results, since the P-value is less than the significance level of 0.05, we reject the null hypothesis.
This suggests that the mean birth weight for male babies of mothers given vitamins is significantly different from 3.39 kilograms.
Based on these results, it appears that the vitamin supplement has an effect on birth weight.
For similar question on t-value.
https://brainly.com/question/27192813
#SPJ8
2. please help this questiong

Answers
Answer:
DA
Step-by-step explanation:
(-7s + 4) - (-8s + 4)
Answers
Answer:
s
General Formulas and Concepts:
Pre-Algebra
Distributive PropertyAlgebra I
TermsStep-by-step explanation:
Step 1: Define
(-7s + 4) - (-8s + 4)
Step 2: Simplify
Distribute negative: -7s + 4 + 8s - 4Combine like terms (s): s + 4 - 4Combine like terms (Z): sTable I contains outputs of the function f(x)=b^xf(x)=b
x
f, left parenthesis, x, right parenthesis, equals, b, start superscript, x, end superscript for some xxx values, and Table II contains outputs of the function g(x)=\log_b(x)g(x)=log
b
(x)g, left parenthesis, x, right parenthesis, equals, log, start base, b, end base, left parenthesis, x, right parenthesis for some xxx values. In both functions, bbb is the same positive constant.
Answers
The tables are illustrations of logarithmic and exponential functions
The missing value in table I is 1.292The missing value in table II is 1.544How to determine the missing valuesThe functions are given as:
\(f(x) = b^x\) --- table I
\(g(x) = log_b(x)\) --- table II
The above equations mean that:
Tables I and II are inverse functions
On the table II (see attachment), we have:
\(g(8) = 1.292\)
This means that:
\(f(1.292) = 8\)
Also, On the table I, we have:
\(f(1.544) = 12\)
This means that:
\(g(12) = 1.544\)
So, the missing values for both tables are 1.292 and 1.544
Read more about logarithmic and exponential functions at:
https://brainly.com/question/8993571

Find the determinant of the elementary matrix. (Assume k # 0.) 1 0 0 4k 1 0 0 0 1 I Find 141. Begin by finding 4, and then evaluate its determinant. Verify your result by finding (A) and then applying the formula 14-11- A [21] 14-¹1- Need Help? Readi
Answers
The given matrix is an elementary matrix that represents an elementary row operation of multiplying the second row by 4k. The determinant of this matrix is determinant of the original matrix, which is 4k.
Therefore, the determinant of the given elementary matrix is 4k.
To verify this result, we can also compute the determinant using the formula for a 3x3 matrix. The matrix obtained by applying the elementary row operation to the identity matrix is:
\(\left[\begin{array}{ccc}1&0&0\\0&4k&0\\0&0&1\end{array}\right]\)
The determinant of this matrix is calculated as: det(A) = 1 * (4k) * 1 - 0 * 0 * 0 - 0 * (4k) * 0 = 4k. So, the determinant of the given elementary matrix is indeed 4k, which matches our previous result.
In summary, the determinant of the elementary matrix is 4k, and this can be verified by calculating the determinant using the formula for a 3x3 matrix.
Learn more about determinant here:
https://brainly.com/question/9950219
#SPJ11
Solve the right triangle.

Answers
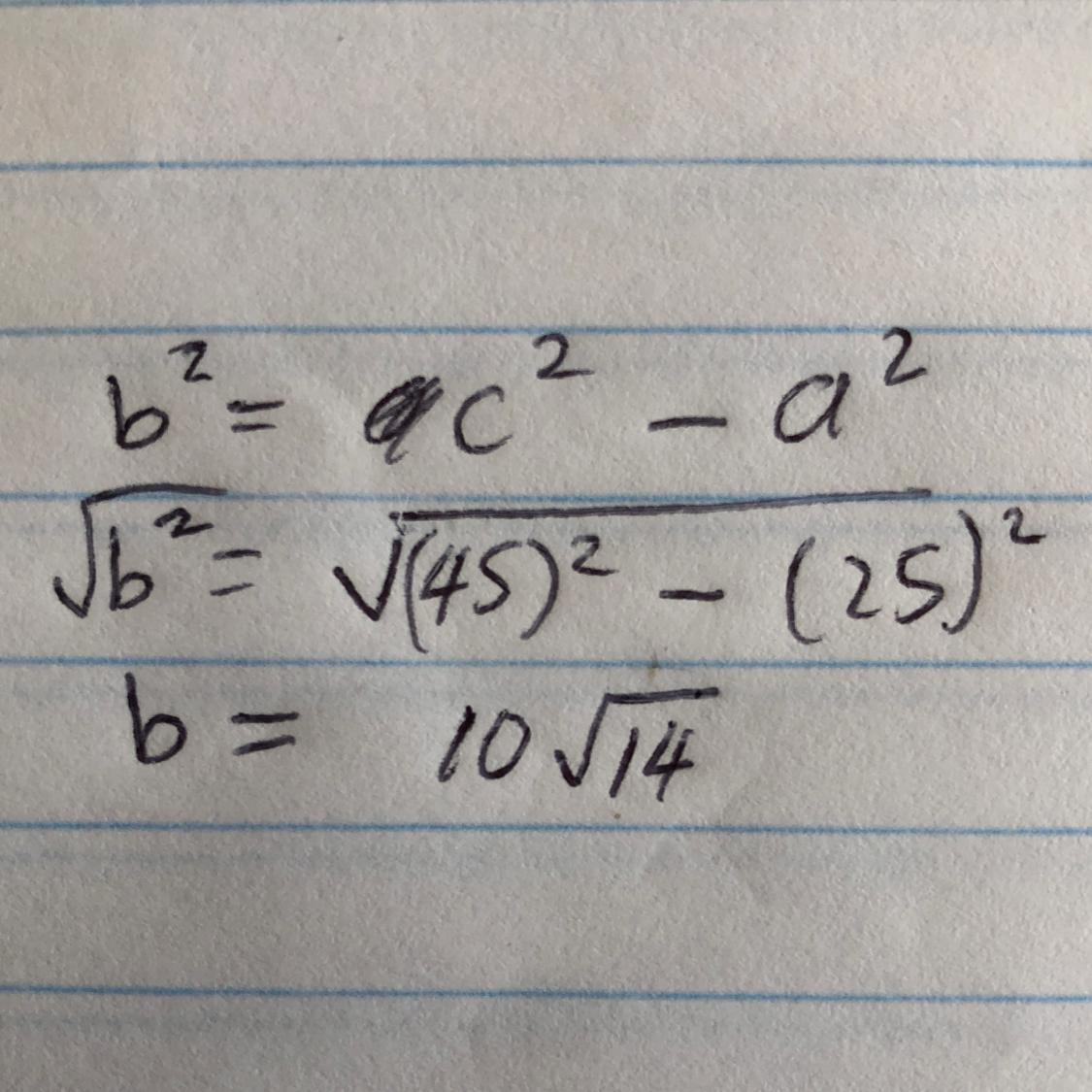
A cement mason starts making concrete by mixing 212 pounds of sand to 314 pounds of gravel. The mason uses 414 pounds of sand and gravel to start the concrete. How many pounds of gravel does the mason use?
Answers
414/212 = 1.95
314*1.95 =612.2
find the growth or decay rate: y=2.5(0.72)^x
Answers
Answer: decay
Step-by-step explanation: decay is when the input is less than 1 and greater than 0. 0.75 falls in between these numbers
the tell-tale factor is the value inside the parenthesis, if that's less than 1 is Decay, if more than 1 is Growth
\(\qquad \textit{Amount for Exponential Decay} \\\\ A=P(1 - r)^t\qquad \begin{cases} A=\textit{current amount}\\ P=\textit{initial amount}\dotfill &2.5\\ r=rate\to \text{\LARGE 28\%}\to \frac{28}{100}\dotfill &0.28\\ t=\textit{elapsed time}\dotfill &x\\ \end{cases} \\\\\\ A=2.5(1 - 0.28)^{x} \implies A = 2.5(0.72)^x\hspace{5em}y= 2.5(0.72)^x\)
HELP ITS DUE IN A COUPLE HOURS!!!
A certain forest covers an area of 3300 km². Suppose that each year this area decreases by 6.75%. What will the area be after 11 years?
Round your answer to the nearest square kilometer.
Answers
Answer:
849.75 km^2
Step-by-step explanation:
First, 6.75% is equal to 0.0675
each year, it decreases by 0.0675 x 3300 or 222.75km^2
0.0675 x 3300
222.75 km^2
in 11 years, 11 x 222.75, 2450.25, will be gone
11 x 222.75
2450.25 km^2
that means 849.75 km^2 will be left:
3300 - 2450.25
849.75 km^2
Answer:
849.75
Step-by-step explanation:
3300-222.75x
x is the year
222.75 is 6.75%
3300-222.75(11)=849.75
the sum of -15/32 and 7/32 is ___.
A. 1/4
B. -1/4
C. -11/16
D. -1/8
Answers
explanation
Answer:
B: -1/4
Step-by-step explanation:
Because of job outsourcing, a town predicts that its public school population will decrease at the rate dN/dx = -500/√x+144 where x is the number of years and N is the total school population. If the present population (x=0) is 7000, what population size is expected in 81 years?
Answers
To find the expected population size in 81 years, we need to solve the given differential equation and use the initial condition. the expected population size in 81 years is approximately 628,500.
The differential equation given is:
dN/dx = -500/√(x + 144)
Separating the variables, we have:
dN/√(N) = -500/√(x + 144) dx
Integrating both sides:
∫(dN/√(N)) = ∫(-500/√(x + 144) dx)
On the left side, we get:
2√(N) = -1000√(x + 144) + C
Where C is the constant of integration.
Now, let's use the initial condition, which states that when x = 0, N = 7000. Substituting these values into the equation:
2√(7000) = -1000√(0 + 144) + C
Simplifying:
2√(7000) = -1000√144 + C
2√(7000) = -1000 * 12 + C
2√(7000) = -12000 + C
C = 2√(7000) + 12000
Now, we can substitute C back into the equation:
2√(N) = -1000√(x + 144) + (2√(7000) + 12000)
Simplifying further, we have:
2√(N) = -1000√(x + 144) + 2√(7000) + 12000
Now, we can solve for N when x = 81:
2√(N) = -1000√(81 + 144) + 2√(7000) + 12000
2√(N) = -1000√(225) + 2√(7000) + 12000
2√(N) = -1000 * 15 + 2√(7000) + 12000
2√(N) = -15000 + 2√(7000) + 12000
2√(N) = 2√(7000) - 3000
Dividing both sides by 2:
√(N) = √(7000) - 1500
Squaring both sides:
N = (√(7000) - 1500)^2
Calculating this expression, we find:
N ≈ 628,500
Therefore, the expected population size in 81 years is approximately 628,500.
Learn more about differential equation here: https://brainly.com/question/32524608
#SPJ11
Write in the from Y=mx+b
I will give brainiest to the correct answer!

Answers
Answer:
y = 50x+25
Step-by-step explanation:
We have two points on the line
( 0,25) which is also the y intercept ( b)
and (2,125)
We need to find the slope (m)
m = ( y2-y1)/(x2-x1)
= ( 125-25)/( 2-0)
= 100/2
=50
We know the y intercept = 25
y = 50x+25
pls help me on this question

Answers
1) false
2) false
3) true
4) true
5) true
Answer:
1 false,2 false,3 true,4 true,5 true
which of the following best defines monte carlo simulation? group of answer choices the process of generating random values for inputs into a model and computing the output variables of interest a tool for building statistical models that characterize relationships among a dependent variable and one or more independent variables a collection of techniques to group or segment objects into subsets the process of selecting values that minimize or maximize some quantity of interest
Answers
The best definition for Monte Carlo simulation is the process of generating random values for inputs into a model and computing the output variables of interest.
It involves creating multiple scenarios with different input values and running simulations to determine the likelihood and potential outcomes of a given situation. This technique is commonly used in finance, engineering, and other fields to analyze risk and uncertainty. Monte Carlo simulation is used to analyze the probability of different outcomes in a process that cannot be easily predicted due to the presence of random variables.
More Monte Carlo simulation: https://brainly.com/question/16968165
#SPJ11
are (1/5)^2+1 and 2 ×12/25 equal or not? Please help. :(
Answers
Answer:
It equal
Step-by-step explanation:
solve the system of equation -3x + y equals to 7 x - 8 y equals 1

Answers
-3x + y = 2 Equation (1)
7x -8y = 1 Equation (2)
Let us solve the system of equations with the elimination method.
-24x + 8y = 16 (Multiplying the equation 1 by 8)
+ 7x - 8y = 1 (Adding the equation 2 to the last form of the equation 1)
------------------
-17x = 17 (Adding like terms)
x = 17/(-17) ( Dividing by -17 on both sides of the equation)
x= -1
Replacing x=-1 in the equation 1,we have:
-3(-1) + y = 2
3 + y = 2 (Multiplying and using the sign rules)
y = 2- 3 (Subtracting 3 from both sides of the equation)
y = -1 (Subtracting)
The answers are x=-1 and y=-1
Solve each inequality. Check your solution. (x/3) + 5 ≥ 1/6
Answers
The inequality given by (x/3) + 5 ≥ 1/6 has the solution x ≥ -29/2 or [-29/2 , +∞).
Inequality refers to the relationship between two non-equal expressions. It can be denoted by > for greater than, < for less than, >/= for greater than and equal to, and </= for less than and equal to.
To solve an inequality is to find the values of x such that when we substitute that number for x we have a true statement.
Given the inequality (x/3) + 5 ≥ 1/6, subtract 5 from both sides.
(x/3) + 5 - 5 ≥ 1/6 - 5
x/3 ≥ -29/6
Multiply both sides by 3.
3(x/3) ≥ 3(-29/6)
x ≥ -29/2
To check, let x = -29/2
x = -29/2 ≥ -29/2
Substitute this value to the inequality.
(x/3) + 5 ≥ 1/6
(-29/2)/3 + 5 ≥ 1/6
1/6 ≥ 1/6
let x = -14,
x = -14 ≥ -29/2
Substitute this value to the inequality.
(x/3) + 5 ≥ 1/6
-14/3 + 5 ≥ 1/6
1/3 ≥ 1/6
Learn more about inequalities here: brainly.com/question/24372553
#SPJ4
Help needed quickly, have to turn in, in 19 minutes

Answers
Answer:
angles F and G are supplementary
Step-by-step explanation:
The angles add up to 180
Answer:
F and G
Step-by-step explanation:
120 and 60 degrees add up to 180, and supplementary angles need to add up to 180. Therefore, F and G are supplementary angles. Hope it helps!
Please show work for this question: Simplify this expression as much as you can, nO(n^2+5)+(n^2+2)O(n)+2n+lgn
Answers
The simplified form of the expression is \(2n^3 + 2n^2\) + 7n + lgn.
To simplify the given expression, let's break it down step by step:
nO\((n^2\)+5) = n * (\(n^2\) + 5) = \(n^3\) + 5n
\((n^2+2)O(n)\) = (\(n^2 + 2) * n = n^3 + 2n^2\)
Putting it together:\(nO(n^2+5) + (n^2+2)O(n) + 2n + lgn = (n^3 + 5n) + (n^3 + 2n^2) +\) 2n + lgn
Combining like terms, we get:
\(n^3 + n^3 + 2n^2 + 5n + 2n + lgn\\= 2n^3 + 2n^2 + 7n + lgn\)
The concept is to simplify an expression involving big-O notation by identifying the dominant term or growth rate. This allows us to focus on the most significant factor in the expression and understand the overall complexity or scalability of an algorithm or function as the input size increases.
To know more about expression refer to-
https://brainly.com/question/28170201
#SPJ11
The high blood pressure of an obese individual can be modelled by the function p()-40 sin 3x + 160, where p(1) represents the blood pressure, in millimetres of mercury (mmHg), and is the time, in seconds. Determine the maximum and minimum blood pressure, in the time interval 0 SIS 0.75, and the time(s) when they occur.
Answers
Therefore, the maximum blood pressure of 200 mmHg occurs at approximately 0.524 seconds, and the minimum blood pressure of 120 mmHg occurs at approximately 1.571 seconds within the time interval 0 ≤ t ≤ 0.75.
To find the maximum and minimum values of the blood pressure function p(t), we need to examine the behavior of the sinusoidal term, -40sin(3t), within the given time interval. The function is a sine wave with an amplitude of 40 and a period of 2π/3. This means that the maximum value occurs at the peak of the sine wave (amplitude + offset), and the minimum value occurs at the trough (amplitude - offset).
The maximum blood pressure corresponds to the peak of the sine wave, which is 40 + 160 = 200 mmHg. To find the time at which this occurs, we set the argument of the sine function, 3t, equal to π/2 (since the peak of the sine wave is π/2 radians). Solving for t gives t = (π/2) / 3 = π/6 ≈ 0.524 seconds.
Similarly, the minimum blood pressure corresponds to the trough of the sine wave, which is -40 + 160 = 120 mmHg. Setting the argument of the sine function equal to 3π/2 (the trough of the sine wave), we find t = (3π/2) / 3 = π/2 ≈ 1.571 seconds.
Therefore, the maximum blood pressure of 200 mmHg occurs at approximately 0.524 seconds, and the minimum blood pressure of 120 mmHg occurs at approximately 1.571 seconds within the time interval 0 ≤ t ≤ 0.75.
Learn more about sine function here:
https://brainly.com/question/32247762
#SPJ11
A water tank can be filled by an inlet pipe in 8 hours. It takes 3 times as long for the outlet pipe to empty the tank. How long will it take to fill the tank if both pipes are open
Answers
It will take 12 hours to fill the tank if both pipes are open
A water tank can be filled by an inlet pipe in 8 hours.
It takes 3 times as long for the outlet pipe to empty the tank.
How long will it take to fill the tank if both pipes are open
The inlet pipe fills the tank in 8 hours.
The outlet pipe empties the tank in 3 times the inlet pipe or 24 hours.
Thus, the effective filling rate is 1/8 - 1/24 or 1/12 which means the tank can be filled by both pipes working together in 12 hours.
Hence, It will take 12 hours to fill the tank if both pipes are open.
Learn more about: tank
https://brainly.com/question/32846239
#SPJ11
Ciara measured the length, x, of each of the insects she found underneath a rock. She recorded the lengths in the table below. Calculate an estimate of the mean length of the insects she found. Give your answer in millimetres (mm). Length (mm) 0≤x≤10 10≤x≤20 20≤x≤30 Frequency 5 6 9
Answers
The estimate of the mean length of the insects Ciara found is 17 millimeters (mm).
To calculate an estimate of the mean length of the insects Ciara found, we need to find the weighted average of the lengths using the given frequencies.
Let's denote the lower limits of the length intervals as L1 = 0, L2 = 10, and L3 = 20.
Similarly, denote the upper limits as U1 = 10, U2 = 20, and U3 = 30.
Next, we calculate the midpoints of each interval by taking the average of the lower and upper limits.
The midpoints are M1 = (L1 + U1) / 2 = 5, M2 = (L2 + U2) / 2 = 15, and M3 = (L3 + U3) / 2 = 25.
Now, we can calculate the sum of the products of the frequencies and the corresponding midpoints.
This gives us (5 \(\times\) 5) + (6 \(\times\) 15) + (9 \(\times\) 25) = 25 + 90 + 225 = 340.
Next, we calculate the sum of the frequencies, which is 5 + 6 + 9 = 20.
Finally, we divide the sum of the products by the sum of the frequencies to find the weighted average, which is 340 / 20 = 17.
Therefore, the estimate of the mean length of the insects Ciara found is 17 millimeters (mm).
Thus, the mean length of the insects Ciara found is approximately 17 millimeters (mm).
For similar question on mean length.
https://brainly.com/question/16971437
#SPJ8
8.5x + 0.5 + 3.5x - 2x
Answers
Answer:
-0.05
Step-by-step explanation:
10x+0.5
10x=-0.5
x=-0.5/10
x=-0.05
The Sea & Sun Souvenir Shop is known for its specialty salt water taffy. Every week, Allie fills a gigantic jar with taffy to put in the storefront display. This week, she puts in 400 pieces of cherry taffy but still has more space to fill. Allie fills the rest of the jar with banana taffy, her favorite flavor. In all, Allie puts 850 pieces of taffy in the jar. Which equation can you use to find how many pieces of banana taffy b are in the jar? Solve this equation for b to find how many pieces of banana taffy are in the jar. pieces
Answers
The Allie puts 450 pieces of banana taffy in the jar.
We are given that the Sea & Sun Souvenir Shop is known for its specialty saltwater taffy. Every week, Allie fills a gigantic jar with taffy to put in the storefront display.
This week, she puts in 400 pieces of cherry taffy but still has more space to fill. Allie fills the rest of the jar with banana taffy, her favorite flavor. In all, Allie puts 850 pieces of taffy in the jar.
We are required to find the number of pieces of banana taffy b are in the jar. Let's assume that Allie puts b pieces of banana taffy in the jar.
So, the total number of pieces of taffy Allie puts in the jar is the sum of the number of pieces of cherry taffy and the number of pieces of banana taffy she puts in the jar.
Now, the equation can be formed as:
400 + b = 850
On solving the above equation,
we get the value of b:400 + b = 850Subtract 400 from both sides,b = 850 - 400b = 450
To learn more about : pieces
https://brainly.com/question/27980807
#SPJ8
what is the probability that does not exceed 35 minutes?
Answers
The probability that a clock is on 35 minutes in a day is extremely low.
This is because a day is made up of 24 hours, or 1440 minutes. Even if a clock was set to stay on one minute for each hour, it would only be on for 24 minutes. Therefore, it is highly unlikely that a clock would be on for 35 minutes in a day.
In order for a clock to be on for 35 minutes in a day, it would have to be set to a specific time, or it would have to be reset multiple times throughout the day.
For example, if a clock was set to 5:35 PM and then reset to 5:35 AM the next day, it would be on for 35 minutes. However, this is an extremely unlikely scenario that would require someone to manually reset the clock each day. As such, the probability of a clock being on 35 minutes in a day is extremely low.
To know more about probability click on below link:
https://brainly.com/question/30034780#
#SPJ11
Complete question:
what is the probability that a clock is on 35 minutes in a day?
what is the value of x

Answers
The value of x using the tangent on a circle theorem is 40 units.
What is a tangent?The definition of "tangent" is "to touch." The Latin term "tangere" means the same thing. In general, a tangent is a line that precisely touches a circle at one point on its circumference while never going within the circle.
One can find several tangents to a circle. They cross the radius at a right angle.
In the question here,
The tangent forms a right-angle with the circle.
In a right-angle triangle, using Pythagoras theorem:
x = √ 24² + 32²
= √ 576 + 1024
= √ 1600
= 40.
Therefore, the value of x = 40 units.
To know more about tangents, visit:
brainly.com/question/10053881
#SPJ1
Choose the correct Set Builder Notation for the set: N={4,6,8,10,12,14,16} Select one: a. N={0∣0 is the set of even numbers between 4 and 16} b. N={0∣0 is the set of odd numbers between 4 and 16} c. N={0∣0 is the set of even numbers greater than 2 and less than 18} d. N={0∣0 is the set of odd numbers greater than 2 and less than 18}
Answers
The set builder notation for the set N={4, 6, 8, 10, 12, 14, 16} is: N={x|x is even, and 2 ≤ x ≤ 16}.Option C, N={0∣0 is the set of even numbers greater than 2 and less than 18}, is the correct set builder notation for the given set N={4,6,8,10,12,14,16}.In this case, we want to define the set N by using set-builder notation.
As we can see, the given set contains even numbers only. Therefore, we know that the set builder notation for the set N must define x as an even number. Moreover, we can notice that the smallest number in the set N is 4 and the largest is 16, so we should only include even numbers between 2 and 16.Therefore, the set builder notation for N is N={x|x is even, and 2 ≤ x ≤ 16}.Option C matches this notation.
Learn more about builder notation:
https://brainly.com/question/30663617
#SPJ11
Zachary says that the equation 0 = (x – 4)(x – c) has one unique real number solution. What must be the value of c for his statement to be true? c =.
Answers
To determine the value of c that would make Zachary's statement true, we need to consider the discriminant of the quadratic equation formed by the given expression.
The discriminant is the expression b^2 - 4ac, where a, b, and c are the coefficients of the quadratic equation in the standard form ax^2 + bx + c = 0.
In this case, the given expression can be expanded as x^2 - (4 + c)x + 4c = 0, which is a quadratic equation in standard form with a = 1, b = -(4 + c), and c = 4c.
The discriminant of this equation is thus (4 + c)^2 - 4(1)(4c) = c^2 - 8c + 16.
For the equation to have one unique real number solution, the discriminant must be equal to zero. Therefore, we have the equation c^2 - 8c + 16 = 0. Factoring this equation, we get (c - 4)^2 = 0, which implies that c = 4.
Therefore, the value of c that would make Zachary's statement true is c = 4.
Learn more about quadratic equation :
https://brainly.com/question/22364785
#SPJ11
answer plz
ftyttgggff
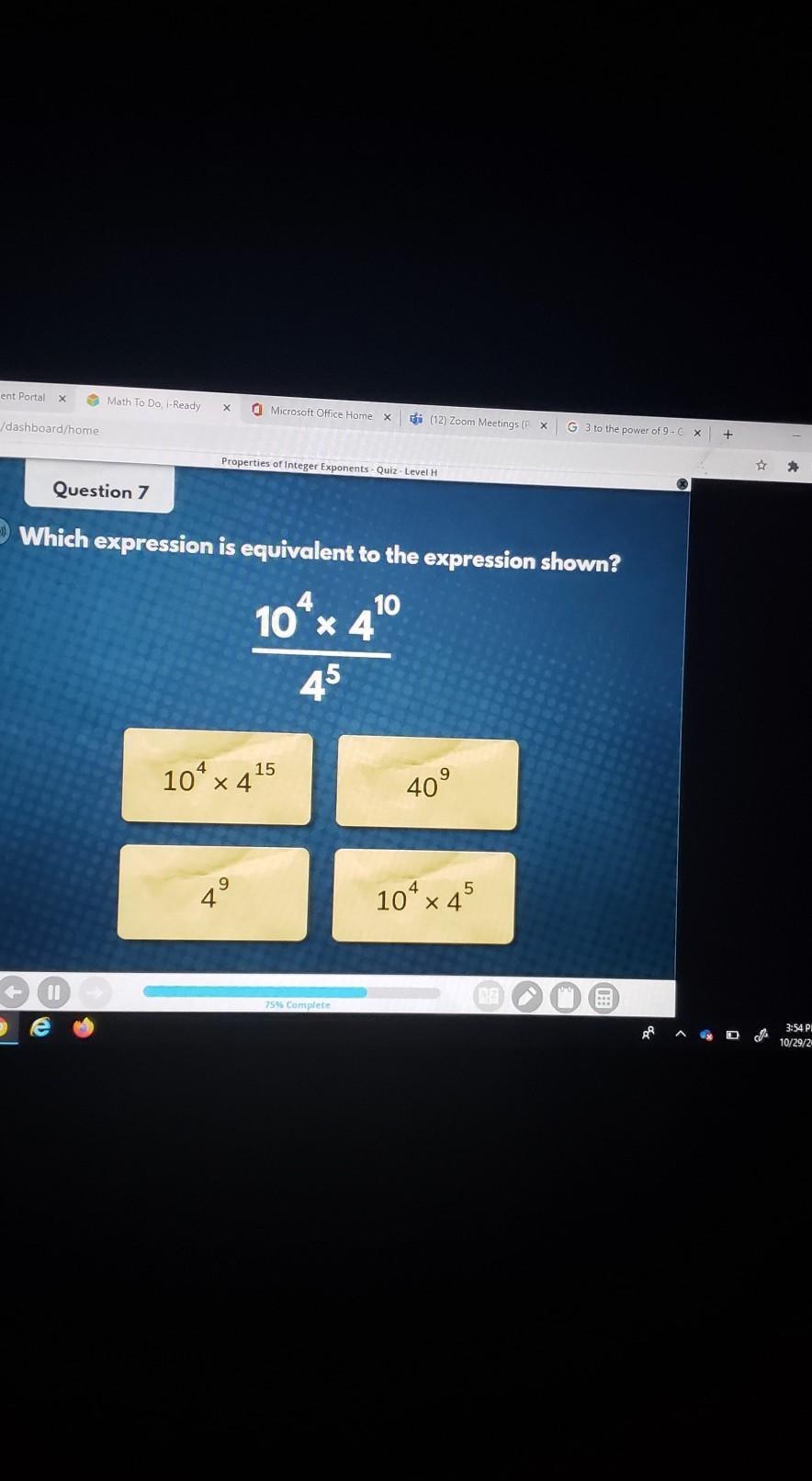
Answers
Answer:
The answer for the question provided is 10^4×4^5
If y varies directly as the square root of r and inversely as z cubed, and y = 2.5 when * = 16 and z = 2, find z when x is 64 and y is 0.625.
A. 4
B. 8
C. 16
D. 64
Answers
The value of z when x is 64 and y is 0.625 is 4, which corresponds to option A.
To solve the given problem, we can use the concept of direct and inverse variation.
We are given that y varies directly as the square root of r and inversely as z cubed.
Mathematically, this can be expressed as:
\(y = k \times \sqrt{r / z^3,}\)
where k is the constant of variation.
We are given that y = 2.5 when r = 16 and z = 2.
Let's substitute these values into the equation:
\(2.5 = k \times \sqrt{16 / 2^3, }\)
\(2.5 = k \times 4 / 8,\)
2.5 = k / 2,
\(k = 2.5 \times 2\),
k = 5.
Now we have the value of the constant of variation, k, which is 5.
We are asked to find the value of z when x is 64 and y is 0.625. Let's substitute these values into the equation:
\(0.625 = 5 \times \sqrt{64 / z^3,}\)
\(0.625 = 5 \times 8 / z^3,\)
\(0.625 = 40 / z^3.\)
To solve for z, we can cross-multiply and solve for z:
\(0.625 \times z^3 = 40,\)
\(z^3 = 40 / 0.625,\)
\(z^3 = 64,\)
z = ∛64,
z = 4.
For similar question on inverse variation.
https://brainly.com/question/13998680
#SPJ11