In a two-tailed hypothesis test comparing the means of independent samples, the test statistic is 3.06 and the critical values are /-2.086. True or false: the null hypothesis is not rejected.
Answers
In a two-tailed hypothesis test the null hypothesis is rejected.
According to the statement
The test statistic is 3.06 and the critical values are /-2.086.
If we find the value of t by using the formula the then it comes with Negative sign and it lies under the critical region.
That's why In a two-tailed hypothesis test the null hypothesis is rejected.
Learn more about the HYPOTHESIS here https://brainly.com/question/11555274
#SPJ4
Related Questions
Which of the following is the quotient of the rational expressions shown
below? Make sure your answer is in reduced form.
7x²
3x-5
2x+6 x+3
OA.
OB.
O C.
O D.
O E.
21x³-35x2
2x² +12x+18
7x²
6x-10
7x³ +21x²
6x² +8x-30
6x-10
7x²
6x² +8x-30
7x³+21x²
Answers
The quotient of the rational expressions shown above is given by, Answer: option (C) 7x²/6x-10
To simplify the expression 7x² / 3x-5 / 2x+6 / x+3
We need to perform the following steps:
Invert the divisor.
Change the division to multiplication.
Factor the numerator and denominator.
First, divide the first term in the numerator (7\(x^2\)) by the first term in the denominator (2x) to get 3.
Then multiply (2x + 6) by 3 to get 6x + 18 Subtract this from the numerator.
2x + 6 | 7\(x^2\) + 3x - 5
- (6x + 18)
_______
-3x - 23
Then subtract the following term from the numerator: -3x.
Dividing -3x by 2x gives -3/2.
Multiply (2x + 6) by -3/2. The result is -3x - 9.
Subtract this from the previous result.
3 - (3/2)x
_________
2x + 6 | - 14
The result of polynomial long division is -14.
Therefore, the quotient of the rational expression is (7\(x^2\) + 3x - 5) / (2x + 6) -14.
So the correct answer is option D: -14.
Cancel out any common factors.
Multiply the remaining terms to get the answer.
For more related questions on rational expressions:
https://brainly.com/question/30968604
#SPJ8
A certain radionuclide is used to diagnose lymphoma. an atom of this radionuclide contains 31 protons and 36 neutrons. which statement is correct about the radionuclide? the atomic number is 31, the mass number is 67, and its symbol is superscript 67 subscript 31 baseline upper g a. the atomic number is 31, the mass number is 67, and its symbol is superscript 31 subscript 67 baseline upper g a. the atomic number is 67, the mass number is 31, and its symbol is superscript 67 subscript 31 baseline upper g a. the atomic number is 67, the mass number is 31, and its symbol is superscript 31 subscript 67 baseline upper g a.
Answers
The statement is correct about the radionuclide the atomic number is 31, the mass number is 67, and its symbol is superscript 67 subscript 31 baseline upper g a.
To answert the question, we need to know what an atom is.
What is an atom?An atom is the smallest indivisible part of a substance. It is represented by letters.
It has an atomic number which is the number of protons or electrons present in an atom and is written as a subscript in from of the letter symbol.It has a mass number which is the number of protons plus neutrons in an atom and is written as a subscript in from of the letter symbol.So, since the atom of this radionuclide contains 31 protons and 36 neutrons.
So, its atomic number is 31. Its mass number is number of protons + number of neutrons = 31 + 36 = 67. Its symbol is superscript 67 and subscript 31.
So, the statement is correct about the radionuclide the atomic number is 31, the mass number is 67, and its symbol is superscript 67 subscript 31 baseline upper g a.
Learn more about atom here:
https://brainly.com/question/1805828
#SPJ4
b2+4
when b =3
help me please !!!!
Answers
Answer:
10
Step-by-step explanation:
P.s. Coefficient always goes before the variable
= 2b + 4
= 2(3) + 4 Substitute b for 3
= 6 + 4
= 10
5g(x)=−x−5, find g(5)g(5)
Answers
Step-by-step explanation:
The solution is detailed...
Check it out

Find the percentile for the data point. 4) Data set: 124 136 128 122 130 132 122 120 127 124 128 138 120 124 126 121; data point 130 (Percentile ranking) A) 75 B) 85 C) 70 D) 62
Answers
The closest match to the calculated percentile ranking of 62.5% is option D) 62. Therefore, the correct answer for the percentile ranking of the data point 130 is D) 62.
The given dataset is: 124, 136, 128, 122, 130, 132, 122, 120, 127, 124, 128, 138, 120, 124, 126, 121. We are interested in finding the percentile ranking for the data point 130.
To determine the percentile ranking, we need to count the number of data points that are less than or equal to 130. In this case, there are 10 data points that meet this criterion: 124, 128, 122, 130, 122, 120, 127, 124, 128, 124.
The percentile is then calculated by dividing the number of data points less than or equal to the given value (10) by the total number of data points (16) and multiplying by 100. The percentile ranking for 130 is (10/16) * 100 = 62.5%.
Among the provided options, the closest match to the calculated percentile ranking of 62.5% is option D) 62. Therefore, the correct answer for the percentile ranking of the data point 130 is D) 62.
Learn more about percentile ranking here:
https://brainly.com/question/10684835
#SPJ11
please help:
given CDEF∼GHJK, find CF

Answers
Step-by-step explanation:
Set up a ratio
EF is to JK as CF is to GK
60/40 = CF/38
then 38 * 60/40 = CF = 57 units
WILL GIVE YOU 50 POINT
Find M AFE.
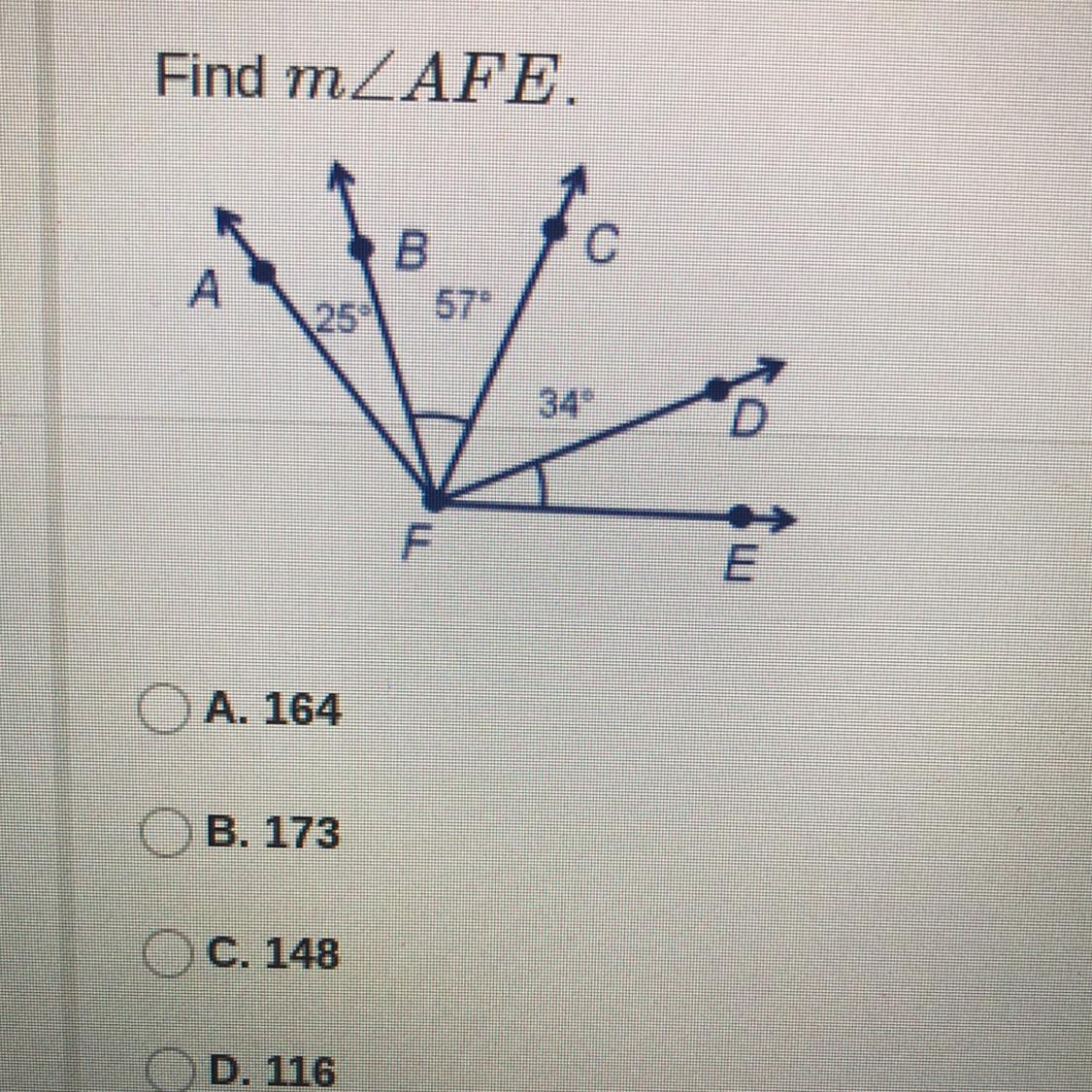
Answers
Answer:
The answer is C
Step-by-step explanation:
25 + 57 + 34 = 116, so at least 116, not 116.
The angle is close to 90+45 = 135
assuming with this, the asnwer is C
Answer:
B. 173
Step-by-step explanation:
just add them all up! for DFE, BFC has the same sign, which i assume means it is the same thing
what is the GCF of 360 &600
Answers
Answer:
120
Step-by-step explanation:
betwenn 360 & 600, 120 is the greatest common factor
What is the equation of the line through the points (1,1), (5,4) (9,7) and (13,10)

Answers
Answer:
Step-by-step explanation:

The equation of the line that passes through (1, 1) and (13, 10) will be y = (3/4)x + 1/4. Then the correct option is D.
What is a linear equation?An association between various factors brings about a direct model when a diagram is shown. The variable will have a level of one.
The linear equation is given as,
y = mx + c
Where m is the slant of the line and c is the y-block of the line.
The equation of the line is passing through (1, 1) and (13, 10). Then the equation of the line is given as,
(y - 1) = [(10 - 1) / (13 - 1)](x - 1)
Simplify the equation in slope-intercept form, then we have
(y - 1) = [(10 - 1) / (13 - 1)](x - 1)
y - 1 = (9 / 12)(x - 1)
y - 1 = (3/4)(x - 1)
y = (3/4)x + 1 - 3/4
y = (3/4)x + 1/4
The condition of the line that goes through (1, 1) and (13, 10) will be y = (3/4)x + 1/4. Then, at that point, the right choice is D.
More about the linear equation link is given below.
https://brainly.com/question/11897796
#SPJ2
Is 313756 divisible by 9?
Answers
Answer:
No.
Step-by-step explanation:
313756 is not divisible by 9 .
Easy way to find it out. - 313756
3+1+3+7+5+6 = 25
25 is not divisible by 3...so , it is not divisible by 9 too
Hope it helps you
Determine the correct classification for each number or expression.

Answers
The numbers in this problem are classified as follows:
π/3 -> Irrational.Square root of 54 -> Irrational.5 x (-0.3) -> Rational.4.3(3 repeating) + 7 -> Rational.What are rational and irrational numbers?Rational numbers are defined as numbers that can be represented by a ratio of two integers, which is in fact a fraction, and examples are numbers that have no decimal parts, or numbers in which the decimal parts are terminating or repeating. Examples are integers, fractions and mixed numbers.Irrational numbers are defined as numbers that cannot be represented by a ratio of two integers, meaning that they cannot be represented by fractions. They are non-terminating and non-repeating decimals, such as non-exact square roots.More can be learned about rational and irrational numbers at brainly.com/question/5186493
#SPJ1
which number is not a perfect square 1) 3 25 81 100 121 2) 4 12 9 144 36 3) 1 16 27 49 64
Answers
Answer:
1. 3
2. 12
3. 27
Step-by-step explanation:
Answer:
1. 3 2. 12 3. 27
Step-by-step explanation:
1. 25's perfect square would be 5. 81's would be 9. 100's is 10. 121's is 11. So therefore, that would leave you with 3.
2. 4's is 2. 9's is 3. 144 is 12. 36 is 6. Therefore, 12 is not a perfect square.
3. The perfect square of 1 is obviously 1. 16 is 4, 49 is 7, and 64 is 8. So, 27 is the odd one out.
I really hope this helped! Good luck :)
5х^2= 10X this is a quadratic
Answers
4. How do you find the slope between two points? Give an example with your explanation

Answers
calculatedThe slope between any two points can be calculated by dividing the change in y by the respective change in x value.
\(\text{slope = }\frac{\text{change in y}}{\text{change in x}}\)\(\begin{gathered} \text{Suppose the two points are given to be points (x}_1,y_1)and(x_2,y_2) \\ \text{Then the slope will be }\frac{y_2-y_1}{x_2-x_1} \end{gathered}\)Example
To calculate the slope of the line joining the points (1,2) and (3,4):
\(\begin{gathered} x_1=1,y_1=2 \\ x_2=3,y_2=4 \\ \text{Slope = }\frac{4-2}{3-1} \\ \text{slope = }\frac{2}{2} \\ \text{slope = 1} \end{gathered}\)Letf(x, y) = 2ex − y.Find the equation for the tangent plane to the graph of f at the point
Answers
The final equation for the tangent plane to the graph of f at the point (a, b) is z = 2e^a(x - a) - y + 2e^a - 2b. This equation represents the plane that is tangent to the graph of f at the specified point (a, b).
To find the equation for the tangent plane to the graph of the function f(x, y) = 2e^x - y at a given point (x0, y0), we need to calculate the partial derivatives of f with respect to x and y at that point.
The partial derivative of f with respect to x, denoted as ∂f/∂x or fₓ, represents the rate of change of f with respect to x while keeping y constant. Similarly, the partial derivative of f with respect to y, denoted as ∂f/∂y or fᵧ, represents the rate of change of f with respect to y while keeping x constant.
Let's calculate these partial derivatives:
fₓ = d/dx(2e^x - y) = 2e^x
fᵧ = d/dy(2e^x - y) = -1
Now, we have the partial derivatives evaluated at the point (x0, y0). Let's assume our point of interest is (a, b), where a = x0 and b = y0.
At the point (a, b), the equation for the tangent plane is given by:
z - f(a, b) = fₓ(a, b)(x - a) + fᵧ(a, b)(y - b)
Substituting fₓ(a, b) = 2e^a and fᵧ(a, b) = -1, we have:
z - f(a, b) = 2e^a(x - a) - (y - b)
Now, let's substitute f(a, b) = 2e^a - b:
z - (2e^a - b) = 2e^a(x - a) - (y - b)
Rearranging and simplifying:
z = 2e^a(x - a) - (y - b) + 2e^a - b
The final equation for the tangent plane to the graph of f at the point (a, b) is z = 2e^a(x - a) - y + 2e^a - 2b.
This equation represents the plane that is tangent to the graph of f at the specified point (a, b).
Learn more about tangent here:
https://brainly.com/question/10053881
#SPJ11
GUYS HELP I GOT TOO MUCH TO DO CAN YOU DO ME A SOLID

Answers
Answer:
2 radical 13
Step-by-step explanation:

Answer:
Answer is C
Step-by-step explanation:
JUST trust my gut
Please, help me with these MATH questions. TRANSFORMATIONS


Answers
3. If triangle ABC was reflected over the x-axis, what would be the coordinate of B'?
When you reflect over the x-axis, you will flip the sign for the y-coordinate. If you reflect over the y-axis, you will flip the sign for the x-coordinate.
In this case, you are reflecting point B (4 , 3) over the x-axis, which will flip the x-coordinate sign to B' (-4 , 3)
D) (-4 , 3)
2. Rotate this figure 270 degrees clockwise
Clock-wise mean you are rotating turning right. 180° is half way, and so it will be D), as 180° is the 3rd option, and then a extra 90° will become D).
Answer:
(4, -3)
last option
Step-by-step explanation:
If a point is reflected over the x-axis then (x, y) → (x, -y)
B = (4, 3)
Therefore, B' = (4, -3)
The original arrowhead is pointing south (down).
If the arrowhead is rotated 270° clockwise, then it will point to the east (right). So the solution is the last option.
savannah recorded the grade level and instrument of everyone in the middle school of rock below guitar 5 bass 12 drums 14 keyboard 4 guitar 12 bass 5 drums 10 keyboard 8

Answers
If a student was randomly chosen from the middle school of rock, there is a 20% chance that they would be playing the drums.
What is probability?Probability is calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
The probability that a student chosen at random will play the drums can be calculated by dividing the total number of drum players by the total number of students in both grade levels.
For this calculation, we will consider the total number of students in both grades, which is 70 (5+12+14+4+12+5+10+8).
Therefore, the probability of a student chosen at random playing the drums can be calculated as follows:
(14 Drum Players/70 Total Students) x 100 = 20%
Rounded to the nearest whole number, the probability of a student chosen at random playing the drums is 20%.
This means that if a student was randomly chosen from the middle school of rock, there is a 20% chance that they would be playing the drums.
For more questions related to whole number
https://brainly.com/question/9879870
#SPJ1
what is the effect on the graph of the function f(x) = |x| when f(x) is changed to ⅔f(x)? A) stretched vertically B) compressed vertically C) stretched horizontally D) compressed horizontally
Answers
Answer: compressed horizontally
Step-by-step explanation:
A beam is subjected to a moment of 786 k-ft. If the material the beam is made out of has a yield stress of 46ksi, what is the required section modulus for the beam to support the moment. Use elastic beam design principles. Submit your answer in in^3 with 2 decimal places.
Answers
The required section modulus for the beam to support the moment of 786 k-ft with a yield of the stress of 46ksi is around 204.87 \(in^3\).
For the calculation of the section modulus for the beam to support the moment given, let's use the elastic beam design principles.
The required formula is:
\(S = M/ f\)
S = required section modulus
M = moment
f = yield stress of the material
The known values are
M = 786 k-ft
f = 46 ksi
We need to convert the units from k-ft to standard form in-lb.
As we know
1 k-ft = 12,000 in-lb
So required unit of M = 786 k-ft × 12,000 in-lb = 9,432,000 in-lb
Let's now calculate the required section modulus:
\(S = M/f\) = 9,432,000 in-lb/ 46 ksi
We will need to convert the kips per square unit from cubic inches to square inches.
\(1in^3 = 1/12 ft^3\)
\(= 1/12 *12^2 = 1/12 ft^2\)
= 1/12 \(in^2\)
S = 9,432,000 in-lb / 46,000 psi
S = 204.87 \(in^3\).
Learn more about modulus from the given link:
https://brainly.com/question/32572508
#SPJ4
Mario and Carlos, two brothers, play for the same basketball team. Here are the points they scored in 10 games:
Answers
The highest point scored is by Carlos with 19 points. Mario's highest was 15. so, Carlos scored 4 points more than Mario.
In the 7th game, Carlos scored 19 points which is the highest point of his game. In the 1st game, Mario scored 15 points which was the highest point he scored. Therefore, Carlos had the highest scoring game between the two of them. Carlos scored 4 points more than Mario did in his highest-scoring game. You can also construct a box plot for this question which will help you visualise this better. The box plot can be made by drawing a number line and marking the following points: minimum, first quartile, median, third quartile and maximum.
Learn more about point scored here:
https://brainly.com/question/29254964
#SPJ4
The full question is:
Mario and Carlos, two brothers, play for the same basketball team. Here are the
points they scored in 10 games:
Game 1 2 3 4 5 6 7 8 9 10
Mario 15 X X 12 7 11 12 11 10 11
Carlos 10 X 9 12 15 X 19 11 12 12
(Xs mark games each one missed.) Which brother had the
highest-scoring game? How many more points did he score in
that game than the other brother did in his highest-scoring game?
I need help finding number 16!!! Quick I don’t know how to find.

Answers
Answer:
17°
Step-by-step explanation:
m∠1 = m∠2.
Set the expressions for 1 and 2 equal to each other.
6x + 5 = 9x - 46
Separate x's on one side.
3x = 51
x = 17
6x + 5 = 9x - 46
6x - 9x = -46 - 5
-3x = -51
x = 17°
Answer: m Angle 1 and m Angle 2 = 17°
what is the exponential function for the graph passing through (-2,1) and (-1,2)
Answers
Answer:
An exponential function has the form `f(x) = ab^x`, where `a` and `b` are constants. To find the exponential function that passes through the points `(-2,1)` and `(-1,2)`, we can use these points to set up a system of equations to solve for the values of `a` and `b`.
Substituting the coordinates of the first point into the equation for an exponential function gives us:
`1 = ab^(-2)`
Substituting the coordinates of the second point into the equation for an exponential function gives us:
`2 = ab^(-1)`
Dividing these two equations gives us:
`(2)/(1) = (ab^(-1))/(ab^(-2))`
`2 = b`
Now that we know that `b=2`, we can substitute this value back into either equation to solve for `a`. Substituting into the first equation gives us:
`1 = a(2)^(-2)`
`1 = a(1/4)`
`a = 4`
So, the exponential function that passes through the points `(-2, 1)` and `(-1, 2)` is given by:
`f(x) = 4 * 2^x`.
To find the exponential function for the graph passing through (-2,1) and (-1,2), we need to use the general form of an exponential function, which is:
y = a * b^x
where:
a is the initial value or the y-intercept of the function
b is the base of the exponential function
x is the variable or the exponent
To determine the values of a and b, we need to use the two given points and solve for the corresponding equations. Substituting the first point (-2,1), we get:
1 = a * b^(-2)
Substituting the second point (-1,2), we get:
2 = a * b^(-1)
Now, we can solve for a and b by eliminating one variable. Dividing the second equation by the first equation, we get:
2/1 = a * b^(-1) / (a * b^(-2))
2 = b
Substituting this value of b into the first equation, we get:
1 = a * 2^(-2)
a = 4
Therefore, the exponential function that passes through (-2,1) and (-1,2) is:
y = 4 * 2^x
or
f(x) = 4 * 2^x
just answer this quistion

Answers
Answer:
5
Step-by-step explanation:
ty
]
find the largest value of $n$ such that $5x^2 nx 48$ can be factored as the product of two linear factors with integer coefficients.
Answers
If we can write
\(5x^2 + nx + 48 = (ax + b) (cx + d)\)
then expanding the right side gives
\(5x^2 + nx + 48 = acx^2 + (ad+bc)x + bd\)
so that \(ac=5\), \(ad+bc=n\), and \(bd=48\), where \(a,b,c,d\) are integers. We want to maximize \(ad+bc\).
5 is prime, so \((a,c)\) can be either (1, 5) or (5, 1). Let \(a=5\) and \(b=1\). Then maximizing
\(ad+bc=5d + c\)
is just a matter of picking the largest possible value for \(d\), which is 48. Then \(\max\{ad+bc\}=5\times48+1\times1=\boxed{241}\).
An economy size car can travel 32 miles for each gallon of gasoline. The function d(g) = 32g represents the distance traveled in miles, d(g), that the car can travel with g gallons of gasoline. Find d(30).
*Type in your answer.
d(30) = miles
Answers
The number of miles to drive for 30 gallons is 960 miles
How to determine the function value?From the question, the function definition is given as
d(g) = 32g
Where g represents the number of gallons and d represents the distance
The function value to calculate is given as
d(30)
This means that we calculate the number of miles to drive for 30 gallons
So, we have
d(30) = 32(30)
This gives
d(30) = 32 x 30
Evaluate the product
d(30) = 960
Hence, the function value is d(30) = 960
Read more about functions at
https://brainly.com/question/28532394
#SPJ1
a survey asks a simple random sample of 500 adults in ohio if they support an increase in the state sales tax from 5% to 6%, with the additional revenue going to education. let denote the proportion in the sample who say they support the increase. suppose that 53% of all adults in ohio support the increase. what is the probability that less than half the sample will say they support the increase? use your calculator. do not round any answer until your final answer. that answer should be rounded to exactly 3 decimal places.
Answers
The probability that less than half of the sample will say that they support the increase is given as follows:
0.0885 = 8.85%.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution, depending if the obtained z-score is positive or negative.Using the z-score table, the p-value associated with the calculated z-score is found, and it represents the percentile of the measure X in the distribution.By the Central Limit Theorem, for a proportion p in a sample of size n, the sampling distribution of sample proportion is approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1 - p)}{n}}\), as long as \(np \geq 10\) and \(n(1 - p) \geq 10\).The parameters for this problem are given as follows:
n = 500, p = 0.53.
Hence the mean and the standard error are given as follows:
\(\mu = 0.53\)\(s = \sqrt{\frac{0.53(0.47)}{500}} = 0.0223\)Hence the probability of less than half is the p-value of Z when X = 0.5, hence:
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
Z = (0.5 - 0.53)/0.0223
Z = -1.35
Z = -1.35 has a p-value of 0.0885.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
Which function in vertex form is equivalent to f(x) = x2 + 8 – 16x? f(x) = (x – 8)2 – 56 f(x) = (x – 4)2 + 0 f(x) = (x + 8)2 – 72 f(x) = (x + 4)2 – 32
Answers
Answer:
f(x) = x² + 8 - 16x
= x² - 16x + 8
= (x² - 16x + 64) - 64 + 8
= (x - 8)² - 56
Answer:
A. f(x) = (x – 8)2 – 56
Step-by-step explanation:
so much for expert verified, huh.. -_-
What is the missing step in solving the inequality 4(x – 3) + 4 < 10 + 6x?
1. The distributive property: 4x – 12 + 4 < 10 + 6x
2. Combine like terms: 4x – 8 < 10 + 6x
3. The addition property of inequality: 4x < 18 + 6x
4. The subtraction property of inequality: –2x < 18
5. The division property of inequality: ________
x < –9
x > –9
x < x is less than or equal to negative StartFraction 1 Over 9 EndFraction.
x > –x is greater than or equal to negative StartFraction 1 Over 9 EndFraction.
Answers
The missing step in solving the inequality 4(x – 3) + 4 < 10 + 6x is step 6: The division property of inequality: x > -9
How to find the missing stepThe missing step in solving the inequality 4(x – 3) + 4 < 10 + 6x is step 6: The division property of inequality.
After step 4, which is -2x < 18, we need to divide both sides of the inequality by -2 to solve for x.
However, since we are dividing by a negative number, the direction of the inequality sign needs to be reversed.
Dividing both sides by -2:
-2x / -2 > 18 / -2
This simplifies to:
x > -9
Therefore, the correct answer is x > -9.
Learn more about inequality at https://brainly.com/question/25275758
#SPJ1
the early income of a girl is rupees 150000 the tax free allowance is rupees 100000 if the text for the first rupees 20000 is 12% and for the remaining is 15% how much tax should she pay in a year ?
Answers
Answer:
Rs 6900
Step-by-step explanation:
To calculate the tax amount the girl should pay in a year, we need to determine the taxable income and then apply the corresponding tax rates.
The taxable income is calculated by subtracting the tax-free allowance from the girl's early income:
Taxable Income = Early Income - Tax-Free Allowance
Taxable Income = 150,000 - 100,000
Taxable Income = 50,000
Now, we can calculate the tax amount based on the given tax rates:
For the first 20,000 rupees, the tax rate is 12%:
Tax on First 20,000 = 20,000 * 0.12
Tax on First 20,000 = 2,400
For the remaining taxable income (30,000 rupees), the tax rate is 15%:
Tax on Remaining 30,000 = 30,000 * 0.15
Tax on Remaining 30,000 = 4,500
Finally, we add the two tax amounts to get the total tax she should pay in a year:
Total Tax = Tax on First 20,000 + Tax on Remaining 30,000
Total Tax = 2,400 + 4,500
Total Tax = 6,900
Therefore, the girl should pay 6,900 rupees in tax in a year.