If the cost of 9 m cloth is rupees 378, find the cost of 4 m cloth? guys little fast and please in steps no direct answers
Answers
Answer: 168 rupees.
Step-by-step explanation:
sure thing! first, i divided 378 by 9, so that i could find the cost of ONE meter of cloth.
378/9 = 42
then, i just multiplied 42 by 4, in order to find the total cost for 4 meters.
42 x 4 = 168
Related Questions
Please help!!
What is the value of the expression
?(2^4)^2
Answers
Answer:256
Step-by-step explanation:
What are the solutions to the equation (10−x)(3x−9)=0?
Answers
Answer:
10−x)(3x−9)=0
−3x2+39x−90=0
−3(x−3)(x−10)=0
x=3 or x=10
The solutions to the equation (10 - x)(3x - 9) = 0 are x = 10 and x = 3.
Given that the equation (10 - x)(3x - 9) = 0
The factors will have the form (ax + b)(cx + d), where a, b, c, and d are constants.
To find values for a, b, c, and d such that (ax + b)(cx + d) is equal to 0
To determine the solutions of (ax + b)(cx + d), equate each term to zero and solve for x which gives the solutions.
The two solutions of (ax + b)(cx + d) are -b/a and -c/d.
To find the solutions to the equation (10 - x)(3x - 9) = 0, set each factor equal to zero and solve for x.
Setting (10 - x) = 0 gives:
10 - x = 0
To isolate x, subtract 10 from both sides of the equation:
10 - x - 10 = 0 - 10
Simplifying gives:
-x = -10
Multiplying both sides by -1 to solve for x:
(-1)(-x) = (-1)(-10)
x = 10
So, one solution is x = 10.
Now, setting (3x - 9) = 0, gives:
3x - 9 = 0
To isolate x, we add 9 to both sides of the equation:
3x - 9 + 9 = 0 + 9
Simplifying gives:
3x = 9
Dividing both sides by 3 to solve for x:
(1/3)(3x) = (1/3)(9)
x = 3
Therefore, the second solution is x = 3.
The solutions to the equation (10 - x)(3x - 9) = 0 are x = 10 and x = 3.
Learn more about solving quadratic equations and factoring, click here:
https://brainly.com/question/30398551
#SPJ6
round to one decimal place. you 3.4 for πFind the area of the sector

Answers
We will determine the area as follows:
\(A=\frac{3}{4}\pi r^2\Rightarrow A=\frac{3}{4}(3.14)(3)^2\)\(\Rightarrow A=21.195\Rightarrow A\approx21.2\)So, the area of the sector is approximately 21.2 square units.
(The reason it is multiplied by 3/4 is that the normal area of a circumference is given by pir^2 [Whole circle], but since it is stated that the missing area has an angle of 90°, then the remainder of the circle [Area to find] is 3/4 of the original are).
What is the area of a rectangle with 5cm height and 77cm length?
Answers
Answer:
area = 385 cm²
Step-by-step explanation:
area = 5cm * 77cm
area = 385 cm²
which of the following actions is a person most likely to take if he or she has a hig level of self-disipline
Answers
Answer:
respect , structure
Step-by-step explanation:
If a person has a high level of self-discipline, that means they are very responsible and self-controlled.
They work hard without being asked to, and they stop themselves from getting addicted to things, and they don't do anything bad.
♡ Hope this helped! ♡
❀ 0ranges ❀
on the island of mumble, the mumblian alphabet has only $5$ letters, and every word in the mumblian language has no more than $3$ letters in it. how many words are possible? (a word can use a letter more than once, but $0$ letters does not count as a wor
Answers
The total number of possible words is 155.
How many words are possible? (A word can use a letter more than once, but 0 letters do not count as a word)
There are 5 letters in the mumblian alphabet, and each word must contain 1, 2, or 3 letters.
The number of 1 letter words is 5 since every letter is a word.
The number of 2 letter words is 5 × 5 = 25 because there are 5 options for the first letter and 5 options for the second letter.
The number of 3 letter words is 5 × 5 × 5 = 125 because there are 5 options for the first letter, 5 options for the second letter, and 5 options for the third letter. Therefore, the total number of possible words is:
\($5 + 25 + 125 = \boxed{155}$\)
To know more about letter words problems: https://brainly.com/question/29424977
#SPJ11
is λ=3 an eigenvalue of 2 0 −1 2 2 3 −4 3 −4 ? if so, find one corresponding eigenvector.
Answers
Thus, we can write that the value of λ=3 is an eigenvalue of the given matrix A and the corresponding eigenvector is v=[-2 5 1]T.
Given matrix is:\($$A = \begin {bmatrix} 2 & 0 & -1 \\ 2 & 2 & 3 \\ -4 & 3 & -4 \end {bmatrix}$$\)Now, to check whether λ = 3 is an eigenvalue of the given matrix A, we will find the determinant of the matrix (A - λI), where I is the identity matrix. If the determinant is zero, then λ is an eigenvalue of the matrix A. The matrix (A - λI) is\(:$$\ {bmatrix} 2 - 3 & 0 & -1 \\ 2 & 2 - 3 & 3 \\ -4 & 3 & -\)end {bmatrix}$$Now, finding the determinant of the above matrix using the cofactor expansion along the first row:$${\begin{aligned}\det(A-\lambda I)&=-1\cdot \begin{vmatrix} -1 & 3 \\ 3 & -7 \end{vmatrix}-0\cdot \begin{vmatrix} 2 & 3 \\ 3 & -7 \end{vmatrix}-1\cdot \begin{vmatrix} 2 & -1 \\ 3 & 3 \end{vmatrix}\\&=-1((1\cdot -7)-(3\cdot 3))-1((2\cdot 3)-(3\cdot -7))\\&=49\end{aligned}}$$Since the determinant is non-zero, hence λ = 3 is an eigenvalue of the matrix A.
Now, to find the corresponding eigenvector, we will solve the equation (A - λI)v = 0, where v is the eigenvector and 0 is the zero vector. The equation becomes:\($$\begin{bmatrix} -1 & 0 & -1 \\ 2 & -1 & 3 \\ -4 & 3 & -7 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}$$$$\Rightarrow -x - z = 0$$$$2x - y + 3z = 0$$$$-4x + 3y - 7z = 0$$\)Solving the above system of equations using substitution method, we get y = 5z and x = -2z. Taking z = 1, we get the eigenvector as\(:$$v = \begin{bmatrix} -2 \\ 5 \\ 1 \end{bmatrix}$$\)Therefore, λ = 3 is an eigenvalue of the given matrix A and the corresponding eigenvector is v = [-2 5 1]T.
To know more about eigenvalue visit:-
https://brainly.com/question/31650198
#SPJ11
7 (n + 4) = 21 Plsss HELP NOW I will try to get u brainliest
Answers
Answer:
n = -1
Step-by-step explanation:
please mark me brainliest
Answer:
n = -1
Step-by-step explanation:
7 (n + 4) = 21
28 + 7n = 21
28 + -28 + 7n = 21 - 28
7n = -7
n = -1
hi ate this here sis at St do do
Answers
Answer:
Hiiiiiiiiiiiiii iiiiiiiiiiiiiiii
help i’ll give brainliest
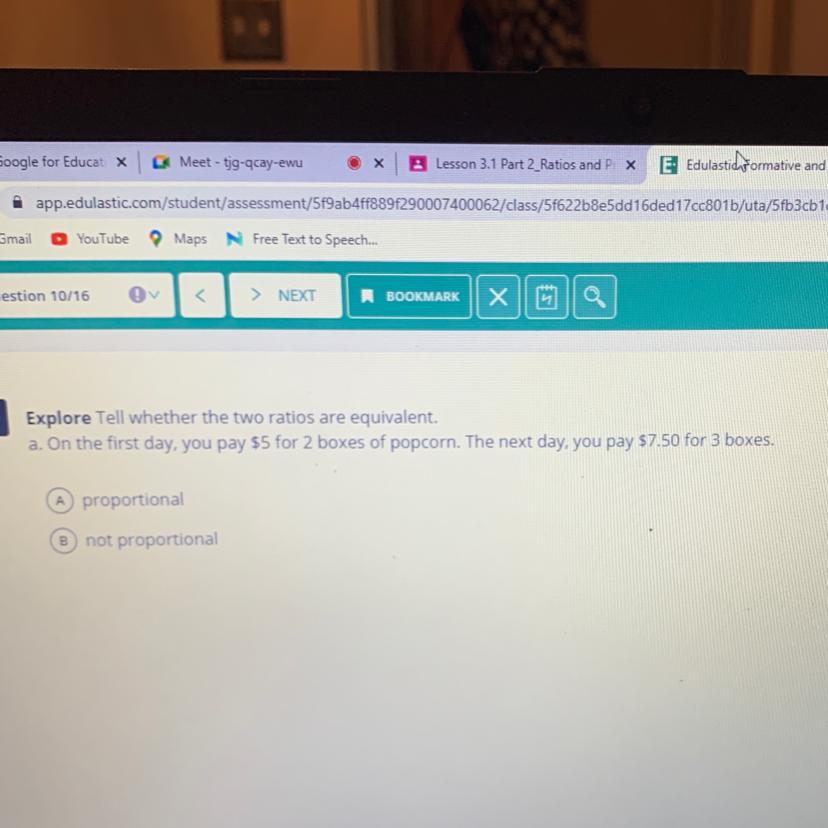
Answers
I think that is proportional
First to answer
Answer:
The answer is proportional! The pricing is consistent!
5/2 = 2.5
2.5* 3 = 7.5
Which are examples of statistical questions?
Question 11
Question 2
Question 3
Question 4
Questions
What is Mikki's favorite time to go to sleep?
What time does each student go to sleep?
What time does Malia wake-up in the morning?
What time does each student wake-up?
O questions 1 and 2
O questions 1 and 3
questions 2 and 4
questions 2 and 3
Answers
Several friends (Calvin, Dean, Kelli, and Lee) went to Cal's Late Night Diner for a bite to eat. Match each person to their drink (Iced tea, Lemonade, Root Beer, and Water) and determine how much each paid ($4.99, $5.99, $6.99, and $7.99) for their meal.
Clues:
1. The Diner who paid $4.99 was either Calvin or the one who got the Root Beer.
2. Kelli paid $6.99
3. The one who got the water paid 1 dollar less than Dean.
4. Calvin paid more than Lee.
5. The one who got the Root beer paid 1 dollar less than the one who got the Iced Tea.
Answers
Based on the given clues, we can determine the person, drink, and price paid for each individual:
Calvin: Root Beer, $4.99
Dean: Lemonade, $7.99
Kelli: Water, $6.99
Lee: Iced Tea, $5.99
How to determine how much each friends paidFrom clue 1, we know that either Calvin or the person who got the Root Beer paid $4.99. Since Calvin paid more than Lee according to clue 4, Calvin cannot be the one who got the Root Beer. Therefore, Calvin paid $4.99.
From clue 2, Kelli paid $6.99.
From clue 3, the person who got the water paid $1 less than Dean. Since Dean paid the highest price, the person who got the water paid $1 less, which means Lee paid $5.99.
From clue 5, the person who got the Root Beer paid $1 less than the person who got the Iced Tea. Since Calvin got the Root Beer, Lee must have gotten the Iced Tea.
Therefore, the final assignments are:
Calvin: Root Beer, $4.99
Dean: Lemonade, $7.99
Kelli: Water, $6.99
Lee: Iced Tea, $5.99
Learn more about word problems at https://brainly.com/question/21405634
#SPJ1
Rachel is stuffing envelopes. She has eight hours to complete the task, and there are 1,500envelopes. The first hour, Rachel stuffs 135 envelopes. The second hour she stuffs 141 envelopes. How many envelopes will Rachel need to stuff in order to finish the job?
Answers
The processes and functions of the body
The processes of the mind
Social needs, social behaviors, and social problems
Otraits that increase the possibility of developing an illness or disease
Check out this cube: The figure presents a cube. The length of one edge is labeled as 3 units The figure presents a cube. The length of one edge is labeled as 3 units Find the surface area of the cube (above) using its net (below). The figure presents a surface net of a cube. The net consists of 4 squares connected in a row. The second square from the left is also connected to a square above it, and a square below it. The length of one side of one square is labeled as 3 units. The figure presents a surface net of a cube. The net consists of 4 squares connected in a row. The second square from the left is also connected to a square above it, and a square below it. The length of one side of one square is labeled as 3 units. units 2 2
Answers
Answer: look it up-
Step-by-step explanation:
What is the range of the data show in the frequency table? Age Tally Frequency 24 | 1 25 || 2 26 5 27 |||| 4 28 0 29 |||| 4 5 3 4 13
Answers
Answer:
The range of the data is 9.
Step-by-step explanation:
The frequency table shown is:
Age Tally Frequency
24 | 1
25 || 2
26 ||||| 5
27 |||| 4
28 - 0
29 |||| 4
30 ||||| 5
31 ||| 3
32 |||| 4
33 13
The range of a data set is the difference between the highest and the lowest value.
Range = Maximum - Minimum
= 33 - 24
= 9
Thus, the range of the data is 9.
Answer:
3
Step-by-step explanation:
leah has 2/5 gallons of paint. she decides to use 1/4 of this paint to paint a door. what fraction of a gallon of paint does she suse for the door
Answers
Leah has 2/5 gallons of paint. She decides to use 1/4 of this paint to
a door. What fraction of a gallon of paint does she use for the door.
To find out what fraction of a gallon of paint Leah uses for the door, we need to multiply the amount of paint she has (2/5 gallons) by the fraction of the paint she uses for the door (1/4).When we multiply two fractions, we multiply the numerators (top numbers) together, and then the denominators (bottom numbers) together. The result is the product of the two fractions, which is also a fraction.
So,Leah uses (2/5) × (1/4) = (2 × 1) / (5 × 4) = 2/20Since 2 and 20 have a common factor of 2, we can simplify this fraction by dividing the numerator and denominator by 2:2/20 = 1/10Therefore, Leah uses 1/10 of a gallon of paint to paint the door. To summarize: Leah uses 1/10 gallon of paint to paint the door.
To know more about paint visit :
https://brainly.com/question/15277377
#SPJ11
(-2,0) and (3,4)
slope=1/3 and (2,4)
SOLVE EQUATIONS FOR THEM PLEASE
Answers
Answer: \(a)\quad y=\dfrac{4}{5}x+\dfrac{8}{5}\) \(b)\quad y=\dfrac{1}{3}x+\dfrac{10}{3}\)
Step-by-step explanation:
Use the Slope formula: \(m=\dfrac{y_2-y_1}{x_2-x_1}\)
and the Point-Slope formula: y - y₁ = m(x - x₁)
a) (-2, 0) and (3, 4)
\(m=\dfrac{0-4}{-2-3}\quad =\dfrac{-4}{-5}\quad =\dfrac{4}{5}\)
Let (x₁, y₁) = (-2, 0)
y - y₁ = m(x - x₁)
\(y-0=\dfrac{4}{5}\bigg(x-(-2)\bigg)\\\\\\y\quad =\dfrac{4}{5}\bigg(x+2\bigg)\\\\\\\large\boxed{y\quad =\dfrac{4}{5}x+\dfrac{8}{5}}\)
b) m = 1/3 (x₁, y₁) = (2, 4)
y - y₁ = m(x - x₁)
\(y-4=\dfrac{1}{3}\bigg(x-2\bigg)\\\\\\y-4 =\dfrac{1}{3}x-\dfrac{2}{3}\\\\\\y\quad \ =\dfrac{1}{3}x-\dfrac{2}{3}+\dfrac{12}{3}\\\\\\\large\boxed{y\quad =\dfrac{1}{3}x+\dfrac{10}{3}}\)
3(x - 2) + 2 = 5(x - 3) + 9 por fa
Answers
Answer:
x = 1
Step-by-step explanation:
Given
3(x - 2) + 2 = 5(x - 3) + 9 ← distribute and simplify both sides
3x - 6 + 2 = 5x - 15 + 9
3x - 4 = 5x - 6 ( subtract 5x from both sides )
- 2x - 4 = - 6 ( add 4 to both sides )
- 2x = - 2 ( divide both sides by - 2 )
x = 1
Question 3 The Schwarzschild metric is given by 2M 2M ds² -(₁-²M) di² + (1-²¹)- 1- dr² +r² (d0² + sin² 0 dó²). There are Killing vectors associated with time invariance and angular momen- tum invariance in the direction in this geometry leading to the conserved quantities e = (1-2) and l= r² sin² 0 dr From this one can derive an analog to the radial energy equation in Newtonian mechanics by orienting the coordinates so that the orbits are confined to the equatorial plane where 0 = π/2 and u = 0. One finds 2 1 dr + Veff (r) = E 2 dr (e²_ -1) where E = and Veft(r) = - + 2/²/²2 - Mp³². Further, for circular orbits one can show that M | [₁ + √/₁−12 (+1)]. r+= | 2M Finally, for circular orbits of radius R do 1/2 M dt R³ (a) Which value of r corresponds to the Schwarzschild radius of stable circular orbits: r or r? Justify your answer. [3 marks] (b) Show that for circular orbits of radius R do 1/2 M -1/2 3M (²) ¹² (1-³) dT R³ R where is the proper time. [6 marks] (c) A free particle is moving in a circular orbit around a spherical source of curvature of mass M. The Schwarzschild radius of the orbit is 8M. Use the equivalence principle to argue that the period as measured at infinity should be larger than that measured by the particle. [4 marks] (d) Find the period of the orbit as measured by an observer at infinity. Find the period of the orbit as measured by the particle. [7 marks] M
Answers
(A) Circular orbits of stable particles are possible at radii greater than three times the Schwarzschild radius for the non-rotating spherically symmetric mass.
This represents the radius of a black hole's event horizon, within which nothing can escape. The Schwarzschild radius is the event horizon radius of a black hole with mass M.
M can be calculated using the formula: r+ = 2Mwhere r+ is the radius of the event horizon.
(B) 1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ R. This is the required expression.
Tau is the proper time of the particle moving around a circular orbit. Hence, by making use of the formula given above:1/2 M -1/2 3M (²) ¹² (1-³) dT = R³ dt.
(C) Time passes differently in different gravitational fields, and it follows that the period as measured at infinity should be larger than that measured by the particle.
The principle of equivalence can be defined as the connection between gravitational forces and the forces we observe in non-inertial frames of reference. It's basically the idea that an accelerating reference frame feels identical to a gravitational force.
(D) The period of the orbit as measured by an observer at infinity is 16π M^(1/2) and the period of the orbit as measured by the particle is 16π M^(1/2)(1 + 9/64 M²).
The period of orbit as measured by an observer at infinity can be calculated using the formula: T = 2π R³/2/√(M). Substitute the given values in the above formula: T = 2π (8M)³/2/√(M)= 16π M^(1/2).The period of the orbit as measured by the particle can be calculated using the formula: T = 2π R/√(1-3M/R).
Substitute the given values in the above formula: T = 2π (8M)/√(1-3M/(8M))= 16π M^(1/2)(1 + 9/64 M²).
To know more about Schwarzschild radius
https://brainly.com/question/29534114
#SPJ11
The price of a trampoline before tax is $300. The salesvtax is 4%
Answers
300 x 1.04 = 312
Answer:
The total price is $312 and the sales tax is 12
Step-by-step explanation:
300 x 0.04= 12
300 + 12 = 312
2. A ladder is leaning against a wall. The base of
the ladder makes a 60° angle with the ground.
The base of the ladder is 17 feet from the wall.
What is the length of the ladder?
Answers
This is a classic example of a right triangle trigonometry problem, where the angle and one of the sides are given and the goal is to find the length of the hypotenuse.
To solve this problem, we can use the trigonometric function of sine, cosine, or tangent to find the length of the ladder.
To solve this problem, we can use the trigonometric function of sine, cosine, or tangent to find the length of the ladder. In this case, we can use the sine function, as we have the opposite side (the height of the triangle, which is the distance from the ground to the point where the ladder is leaning against the wall) and we want to find the hypotenuse (the length of the ladder). The sine of the angle is the ratio of the opposite side to the hypotenuse. Using this formula, we can calculate the length of the ladder by multiplying the height by the reciprocal of the sine of the angle. Therefore, the length of the ladder is 17/sin(60°) or approximately 19.65 feet.
To learn more about triangle trigonometry, click here:
brainly.com/question/15101552
#SPJ11
Brandi completed 7 out of her 9 chores. What percent does she have left to finish?
A. 22%
B. 33%
C. 78%
D. 82%
Answers
Answer: C. 78%
Step-by-step explanation:
simply divide 7 by 9 and move the decimal two places to the right and round!
A playground area is going to be built in a zoo park. The shape of the playground is shown below. This area will be covered with recycled rubber chips. Each unit represents 1 ft. Installing the rubber chips costs $52.50 per square foot. How much will it cost to install the rubber chips?
Answers
Answer:
$2075.75
Step-by-step explanation:
I think your question is missed of key information, allow me to add in and hope it will fit the original one.
Please have a look at the attached photo.
My answer:
Given the information;
rubber chips costs $52.50 per square foot
We need to find the area of the playground,
1. We find the area of the rectangle:The length: 8ft
The width: 4 ft
=> the area of it is: 8*4 = 32 square foot.
2. We find the area of the 1st identical trianglesThe base: 3 ft
The height: 2 ft
=> the area of it is = 1/2*3*2 = 3 square foot.
3. We find the area of the 2nd identical trianglesThe base: 3 ft
The height: 3 ft
=> the area of it is = 1/2*3*3 = 9/2 square foot.
=> the total area of the playground is: 32 + 3 + 9/2 = 39.5 square foot.
So the total cost to install the rubber chips is:
= 39.5 * $52.5
= $2075.75
Hope it will find you well.

The $2625 is the cost to install the rubber chips if each unit represents 1 ft. Installing the rubber chips costs $52.50 per square foot.
What is the area of the rectangle?It is defined as the area occupied by the rectangle in two-dimensional planner geometry.
The area of a rectangle can be calculated using the following formula:
Rectangle area = length x width
First, we find the area of the rectangle = (8+3)×4 = 44 square feet
Area of the two triangle = 2(1/2)[2×3] = 6 square feet
Area of the complete figure = 44+6 = 50 square feet
Each unit represents 1 ft. Installing the rubber chips costs $52.50 per square foot.
Total cost = 50×52.50 = $2625
Thus, the $2625 is the cost to install the rubber chips if each unit represents 1 ft. Installing the rubber chips costs $52.50 per square foot.
Learn more about the rectangle here:
https://brainly.com/question/15019502
#SPJ5
2(3+3g)>12+4m solve each inequality.
Answers
Step-by-step explanation:
\(2(3 + 3g) >12 + 4m \\ 6 + 6g > 12 + 4m \\ 6 - 12 > - 6g + 4m \\ - 6 > - 6g + 4m\)
The slope of the rafter is 15 m.Half the run of the rafter measure 12m.find the height of the ridge from the base

Answers
Answer:
\(9\; \rm m\).
Step-by-step explanation:
Assume that the run of this rafter is level. Then the height of the ridge (the line with a question mark next to it in the diagram) should be perpendicular to the line marked with \(\rm 12\; m\). The three labelled lines in this diagram will form a right triangle.
The line marked as \(15\; \rm m\) will be the hypotenuse of this right triangle.The line marked as \(12\; \rm m\) will be one of the triangle's legs.The line representing the height of the ridge (the one with the question mark) will be the other leg of this right triangle.Hence, the height of this ridge can be found with the Pythagorean Theorem. By the Pythagorean Theorem:
\((\text{First Leg})^2 + (\text{Second Leg})^2 = (\text{Hypotenuse})^2\).
In this particular right triangle:
\((\text{Height})^2 + (12\; \rm m)^2 = (15\; \rm m)^2\).
\((\text{Height})^2 = (15\; \rm m)^2 - (12\; \rm m)^2\).
Therefore, the height of this ridge would be \(\sqrt{81}\; \rm m = 9\; \rm m\). (Note the unit.)
Two trains leave the city going opposite directions, one going north and the other going south. The northbound train is traveling 14 mph slower than the southbound train. After 3 hours the trains are 498 miles apart. Find the speed of each train
Answers
Let the speed of the southbound train be x mph. then the speed of the northbound train will be x - 14 mph.
Both trains are traveling in the opposite direction and going away from each other.
The distance traveled by southbound train in 3 hours will be 3x miles. The distance traveled by southbound train will be 3(x - 14) miles.
Therefore, the sum of distance covered by both the trains will be equal to 498 miles.
\(\begin{gathered} 3x+3(x-14)=498 \\ 3x+3x-42=498 \\ 6x-42=498 \\ 6x-42+42=498+42 \\ 6x=540 \\ x=90 \end{gathered}\)Thus, the speed of the southbound train is 90 mph and the speed of the northbound train is 76 mph.
one cell phone plan charges a flat monthly rate of $49.99 with extra charges of $0.10 per text message after the first 100 text messages. (a) choose letters that best represent the variables needed to write a formula that expresses the cell phone charges. let t denote the number of text messages. let t denote the number of text messages and c the charge, in dollars. let t denote the number of text messages, p the type of plan, and c the charge, in dollars. let c denote the charge, in dollars. correct: your answer is correct. (b) write a formula to express the cell phone charges as a function of the number of text messages (assume that the number is at least 100). c
Answers
(a) is: Let t denote the number of text messages and c the charge, in dollars, (b) The formula is c(t) = 49.99 + 0.10(t - 100).
(a) In this case, we will let t denote the number of text messages and c represent the charge, in dollars.
(b) To write a formula for the cell phone charges as a function of the number of text messages (assuming t is at least 100), we will consider the flat monthly rate of $49.99 and the extra charges of $0.10 per text message after the first 100 messages. The formula will be:
c(t) = 49.99 + 0.10(t - 100)
This formula calculates the total charge, c(t), based on the number of text messages, t. The first 100 text messages are included in the flat monthly rate of $49.99, so we subtract 100 from the total number of text messages, t, and multiply the result by the extra charge per text message, $0.10. Then we add the flat monthly rate of $49.99 to get the total charge, c(t).
To learn more about function: https://brainly.com/question/22340031
#SPJ11
what is 1 and 2/5 as an improper fraction
Answers
Answer:
\(\displaystyle 1\frac{2}{5}=\frac{7}{5}\)
Step-by-step explanation:
\(\displaystyle a\frac{b}{c}=\frac{ac+b}{c}\\\\1\frac{2}{5}=\frac{(1)(5)+2}{5}=\frac{5+2}{5}=\frac{7}{5}\)
Alejandra correctly wrote the equation y - 3 = (x - 10) to represent a line that her teacher sketched. The teacher then
changed the line so it had a slope of 2, but still went through the same point. Which equation should Alejandra write to represent
the new line?
O y-6 = 2(x - 10)
Oy-2 = 5(x - 10)
Oy-3 = {(x-2)
Oy-3 = 2(x - 10)
Answers
Kimberly is admiring a statue in Newberry Park from 4 meters away. If the distance between the top of the statue to Kimberly's head is 9 meters, how much taller is the statue than Kimberly? If necessary, round to the nearest tenth.
Answers
The statue is about 9.8 - 1.5 = 8.3 meters taller than Kimberly.
What is height?
Height typically refers to the measurement of how tall or high something or someone is, usually measured from the ground or a given baseline. It is often used as a physical descriptor of an object or person, and can be measured in various units such as feet, meters, or inches. Height can also be used to describe the vertical extent or distance of an object or structure, such as the height of a building or the height of a mountain.
We can use the Pythagorean theorem to solve the problem.
Let h be the height of the statue. Then, we have:
h² = 4² + 9²
h² = 16 + 81
h² = 97
h ≈ 9.8
Therefore, the statue is about 9.8 - 1.5 = 8.3 meters taller than Kimberly.
To learn more about height, visit the link:
https://brainly.com/question/28122539
#SPJ1