If ABCD is a parallelogram. BC=13 and AB=5, what is the perimeter of the parallelogram?
Answers
Answer:
36
Step-by-step explanation:
In a Parallelogram , it is important to note that opposite sides are equal to each other.
We are given parallelogram ABCD.
We have sides: AB, BC, CD, AD.
Since opposite sides are equal then:
AB = CD
BC = AD
The perimeter of a parallelogram is the sum of all its sides.
In the question: BC=13 and AB=5
Hence,
AB = CD = 5
BC = AD = 13
Perimeter of Parallelogram ABCD = 5 + 5 + 13 + 13
= 36.
Related Questions
the measure of angle ABX is 4x-16 and the measure of CBX is 2x+6 what is x and then find the measure of angle ABC

Answers
Answer:
The values of x and angle ABC are;
\(\begin{gathered} x=11 \\ \measuredangle ABC=56^0 \end{gathered}\)Explanation:
From the instruction above;
Line BX bisects angle ABC.
So;
\(\measuredangle ABX=\measuredangle CBX\)Given;
\(\begin{gathered} \measuredangle ABX=4x-16 \\ \measuredangle CBX=2x+6 \end{gathered}\)Substituting this values, we have;
\(\begin{gathered} \measuredangle ABX=\measuredangle CBX \\ 4x-16=2x+6 \end{gathered}\)Then we can solve for x; collecting the like terms
\(\begin{gathered} 4x-2x=6+16 \\ 2x=22 \\ x=\frac{22}{2} \\ x=11 \end{gathered}\)Then we can now solve for angle ABC;
Since line BX bisect angle ABC, Angle ABC equal 2 times angle ABX;
\(\begin{gathered} \measuredangle ABC=2(\measuredangle ABX) \\ \measuredangle ABC=2(4x-16) \\ \measuredangle ABC=8x-32 \\ \text{ since x=}11 \\ \measuredangle ABC=8(11)-32 \\ \measuredangle ABC=88-32 \\ \measuredangle ABC=56^0 \end{gathered}\)Therefore, the values of x and angle ABC are;
\(\begin{gathered} x=11 \\ \measuredangle ABC=56^0 \end{gathered}\)Please help!! Will give brainliest if correct!
If triangle RST is an equilateral triangle, find x and y.
A. x = 70, y = 35
B. x = 80, y = 40
C. x = 120, y = 30
D. x = 120, y = 40

Answers
Answer:
C.
Step-by-step explanation:
Out of 300 people how many say fall is favorite season
Answers
Answer:Compare this experimental probability to the population probability that fall is the favorite season. a. Out of 300 people, 4 people would say that fall is their favorite season.
Step-by-step explanation:
Find all the missing values to make the equation true

Answers
The missing value in the logarithm are as follows:
log₃ 7 - log₃ 2 = log₃ (7 / 2)log₉ 7 + log₉ 4 = log₉ 28log₆ 1 / 81 = - 4 log₆ 3How to solve logarithm?Using logarithm rule,
logₐ b - logₐ c = logₐ (b / c)
logₐ b + logₐ c = logₐ (b × c)
Therefore,
log₃ 7 - log₃ 2 = log₃ (7 / 2)
log₉ 7 + log₉ 4 = log₉ (7 × 4) = log₉ 28
log₆ 1 / 81 = log₆ 81⁻¹ = log₆ 3⁻⁴ = - 4 log₆ 3
learn more on logarithm here: brainly.com/question/24515212
#SPJ1
HELP! Will be giving extra points and branliest!!
Please give an explanation if possible

Answers
Answer:
B-6 1/4
Step-by-step explanation:
You take 1,250 and divided by 50 because that you base you should get 25. You then Take 1/4 and turn it into a decimal .25, then you times .25 by 25 and get 6.25. All you do after that is make it a fraction of 6 1/4 and you have your answer.
Can anyone help me on this one

Answers
Hello !
Answer :
\({x}^{ - \frac{8}{3} }\)\(\sqrt[3]{ {x}^{ - 8} }\)\(\sqrt[3]{ ({x}^{ 4}) {}^{ - 2} }\)Explanation :
\( \to \boxed{ ({x}^{a}) {}^{b} = {x}^{ab} } \)
\( \to \boxed{ {x}^{ \frac{1}{n} } {}^{} = \sqrt[n]{x} } \)
\( ({x}^{4} ) {}^{ - \frac{2}{3} } = {x}^{- \frac{2}{3} \times 4} \\ \boxed{= {x}^{ - \frac{8}{3} } } \\ \boxed{= \sqrt[3]{ {x}^{ - 8} }} \\ \boxed{ = \sqrt[3]{ ({x}^{ 4}) {}^{ - 2} }}\)
Have a nice day ;)
What is the solution to this equation? 5x+3=2x−6 Enter your answer in the box.
Answers
Answer:
x=−3
Step-by-step explanation:
you manage a restaurant and need to replace a broken dishwasher
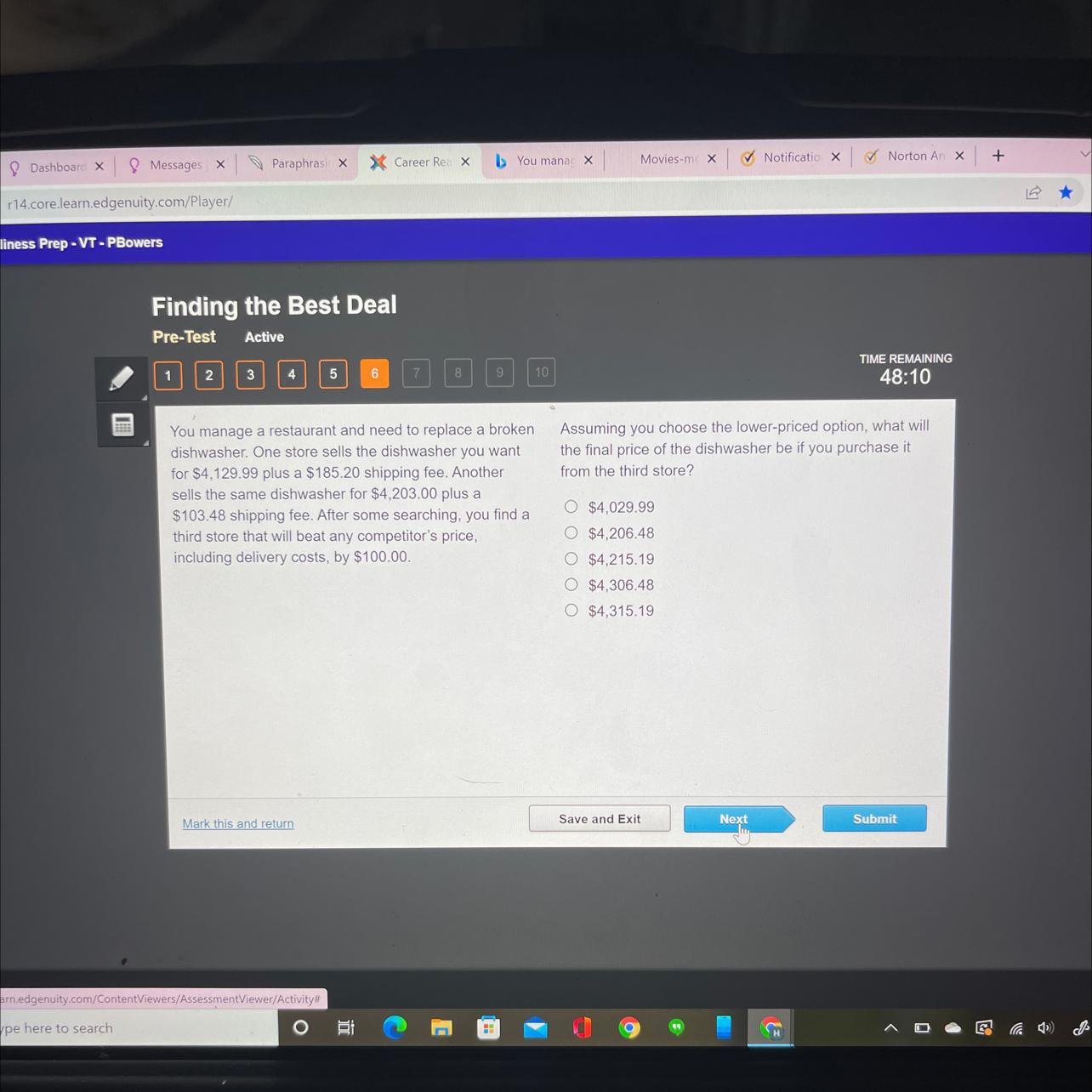
Answers
Answer:
B
Step-by-step explanation:
Paula caught a tarpon with a weight that was 11 times as great as the weight of a permit fish she caught
The total weight of the two fish was 132 pounds.
How much did each fish weigh?
Answers
Let one fish weigh xlbs and other 11xlbs
\(\\ \sf\longmapsto x+11x=132\)
\(\\ \sf\longmapsto 12x=132\)
\(\\ \sf\longmapsto x=\dfrac{132}{12}\)
\(\\ \sf\longmapsto x=11lbs\)
\(\\ \sf\longmapsto 11x=121lbs\)
Answer:
Step-by-step explanation:
.
Please help me the question

Answers
The polynomials completely factorized have the following expressions;
50). x³ - 3x² - 26x - 12 = (x - 6)(x + 1)(x + 2)
51). x³ - 12x² + 12x + 80 = (x - 10)(x + 2)(x - 4)
52). x³ - 18x² + 95x + 126 = (x - 9)(x - 2)(x - 7)
53). x³ - x² + 21x + 45 = (x + 5)(x - 3)(x - 3)
How to factorise the polynomials completelyFor the polynomial x³ - 3x² - 26x - 12 divisible by x - 6;
(x³ - 3x² - 26x - 12)/(x - 6) = x² + 3x + 2
x² + 3x + 2 = (x + 1)(x + 2)
so;
x³ - 3x² - 26x - 12 = (x - 6)(x + 1)(x + 2)
For the polynomial x³ - 12x² + 12x + 80 divisible by x - 10;
(x³ - 12x² + 12x + 80)/(x - 10) = x² - 2x - 8
x² - 2x - 8 = (x + 2)(x - 4)
so;
x³ - 12x² + 12x + 80 = (x - 10)(x + 2)(x - 4)
For the polynomial x³ - 18x² + 95x + 126 divisible by x - 9;
(x³ - 12x² + 12x + 80)/(x - 9) = x² - 9x + 14
x² - 9x + 14 = (x - 2)(x - 7)
so;
x³ - 18x² + 95x + 126 = (x - 9)(x - 2)(x - 7)
For the polynomial x³ - x² + 21x + 45 divisible by x + 5;
(x³ - x² + 21x + 45)/(x + 5) = x² - 6x + 9
x² - 6x + 9 = (x - 3)(x - 3)
so;
x³ - x² + 21x + 45 = (x + 5)(x - 3)(x - 3)
Therefore, by complete factorization the expressions (x - 6)(x + 1)(x + 2), (x - 10)(x + 2)(x - 4), (x - 9)(x - 2)(x - 7), and (x + 5)(x - 3)(x - 3) are the factors of their respective polynomial.
Read more about polynomial here:https://brainly.com/question/8021175
#SPJ1
Two cars start moving from the same point. One travels south at 50 mi/h and the other travels west at 20 mi/h. At what rate is the distance between the cars increasing 2 hours later? Round the result to the nearest hundredth.
Answers
The rate at which the distance between the cars is increasing 2 hours later is 0 mi/h, by using the Pythagorean theorem.
To find the rate at which the distance between the cars is increasing, we can use the Pythagorean theorem, which states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides.
Let's assume that after 2 hours, the distance traveled by the southbound car is d_south and the distance traveled by the westbound car is d_west.
Since the southbound car travels at a speed of 50 mi/h for 2 hours, we have d_south = 50 mi/h \(\times\) 2 h = 100 mi.
Similarly, the westbound car travels at a speed of 20 mi/h for 2 hours, so d_west = 20 mi/h \(\times\) 2 h = 40 mi.
Now, we can use the Pythagorean theorem to find the distance between the two cars:
\(distance^2 = d_south^2 + d_west^2distance^2 = 100^2 + 40^2distance^2 = 10000 + 1600distance^2 = 11600\)
distance ≈ sqrt(11600) ≈ 107.68 mi
To find the rate at which the distance between the cars is increasing, we differentiate the equation with respect to time:
2 \(\times\) distance \(\times\) \(\(\frac{{d(\text{{distance}})}}{{dt}}\)\) = 2 \(\times\) d_south \(\times\) \(\(\frac{{d(d_{\text{{south}}})}}{{dt}}\)\) + 2 \(\times\) d_west \(\times\) (d(d_west)/dt)
Since d_south and d_west are constant (no mention of their rates of change), we can simplify the equation to:
2 \(\times\) distance \(\times\) \(\(\frac{{d(\text{{distance}})}}{{dt}}\)\) = 0
Therefore, the rate at which the distance between the cars is increasing 2 hours later is 0 mi/h.
For more questions on Pythagorean theorem:
https://brainly.com/question/27997683
#SPJ8
Which point is represented by 6 times the quantity cosine 11 pi over 6 plus i times sine 11 pi over 6 end quantity question mark

Answers
\(6\left[\cos\left( \frac{11\pi }{6} \right) +i\sin\left( \frac{11\pi }{6} \right) \right] \\\\\\ 6\left[\cfrac{\sqrt{3}}{2}~~,~-\cfrac{1}{2}i \right]\implies (3\sqrt{3}~~,~-3i) ~~ \approx ~~ \stackrel{ \textit{\LARGE S} }{(5.2~~,~-3i)}\)
A large community college has professors and lecturers. The total number of faculty members is 228. The school reported that they have 5 professors every 14 lecturers How many of each type of faculty member does the community college employ?
Answers
There are 60 professors and 168 lecturers according to the given information.
What is arithmetic?
Arithmetic is an elementary a part of arithmetic that consists of the study of the properties of the normal operations on numbers—addition, subtraction, multiplication, division, involution, and extraction of roots.
Main BODY:
Let X be the number of professors and Y be the number of lecturers. As the total of both is 228:
X + Y = 228
Then, as there are 5 professors for every 14 lecturers:
5 X = 14 Y or X = (14/5) Y
Replacing this last value of X on the first equation:
(14/5) Y + Y = 228
(14/5) Y + (5/5) Y = 228
(19/5) Y = 228
Y = 228 * (5/19)
Y = (228*5)/19
Y = 1140 / 19
Y = 60
Then we can find X:
X = (14/5) Y = (14/5) * 60 = 168
X = 168
Hence thre are 60 professors and 168 lecturers.
To know more about arithmetic , visit:
brainly.com/question/24536701
#SPJ1
Pls help me I really don’t know

Answers
Answer:
1232 => 1
2464 => 2
6160 => 5
9856 => 8
Step-by-step explanation:
Each face of a pyramid is an isosceles with 80° vertex angle. what are the measures of base angles?The measures of the base angles are _°
Answers
The 3 interior angles in every triangle add up to 180 degrees, and in isosceles triangles the two base angles are the same, so:
180=80+2x
180-80=2x
100=2x
x=100/2=50 degrees
The measures of the base angles are 50 degrees
8. The table shows four transactions (in dollars) for a bank account. The balance
before the transactions was $89.50. What is the balance after the transactions?
Show your work
Date
Transaction Type
Deposit Withdrawal
17.25
11/4
11/4
11/7
35.90
10.77
11/11
3.02
Step by step pls

Answers
Our starting value: $89.50.
Deposits means putting money in the account, so money will increase.
Withdrawal means that you are depleting the account, so money will decrease.
1. 11/4 - Deposited $17.25
So you will add $89.50 + $17.25 = $106.75
2. 11/4 = Withdrawal $35.90
So you will subtract $106.75 - $35.90 = $70.85
3. 11/7 - Deposit $10.77
So you will add $10.77 + $70.85 = $81.62
4. 11/11 - Withdrawal of $3.02
So you will now subtract $81.62- $3.02 = $78.60
$78.60 is our final balance! I hope this helps!
Determine the perimeter of the composite figure.

Answers
Answer:84.7
Step-by-step explanation: you add up all the side lengths
area = 255 \(m^{2}\)
perimeter = 20+6.7+8+8+15+26 = 83.7m
Step-by-step explanation:
top left triangle - base is 3 because (20-8-9). so 1/2 bh = 1/2 (3) (6) = 9
left rectangle = l x w = 20 x 6 = 120
middle square = l x w = 8 x 9 = 72
lower right triangle = height is 12 because (26-8-6), so 1/2 bh =1/2 (9)(12) = 54
9+120+72+54 = 255
I need help with some math questions it may take a while tho

Answers
The intercept of a line is the y-coordinate of the point where the line crosses the y-axis, in this case, we can see from the graph that the line goes through the origin, then the intercept of the line b is 0
An ion channel can be in either open (O) or closed (C) states. If it is open, then it has probability 0.1 of closing in 1 microsecond; if closed, it has probability 0.3 of opening in 1 microsecond. Calculate the probability of the ion channel going through the following sequence of states: COO. An individual can be either susceptible (S) or infected (I), the probability of infection for a susceptible person is 0.05 per day, and the probability an infected person becoming susceptible is 0.12 per day. Calculate the probability of a person going through the following string of states: SISI.
Answers
Answer:
a) P (COO) = 0,135
b) P ( SISI) = 0,00015
Step-by-step explanation:
a) the probability of an ion channel in open position is 50 % 0,5
the probability of an ion channel in close position is 50 % 0,5
probability for the following sequence of states COO
to be closed 0,5 (C)
from (C) to pass to open 0,3 (O)
and to stay O is 0,9
Then the probability of the sequence of states COO is
P (COO) = 0,5 * 0,3 * 0,9
P (COO) = 0,135
b) If people are either infected or susceptible, then
Probability of an individual infected is 0,5
Probability of an individual susceptible is 0,5
to pass from susceptible to infected is 0,05
to pass from infected to susceptible is 0,12
then
P ( SISI) = 0,5 * 0,05*0,12*0,05
P ( SISI) = 0,00015
probability for the following sequence of states COO
Use the Law of Sines to solve (if possible) the triangle. If two solutions exist, find both. Round your answers to two decimal places. (If not possible, enter IMPOSSIBLE.) A = 72°, a = 34, b = 21
Answers
Answer:
Given: A = 72°, a = 34, b = 21
Calculated: B = 35.97°, C = 72.03°, c = 34.00
Step-by-step explanation:
\( \dfrac{\sin A}{a} = \dfrac{\sin B}{b} \)
\( \dfrac{\sin 72^\circ}{34} = \dfrac{\sin B}{21} \)
\( \sin B = \dfrac{21\sin 72^\circ}{34} \)
\( \sin B = 0.5874 \)
\( B = \sin^{-1} 0.5874 \)
\( B = 35.97^\circ \)
C = 180° - 72° - 35.97°
C = 72.03°
\( \dfrac{\sin A}{a} = \dfrac{\sin C}{c} \)
\( \dfrac{\sin 72^\circ}{34} = \dfrac{\sin 72.03^\circ}{c} \)
\(c = \dfrac{\sin 72.03^\circ \times 34}{\sin 72^\circ}\)
\( c = 34.00 \)
Given: A = 72°, a = 34, b = 21
Calculated: B = 35.97°, C = 72.03°, c = 34.00
Answer:
\(B\approx35.97^\circ\\C\approx72.03^\circ\\c\approx34\)
Step-by-step explanation:
Law of Sines
\(\frac{sinA}{a}=\frac{sinB}{b}=\frac{sinC}{c}\)
Given information
\(A=72^\circ\\a=34\\b=21\)
Check if solutions exist
As \(A=72^\circ < 90^\circ\) and that \(a > b\rightarrow 34 > 21\), then there exists only one possible triangle by the Ambiguous Case
Solve the triangle
\(\frac{sin(72^\circ)}{34}=\frac{sin(B)}{21}\\ \\ 21sin(72^\circ)=34sin(B)\\\\\frac{21sin(72^\circ)}{34}=sin(B)\\ \\B=sin^{-1}(\frac{21sin(72^\circ)}{34})\\ \\B=35.97394255^\circ\approx35.97^\circ\)
\(A+B+C=180^\circ\\\\72^\circ+35.97394255^\circ+C=180^\circ\\\\107.97394255^\circ+C=180^\circ\\\\C=72.02605745^\circ\approx72.03^\circ\)
\(\frac{sin(72^\circ)}{34}=\frac{sin(72.02605745^\circ)}{c}\\\\c*sin(72^\circ)=34sin(72.02605745^\circ)\\\\c=\frac{34sin(72.02605745^\circ)}{sin(72^\circ)}\\ \\c=34.00502065\approx34\)
Ringani worked overtime to raise a total amount R30 000.00 to settle his student debt. If he has deposited R8 500.00 yearly into an account earning 7,04% interest per year compounded annually. How long, rounded to one decimal place did it took her to accumulate the total amount? A. 3.0 years B. 2.4 years C. 2.8 years D. 2.0 years
Answers
It took Ringani 2.8 years to accumulate the total amount of R30,000.00 by depositing R8,500.00 yearly into the account with a 7.04% interest rate Compounded annually.The correct answer choice is C. 2.8 years.
To determine how long it took Ringani to accumulate the total amount of R30,000.00 by depositing R8,500.00 yearly into an account with a 7.04% interest rate compounded annually, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A is the final amount
P is the principal amount (initial deposit)
r is the interest rate (in decimal form)
n is the number of times the interest is compounded per year
t is the time in years
In this case, we have:
P = R8,500.00
A = R30,000.00
r = 7.04% = 0.0704 (in decimal form)
n = 1 (compounded annually)
We want to find the value of t.
Using the formula, we can rearrange it to solve for t:
t = (log(A/P)) / (n * log(1 + r/n))
Substituting the given values, we have:
t = (log(30,000/8,500)) / (1 * log(1 + 0.0704/1))
Calculating this using a calculator, we find that t is approximately 2.8 years.
Therefore, it took Ringani approximately 2.8 years (rounded to one decimal place) to accumulate the total amount of R30,000.00 by depositing R8,500.00 yearly into the account with a 7.04% interest rate compounded annually.
The correct answer choice is C. 2.8 years.
For more questions on Compounded .
https://brainly.com/question/31474686
#SPJ8
Enter a formula using k to connect the two variables. t is proportional to x .
Answers
Answer:
x:y I think this answer is correct
Step-by-step explanation:
Two functions are defined as follows.
•f(x) = x2 – 2x – 1
•g(x) = 2x - 1
Determine a simplified expression to represent (f.g)(x). Use the on-screen keyboard to type the correct answer in the box.
(f•g)(x)=
PLEASE HELP, I HAVE LIMITED TIME!

Answers
The value of f(g(x)) is 4x² – 8x+ 2 .
What is function?An expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
Given:
f(x) = x² – 2x – 1
g(x) = 2x - 1
So, f(g(x))
=f(2x - 1)
=(2x-1)² – 2(2x-1) – 1
=4x² – 4x + 1 -4x + 2 -1
=4x² – 8x+ 2
hence, the value of f.g(x) is 4x² – 8x+ 2 .
Learn more about function here:
https://brainly.com/question/22056199
#SPJ5
2
5
9
10
Which statements are true? Select the two correct answers.
The square root of a positive number greater than 1 is less than the number.
The square root of a positive number is always less than half of the number itself.
The square root of a positive number less than 1 is less than the number.
The square root of a perfect square is not a whole number.
The square root of a positive number less than 1 is between 0 and 1.
TIME REM
38:-
Answers
Answer:
The square root of a positive number greater than 1 is less than the number The square root of a positive number is less than half of the number itselfSelect the correct answer. log(2x-100) = 3
What is the solution to this equation?

Answers
Answer:
550
Step-by-step explanation:
Rewrite in exponential form:
10^3=2x-100
Solve for x:
1000= 2x-100
2x=1100
x=550
The solution to this equation is x =550
What is logarithm?In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a given number x is the exponent to which another fixed number, the base b, must be raised, to produce that number x.
Given
Rewrite in exponential form:
10³=2x-100
Solve for x:
1000= 2x-100
2x=1100
x=550
To know more about logarithm refer to :
https://brainly.com/question/12049968
#SPJ2
Candace sold 125 stickers on Monday. This is 50% of the total amount she sold during the whole week. How many stickers did she sell in all?
25 stickers
75 stickers
250 stickers
350 stickers
Answers
Answer: I THINK 250
Step-by-step explanation: 125 is half and 125 times 2 is 250.
What is the solution to this question im putting all my points on it. 3(a- 4) + 1 =9-a
Answers
why:
first you simplify both sides of the equation.
then you distribute and combine like terms
then you add a to both sides
and then add 11 to both sides
then divide both sides by four
a=5
Two separate samples receive two different treatments. The first sample has n = 9 with SS = 710, and the second has n = 6 with SS = 460. Compute the pooled variance for the two samples.
Answers
Answer:
The pooled variance for the two samples is 90
Step-by-step explanation:
Here in this question, we are interested in computing the pooled variance for the two given samples.
From the question;
n1 = 9
ss1 = 710
n2 = 6
ss2 = 460
The pooled variance can be calculated using a mathematical formula as shown below;
S^2 =( ss1 + ss2)/(n1 + n2 -2)
where S^2 refers to the pooled variance of both samples.
Plugging the values into the equation, we have ;
S^2 = (710 + 460)/9 + 6 -2 = 1170/13 = 90
Solve. Write the solution in interval notation.

Answers
The solution in interval notation is; (-∞, 49/2).
What is inequality?Inequality is defined as the relation which makes a non-equal comparison between two given functions.
To solve the equation 5/16x - 7/4 < 3/4x + 21/2, we can simplify both sides:
5/16x - 7/4 < 3/4x + 21/2
Combining like terms:
5/16x -3/4x < 21/2 + 7/4
8/16x < 49/4
1/2x < 49/4
Simplifying the fraction;
x < 49/2
Therefore, the solution in interval notation is (-∞, 49/2).
Learn more about Inequality here:
brainly.com/question/20383699
#SPJ1
Select the correct answer from each drop-down menu. A graph of quadrilateral 1 with the nodes of (minus 3, 7), (minus 4, 9), (minus 7, 9), and (minus 4, 5). Transformation of quadrilateral 2 with the nodes of (3, minus 4), (3, 6), (8, 2.8), and (7.2, minus 1.9). Quadrilateral 1 and quadrilateral 2 are polygons that can be mapped onto each other using similarity transformations. The transformation that maps quadrilateral 1 onto quadrilateral 2 is a followed by a dilation with a scale factor of .
Answers
This transformation of the polygon ABCD to A'B'C'D' is a by a factor of 2√5.
The coordinates are given as:
First polygon: A (-3, 7), B (-4, 9), C (-7, 9), and D (-4, 5).
Second polygon: A' (3, -4), B'(3, 6), C'(8, 2.8), and D'(7.2, -1.9)
Calculate the distance AB and A'B' using:
⇒ d = √ (x₂ - x₁)² + (y₂ - y₁)²
⇒ AB = √ (-4 + 3)² + (9 - 7)²
⇒ AB = √1 + 4
⇒ AB = √5
⇒ d = √ (x₂ - x₁)² + (y₂ - y₁)²
⇒ A'B' = √ (3 - 3)² + (6 + 4)²
⇒ A'B' = 10
This gives, Divide A'B' by AB to determine the scale factor (k)
k = 10 / √5
k = 2√5
Hence, this transformation is a by a factor of 2√5
Read more about transformation at:
brainly.com/question/4289712
#SPJ1
Answer:
Reflection and 2
Step-by-step explanation:
for plato