If a1 =7 and a n =4a n−1 then find the value of a 4 .
Answers
The value of a₄ is 19.
What is arithmetic progression?
A progression or sequence of numbers known as an arithmetic sequence maintains a consistent difference between each succeeding term and its predecessor. The common difference in that mathematical progression is the constant difference.
Here, we have
Given: a₁ =7 and aₙ = aₙ₋₁ + 4
We have to find the value of a₄.
a₁ =7
aₙ = aₙ₋₁ + 4
aₙ - aₙ₋₁ = 4
The common difference is 4.
In order to solve, replace the value of the previous answer with the equation for the next answer.
a₁ = 7
a₂ = 7 + 4 = 11
a₃ = 11 + 4 = 15
a₄ = 15 + 4 = 19
Hence, the value of a₄ is 19.
To learn more about the arithmetic progression from the given link
https://brainly.com/question/6561461
#SPJ1
Related Questions
Please help! I will mark brainliest:)
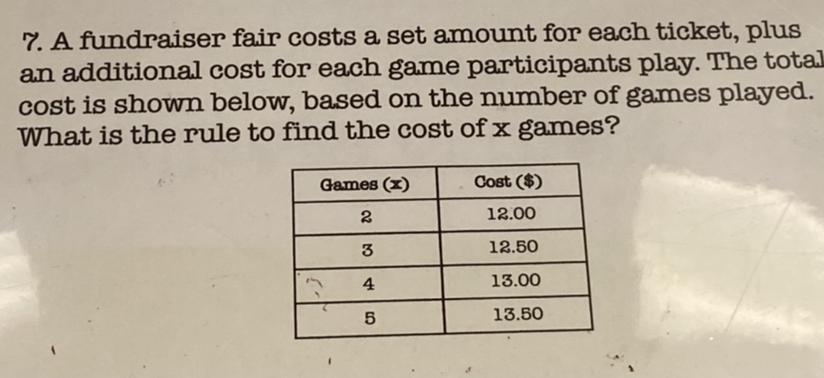
Answers
Answer: y = 12.00 + (0.50)*(x - 2)
Step-by-step explanation:
x will be the game
y = cost
x - 2 because 2 is the initial
you can test it y = 12 + (0.50)*(3-2)
y = 12 +(0.50)*(1)
y = 12.50
How much interest is earned on a $5,000 loan at 10% interest for 3 years?
$15,000
$125
$1,500
$150,000
Answers
Answer:
$1500
.................
Answer:
$1,500
Step-by-step explanation:
What is the value of the expression below when y=7?
y2+5y+6
Answers
Answer:
90
Step-by-step explanation:
y^2 + 5y + 6 =
(7)^2 + 5(7) + 6 =
49 + 35 + 6 =
84 + 6 =
90
7^2 + 5(7) + 6
49 + 35 + 6
90
i dont know help me i am so confused?

Answers
Answer:
the answer should be 16, if you're looking for X that is
Write your question here (Keep it simple and clear to get the best answer)When A Number Is Subtracted From 1010001 the Difference Is 910002 find The Number?
Answers
Answer:
\(99999\)
Step-by-step explanation:
Let the number be \(x\).
According to question, if a number is subtracted from 1010001 the difference is 910002.
\(1010001-x=910002\)
Transpose \(1010001\) to the right side of the equation.
\(-x=910002-1010001=-99999\\-x=-99999\)
Multiply both sides by \(-1\)
\(-x(-1)=-99999(-1)\\x=99999\)
So, if \(99999\) is subtracted from 1010001 the difference is 910002.
Use the marginal tax rate chart to answer the question. Tax Bracket Marginal Tax Rate $0–$10,275 10% $10,276–$41,175 12% $41,176–$89,075 22% $89,076–$170,050 24% $170,051–$215,950 32% $215,951–$539,900 35% > $539,901 37% Determine the effective tax rate for a taxable income of $180,900. Round the final answer to the nearest hundredth.
19.50%
20.00%
21.11%
32.00%
Answers
For a taxable income of $1,80,900, the effective tax rate is 21.11%.
what is meant by marginal tax?Marginal tax is the tax rate applied to an individual’s last dollar of income. It is the additional tax that must be paid on any additional income earned. In other words, it is the tax rate that applies to an individual’s income after all deductions. For example, if an individual’s income is $50,000 and the marginal tax rate is 25%, then the individual must pay an additional $12,500 in taxes on top of the $25,000 in taxes already paid on their $50,000 income.
Marginal tax rates are progressive, meaning that as an individual’s income increases, the marginal tax rate will increase as well. The marginal tax rate is important to understand because it helps individuals determine how much additional income they will need to earn in order to make up for the taxes they will have to pay on that income. It is also important to understand how marginal tax rates can affect tax planning strategies.
To determine the effective tax rate for a taxable income of $180,900, calculate the sum of the marginal tax rates for each tax bracket that the $180,900 falls into. The taxable income of $180,900 is greater than $89,075 and less than $170,050. The marginal tax rates for these two tax brackets are 22% and 24%, respectively. The sum of the marginal tax rates is 46%. Divide the sum by the taxable income of $180,900 to get the effective tax rate of 21.11%. Round the final answer to the nearest hundredth to get 21.11%.
To learn more about marginal tax refer to:
https://brainly.com/question/29029623
#SPJ1
Help me please I don't know how to solve this problem.

Answers
In, functions F and G are defined by formulas. Find G ◦ F and F ◦ G and determine whether G ◦ F equals F ◦ G.
Exercise
F(x)= x5 and G(x)= x1/5 for all real numbers x.
Answers
To evaluate the given integral, we will use partial fractions decomposition. This involves breaking down the fraction into simpler fractions with denominators that can be easily integrated.
Let's start by decomposing the given fraction, 1/(x(x−2)²), using partial fractions. We need to express it as a sum of fractions with simpler denominators.
First, we factor the denominator: x(x−2)². The factors are x, (x−2), and (x−2) again. Therefore, we can write the partial fraction decomposition as:
\(\frac{1}{(x(x-2)^2)}= A/x + B/(x-2) + C/(x-2)^2\)
To find the constants A, B, and C, we can use the method of equating coefficients. We multiply both sides of the equation by the denominator to clear the fractions:
\(1 = A(x-2)^2 + Bx(x-2) + Cx\)
Next, we can substitute some convenient values of x to solve for the constants. Choosing x=0, x=2, and x=3 will give us three equations, allowing us to determine the values of A, B, and C.
Once we find the constants, we integrate each term individually. The integral of 1/x is ln|x|, the integral of 1/(x−2) is ln|x−2|, and the integral of \(\frac{1}{((x-2)^2)}\) is −1/(x−2).
Finally, we sum up the integrals of each term, and include the arbitrary constant C to account for all possible solutions.
Therefore, the evaluated integral is:
∫\(\frac{1}{(x(x-2)^2)}\) dx = A ln|x| + B ln|x−2| − C/(x−2) + C + C
Here, the constants A, B, and C are determined by solving the equations obtained from the partial fractions decomposition process.
Learn more about denominator here: https://brainly.com/question/15007690
#SPJ11
Based on the following new information. Given it is raining, what is the what is the probability of Sunshine delight winning ?
Storm Chaser Sunshine delight
Given Raining 0.79 Given not raining 0.64
Based on the following information collected from emails. What is the probability that if the word "llwws" is in a document, it is spam ?
Spam Not spam
Word "aabbdd" 0.71 Word "llwws" 0.5
ROUND TO 2 DECIMAL PLACES
Answers
The probability of Sunshine Delight winning given that it is raining is approximately 0.79. The probability that a document is spam if it contains the word "llwws" is approximately 0.50.
In the case of Sunshine Delight winning, given that it is raining, the probability is directly provided as 0.79.
For the probability of a document being spam if it contains the word "llwws," the information shows that the probability of the word "llwws" appearing in a spam document is 0.50. However, without further information about the overall prevalence of spam and non-spam documents, we cannot directly determine the probability that a document containing "llwws" is spam. Additional context about the overall occurrence of spam and non-spam documents is required to calculate the requested probability.
Learn more about probability here: brainly.com/question/13604758
#SPJ11
Complete the square to re-write the quadratic function in vertex form:

Answers
Answer:
(x+2)^2 - 6
Step-by-step explanation:
1-0.004326suppose it is believed that the probability a patient will recover from a disease following medication is 0.8. in a group of ten such patients, the number who recover would have mean and variance respectively given by (to one decimal place):
Answers
The mean number of patients who recover is 8, and the variance is 1.6.
This scenario follows a binomial distribution, where the number of patients who recover from the disease out of a sample of ten patients follows a binomial distribution with parameters n = 10 (sample size) and p = 0.8 (probability of success).
The mean (μ) and variance (σ^2) of a binomial distribution are given by
μ = np
Substitute the values in the equation
= 10 x 0.8
Multiply the numbers
= 8
σ^2 = np(1-p)
Substitute the values in the equation
= 10 x 0.8 x (1-0.8)
= 1.6
Learn more about binomial distribution here
brainly.com/question/29156955
#SPJ4
-
Solve the system of equations – 2z – 2y = -24 and 3z – 2y = -33 by
combining the equations.
-
( 2z -2y =-24)
– 32 -2y =-33)
-
-
-22 -2y = -24
-32 -2y -33
0 - 0 Y=
You must answer all questions above in order to submit.
P
Answers
Answer:
z = -1.8, y = 10.2
Step-by-step explanation:
- 2z -2y = -24 (EQ 1)
3z - 2y = -33 (EQ 2)
Change one of the equations to it's opposite (Turning a negative number to a positive/or the other way around)
Let's target the equation that can leave us with the simplest question to solve
-2z + -2y = -24
-3z + 2y = 33
-5z = 9
(Dividing and switching the negative sign over)
z = -1.8
Plug in Z to solve for y.
-2(-1.8) - 2y = -24
3.6 - 2y = -24
-2y = -20.4
y = 10.4
Find the equation of the line shown.
please I need it soon as possible

Answers
Answer:
Y=2x+0.5
Step-by-step explanation:
The gradient is 2/1=2x
The y-intercept looks to be around 0.5
Answer:
y = \(\frac{1}{2}\) x + \(\frac{1}{2}\)
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
Calculate m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 1, 0) and (x₂, y₂ ) = (1, 1) ← 2 points on the line
m = \(\frac{1-0}{1-(-1)}\) = \(\frac{1}{1+1}\) = \(\frac{1}{2}\) , then
y = \(\frac{1}{2}\) x + c ← is the partial equation
To find c substitute either of the 2 points into the partial equation
Using (1, 1 ) , then
1 = \(\frac{1}{2}\) + c ⇒ c = 1 - \(\frac{1}{2}\) = \(\frac{1}{2}\)
y = \(\frac{1}{2}\) x + \(\frac{1}{2}\) ← equation of line
When solving for x, the sine of 33º is used. What other angle and trigonometric function could be used to solve for x? a. cos 57º c. tan 57º b. tan 33º d. cos 33º
hurry
Answers
Answer:
The answer is A.Cos 57.
Step-by-step explanation:
Took the test..
For the standard normal distribution, which below statement is correct? A. Standard Deviation is 1 . Variance is 1 and Mean is 1 . B. Standard Deviation is 0 . Variance is 1 and Mean is 1 . C. Standard Deviation is 1 . Variance is 0 and Mean is 0 . D. Standard Deviation is 1 . Variance is 1 and Mean is 0 .
Answers
The statement that is correct for the standard normal distribution is D. Standard Deviation is 1. Variance is 1 and Mean is 0. The standard normal distribution is a normal distribution that has a mean of 0 and a standard deviation of 1.
The standard normal distribution, often known as the Z distribution, is a normal distribution in which the mean is 0 and the variance is 1. A normal distribution has two parameters: the mean and the variance, denoted by μ and σ², respectively.
However, for the standard normal distribution, these values are standardized to 0 and 1, respectively. The standardized values of a normal distribution are referred to as Z-scores or standardized values. For any normal distribution with mean μ and standard deviation σ, the formula for the standardized value Z is Z = (X - μ)/σ.
The standard normal distribution has several critical characteristics, including the fact that it is symmetrical, bell-shaped, and unimodal.
Furthermore, the area under the standard normal curve is equal to 1, and the curve is asymptotic to both axes. Additionally, the Z distribution is beneficial since it makes it easy to compare data sets that are based on different scales or units by converting each data point into a standard unit of measure.
The statement that is correct for the standard normal distribution is D. Standard Deviation is 1. Variance is 1 and Mean is 0.
To know more about standard deviation :
brainly.com/question/29115611
#SPJ11
3/2x+1 = 13
find x.
What is x?
Answers
you subtract 1 on both sides and u get 3/2x=12 and when you dive 3/2 on both sides you get 1/8
Answer:
8
Step-by-step explanation:
Please write this as (3/2)x + 1 = 13.
Start the process of solving for x by subtracting 1 from both sides:
(3/2)x = 12
Eliminate the fractional coefficient by multiplying both sides by 2/3:
(2/3)(3/2)x = (2/3)(12), or
x = 8
what is the smallest positive integer $n$ such that $\frac{1}{n}$ is a terminating decimal and $n$ contains the digit $9$?
Answers
The smallest positive integer n, such that 1 / 9 is a terminating decimal and n contains 9 is 4, 096.
How to find the smallest positive integer ?Finite digits terminating after the decimal point represent what are known as "terminating decimals". This type of decimal is characterized by their limited representation which comes to an end after a specific number of digits.
The smallest positive integer to satisfy the conditions, of the terminating decimals would be in the form 2 ^ r 5 ^ s.
We can then solve for the smallest positive integer n, to be:
= 2 ¹² x 5 ⁰
= 4 ,096
Find out more on smallest positive integers at https://brainly.com/question/28145478
#SPJ1
You spend $23 to spend on 4 avocados. After buying them you had $11. How much did each avocado cost? Write an equation about this.
Answers
Answer: Each avocado cost $3
Equation: 23 - 4x = 11
Answer:
$3 per avocados
Step-by-step explanation:
23-11= 12. 12 divided by 4 = 3
The function h (x) = startfraction 2 (x 3) over x endfraction is a result of the composition (g ∘ f)(x). if g (x) = startfraction 2 over x endfraction, what is f(x)? f (x) = startfraction 1 over x 3 endfraction f (x) = startfraction x over x 3 endfraction f(x) = x 3 f (x) = startfraction x 3 over x endfraction
Answers
The value of the function f(x) = 2x/(2x + 3).
What is defined as the function?A function is defined as a relationship between a set of inputs that each have one output.
A function is a connection between inputs in which each input is related to precisely one output. Every function does have a domain and a co-domain, as well as a range. In general, a function is denoted by f(x), where x is the input.Now, as per the question, the functions are give as;
h(x) = (2x + 3)/x
g(x) = 2/x
And, g(f (x) ) = h(x) = (2x + 3)/x ......(equation 1)
To estimate the value of f (x); Substitute x for f(x)
g(f (x) ) = 2/f (x) ......(equation 2)
Equation (equation 1 and 2).
2/f (x) = (2x + 3)/x
f (x) = 2x/ (2x + 3)
Thus, the value of the function f (x) = 2x/ (2x + 3).
To know more about the function, here
https://brainly.com/question/25638609
#SPJ4
The correct question is-
The function h (x) = StartFraction 2 (x + 3) Over x EndFraction is a result of the composition (g compose f) (x). If g (x) = StartFraction 2 over x EndFraction, what is f(x)?
When we are computing a simple linear regression line, there are certain conditions that must be met for this model to be valid. One of these conditions is the equal spread condition. Which of these answers best explains how we check to make sure that this condition is met? a. Make sure there is similar spread around the sample mean of x. b. Make sure there is similar spread around the line at each value of x.
c. Make sure that there is similar spread around the sample mean of y. d. Make sure all outliers are only below the line.
Answers
The answers that best explains how we check to make sure that this condition is met is: c. Make sure there is similar spread around the sample mean of y.
How we check to make sure that this condition is met?The equal spread condition states that the residuals (differences between the actual and predicted values of y) should have roughly equal variance at each value of x.
To check if this condition is met, we examine the residual plot, which is a scatterplot of the residuals versus the independent variable x. If the spread of residuals around the mean is roughly equal for all x, then the equal spread condition is satisfied.
Therefore the correct option is C.
Learn more about actual and predicted values here:https://brainly.com/question/28610444
#SPJ1
1
-6a × -
2
Another time :/ , I'm studying for my post mid term exams..
Answers
Answer:
a×
a×_
a×_12
Step-by-step explanation:
1
_
-6
_
2
6×2=12
a×
_
6
_
2
ax
_12
Factored Form:5r + 4r^4I NEED ALL THE EQUATION PLEASE
Answers
to factor we must recognize the elements in common
the r exist on both terms, so we can divide by r on each term to factor
\(undefined\)Joan is 5 years older than Ellen, and 3 years ago their sum of their ages is 17, in how many years will Joan be 21?
Answers
Answer:
7
Step-by-step explanation:
Sarah and her 3 friends split a bag of candy evenly. They each ate 13 pieces of candy and there were 2 pieces leftover. How many pieces of candy were originally in the bag
Answers
4 people in all, each ate 13. 4*13=52. 2 were leftover, so 52+2=54
The graphs of the functions f and g are shown in the figure.
The x y coordinate plane is given. There are 2 functions on the graph.
The function labeled f consists of 3 line segments. Function f begins at the point (−2, 0.5), goes linearly down and right to the origin where it sharply changes direction, goes linearly up and right, passes through the point (1, 2), sharply changes direction at the point (2, 4), goes linearly down and right, passes through the point (5, 3), and ends approximately at the point (7, 2.3).
The function labeled g consists of 2 line segments. Function g begins at the point (−2, 4), goes linearly down and right, passes through the point (-1, 3), crosses the y-axis at y = 2, passes through the point (1, 1), sharply changes direction at the point (2,0), goes linearly up and right, passes through the point (5, 2), and ends approximately at the point (7, 3.2).
Let u(x) = f(x)g(x) and
v(x) =
f(x)
g(x)
.
Answers
The output of each function include the following:
u'(1) = 0.
v'(5) = -2/3
How to determine the output of each function?By critically observing the graph of the functions f and g, we can logically deduce the following parameters;
f(1) = 2 f(5) = 3
g(1) = 1 g(5) = 2
f'(1) = 2 f'(5) = -1/3
g'(1) = -1 g'(5) = 2/3
Next, we would take the first derivative of u with respect to x and then, substitute the x-value into the composite function, and then evaluate as follows;
u(x) = f(x)g(x)
u'(x) = f'(x)g(x) + g'(x)f(x)
u'(1) = f'(1)g(1) + g'(1)f(1)
u'(1) = 2(1) + (-1)2
u'(1) = 2 - 2
u'(1) = 0.
For v'(5), we have the following function by applying quotient rule:
\(v'(x) = \frac{f'(x)g(x)\;-\;f(x)g'(x)}{g^2(x)} \\\\v'(5) = \frac{f'(5)g(5)\;-\;f(5)g'(5)}{g^2(5)} \\\\v'(5) = \frac{\frac{-1}{3} \times 2 - (3 \times \frac{2}{3}) }{2^2}\)
v'(5) = -8/3 × 1/4
v'(5) = -2/3
Read more on function here: https://brainly.com/question/31048166
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

Part B The physician prescribed Aldactone 20mg,PO,q12 h, for a 22-lb kid. The safe dosage range is 1 to 3.3mg/kg/24hr. a) Calculate the minimum and maximum dosage range for per dose. [4 marks] b) Is this a safe dose? Why? [2 marks] Part C Given that (x−1)(x−2)
5x+7
= x−1
A
+ x−2
B
where A and B are constants. Find the values of A and B. [4 marks] Part D a) Express 3cosθ−4sinθ in the form rcos(θ+α), where r>0 and 0 ∘
<α<90 ∘
[4 marks] b) Hence, find the maximum values of the function, stating the values of θ, between 0 ∘
and 360 ∘
, where the maximum value occurs. [3 marks]
Answers
the minimum dosage range per dose is approximately 0.499 mg and the maximum dosage range per dose is approximately 16.48 mg.
a) Given: Weight of the kid = 22 lb
To convert lb to kg, we use the conversion factor: 1 lb = 0.453592 kg
Weight in kg = 22 lb * 0.453592 kg/lb ≈ 9.98 kg
Minimum dosage per dose = 1 mg/kg/24hr * 9.98 kg / 2 doses = 0.499 mg
Maximum dosage per dose = 3.3 mg/kg/24hr * 9.98 kg / 2 doses ≈ 16.48 mg
Therefore, the minimum dosage range per dose is approximately 0.499 mg and the maximum dosage range per dose is approximately 16.48 mg.
b) Since the prescribed dose of 10 mg falls within the safe dosage range of 1 to 3.3 mg/kg/24hr, we can conclude that it is a safe dose.
To determine if the prescribed dose is safe, we compare it with the safe dosage range provided.
Given: Prescribed dose = 20 mg
The prescribed dose falls within the safe dosage range of 1 to 3.3 mg/kg/24hr. Since the prescribed dose is 20 mg and the weight of the kid is approximately 9.98 kg, the prescribed dose per 24 hours would be 20 mg / 2 doses = 10 mg.
Since the prescribed dose of 10 mg falls within the safe dosage range of 1 to 3.3 mg/kg/24hr, we can conclude that it is a safe dose.
Part C:
Therefore, the values of A and B are A = 2 and B = -1.
Given that (x - 1)(x - 2)/(5x + 7) = (x - 1)/A + (x - 2)/B
To find the values of A and B, we need to equate the numerators:
(x - 1)(x - 2) = (x - 1)B + (x - 2)A
Expanding the left side:
x^2 - 3x + 2 = (x - 1)B + (x - 2)A
Setting coefficients of like terms equal:
1 = B + A
-3 = -B - 2A
2 = -2B
From the first equation, we have B = 1 - A.
Substituting B in the third equation:
2 = -2(1 - A)
2 = -2 + 2A
4 = 2A
A = 2
Substituting A in the first equation:
1 = B + 2
B = -1
Therefore, the values of A and B are A = 2 and B = -1.
Part D:
a) 3cosθ - 4sinθ can be expressed in the form 5cos(θ + α), where r = 5 and α = tan^(-1)(4/3).
We have 3cosθ - 4sinθ. To express it in the form rcos(θ + α), we can use the identities:
cos(θ + α) = cosθ cosα - sinθ sinα
sin(θ + α) = sinθ cosα + cosθ sinα
Let's rewrite 3cosθ - 4sinθ as rcos(θ + α):
3cosθ - 4sinθ = rcos(θ + α)
Comparing the coefficients of cosθ and sinθ, we have:
3 = r cosα
-4 = r sinα
Dividing the equations, we get:
-4/3 = -tanα
Using inverse tangent (tan^(-1)), we find α:
α = tan^(-1)(4/3)
To find r, we can use the Pythagorean identity:
r^2 = (r cosα)^2 + (r sinα)^2
r^2 = (3^2) + (-4^2)
r^2 = 9 + 16
r^2 = 25
r = 5
Therefore, 3cosθ - 4sinθ can be expressed in the form 5cos(θ + α), where r = 5 and α = tan^(-1)(4/3).
b) the maximum values of the function occur at θ = -tan^(-1)(4/3) and θ = 180 - tan^(-1)(4/3) between 0 degrees and 360 degrees.
To find the maximum values of the function, we need to find the value of θ that maximizes the expression 3cosθ - 4sinθ.
The maximum value of 5cos(θ + α) occurs when θ + α = 0 or 180 degrees.
θ + α = 0
θ = -α
θ = -tan^(-1)(4/3)
θ + α = 180 degrees
θ = 180 - α
θ = 180 - tan^(-1)(4/3)
Therefore, the maximum values of the function occur at θ = -tan^(-1)(4/3) and θ = 180 - tan^(-1)(4/3) between 0 degrees and 360 degrees.
To know more about Pythagorean identity:
https://brainly.com/question/24220091
#SPJ11
using the results of part (a) find an orthonormal should be parallel to v0 and {w0,w1} should span the same subspace as {v0,v1}.
Answers
Given that v0 = (2, 1, -2), v1 = (-2, 1, 1), and v2 = (1, 2, 2), we can find the orthonormal basis that should be parallel to v0, and w0 and w1 should span the same subspace as v0 and v1.To find the orthonormal basis that should be parallel to v0.
we need to follow these steps:
Let v0 be a vector in Rn with nonzero norm ||v0||, and let V be the subspace of Rn that is perpendicular to v0 (so if y is in V, then y·v0 = 0).
Then, we can construct an orthonormal basis {v1, . . . , vp} for V, and {v0/v0, v1, . . . , vp} will be an orthonormal basis for Rn.
To find {v1, . . . , vp}, we apply Gram-Schmidt to the basis {v0, v1, . . . , vp}.
Specifically, we compute vi' = vi - projv0vi for i = 1, . . . , p.
This ensures that {v1, . . . , vp} are all in V and that {v0/v0, v1, . . . , vp} is an orthonormal basis for Rn that is parallel to v0.
So, in this case, we can take v0 = (2, 1, -2), which has norm ||v0|| = sqrt(2^2 + 1^2 + (-2)^2) = sqrt(9) = 3.
Now, we need to find w0 and w1 that span the same subspace as v0 and v1. Since {v0, v1} is a basis for this subspace, any two linearly independent vectors in this subspace will span the same subspace. So, we can just pick any two such vectors. Let w0 = (2, 1, -2) and w1 = (-2, 5, 1).
We claim that {w0, w1} is linearly independent and spans the same subspace as {v0, v1}.To show that {w0, w1} is linearly independent, suppose that aw0 + bw1 = 0 for some scalars a and b. Then, we have(2a - 2b, a + 5b, -2a + b) = (0, 0, 0).This gives us two equations:2a - 2b = 0a + 5b = 0
Solving for a and b, we geta = 5/7 and b = -2/7.
Since a and b are not both zero, this shows that {w0, w1} is linearly independent.
To show that {w0, w1} spans the same subspace as {v0, v1}, we need to show that every vector in this subspace can be written as a linear combination of w0 and w1. Let (x, y, z) be any vector in this subspace.
To know more about orthonormal visit:
https://brainly.com/question/33727806
#SPJ11
Divide and write answer in rectangular form
[2(cos25+isin25)]•[6(cos35+isin35]
Answers
The division of the given complex numbers in rectangular form is approximately 1/3 (cos10° - isin10°).
To divide the complex numbers [2(cos25° + isin25°)] and [6(cos35° + isin35°)], we can apply the division rule for complex numbers in polar form.
In polar form, a complex number can be represented as r(cosθ + isinθ), where r is the magnitude and θ is the argument (angle) of the complex number.
First, let's express the given complex numbers in polar form:
[2(cos25° + isin25°)] = 2(cos25° + isin25°)
[6(cos35° + isin35°)] = 6(cos35° + isin35°)
To divide these complex numbers, we can divide their magnitudes and subtract their arguments.
The magnitude of the result is obtained by dividing the magnitudes of the given complex numbers, and the argument of the result is obtained by subtracting the arguments.
Dividing the magnitudes, we have: 2/6 = 1/3.
Subtracting the arguments, we have: 25° - 35° = -10°.
Therefore, the division of the given complex numbers [2(cos25° + isin25°)] and [6(cos35° + isin35°)] can be written as 1/3 (cos(-10°) + isin(-10°)).
In rectangular form, we can convert this back to the rectangular form by using the trigonometric identities: cos(-θ) = cos(θ) and sin(-θ) = -sin(θ).
So, the division of the given complex numbers in rectangular form is approximately 1/3 (cos10° - isin10°).
To learn more about complex numbers click here: brainly.com/question/20566728
#SPJ11
"Complete question"
Divide And Write Answer In Rectangular Form[2(Cos25+Isin25)]•[6(Cos35+Isin35]
Her little sister's birthday is next week, so Erin is planning a bubble-themed birthday party!
She buys a big bottle of bubble solution and divides it equally among 8 small bottles. Each
small bottle holds
1
of a gallon of bubble solution.
16
Use an equation to find the amount of bubble solution in the big bottle.
To write a fraction, use a slash (/) to separate the numerator and denominator.
Answers
Answer:
The answer and solution is in the picture

An equation is formed of two equal expressions. The equation that can represent the amount of solution in a small bottle is x=y/8.
What is an equation?An equation is formed when two equal expressions are equated together with the help of an equal sign '='.
Let the bubble solution in the small bottle be represented by x, while the amount of solution in the big bottle is represented by y. Since the sum of the solution of 8 small bottles is equal to a big bottle. Therefore, the equation can be written as,
The amount of solution in the big bottle) = (Amount of solution in a small bottle)×8
y = 8x
x = y/8
Hence, the equation that can represent the amount of solution in a small bottle is x=y/8.
Learn more about Equation:
https://brainly.com/question/2263981
#SPJ2
a random sample of 150 u.s. adults is composed of 100 people from non-rural areas and 50 people from rural areas. estimate the confidence interval for the fraction of the population that is non-rural with 99% confidence. what is the lower limit of the confidence interval?
Answers
With 99% confidence, we can estimate that the fraction of the population that is non-rural is between 0.60 and 0.74.
To estimate the confidence interval for the fraction of the population that is non-rural with 99% confidence, we need to use the following formula:
Point estimate +/- (critical value * standard error)
Where the point estimate is the sample proportion of non-rural adults (100/150 = 0.67), the critical value is the z-score corresponding to a confidence level of 99% (2.575), and the standard error is the standard deviation of the sampling distribution of the sample proportion (which is equal to the square root of [(sample proportion * (1 - sample proportion)) / sample size]).
Plugging in the values, we get:
0.67 +/- (2.575 * sqrt[(0.67 * (1 - 0.67)) / 150])
Solving this equation gives us a lower limit of 0.60 for the confidence interval.
Thus, with 99% confidence, we can estimate that the fraction of the population that is non-rural is between 0.60 and 0.74.
To learn more about confidence interval, refer:-
https://brainly.com/question/24131141
#SPJ4