Answers
Answer:
The answer is option 2.
Step-by-step explanation:
Given that the TU and UF added up together to form a length of 32. In order to find TU, you have to subtract length of UF from 32 :
TU + UF = 32
TU + 20 = 32
TU = 32 - 20
TU = 12
Related Questions
A geologist gathered data about the total shoreline and maximum depth of several area lakes and organized the data into this table.
Total Shoreline (miles) 22 17 10 23 12 35 7
Maximum Depth (feet) 101 85 59 113 64 158 33
She then used a graphing tool to display the data in a scatter plot, with x representing the total miles of shoreline and y representing the maximum depth. She also used the graphing tool to find the equation of the line of best fit:
y = 4.26x + 10.908.
Based on the line of best fit, what is the approximate maximum depth of a lake that has 31 miles of shoreline?
Answers
Based on the line of best fit, the approximate maximum depth of a lake that has 31 miles of shoreline is; 142.968 ft
How to interpret a Line of best fit?The line of best fit is defined as a straight line which is drawn to pass through a set of plotted data points to give the best and most approximate relationship that exists between such data points.
Now, we are given a table of values that shows the total shoreline in miles which will be represented on the x-axis and then the maximum depth of several area lakes which will be represented on the y-axis.
However, when the geologist found the graph, she arrived at an equation of best fit as;
y = 4.26x + 10.908.
Thus, for 31 miles of shoreline, the approximate maximum depth is;
Approximate maximum depth = 4.26(31) + 10.908.
Approximate maximum depth = 142.968 ft
Read more about Line of best fit at; https://brainly.com/question/1441182
#SPJ1
Answer:
143 feet
Step-by-step explanation:
its technically 142 and change but edmentum rounds up
Cuál es el volumen de un cilindro que tiene 42cm de radio y una altura de 1.20m?
Answers
Answer:
V = 665,012 cm^2 (centímetros cuadrados)
Step-by-step explanation:
V= (pi) x (r^2) x (h)
V = 3.14 x 1764 x 120cm = 665012 cm^2
Marian Plunket owns her own business and is considering an investment. if she undertakes the investment, it will pay $28,000 at the end of each of the new 3 years. the opportunity requires an initial investment of $7,000 plus an additional investment at the end of the second year of $35,000. what is the NPV of this opportunity if the interest rate is 8% per year? Should Marian take it?
Answers
The NPV is positive, it is worth taking the Investment.
Net Present Value (NPV) is an assessment method that determines the attractiveness of an investment. It is a technique that determines whether an investment has a positive or negative present value.
This method involves determining the future cash inflows and outflows and adjusting them to their present value. This helps determine the profitability of the investment, taking into account the time value of money and inflation.The formula for calculating NPV is:
NPV = Σ [CFt / (1 + r)t] – CIWhere CFt = the expected cash flow in period t, r = the discount rate, and CI = the initial investment.
The given problem can be solved by using the following steps:
Calculate the present value (PV) of the expected cash inflows:
Year 1: $28,000 / (1 + 0.08)¹ = $25,925.93Year 2: $28,000 / (1 + 0.08)² = $24,009.11Year 3: $28,000 / (1 + 0.08)³ = $22,173.78Total PV = $72,108.82
Calculate the PV of the initial investment: CI = $7,000 / (1 + 0.08)¹ + $35,000 / (1 + 0.08)²CI = $37,287.43Calculate the NPV by subtracting the initial investment from the total PV: NPV = $72,108.82 – $37,287.43 = $34,821.39
Since the NPV is positive, it is worth taking the investment.
For more questions on Investment.
https://brainly.com/question/29227456
#SPJ8
A simple random sample of 25 items from a normally distributed population resulted in a sample mean of 28 and a standard deviation of 7.5. Construct a 95% confidence interval for the population mean.
Answers
Answer:
CI = 28 ± 3.09
Step-by-step explanation:
The sample size, n = 25
The sample mean, m = 28
Standard deviation, s = 7.5
Confidence interval is given as:
CI = Sample mean ± margin of error
We want to find 95% confidence level:
First, let us find the margin of error:
Margin of error = Critical value * standard error
To find the critical value, we need some parameters:
Standard error = \(s / \sqrt{n}\)
=> \(SE = 7.5 / \sqrt{25}= 7.5 = 5 = 1.5\)
The alpha value, ∝ = 1 - (confidence level / 100) = 1 - 95/100 = 1 - 0.95 = 0.05
Critical probability, p, is given as:
p = 1 - ∝/2 = 1 - 0.05/2 = 1 - 0.025 = 0.975
Now we need the degree of freedom:
df = n - 1 = 25 - 1 = 24
Therefore, the critical value is 2.06 (you can use an online t value calculator).
=> Margin of error = 2.06 * 1.5 = 3.09
Therefore, the confidence interval for the population mean is:
CI = 28 ± 3.09
Assuming everything else stays the same, an increase in the price of smartphones will __________ of smartphones. a) increase the supply b) increase the quantity supplied c) decrease the quantity supplied d) decrease the supply
Answers
Assuming everything else stays the same, an increase in the price of smartphones will decrease the quantity supplied of smartphones. Option c is the correct answer.
This is because the quantity supplied is the number of smartphones that suppliers are willing and able to sell at a given price, while supply refers to the entire range of quantities that suppliers are willing and able to sell at different prices.
When the price of smartphones increases, the cost of production and supply also increases. This leads to a decrease in the profitability of supplying smartphones at the current market price, and hence suppliers reduce the quantity supplied.
As a result, the quantity supplied of smartphones decreases, causing a leftward shift in the supply curve.
However, it is important to note that a decrease in the quantity supplied does not mean that there is a decrease in demand for smartphones. The demand for smartphones could remain the same, or even increase, leading to a shortage of smartphones in the market.
Therefore, the correct option is c.
To know more about supply refer to
https://brainly.com/question/28285610#
#SPJ11
A geometric sequence has a first term of 3 and a fourth term of 81÷8.
Find the eighth term
Answers
Answer:
6561 / 128
Step-by-step explanation:
The nth term of a geometric sequence is:
a = a₁ (r)ⁿ⁻¹
The first term is 3, and the fourth term is 81/8.
81/8 = 3 (r)⁴⁻¹
27/8 = r³
r = 3/2
The eighth term is therefore:
a = 3 (3/2)⁸⁻¹
a = 6561 / 128
Joseph has 150 animals on his farm. ⅕ of the animals are chickens, ⅕ of the animals are cows, and the rest of the animals are goats. How many goats does Joseph have on his farm?
Answers
Answer:
90 goats
Step-by-step explanation:
Number of chickens in farm = (1/5) of 150
= \(\frac{1}{5}*150\)
= 1 * 30
= 30
Number of cows in farm = \(\frac{1}{5}*150\)
= 1 * 30
= 30
Number of goats in farm = 150 - (30 + 30)
= 150 - 60
= 90
please help me
133÷3=?

Answers
Answer:
The answer is Forty Four Point Three recurring (44.3)
The points plotted below are on the graph of a polynomial. How many roots
of the polynomial lie between x = -4 and x = 3?
URGENT

Answers
Given:
The graph of a polynomial.
To find:
The number of roots of the polynomial lie between x = -4 and x = 3.
Solution:
From the given graph it is clear that the graph is a downward U-shaped curve. It means the given graph represents a quadratic polynomial.
The graph of the polynomial is below the x-axis immediate before x=-2 and above the x-axis immediate after x=-2. It means the graph intersect the x-axis at x=-2.
The graph of the polynomial is above the x-axis immediate before x=2 and below the x-axis immediate after x=2. It means the graph intersect the x-axis at x=2.
Since the graph of the polynomial divides the x-axis two times between x = -4 and x = 3, therefore the two roots of the polynomial lie between x = -4 and x = 3.
prove that (3-4sin^2)(1-3tan^2)=(3-tan^2)(4cos^2-3)
Answers
Answer:
Proof in the explanation.
Step-by-step explanation:
I expanded both sides as a first step. (You may use foil here if you wish and if you use that term.)
This means we want to show the following:
\(3-9\tan^2(\theta)-4\sin^2(\theta)+12\sin^2(\theta)\tan^2(\theta)\)
\(=12\cos^2(\theta)-9-4\cos^2(\theta)\tan^2(\theta)+3\tan^2(\theta)\).
After this I played with only the left hand side to get it to match the right hand side.
One of the first things I notice we had sine squared's on left side and no sine squared's on the other. I wanted this out. I see there were cosine squared's on the right. Thus, I began with Pythagorean Theorem here.
\(3-9\tan^2(\theta)-4\sin^2(\theta)+12\sin^2(\theta)\tan^2(\theta)\)
\(3-9\tan^2(\theta)-4(1-\cos^2(\theta))+12\sin^2(\theta)\tan^2(\theta)\(
Distribute:
\(3-9\tan^2(\theta)-4+4\cos^2(\theta)+12\sin^2(\theta)\tan^2(\theta)\)
Combine like terms and reorder left side to organize it based on right side:
\(4\cos^2(\theta)-1+12\sin^2(\theta)\tan^2(\theta)-9\tan^2(\theta)\)
After doing this, I since that on the left we had products of sine squared and tangent squared but on the right we had products of cosine squared and tangent squared. This problem could easily be fixed with Pythagorean Theorem again.
\(4\cos^2(\theta)-1+12\sin^2(\theta)\tan^2(\theta)-9\tan^2(\theta)\)
\(4\cos^2(\theta)-1+12(1-\cos^2(\theta))\tan^2(\theta)-9\tan^2(\theta)\)
Distribute:
\(4\cos^2(\theta)-1+12\tan^2(\theta)-12\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)\)
Combined like terms while keeping the same organization as the right:
\(4\cos^2(\theta)-1+3\tan^2(\theta)-12\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)\)
We do not have the same amount of the mentioned products in the previous step on both sides. So I rewrote this term as a sum. I did this as follows:
\(4\cos^2(\theta)-1+3\tan^2(\theta)-12\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)\)
\(4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)\)
Here, I decide to use the following identity \(\cos\theta)\tan(\theta)=\sin(\theta)\). The reason for this is because I certainly didn't need those extra products of cosine squared and tangent squared as I didn't have them on the right side.
\(4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8\cos^2(\theta)\tan^2(\theta)-9\tan^2(\theta)\)
\(4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8\sin^2(\theta)-9\tan^2(\theta)\)
We are again back at having sine squared's on this side and only cosine squared's on the other. We will use Pythagorean Theorem again here.
\(4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8\sin^2(\theta)-9\tan^2(\theta)\)
\(4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8(1-\cos^2(\theta))-9\tan^2(\theta)\)
Distribute:
\(4\cos^2(\theta)-1+3\tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)-8+8\cos^2(\theta)-9\tan^2(\theta)\)
Combine like terms:
\(12\cos^2(\theta)-9+3tan^2(\theta)-4\cos^2(\theta)\tan^2(\theta)\)
Reorder again to fit right side:
\(12\cos^2(\theta)-9+4\cos^2(\theta)\tan(\theta)+3\tan^2(\theta)\)
This does match the other side.
The proof is done.
Note: Reordering was done by commutative property.
(b) Find the greatest number that divides 300, 560 and 500 without leaving a remainder.
Answers
Greatest number that divides 300, 560 and 500 is 20 .
Given numbers : 300, 560 and 500
First let’s find prime factors of 300,560 and 500
300 = 2^2 *3^1 *5^2
560= 2^4 * 7^1 *5^1
500 = 2^2 * 5^3
So,
Here highest common power of 2 is 2
Here highest common power of 3 is 0
Here highest common power of 5 is 1
Here highest common power of 7 is 0
Thus HCF (300, 560 and 500) = 2^2 * 5^1 * 3 ^0 * 7 ^0
=4*5*1*1
= 20
Know more about HCF,
https://brainly.com/question/26431349
#SPJ1
Barney and Betty break into a parking meter with $3.90 in dimes and quarters in it (legal disclaimer: don't do this) and agree that Barney will get all the dimes, and Betty will get all the quarters. (Barley isn't terribly bright) Barney ends up with four more coins than Betty. How much money did each get(
Answers
Answer:
Barney got 14 dimes and Betty got 10 quarters.
Step-by-step explanation:
Since there are only dimes and quarters in the parking meter, the total money must be equal to:
\(0.1*dimes + 0.25*quarters = 3.9\)
Since Barney got all the dimes and he has four more coins than Betty, then the number of dimes is:
\(dimes = quarters + 4\)
Applying the second expression on the first, we have:
\(0.1*(quarters + 4) + 0.25*quarters = 3.9\\0.1*quarters + 0.4 + 0.25*quarters = 3.9\\0.35*quarters = 3.9 - 0.4\\0.35*quarters = 3.5\\quarters = \frac{3.5}{0.35} = 10\)
\(dimes = quarters + 4 = 10 + 4 = 14\)
Barney got 14 dimes and Betty got 10 quarters.
Find the inverse f(x)=6x+7
Answers
Answer:
\(f^{-1}\) (x) = \(\frac{x-7}{6}\)
Step-by-step explanation:
let y = f(x) , then rearrange making x the subject
y = 6x + 7 ( subtract 7 from both sides )
y - 7 = 6x ( divide both sides by 6 )
\(\frac{y-7}{6}\) = x
Change y back into terms of x with x = \(f^{-1}\) (x) , then
\(f^{-1}\) (x) = \(\frac{x-7}{6}\)
lacy wants to design an experiment that will show which part of a tomato flower grows into the tomato fruit. what measurement could she make to study how the fruit grows?
Answers
Lacy can measure the tomato fruit diameter, weight, length, and color to study how it grows.
To study how the fruit grows in a tomato flower, Lacy can make the following measurement:
1. Tomato Fruit Diameter: Lacy can measure the diameter of the tomato fruit at regular intervals to observe its growth over time. This can be done using a caliper or a ruler.
2. Fruit Weight: Lacy can weigh the tomato fruit using a scale to determine its growth. By comparing the weight of the fruit at different stages, she can observe how it increases over time.
3. Fruit Length: Lacy can measure the length of the tomato fruit using a ruler or measuring tape. This will provide insights into the fruit's growth in terms of its size and elongation.
4. Fruit Color: Lacy can observe and record the color changes in the tomato fruit as it grows. This can indicate the ripening process and the overall development of the fruit.
In conclusion, Lacy can measure the tomato fruit diameter, weight, length, and color to study how it grows. These measurements will provide valuable data to analyze the growth process and draw conclusions about which part of the tomato flower contributes to the fruit formation.
To know more about ripening process visit:
brainly.com/question/33813466
#SPJ11
what value of x will solve the equation 3/4x + 10 = 4
Answers
Answer:
-8
Step-by-step explanation:
Answer:
x = -8
Step-by-step explanation:
\(\frac{3}{4}x+10=4\)
\(\frac{3}{4} x-10\) \(-10\) Subtract 10 from both sides
\(\frac{3}{4}x=\) \(-6\)
\(\frac{3}{4}(-8)\) \(=-6\) Substitute x for \((-8)\) then Multiply \((-8)\) by \(\frac{3}{4}\)
\(-\frac{24}{4}\) \(=-6\) Simplify \(-\frac{24}{4}\)
\(-6=-6\)
in order to determine whether or not there is a significant difference between the hourly wages of two companies, two independent random samples were selected and the following statistics were calculated. company a company b sample size 80 60 sample mean $6.75 $6.25 population standard deviation $1.00 $0.95 refer to exhibit 10-8. the value of the test statistic is . a. 3.01 b. 1.645 c. 2.75 d. .098
Answers
The value of the test statistic is approximately 2.84. Its significance can't be determined.
To determine whether or not there is a significant difference between the hourly wages of two companies, we need to conduct a hypothesis test.
The null hypothesis states that there is no significant difference between the hourly wages of the two companies, while the alternative hypothesis states that there is a significant difference.
The test statistic for this hypothesis test is calculated using the formula:
\(t = (x1 - x2) / (s1^2/n1 + s2^2/n2)^(1/2)\)
where x1, x2 are the sample means for companies A and B, s1 and s2 are the sample standard deviations for companies A and B, and n1 and n2 are the sample sizes for companies A and B.
Plugging in given values, we get:
\(t = (6.75 - 6.25) / [(1^2/80) + (0.95^2/60)]^(1/2)\)
t = 0.5 / 0.1759
t = 2.8437
Without knowing the significance level or the degrees of freedom, we cannot determine whether or not the test statistic is statistically significant.
Learn more about test statistic here:
https://brainly.com/question/14128303
#SPJ11
The value of the test statistic is 2.75.
To determine the test statistic for comparing the hourly wages of two companies, the researcher would need to conduct a two-sample t-test with equal variances.
The formula for the test statistic is:
\(t = (\bar x1 - \barx2) / [s_p \times \sqrt(1/n1 + 1/n2)]\)
where:
\(\bar x1\) and\(\bar x2\) are the sample means for Company A and Company B, respectively
\(s_p\) is the pooled standard deviation of the two samples, calculated as:
\(s_p = sqrt [((n1 - 1) \times s1^2 + (n2 - 1) \times s2^2) / (n1 + n2 - 2)]\)
n1 and n2 are the sample sizes for Company A and Company B, respectively
s1 and s2 are the sample standard deviations for Company A and Company B, respectively.
Plugging in the given values, we get:
\(t = (6.75 - 6.25) / [\sqrt(((80-1)\times 1^2 + (60-1)\times 0.95^2)/(80+60-2)) \times \sqrt(1/80 + 1/60)]\)
\(t = 2.75\)
For similar questions on statistic
https://brainly.com/question/15525560
#SPJ11
Regular hexagon ABCDEF is inscribed in a circle with center H. What is the image of segment BC after 120 degree clockwise rotation about point H?
Answers
Regular hexagon ABCDEF is inscribed in a circle with center H, the image of segment BC after 120 degree clockwise rotation about point H is the segment joining the points B' and C', which has endpoints (-0.5r\(\sqrt{3\), -0.5r) and (-0.5r, -0.5r).
Since the hexagon is inscribed in a circle with center H, we can conclude that H is also the center of the circle passing through vertices B, C, and D. Therefore, the circle passing through B, C, and D is also a 120 degree clockwise rotation of the circle passing through A, B, and C.
To find the image of segment BC after a 120 degree clockwise rotation about point H, we need to find the coordinates of B and C relative to H, and then apply a 120 degree rotation matrix to these coordinates.
Let the radius of the circle be r, and let the coordinates of H be (0,0). Then the coordinates of B and C are:
B: (r cos(60), r sin(60))
C: (r cos(0), r sin(0)) = (r, 0)
To apply a 120 degree clockwise rotation matrix, we can use the following matrix:
[ cos(-120) -sin(-120) ]
[ sin(-120) cos(-120) ]
Simplifying, we get:
[ cos(120) sin(120) ]
[ -sin(120) cos(120) ]
Applying this matrix to the coordinates of B and C, we get:
B': [ cos(120) sin(120) ][ r cos(60) ] = [ -0.5r \(\sqrt{3}\)]
[ -sin(120) cos(120) ][ r sin(60) ] [ -0.5r ]
C': [ cos(120) sin(120) ][ r ] = [ -0.5r ]
[ -sin(120) cos(120) ][ 0 ] [ -0.5r ]
Therefore, the image of segment BC after a 120 degree clockwise rotation about point H is the segment joining points B' and C', which has endpoints (-0.5r\(\sqrt{3}\), -0.5r) and (-0.5r, -0.5r), respectively.
To know more about Hexagon:
https://brainly.com/question/2001860
#SPJ4
The solution set for -18 < 5x - 3 is ____.
3 > x
3 < x
-3 < x
-3 > x
Answers
Answer:
x > -3
Step-by-step explanation:
Isolate the x on the left:
-5x < -3 + 18
-5x < 15
-x < 3
x < -3
what is this pls help me

Answers
Answer:
distance would make the most sense
Answer:
Distance
it's because distance cannot be negative, always making it positive, or the absolute value.
Morris shovels driveways during a big snowstorm. He charges $25 to shovel a drive way. He can shovel a drive way in a half hour assuming that he worked back to back how much could he make in 5 hours
Answers
Answer:
250
Step-by-step explanation:
5 x 2= 10
25 x 10= 250
Someone help 100 points and marking brainliest
Answers
Answer:
ehh....130 is your answer alr bye
the answer to your question is 130
Solve the inequality -7x > 21. What is the graph of the solution
Answers
Answer:
Step-by-step explanation:
-7x > 21.
-x>3
x<-3

The answer is:
x < -3Work/explanation:
To solve the inequality, we should divide each side by -7.
Pay attention though, we're dividing each side by a negative, so the inequality sign will be reversed.
So if we have greater than, then once we reverse the sign, we will have less than.
This is how it's done :
\(\sf{-7x > 21}\)
Divide :
\(\sf{x < -3}\)
Therefore, the answer is x < -3 .what's the answer !!
\( \sqrt{44 \times 2 \times 2 \times 11} \)
Answers
Answer:
44
Step-by-step explanation:
\( \sqrt{44 \times 2 \times 2 \times 11} \)
\( \sqrt{88 \times 2 \times 11} \)
\( \sqrt{176 \times 11} \)
\( \sqrt{1936}\)
\( \sqrt{ {44}^{2} } \)
Pull terms out from under the radical, assuming positive real numbers.
\(44\)
Hope it is helpful.....Step-by-step explanation:
\( \sqrt{44 \times 2 \times 2 \times 11} \\ = \sqrt{11 \times 4 \times 4 \times 11} \\ = \sqrt{11 \times 11 \times 4 \times 4} \\ = 11 \times 4 \\ = 44\)
The pep squad is making mascot flags. They used 1.5 yards each of crimson, gold, and navy fabric to make 90 flags. How much fabric is needed to make 1 flag?
Answers
It will take 0.05 yards of fabric to make one flag.
What is a mathematical function, equation and expression?function : In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.expression : A mathematical expression is made up of terms (constants and variables) separated by mathematical operators.equation : A mathematical equation is used to equate two expressions.Given is that a pep squad is making mascot flags. They used 1.5 yards each of crimson, gold, and navy fabric to make 90 flags.
Assume that the total fabric needed is [x] yards. So -
(1.5 x 3) yards is needed to make 90 flags.
4.5 yards is need to make 90 flags.
1 flag will need (4.5/90) yards or 0.05 yards of fabric is needed.
Therefore, it will take 0.05 yards to make 1 flag.
To solve more questions on functions, expressions and polynomials, visit the link below -
brainly.com/question/17421223
#SPJ1
if 24 machines can make 5 devices in 30 minutes, how many hours will it take 4 machines to make 15 devices?
Answers
To solve this problem, we can set up a proportion based on the given information. Let's assume that the number of machines is directly proportional to the number of devices produced .
The time taken is inversely proportional to the number of devices produced. From the given information: 24 machines can make 5 devices in 30 minutes. let's assign variables: Let m1 be the number of machines.
Let d1 be the number of devices. Let t1 be the time taken. We have the following ratios: m1:d1 = 24:5 (number of machines to number of devices)
t1:d1 = 30:5 (time taken to number of devices). Now we need to find the time it would take for 4 machines to make 15 devices. Let m2 be the number of machines (4 in this case). Let d2 be the number of devices (15 in this case). Let t2 be the time taken (to be determined). We can set up the following proportion: m1:d1 = m2:d2. Substituting the values we have: 24:5 = 4:15. To find t2, we can set up the following proportion:
t1:d1 = t2:d2. Substituting the values we have: 30:5 = t2:15. Now we can solve for t2: 24/5 = 4/d2 (Cross-multiply). 24d2 = 4 * 5. 24d2 = 20. d2 = 20/24. d2 = 5/6. So, 4 machines will make 15 devices in 5/6 of the time it took 24 machines to make 5 devices. To find the time, we can set up a proportion: 30/5 = t2/(5/6) (Cross-multiply). 30 * (5/6) = t2. 25 = t2. Therefore, 4 machines will take 25 minutes to make 15 devices. To convert this to hours, divide the time by 60: 25 minutes = 25/60 hours
25/60 = 5/12(Answer) .
Therefore , if 24 machines can make 5 devices in 30 minutes, 4 machines will take 5/12 of an hour to make 15 devices.
To learn more about proportion click here: brainly.com/question/31548894
#SPJ11
how to determine magnitude of order
Answers
For some values, such as the speed of light or the separation between the Earth and the sun, scientists and mathematicians long ago realized they needed a simpler way to write and refer to these large numbers.
They developed/created scientific notation at that time.
For us to estimate the order of magnitude:
Firstly, write the number in scientific notation.
Secondly, Round up to the nearest integer times a power of ten or power of ten.
Thirdly, Apply these estimates to your calculations.
Fourthly, If possible, compare the result to the exact one.
Example question, How many orders of magnitude are there in one million, for instance?
Answer will be, In order to represent the number 1,000,000, we will move the decimal to the left, stopping just before the first digit. The order of magnitude is determined by the quantity of left moves you make. Since we moved it six times, there are six orders of magnitude between ten and one million, which means that ten times six is equal to one million.
To learn more about order of magnitude: https://brainly.com/question/30460426
#SPJ4
The area (A) of a triangle varies jointly as the base (b) and the height (h). The area
of a triangle whose height is 24 cm and whose base is 4 cm is 48 cm. Find the
area of a triangle of whose
height is 16 cm and base is 6 cm.
Answers
The area of triangle varies jointly as its base and height. Given that the area of a triangle with a height of 24 cm and a base of 4 cm is 48 cm, we can find the area of a triangle with a height of 16 cm and a base of 6 cm.
Let A represent the area of the triangle, b represent the base, and h represent the height. According to the given information, the area A varies jointly as the base b and the height h, which can be expressed as A = k * b * h, where k is a constant of variation.
We are given that when h = 24 cm and b = 4 cm, the area A is 48 cm. Substituting these values into the equation, we get 48 = k * 4 * 24. Simplifying this equation, we find that k = 1.
Now, we can use the value of k to find the area of the triangle when h = 16 cm and b = 6 cm. Plugging these values into the equation A = k * b * h, we get A = 1 * 6 * 16. Simplifying, we find that the area is 96 cm.
Therefore, the area of a triangle with a height of 16 cm and a base of 6 cm is 96 cm.
Learn more about area of triangle here:
https://brainly.com/question/29156501
#SPJ11
help me 2x-4y-3(7x-2y)
Answers
Let's simplify the above expression :
\(2x - 4y - 3(7x - 2y)\)\(2x - 4y - 21x + 6y\)\( - 19x + 2y\)Find the derivative of the following function:
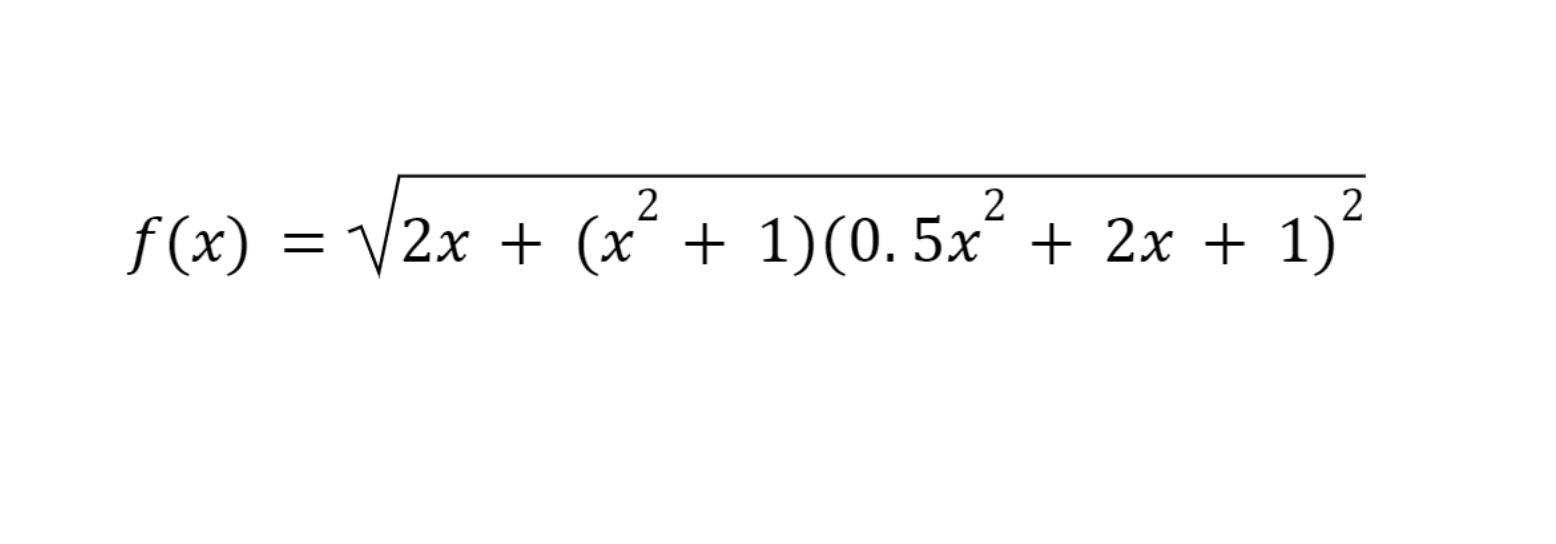
Answers
The derivative of the function \(f(x) = \sqrt{2x + (x^2 + 1) (0.5x^2 + 2x + 1)^2}\) will be given below.
\(f'(x) = \dfrac{1 + (0.5x^2 + 2x + 1)(1.5x^3 + 4x^2 + 2x + 2)}{\sqrt{2x + (x^2 + 1) (0.5x^2 + 2x + 1)^2}}\)
What is differentiation?The rate of change of a function with respect to the variable is called differentiation. It can be increasing or decrease.
The equation of the function will be given as,
\(f(x) = \sqrt{2x + (x^2 + 1) (0.5x^2 + 2x + 1)^2}\)
The derivative of the function will be given as,
\(f'(x) = \dfrac{d}{dx} \ \sqrt{2x + (x^2 + 1) (0.5x^2 + 2x + 1)^2} \\\\\\f'(x) = \dfrac{2 + 2(x^2 + 1)(0.5x^2 + 2x + 1) \cdot (x + 2) + (0.5x^2 + 2x + 1)^2 \cdot 2x}{2\sqrt{2x + (x^2 + 1) (0.5x^2 + 2x + 1)^2} }\\\\\\f'(x) = \dfrac{2 + (0.5x^2 + 2x + 1)[2(x^2 + 1)(x + 2) + (0.5x^2 + 2x + 1) \cdot 2x]}{2\sqrt{2x + (x^2 + 1) (0.5x^2 + 2x + 1)^2} }\\\)
Solve the equation further, then we have
\(f'(x) = \dfrac{1 + (0.5x^2 + 2x + 1)[(x^2 + 1)(x + 2) + (0.5x^2 + 2x + 1) \cdot x}{\sqrt{2x + (x^2 + 1) (0.5x^2 + 2x + 1)^2}}\\\\\\f'(x) = \dfrac{1 + (0.5x^2 + 2x + 1)(x^3 + 2x^2 + x + 2 + 0.5x^3 + 2x^2 + x)}{\sqrt{2x + (x^2 + 1) (0.5x^2 + 2x + 1)^2}}\\\\\\f'(x) = \dfrac{1 + (0.5x^2 + 2x + 1)(1.5x^3 + 4x^2 + 2x + 2)}{\sqrt{2x + (x^2 + 1) (0.5x^2 + 2x + 1)^2}}\)
More about the differentiation link is given below.
https://brainly.com/question/24062595
#SPJ1
Please help me!!!!!!!!!!

Answers
Answer:
it think it is D
Step-by-step explanation:
just take one of the number and move it for example 4x right and 2y up and then look at where the connection is.
