Answers
Answer:
92in²
Step-by-step explanation:
A= 1/2(b1+b2)h = 1/2 (18+5)8=
1/2 (23)8= 1/2 184 = 92in²
Related Questions
a tank initially contains 102 liters of pure water. brine containing 3 lb salt/liter begins to enter the tank at a rate of 1 liter/min and the well-mixed solution is drained at 2 liters/min. how much salt is in the solution after 10 minutes? (round your answer to two decimal places.)
Answers
To solve this problem, we need to consider the rate at which salt enters and leaves the tank over time.
First, let's calculate the amount of salt entering the tank during each minute. The brine entering the tank has a concentration of 3 lb salt per liter. Since the rate of brine entering the tank is 1 liter per minute, the amount of salt entering the tank per minute is 3 lb.
Next, let's determine the rate at which the solution is being drained from the tank. The solution is being drained at a rate of 2 liters per minute.
During each minute, the net increase in the amount of salt in the tank is given by the difference between the amount of salt entering and leaving the tank. In this case, it is 3 lb (entering) minus 2 lb (leaving) which equals 1 lb.
Therefore, the amount of salt in the tank increases by 1 lb per minute.
To find the total amount of salt in the tank after 10 minutes, we multiply the net increase per minute (1 lb) by the number of minutes (10):
Total amount of salt = 1 lb/minute * 10 minutes = 10 lb.
Therefore, after 10 minutes, there will be 10 lb of salt in the solution in the tank.
learn more about amount here
https://brainly.com/question/15701834
#SPJ11
True or false? for any propositional formula f, every stable model of f is a model of f
Answers
True, for any propositional formula f, every stable model of 'f' is a model of "f'.
A stable model is a type of logical model used in logic programming and non-monotonic reasoning. It is a set of logical sentences that are consistent with the propositional formula f and that satisfy certain stability conditions.
In other words, a stable model is a model of the propositional formula "f" that is also consistent with the additional constraints imposed by the stability conditions. Because of this, every stable model of f is also a model of 'f'.
Therefore, the statement "for any propositional formula f', every stable model of f is a model of f" is true.
To learn more about propositional formulas ,visit:
brainly.com/question/17137539
#SPJ11
Please help its urgent:
A bag contains one tile for each letter of the word PANDA. If you selected a permutation of these letters at random, what is the probability that they would spell the word panda?
Answers
Answer:
1/60Step-by-step explanation:
Permutations of "Panda"
5P5 = 5! = 120Two of the 'Panda" s we can get as a result
P(Panda) = 2/120 = 1/60Using Permutation
\(\boxed{\sf ^nP_r=n!}\)
\(\\ \sf\longmapsto ^5P_r=5!\)
\(\\ \sf\longmapsto 1\times 2\times 3\times 4\times 5\)
\(\\ \sf\longmapsto 120\)
Now
\(\\ \sf\longmapsto P(Panda)=\dfrac{2}{120}\)
\(\\ \sf\longmapsto P(Panda)=\dfrac{1}{60}\)
Find the length of the missing side


Answers
Answer: 13, 3.43
Step-by-step explanation:
Pythagorean theorem is:
c²=a²+b²
c is always the hypotenuse, the side that is longest or the side opposite of the right angle
a and b are the other 2 sides (for this it doesn't matter which is which
1. c=x a=12 b=5
x²=12²+5² 12² means (12)(12)=144 (12, 2 times)
x²=144+25 simplify by adding the numbers
x²=169 to solve for x take the √ of both sides
√x²=√169
x=13
2. c=10.1 b=9.5 a=x
10.1²=9.5²+x²
102.01=90.25 +x² subtract 90.25 from both sides
11.76=x² take square root of both sides to solve for x
√x²=√11.76
x=3.43
Answer: 13, 3.43
Step-by-step explanation:
Pythagorean theorem is:
c²=a²+b²
c is always the hypotenuse, the side that is longest or the side opposite of the right angle
a and b are the other 2 sides (for this it doesn't matter which is which
1. c=x a=12 b=5
x²=12²+5² 12² means (12)(12)=144 (12, 2 times)
x²=144+25 simplify by adding the numbers
x²=169 to solve for x take the √ of both sides
√x²=√169
x=13
2. c=10.1 b=9.5 a=x
10.1²=9.5²+x²
102.01=90.25 +x² subtract 90.25 from both sides
11.76=x² take square root of both sides to solve for x
√x²=√11.76
x=3.43
Graph the following features: Slope = -3 Y-intercept = -2/5
Answers
Answer:
Here is it graphed. The equation was:
y=-3x+-2/5
Step-by-step explanation:

The puzzle about each letter being 0-9, any ideas?
HANGER + HANGER + HANGER = ALGEBRA
Answers
The answer to the cryptarithmetic puzzle is HANGER = 920614
ALGEBRA = 2761842
A = 2 B = 8 E = 1 G = 6 H = 9 L = 7 R = 4
How to solveIn this puzzle, we are given that the letters of the alphabet represent digits 0-9.
We are tasked to find which digits correspond to the letters A, B, E, G, H, L, N, and R in the equation HANGER + HANGER + HANGER = ALGEBRA.
To solve this, we first realize that HANGER is a 6-digit word and ALGEBRA is a 7-digit word.
Therefore, H must be at least 3 and A can only be 1 or 2. After trying both cases, we find that A=2 and R=4.
Plugging these in and solving the equation, we find that HANGER=920614 and ALGEBRA=2761842.
Thus, we can conclude that A=2, B=8, E=1, G=6, H=9, L=7, and R=4.
Read more about puzzles here:
https://brainly.com/question/28994707
#SPJ1
In a cryptarithmetic puzzle, the digits 0–9 are represented with letters of the alphabet. Use your understanding of addition to find which digits go with the letters A, B, E, G, H, L, N, and R. HANGER + HANGER + HANGER = ALGEBRA example: T:2, W:1, O:5 then the word TWO is 215(two hundred fifteen), not 2+1+5
ind the limit of the sequence with the given nth term. an = (7n+5)/7n.
Answers
The limit of the sequence is 1. This means that as n gets larger and larger, the terms of the sequence get closer and closer to 1.
The limit of the sequence with the nth term an = (7n+5)/7n can be found by taking the limit as n approaches infinity.
To do this, we can divide both the numerator and denominator by n, which gives:
an = (7 + 5/n)/7
As n approaches infinity, 5/n approaches 0, and we are left with:
an = 7/7 = 1
Therefore, the limit of the sequence is 1. This means that as n gets larger and larger, the terms of the sequence get closer and closer to 1.
Know more about the limit here:
https://brainly.com/question/30339394
#SPJ11
PLEASE ASAP: The tennis club has 5 new members each member buys a racet and a tube of balls. If 6 racket cost $186.00 and 6 tubes of balls cost $27.00 how much do the 5 people pay for rackets and balls?
Answers
Answer:
Total cost is $177.50.
Step-by-step explanation:
Rackets:
Divide the cost for racket by 6 to find the cost per racket.
186÷6=31
Multiply 31 by 5 to find the cost for 5 rackets.
31×5=155
$155
Tubes of balls:
Divide 27 by 6 to find the cost per a tube of balls.
27÷6=4.50
Multiply 4.50 by 5 to find the cost for 5 tubes of balls.
4.50×5=22.50
$22.50
Add the amounts for rackets and tubes of balls to find the total cost.
155+22.50=177.50
The total cost is $177.50.
Hope this helps!
Expand & simplify 2 ( g + 5 ) − 2 ( g + 3 )
Answers
4
Step-by-step explanation:
2 ( g + 5 ) − 2 ( g + 3 ) = 2 ( g + 5 ) − 2 ( g + 3 )
= 2g + 10 - 2g - 6
= 2g -2g + 10 - 6
= 0 + 4
= 4
Would like a step by step answer

Answers
Answer:
x= -9
Step-by-step explanation:
2x+3y=-18
2x+3x0=-18
2x+0=-18
2x=-18
divide that by 2 then you get
-9
solve for y:
-1/2 = 3/8y
y=?
Answers
Answer:
y=-4/3
Step-by-step explanation:
Answer:
-4/3
Step-by-step explanation:
Question 14At his job, Tomas earns a commission plus an hourly wage. The function below describes the total dollar amount Tomas earns, based on the number of hours he works,f(h) = 250 +8.5hWhat is the hourly wage Tomas earns
Answers
Answer:
$8.50
Explanation:
Given the function f(h) that describes the total dollar amount Tomas earns, based on the number of hours he works:
\(f\mleft(h\mright)=250+8.5h\)When h=1, f(1)=250+8.5(1)=$258.5
When h=2, f(2)=250+8.5(2)=$267
Now:
\(f(2)-f(1)=267-258.5=8.5\)It means therefore that for every additional hour, Tomas earns $8.5.
The hourly wage Tomas earns is $8.5.
Now,
Find the distance between the two points rounding to the nearest tenth (if necessary).
(2,−4) and (7,8)
Answers
Answer:
d = 13
Step-by-step explanation:
First, the distance formula is needed:
\(d = \sqrt{(x_{2} - x_{1} )^{2} +(y_{2} - y_{1 })^{2} }\)
Next we assign the points
(2,-4) is point 1, (7,8) is point 2
\(d = \sqrt{(7 - 2 )^{2} +(8 - (-4))^{2} } \\d = \sqrt{5^{2} +12^{2} } \\d = \sqrt{25 + 144}\\ d = \sqrt{169} \\d = 13\)
Given two points (2,-4) and (7,8)
To find - The distance between given points.
We know the formula that is used to find the distance is given as
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
We let P = (2,-4)
and Q = (7,8)
\(x_1=2, y_1=-4\\x_2=7,y_2=8\)
on substituting we get
\(d=\sqrt{(7-2)^2+(8+4)^2}\\ d=\sqrt{(5)^2+(12)^2} \\d=\sqrt{25+144} \\d=\sqrt{169}\\ d=13\)
Hence we get the distance between (2,-4) and (7,8) is 13.
Final answer - The distance is 13.
h(x) = x^2 - 4 - x
g(x) = 3x - 2
Find h(x) division sign g(x)
Answers
Answer:
g(x)=x
4
+3x
3
−x
2
−3x
Step-by-step explanation:
in the xy-plane, which of the following is an equation of a vertical asymptote to the graph Of y=sec(6x-pi)? (A) x=pi/6 (B) x=pi/4 (C) x=pi/3 (D)=x=pi/2 (E) x=pi
Answers
The equation of a vertical asymptote to the graph of y = sec(6x - π) is x = π/6. Hence, option a is correct.
The function y = sec(6x - π) has vertical asymptotes at the values of x where the denominator of sec(6x - π) becomes zero. The reciprocal of sec(θ) is cos(θ). Because the cosine function has the values π/2, 3π/2, 5π/2, we will insert such an input that we get 0 in denominator.
6x - π = π/2
Solving for x,
6x = π/2 + π
6x = 3π/2
x = (3π/2) / 6
x = π/6
Therefore, the equation of a vertical asymptote to the graph of y = sec(6x - π) is x = π/6.
To know more about asymptotes, visit,
https://brainly.com/question/4138300
#SPJ4
Triangle ADE is similar to triangle ABG. Which of the following statements must be
true
PLEASE HELP ASAP
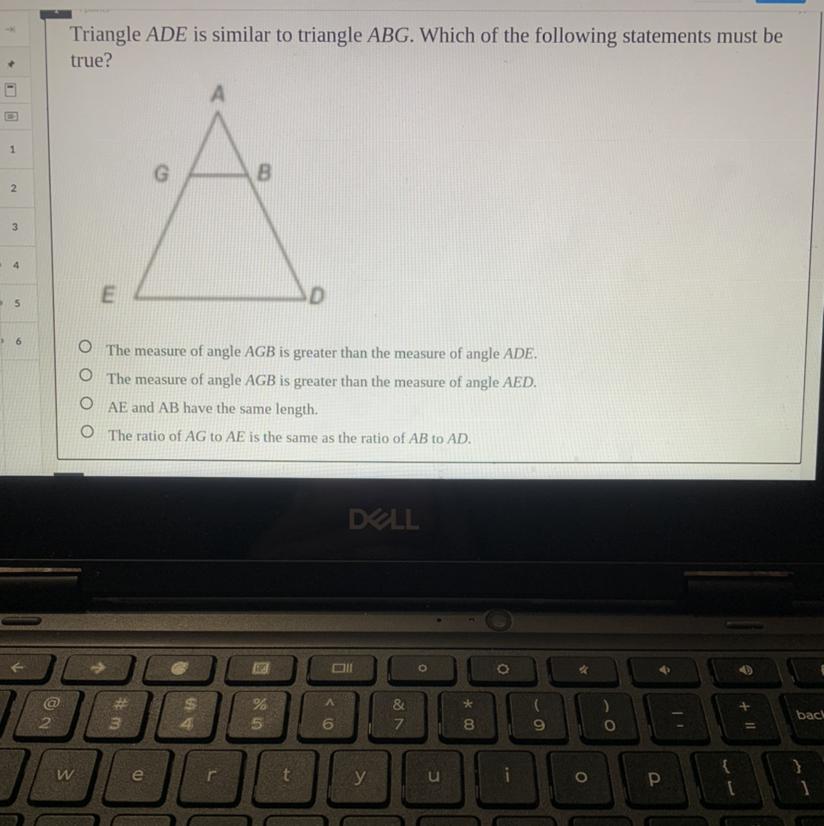
Answers
The perimeter of a rectangular roof shingle is 46 inches. It is 13 inches long. How wide is it?
inches
(Help please)
Answers
Answer:
8.5 in
Step-by-step explanation:
step 1
to find the width, the equation would be:
P/2-L
step 2-plug in
43/2-13=
8.5
Answer:
Step-by-step explanation: 10 + 10 = 20
46 - 20 = 26
26 divided by 2 = 13
Find the radius of convergence, \( R \), of the series. \[ \sum_{n=1}^{\infty} \frac{x^{8 n}}{n !} \] \[ R= \] Find the interval, I, of convergence of the series. (Enter your answer using interval notation.) I=
Answers
The series \(\(\sum_{n=1}^{\infty} \frac{x^{8n}}{n!}\)\) converges for all real values of \(\(x\)\), and the interval of convergence, \(\(I\)\), is the entire real number line, represented by \(\(I = (-\infty, \infty)\).\)
To find the radius of convergence, \(\( R \),\) of the series \(\(\sum_{n=1}^{\infty} \frac{x^{8n}}{n!}\),\) we can use the ratio test.
The ratio test states that for a power series \(\(\sum_{n=1}^{\infty} a_n(x-a)^n\)\) , if the limit \(\(L = \lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right|\)\) exists, then the radius of convergence is given by \(\(R = \frac{1}{L}\).\)
In this case, \(\(a_n = \frac{1}{n!}\) and \(a_{n+1} = \frac{1}{(n+1)!}\).\)
Let's calculate the ratio:
\(\[L = \lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right| = \lim_{n \to \infty} \left|\frac{\frac{1}{(n+1)!}}{\frac{1}{n!}}\right| = \lim_{n \to \infty} \left|\frac{n!}{(n+1)!}\right| = \lim_{n \to \infty} \frac{1}{n+1} = 0\]\)
Since the limit \(\(L = 0\), we have \(R = \frac{1}{L} = \frac{1}{0}\),\) which means that the radius of convergence is infinite \((\(R = \infty\)).\)
Therefore, the series \(\(\sum_{n=1}^{\infty} \frac{x^{8n}}{n!}\)\) converges for all real values of \(\(x\)\), and the interval of convergence, \(\(I\)\), is the entire real number line, represented by \(\(I = (-\infty, \infty)\).\)
To know more about infinite visit-
brainly.com/question/32525213
#SPJ11
1. Please help if possible :)

Answers
Answer:
54
Step-by-step explanation:
6x=9x-27
x=9
9*9-27=54
solve the equation
pic:

Answers
The solution to the equation \((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\) is 10.3891
How to solve the equationFrom the question, we have the following parameters that can be used in our computation:
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\)
Using the following trigonometry ratio
sin²(x) + cos²(x) = 1
We have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = (\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + 1 + e^2\)
The sum to infinity of a geometric series is
S = a/(1 - r)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = \frac{1/2}{1 - 1/2} + \frac{9/10}{1 - 1/10} + 1 + e^2\)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 1 + 1 + 1 + e^2\)
Evaluate the sum
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 3 + e^2\)
This gives
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 10.3891\)
Hence, the solution to the equation is 10.3891
Read more about summation notation at
brainly.com/question/15973233
#SPJ1
Give your answer as a fraction,or accurate at least 4 decimal places

Answers
Given:
Shannon buys a bag of cookies that contains 6 chocolate chip cookies, 7 peanut butter cookies, 4 sugar cookies and 6 oatmeal cookies.
Required:
To find the probability that Shannon reaches in the bag and randomly selects a oatmeal cookies from the bag, eats it, then reaches back in the bag and randomly selects a chocolate chip cookies.
Explanation:
There are total 23 cookies.
P(select oatmeal cookies from the bag, eats it, then reaches back in the bag and randomly selects a chocolate chip cookies.) =
\(\begin{gathered} =(\frac{6}{23})\times(\frac{6}{22}) \\ \\ =\frac{36}{506} \\ \\ =0.07114 \end{gathered}\)Final Answer:
The proba0.0711
What is the length of EF in the right triangle below? A. 168 B. /324 C. 24 D. 18 E. 527 F. 32

Answers
Answer: C 24
Step-by-step explanation:
The measure of the length of EF in a right-angle triangle is 24 units, then the correct option is C.
What is a right-angle triangle?It is a type of triangle in which one angle is 90 degrees and it follows the Pythagoras theorem and we can use the trigonometry function. The Pythagoras is the sum of the square of two sides is equal to the square of the longest side.
The right-angle triangle is shown in a diagram. Then by the Pythagoras theorem, we have
P² = H² - B²
P² = 25² - 7²
P² = 625 - 49
P² = 576
P = 24
More about the right-angle triangle link is given below.
https://brainly.com/question/3770177
1. If f(x)= 3r? - 7x+15, then lf(-2)=
a. -7
b. 65
c. 0
D. 42
E. none of the above.
Answers
Answer:
E. None of the above
Hope you could understand.
If you have any query, feel free to ask.
A number has exactly 8 factors, two of which are 4 and 20. List all the factors of the number.
Answers
The number in question is 4*20 = 80.
The factors of 80 are:
1, 2, 4, 5, 8, 10, 16, 20, 40 and 80
A factor of a number is an integer that divides the number completely without leaving a remainder. To find the factors of 80, we can start with 1 and divide 80 by each number up to 80. Any number that divides 80 without leaving a remainder is a factor of 80.
1, 2, 4, 5, 8, 10, 16, 20, 40 and 80 are the factors of 80.
You have a sample of 10 household incomes. Based on this sample what fraction of households can you expect to Earn between 75,000$ and 100,000$?
$33,000 $108,000 $85,000 $41,000 $85,000 $105,000 $96,000 $107,000 $116,000 $18,000
Answers
The correct fraction of households that can be expected to earn between $75,000 and $100,000 is 3/10, or 0.3 (30%).
To determine the fraction of households that can be expected to earn between $75,000 and $100,000 based on the given sample, we need to count the number of incomes within that range and divide it by the total number of incomes in the sample.
From the given sample of 10 household incomes:
$33,000, $108,000, $85,000, $41,000, $85,000, $105,000, $96,000, $107,000, $116,000, $18,000
We can see that there are 3 incomes within the range of $75,000 and $100,000, which are $85,000, $85,000, and $96,000.
Therefore, the fraction of households that can be expected to earn between $75,000 and $100,000 is 3/10, or 0.3 (30%).
Learn more about statistics here:
https://brainly.com/question/30915447
#SPJ11
On a coordinate plane, square p q r s is shown. point p is at (4, 2), point q is at (8, 5), point r is at (5, 9), and point s is at (1, 6). which statement proves that the diagonals of square pqrs are perpendicular bisectors of each other? the length of sp, pq, rq, and sr are each 5. the slope of sp and rq is negative four-thirds and the slope of sr and pq is three-fourths. the length of sq and rp are both startroot 50 endroot. the midpoint of both diagonals is (4 and one-half, 5 and one-half), the slope of rp is 7, and the slope of sq is negative one-sevenths.
Answers
A statement which proves that the diagonals of square PQRS are perpendicular bisectors of each other is: option D.
How to calculate the slope of a line?Mathematically, the slope of a line is given by the following formula;
\(Slope = \frac{Change\;in\;y\;axis}{Change\;in\;x\;axis}\\\\Slope = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}\)
For line RP, we have:
\(Slope = \frac{9\;-\;2}{5\;-\;4}\\\\Slope = \frac{7}{1}\)
Slope RP = 7.
For line SQ, we have:
\(Slope = \frac{6\;-\;5}{1\;-\;8}\\\\Slope = \frac{1}{-7}\)
Slope SQ = negative one-sevenths.
For the midpoint, we have:
In order to determine the midpoint of a line segment with two (2) endpoints, we would add each point together and divide by two (2).
Midpoint on x-coordinate = (8 + 1)/2 = 9/2 = 4.5.
Midpoint on y-coordinate = (9 + 2)/2 = 11/2 = 5.5.
In conclusion, a statement which proves that the diagonals of square PQRS are perpendicular bisectors of each other is that the midpoint of both diagonals is (4.5, 5.5), the slope of RP is 7, and the slope of SQ is negative one-sevenths.
Read more on squares here: https://brainly.com/question/2882032
#SPJ4

Answer:
D. The midpoint of both diagonals is (4 1/2, 5 1/2) , the slope of RP is 7, and the slope of SQ is - 1/7.
Step-by-step explanation: I just did it on edge 2023. Hope this helps!

1
y = -x - 7
2
How do I graph that?
Answers
here is the graph for 1 y = -x - 7 2

Answer:
Slope: \(-1\)
y-intercept: \((0,72)\)
Step-by-step explanation:
\(1y=-x-72\)
Look down below for graph.
Hope this helps!

Suppose that a linear system of equations in unknowns x, y, and z has the following augmented matrix.
Use Gauss-Jordan elimination to solve the system for x, y, and z.
Answers
Given a linear system of equations in unknowns x, y, and z with the following augmented matrix:{[1, -1, 0, 0, -7], [-2, 3, 0, 0, 2], [0, 0, 4, -2, 2]}Use Gauss-Jordan elimination to solve the system for x, y, and z.Solution:Step 1. The first step in solving this linear system of equations is to write the matrix in the form of an augmented matrix. In the following, we list the system of equations associated with the augmented matrix: 1x−1y=−72x+3y=24z−y=1 We begin by focusing on the first equation, which is:1x−1y=−7.
To get rid of the x-coefficient, we add one time the first equation to the second equation. This operation is written as follows:{[1, -1, 0, 0, -7], [-2, 3, 0, 0, 2], [0, 0, 4, -2, 2]}We add row1 to row2. -2r1 + r2 = r2{-2, 2, 0, 0, 14}r3 = r3This gives us the new augmented matrix.{[1, -1, 0, 0, -7], [0, 1, 0, 0, -5], [0, 0, 4, -2, 2]}Step 2Next, we focus on the second equation:0x+1y=−5.
The y-variable is isolated, and we now look at the third equation.4z−2y=1We can isolate the variable z by dividing the entire equation by 4 as follows:z−0.5y=0.25In order to eliminate y in the third row, we add 0.5 times the second row to the third row. This operation is written as follows:{[1, -1, 0, 0, -7], [0, 1, 0, 0, -5], [0, 0, 4, -2, 2]}We add 0.5 r2 to r3. r3 + 0.5r2 = r3{[1, -1, 0, 0, -7], [0, 1, 0, 0, -5], [0, 0, 4, -1, -1]}Step 3We can now solve for z using the third equation:4z−1y=−1z = (-1 + y) / 4.
Substituting this into the second equation gives:-2((1 - y) / 4) + 3y = 2y - 1 = 2y - 1Thus, y = 1/2.Substituting the value of y = 1/2 into the first equation gives:x - (1/2) = -7, so x = -13/2.Finally, we can substitute the values of x and y into the third equation to get the value of z: 4z - 1(1/2) = -1, so z = -3/2.The solution to the system of linear equations is: x = -13/2, y = 1/2, and z = -3/2.
Learn more about linear system of equations:
https://brainly.com/question/13729904
#SPJ11
The diameter of a circular pizza is 24 in. How much pizza is eaten (in square inches) if half of it is consumed? (Pie and л... hmmmm...interesting...)
Answers
Using the formula of area of a circle, about 226.08in² has been eaten
How much pizza is eaten?The diameter of the pizza is given as 24 inches. To calculate the area of the entire pizza, we need to use the formula for the area of a circle:
Area = π * r²
where π is approximately 3.14 and r is the radius of the circle.
Given that the diameter is 24 inches, the radius (r) would be half of the diameter, which is 12 inches.
Let's calculate the area of the entire pizza first:
Area = 3.14 * 12²
Area = 3.14 * 144
Area ≈ 452.16 square inches
Now, if half of the pizza is consumed, we need to calculate the area of half of the pizza. To do that, we divide the area of the entire pizza by 2:
Area of half of the pizza = 452.16 / 2
Area of half of the pizza ≈ 226.08 square inches
Therefore, if half of the pizza is consumed, approximately 226.08 square inches of pizza would be eaten.
Learn more on area of a circle here;
https://brainly.com/question/15673093
#SPJ1
In ΔSTU, m∠S=(11x+3)∘,∠T=(2x+16)∘, and m∠U=(x+7)∘. Find .
Answers
Answer:
x = 11
Step-by-step explanation:
In ΔSTU ,
m∠S = (11x+3)° ; m∠T = (2x+16)° ; m∠U = (x+7)°
According to angle sum property of a triangle , sum of all the interior angles of the triangle is 180°.
So,
\(11x + 3 + 2x + 16 + x + 7 = 180\)
\( = > 14x + 26 = 180\)
\( = > 14x = 180 - 26 = 154\)
\( = > x = \frac{154}{14} = 11\)
