How many solutions does the equation have?

y+7=y–3

Responses

no solutions
no solutions

1 solution
1 solution

many solutions

The proportion of test takers scored between 6.5 and 8.0 is: P(6.5 <X< 8.0) = 0.218

In this question we have been given that the scores on the biology portion of the mcat are normally distributed with mean 8.0 and standard deviation 2.6

We need to find the proportion of test takers scored between 6.5 and 8.0

We know that the formula for z score is:

z = (X – μ) / σ

where X is the sample value, μ is the mean value and σ is the standard deviation

Here,  μ = 8.0

and σ = 2.6

when X = 6.5

z1 = (6.5 – 8.0) / 2.6

z1 = -0.57692

Using the standard distribution tables, proportion is P1 =  0.282

when X = 8.0

z2 = (8.0 – 8.0) / 2.6

z2 = 0

Using the standard distribution tables, proportion is P2 = 0.5

Therefore the proportion between X of 70 and 130 is:

P(6.5 <X< 8.0) = P2 – P1

P(6.5 <X< 8.0) = 0.5 -  0.282

P(6.5 <X< 8.0) = 0.218

Therefore, the required proportion is 0.218

Learn more about normal distribution here;

https://brainly.com/question/29509087

#SPJ4

Answer:

5).

According to the question,

CD+DE=CE

2+13=2x-3

15=2x-3

15+3=2x

18=2x

18/2=x

8=x

6).

According to the question,

AB+BC=AC

5x-16+3x-6=2x+20

8x-22=2x+20

8x-2x=20+22

6x=44

x=44/6

x=7.33

Step-by-step explanation:

......

Step-by-step explanation:

DE = 13

2 + 2x - 3 = 13

2x - 1 = 13

2x = 12

x = 12/2

x = 6

Answer: there is no answer

Step-by-step explanation: if the whole sentence is letters it is not answerable

A sample statistic can be described as a numerical value for a specific characteristic of a sample, which is a subset of a larger population.

A sample statistic is a numerical measure that describes a characteristic or property of a sample. It is a summary of the data collected from a sample and is used to make inferences about the population from which the sample was drawn. Sample statistics can include measures such as mean, median, mode, standard deviation, variance, and correlation coefficients. These statistics provide information about the central tendency, variability, and relationship between variables in the sample.

Sample statistics are used to estimate the population parameters, which are the numerical measures that describe the entire population. It is not feasible to collect data from the entire population, so we collect data from a representative sample and use the sample statistics to make inferences about the population parameters. The accuracy of the inferences depends on the sample size, sampling method, and the representativeness of the sample.

In summary, a sample statistic is a numerical measure that describes the characteristics of a sample and is used to make inferences about the population parameters. It provides important information about the sample and can help us to draw conclusions about the population from which the sample was drawn.

To learn more about statistic, click here:

https://brainly.com/question/31538429

#SPJ11

f(x) = x is a simple linear function with a slope of 1, f(x) = 3 5 6 is a constant function, f(x) = 3-x is a linear function with a negative slope of -1,  f(x) = 1 is a constant function, f(x) = 2 is a constant function

A constant function is a mathematical function whose output value is the same for every input value

From the given parameters, f(x) = x is a simple linear function with a slope of 1, this implies  that for every unit increase in x, the value of y increases by 1.

Also,  f(x) = 3 5 6 is a constant function, where the value of y is always 3 5 6, regardless of the value of x.

In the same way,  f(x) = 3-x is a linear function with a negative slope of -1, which means that for every unit increase in x, the value of y decreases by 1. The fourth function f(x) = 1 is a constant function, where the value of y is always 1, regardless of the value of x.

The domain of the fifth function is 3 0, which means that x can take any value between 3 and 0.

The sixth function f(x) = 2 is a constant function, where the value of y is always 2, regardless of the value of x.

Learn more about domain of a function on https://brainly.com/question/28599653

#SPJ1

Answer:

D. 800 m

Step-by-step explanation:

Volume of a cylinder is πr²h

Here, r=10 h=8

so the volume is

=π x 10² x8

=π x 100 x 8

=800m

The answer is 800m

Answer:

\(D\)

Step-by-step explanation:

\(Volume\)  \(of\) \(cylinder\) ≈ \(\pi\) \(radius^{2}\) × \(height\)

\(Volume\)  ≈ \(\pi\) × \(10^{2}\) × 8 \(800\pi\)

\(so\) \(it\) \(is\) \(D\)

Based on the given graph, the domain of the function can be expressed as [-5, 2], indicating that the function is defined for x-values within this interval.

Therefore, based on the given graph, the domain of the function can be expressed as [-5, 2], indicating that the function is defined for x-values within this interval.

For more questions on domain of the function:

https://brainly.com/question/28934802

#SPJ8

Answer:

$4.54

Step-by-step explanation:

7.7%=0.077

58.95*.077=$4.53915

$4.54

Answer:

A

Step-by-step explanation:

(f(-3+h)-f(-3))/h=(5(-3+h)^2-5(-3)^2)/h=(5*(-3+h-3)(-3+h+3))/h=-30*h/h=-30

In school suspension

Answer:

about $0.20

Step-by-step explanation:

44.75/225=0.20

Hopes this helps please mark brainliest

Answer:

The answer is b

Step-by-step explanation:

The distance traveled by the passenger train and the cattle train is equal to the total distance between them, which is 960 miles. Let x be the time (in hours) traveled by the passenger train and cattle train. Then, the equation that represents this situation is:

55x + 65x = 960

Simplifying the left-hand side of the equation, we get:

120x = 960

Dividing both sides by 120, we get:

x = 8

Therefore, the correct equation is:

B - 65x - 55x = 960

Answer:

what do you need help with

Step-by-step explanation:

Answer:

SAME

Step-by-step explanation:

I am so happy someone else goes through this! I'm SO happy I'm not alone.

The statement which is true is the airplane reaches its maximum height of 81 feet in 12 seconds.

Since the height of the plane is a function given by a parabola, we need to know the equation of a parabola in vertex form

The equation of a parabola with vertex (h,k) is given by y = a(x - h) + k

Since the height (in feet) of the airplane as a function of time (in seconds after the timer was started) is given by the equation h(t) = −(t − 12) + 81

So, the statement which is true is the airplane reaches its maximum height of 81 feet in 12 seconds.

Learn more about equation of a parabola in vertex form here:

https://brainly.com/question/17684824

#SPJ1

When using the elimination method to find a general solution for the given linear system, the differentiation is with respect to t, at a.  \(C . 1 e^{-2} t + C^{2}  e^6t\)

The given linear system is x' = 2x-yy' = 2y-16x

To solve this problem by the elimination method, we eliminate x and solve the remaining differential equation for y.x' = 2x-yy' = 2y-16x

Differentiate the first equation with respect to t is 2x'-y' = 2x''

Differentiate the second equation with respect to t is 2y'-16x' = 2y''

Substitute the value of x' from the first equation to the second equation is 2y'-16(2x-y) = 2y''y''-4y'+8x = 0

This is a homogeneous linear differential equation with constant coefficients. The characteristic equation is \(r^2\)-4r+8 = 0

Using the quadratic formula r = -b ± √(\(b^2\) - 4ac)/2a= 2 ± √(-12)/2= 2 ± 2i

We can now write the general solution y(t) = \(C . 1 e^{-2}  t cos 2t + C . 2 e^{-2}t\) sin 2t = \(C . 1 e^{-2} t + C^{2}  e^6t\)

Therefore, option a is the correct answer.

Know more about the Elimination method here :

https://brainly.com/question/28405823

#SPJ11

The correct  equation of the hyperbola is \((x + 1)^2 - (y - 8)^2 / 15 = 1.\)

To find the equation of a hyperbola given its foci and vertices, we can use the standard form equation:

\((x - h)^2 / a^2 - (y - k)^2 / b^2 = 1\)

Where (h, k) represents the center of the hyperbola, a is the distance from the center to each vertex (also known as the semi-major axis), and b is the distance from the center to each asymptote (also known as the semi-minor axis).

In this case, the center of the hyperbola is at (-1, 7) and (-1, 9). Since the x-coordinate remains constant, we can conclude that the hyperbola is vertical, and the center is at (-1, 8).

The distance between the center and each vertex is a = (9 - 8) = 1.

The distance between the center and each focus is c = (12 - 8) = 4.

To find the value of b, we can use the relationship between a, b, and c in a hyperbola: \(c^2 = a^2 + b^2.\)

Substituting the known values, we have:

\(4^2 = 1^2 + b^2\)

\(16 = 1 + b^2\)

\(b^2 = 16 - 1\)

\(b^2 = 15\)

b = √15

Now, we can write the equation of the hyperbola:

\((x - h)^2 / a^2 - (y - k)^2 / b^2 = 1\)

\((x + 1)^2 / 1^2 - (y - 8)^2 / (\sqrt{15} )^2 = 1\)

\((x + 1)^2 - (y - 8)^2 / 15 = 1\)

Therefore, the equation of the hyperbola is \((x + 1)^2 - (y - 8)^2 / 15 = 1.\)

Learn more about hyperbola here:

https://brainly.com/question/30281625

#SPJ11

The nominal annual rate compounded semi-annually was earned on the investment if the balance was $543.70 in eight years is 14.024%.

Juana deposited $200 into a savings account that compounds interest semi-annually.

To find out the nominal annual rate compounded semi-annually was earned on the investment if the balance was $543.70 in eight years, use the formula for compound interest.

Compound Interest Formula The formula for compound interest can be expressed as shown below;

A=P(1+(r/n))^nt

Where; A = Final amount of money after t years

P = Principal amount of money

r = Annual nominal interest rate

n = Number of times the interest is compounded per year

t = Number of years

For Juana's investment, we have the following details

;P = $200A

= $543.70r

= ?n

= 2 (since the interest is compounded semi-annually)

In 8 years, the interest will be compounded 16 times since the interest is compounded semi-annually.

Therefore; t = 8 years

n = 2 × 8

= 16

Substituting the values into the formula and solving for the nominal annual rate gives;

A=P(1+(r/n))^nt543.7

= 200(1+(r/2))^16r/2

= 16√(543.7/200-1)r/2

= 0.03506r

= 0.07012Nominal annual rate

= 2 × 0.07012

= 0.14024 or 14.024%.

To know more about rate visit:

https://brainly.com/question/25565101

#SPJ11

Answer:

10 hours

Step-by-step explanation:

Amount paid= material fee + ($8)(number of hours worked)

Let the number of hours the plumber worked be t.

$107= $27 +$8t

107 -27= 8t

80= 8t

8t= 80

Divide both sides by 8:

t= 80 ÷8

t= 10

Thus, the plumber worked for 10 hours.

The correct format of the question is

If f(x)= \(\frac{1}{3}x^3 -4x^2+12x -5\) and the domain is the set of all x such that 0≤x≤9 , then the absolute maximum value of the function f occurs when x is

Answer:

The absolute maximum value of the function F(x) occurs when x is 9

Step-by-step explanation:

F'(x) = \(x^2 -8x +12= 0\)

      = (x-6)(x-2) = 0

      x = 2,6

so we have boundary points 0 , 9 and 2,6

The value of function at these four points

  x =     0    2       6     9

F(x) =  -5    17/3   -5     22

So the absolute maximum value of the given function is x = 9 and F(x) is 22.

The absolute maximum value of the function f occurs when x is 9 and this can be determined by differentiating f(x) and then equating it to zero.

Given :

In order to determine the absolute maximum value of function f(x), differentiate f(x) and then equate it to zero.

\(\rm f'(x)=\dfrac{1}{3}\times(3x^2)-8x+12\)

Now, equate the above equation to zero.

\(x^2-8x+12 = 0\)

Factorize the above quadratic equation.

\(x^2-6x-2x+12=0\)

x(x - 6) - 2(x - 6) = 0

(x - 6)(x - 2) = 0

Now, determine the value of f(x) at x = 0, 2, 6, 9

f(0) = -5

f(2) = 1/3.(8) - 4(4) + 12(2) - 5

f(2) = 17/3

f(6) = 72 - 144 + 72 - 5

f(6) = -5

f(9) = 243 - 324 + 108 - 5

f(9) = 22

So, the absolute maximum value of the function f occurs when x is 9.

For more information, refer to the link given below:

https://brainly.com/question/24898810

A positively skewed distribution is due to an extremely large number.

A positively skewed distribution is a type of distribution in which the majority of the data values are clustered towards the left side of the distribution, with a tail extending to the right. This means that there are relatively more smaller values in the dataset than larger values. In a positively skewed distribution, the mean of the dataset is typically larger than the median, and the mode may not be a good representation of the central tendency of the data. This is because the presence of a long tail on the right-hand side of the distribution pulls the mean towards the higher values, while the median remains closer to the center of the dataset. Some common examples of positively skewed distributions include income distributions, where there are a few extremely high earners that skew the data towards the right, and test scores, where there may be a few students who perform extremely well and pull the average higher than the median.

Here,

A positively skewed distribution occurs when the tail of the distribution extends to the right, and the majority of the data is clustered towards the left side of the graph. This means that there are relatively more smaller values in the dataset than larger values. One common cause of positive skewness is the presence of extremely large values, also called outliers, in the dataset. These large values pull the mean of the dataset towards the right, resulting in the tail of the distribution stretching in that direction.

Therefore, out of the options provided, the correct answer is "an extremely large number."

To know more about positively skewed distribution,

https://brainly.com/question/14503886

#SPJ1

Answer:

5y + 4

Step-by-step explanation:

-4y + 7 + 9y - 3

Subtract: 9y - 4y

5y + 7 - 3

Subtract: 7 - 3

5y + 4

Hope this helps and pls do mark me brainliest if you can:)

The probability that the mean weight of the 17 fruits will be between 489 grams and 500 grams is approximately 0.0322 - 0.0322 = 0.0000 (rounded to four decimal places).

The probability that the mean weight of 17 randomly picked fruits falls between 489 grams and 500 grams can be calculated using the Central Limit Theorem.

The mean weight of the 17 fruits will follow a normal distribution with a mean equal to the population mean (494 grams) and a standard deviation equal to the population standard deviation divided by the square root of the sample size (√17).

First, we calculate the z-scores for the lower and upper bounds:

Lower z-score:

z_lower = (489 - 494) / (8 / √17)

Upper z-score:

z_upper = (500 - 494) / (8 / √17)

Then, we use a standard normal distribution table or a calculator to find the probabilities associated with these z-scores. The probability that the mean weight falls between 489 grams and 500 grams is equal to the difference between these two probabilities.

Let's calculate the probabilities:

z_lower = (489 - 494) / (8 / √17) ≈ -1.8409

z_upper = (500 - 494) / (8 / √17) ≈ 1.8409

Using a standard normal distribution table or a calculator, we find that the probability corresponding to z_lower is approximately 0.0322 and the probability corresponding to z_upper is also approximately 0.0322.

The problem presents a normal distribution of fruit weights, with a given mean of 494 grams and a standard deviation of 8 grams. When we randomly select a sample of 17 fruits, the mean weight of this sample will also follow a normal distribution. According to the Central Limit Theorem, as the sample size increases, the distribution of the sample mean approaches a normal distribution, regardless of the shape of the population distribution.

In this case, since the range is relatively narrow and the sample size is moderate, the probability of the mean weight falling between 489 grams and 500 grams is quite low, approximately 0.0000.

Learn more about probability here:

https://brainly.com/question/31828911

#SPJ11

The book value of the building in 2014 was $3.96 million. The book value of the building in 2028 will be $2.28 million.

a) The book value of the building in 2014 can be calculated as follows:

Book Value = Original Cost - (Depreciation Rate * Years Depreciated)

Depreciation Rate = Original Cost / Number of Years

Depreciation Rate = 6 million / 50 years = $120,000 per year

Years Depreciated = 2014 - 1997 = 17 years

Book Value = 6 million - (120,000 * 17) = 6 million - 2.04 million = $3.96 million

So, the book value of the building in 2014 was $3.96 million.

b) The book value of the building in 2028 can be calculated in a similar manner:

Years Depreciated = 2028 - 1997 = 31 years

Book Value = 6 million - (120,000 * 31) = 6 million - 3.72 million = $2.28 million.

So, the book value of the building in 2028 will be $2.28 million.

To learn more about depreciation click on,

https://brainly.com/question/13202808

#SPJ4

[ (10)(x^3)(y^2) / (5)(x^-3)(y^4) ]^-3

[ (2)(x^3)(y^2) / (x^-3)(y^4) ]^-3

[ (2)(x^6)(y^2) / (y^4) }^-3

[ (2)(x^6)(y^-2) ]^-3

(2^-3)(x^-18)(y^6)

---Not simplified (contains negative exponents)

(1/8)(x^-18)(y^6)

---Fully simplified

(y^6) / (8)(x^18)

Hope this helps!

Answer:

Does the answer help you?

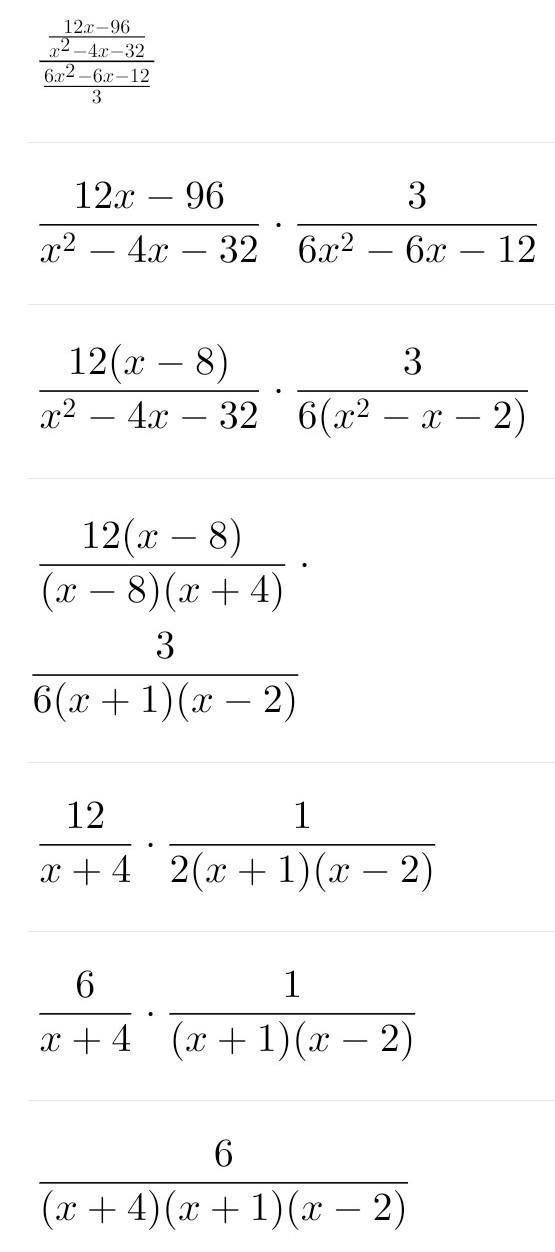
Answer:

6/(x + 4)(x - 2)

Step-by-step explanation:

(12x - 96)/(x² - 4x - 32) ÷ (6x² - 6x - 12)/(3x + 3)

12x - 96 = 12(x - 8)

x² - 4x - 32 = (x - 8)(x + 4)

(12x - 96)/(x² - 4x - 32) = 12/(x + 4)

6x² - 6x - 12 = (3x + 3)(2x - 4)

(6x² - 6x - 12)/(3x + 3) = 2x - 4 = 2(x - 2)

(12x - 96)/(x² - 4x - 32) ÷ (6x² - 6x - 12)/(3x + 3) = 12/(x + 4) ÷ 2(x - 2) = 12/(x + 4) × 1/2(x - 2) = 6/(x+4)(x-2)