How do you upload more than one photo to a question? Also I need help with this problem...

Answers
Answer:
awpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawop
Step-by-step explanation:
awpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawopawpqop24koq2opekwaopkeawop
Related Questions
Take the first 4 digits of your student number as the first number and the last 3 digits as the second number. Write the matlab code to find the greatest common divisor of these numbers using the Euclidean algorithm.
Answers
The required Matlab code to find the greatest common divisor of a number using the Euclidean algorithm is shown.
To find the greatest common divisor (GCD) of two numbers using the Euclidean algorithm in MATLAB, you can use the following code:
% Replace '12345678' with your actual student number
studentNumber = '12345678';
% Extract the first 4 digits as the first number
firstNumber = str2double(studentNumber(1:4));
% Extract the last 3 digits as the second number
secondNumber = str2double(studentNumber(end-2:end));
% Find the GCD using the Euclidean algorithm
gcdValue = gcd(firstNumber, secondNumber);
% Display the result
disp(['The GCD of ' num2str(firstNumber) ' and ' num2str(secondNumber) ' is ' num2str(gcdValue) '.']);
Make sure to replace '12345678' with your actual student number. The code extracts the first 4 digits as the first number and the last 3 digits as the second number using string indexing. Then, the gcd function in MATLAB is used to calculate the GCD of the two numbers. Finally, the result is displayed using the disp function.
Learn more about Matlab code here:
https://brainly.com/question/30763780
#SPJ4
find the area of the shape below 14cm 20cm 9cm 11cm
Answers
Answer:
153 cm²
Step-by-step explanation:
A=21(14+20)×9
A=21×34×9
A=17×9
A=153
given that2025=
\( {3}^{k \times } {5}^{t} \)
state the values of k and t
Answers
Answer:
k = 4, t = 2
Step-by-step explanation:
Express 2025 as a product of its prime factors
2025 = \(3^{4}\) × 5², that is
\(3^{4}\) × 5² = \(3^{k}\) × \(5^{t}\)
Comparing exponents of same bases on both sides, gives
k = 4 and t = 2
The graph of the function f(x)= x^2 − 4x + 6 is shown here. What is its axis of symmetry? A. x = 0 B. x = 2 C. x = 6 D. x = -2

Answers
Answer:
B. x=2
Step-by-step explanation:
If you split it right down the middle and reflect it is exact same.
What is the value of x in trapezoid

Answers
Answer:
Answer: x=15
This is my answer
isosceles trapezoid, the two angles on the legs are the same size, so the other two angles are also equal.
the sum of all the angles is 360°
3x+3x+9x+9x = 360°
24x = 360°
x = 15
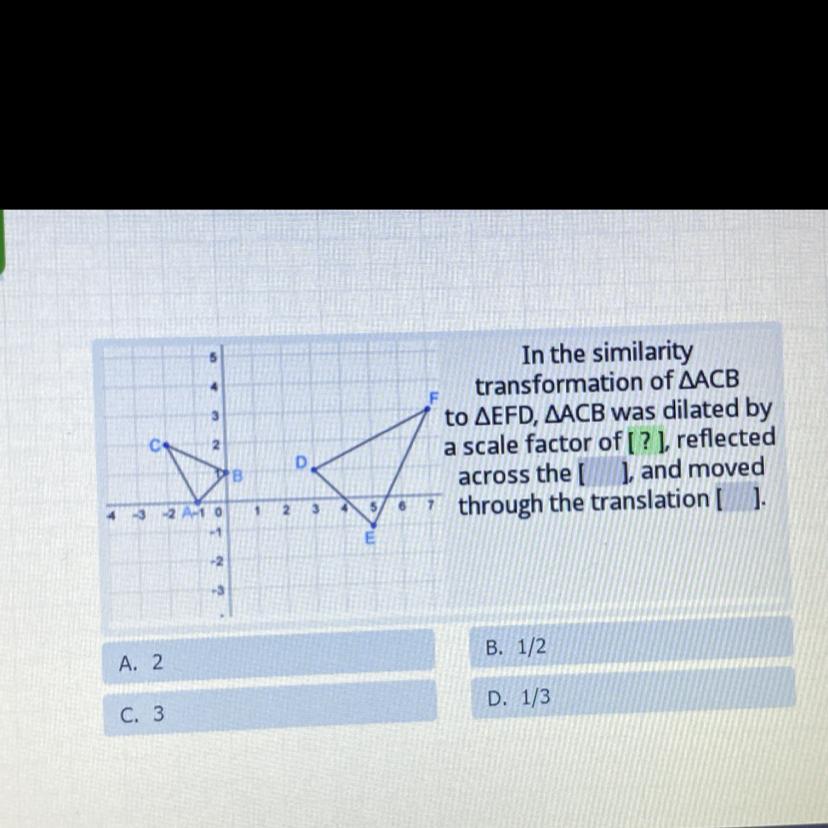
PLEASE HELP IM ON A TIME LIMIT :(
In the similarity
transformation of AACB
to AEFD, AACB was dilated by
a scale factor of [?], reflected
across the [ ], and moved
through the translation[ ].
A. 2
B. 1/2
C. 3
D. 1/3
Answers
Answer:
hey hope this helps
Comparing sides AB and DEAB =
\( \sqrt{ {1}^{2} + {1}^{2} } \)
\( = \sqrt{2} \)
DE
\( = \sqrt{ {(3 - 5)}^{2} + {(1 + 1}^{2} } \\ = \sqrt{ {( - 2)}^{2} + {(2)}^{2} } \\ = \sqrt{4 + 4} \\ = \sqrt{8} \\ = 2 \sqrt{2} \)
So DE = 2 × AB
and since the new triangle formed is similar to the original one, their side ratio will be same for all sides.
scale factor = AB/DE
= 2
It's been reflected across the Y-axis
moved thru the translation of 3 units towards the right of positive x- axis
for this let's compare the location of points B and D
For both the y coordinate is same while the x coordinate of B is 0 and that of D is 3
so the triangle has been shifted by 3 units across the positive x axis
Find a linear inequality with the following solution set. Each grid line represents one unit. [asy] size(200); fill((-2,-5)--(5,-5)--(5,5)--(3,5)--cycle,yellow); real ticklen=3; real tickspace=2; real ticklength=0.1cm; real axisarrowsize=0.14cm; pen axispen=black+1.3bp; real vectorarrowsize=0.2cm; real tickdown=-0.5; real tickdownlength=-0.15inch; real tickdownbase=0.3; real wholetickdown=tickdown; void rr_cartesian_axes(real xleft, real xright, real ybottom, real ytop, real xstep=1, real ystep=1, bool useticks=false, bool complexplane=false, bool usegrid=true) { import graph; real i; if(complexplane) { label("$\textnormal{Re}$",(xright,0),SE); label("$\textnormal{Im}$",(0,ytop),NW); } else { label("$x$",(xright+0.4,-0.5)); label("$y$",(-0.5,ytop+0.2)); } ylimits(ybottom,ytop); xlimits( xleft, xright); real[] TicksArrx,TicksArry; for(i=xleft+xstep; i 0.1) { TicksArrx.push(i); } } for(i=ybottom+ystep; i 0.1) { TicksArry.push(i); } } if(usegrid) { xaxis(BottomTop(extend=false), Ticks("%", TicksArrx ,pTick=gray(0.1),extend=true),p=invisible);//,above=true); yaxis(LeftRight(extend=false),Ticks("%", TicksArry ,pTick=gray(0.1),extend=true), p=invisible);//,Arrows); } if(useticks) { xequals(0, ymin=ybottom, ymax=ytop, p=black, Ticks("%",TicksArry , pTick=black+0.8bp,Size=ticklength), above=true, Arrows(size=axisarrowsize)); yequals(0, xmin=xleft, xmax=xright, p=black, Ticks("%",TicksArrx , pTick=black+0.8bp,Size=ticklength), above=true, Arrows(size=axisarrowsize)); } else { xequals(0, ymin=ybottom, ymax=ytop, p=axispen, above=true, Arrows(size=axisarrowsize)); yequals(0, xmin=xleft, xmax=xright, p=axispen, above=true, Arrows(size=axisarrowsize)); } }; draw((-2,-5)--(3,5),dashed+red, Arrows(size=axisarrowsize)); rr_cartesian_axes(-5,5,-5,5); f
Answers
The linear inequality of the graph is: -x + 2y + 1 > 0
How to determine the linear inequality?First, we calculate the slope of the dashed line using:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
Two points on the graph are:
(1, 0) and (3, 1)
The slope (m) is:
\(m = \frac{1 - 0}{3 - 1}\)
This gives
m = 0.5
The equation of the line is calculated as:
\(y = m(x -x_1) + y_1\)
So, we have;
\(y = 0.5(x -1) + 0\)
This gives
\(y = 0.5x -0.5\)
Multiply through by 2
\(2y = x - 1\)
Now, we convert the equation to an inequality.
The line on the graph is a dashed line. This means that the inequality is either > or <.
Also, the upper region of the graph that is shaded means that the inequality is >.
So, the equation becomes
2y > x - 1
Rewrite as:
-x + 2y + 1 > 0
So, the linear inequality is: -x + 2y + 1 > 0
Learn more about linear inequality at:
brainly.com/question/19491153
#SPJ1
Complete question
Find a linear inequality with the following solution set. Each grid line represents one unit. (Give your answer in the form ax+by+c>0 or ax+by+c \(\geq\) 0 where a, b, and c are integers with no common factor greater than 1.)
![Find a linear inequality with the following solution set. Each grid line represents one unit. [asy] size(200);](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/UjoLffnXWYGqb3UWZR2cPzUa8iui54PG.jpeg)
In triangle QPC a unique triangle or can more than one triangle be formed using the three angle measures? Justify your answer.

Answers
The answer is yes, more than one triangle can be formed using the three angle measures of triangle QPC. This is because the sum of the three angle measures of a triangle is always equal to 180 degrees.
What is a triangle?A triangle is a three-sided geometric figure, consisting of three straight lines connecting three vertices. It is one of the most fundamental shapes in geometry and is used as the basis for a variety of mathematical concepts.
If two angle measures are given, any third angle measure between 0 and 180 degrees can be chosen to form a triangle. Thus, if two angle measures of triangle QPC are given, any third angle measure between 0 and 180 degrees can be used to form a triangle.
For example, if two angle measures of triangle QPC are 45 degrees and 65 degrees, then any third angle measure between 0 and 180 degrees can be chosen to form a triangle. Thus, if the third angle measure chosen is 70 degrees, then a triangle with three angle measures of 45 degrees, 65 degrees and 70 degrees can be formed. Similarly, if the third angle measure chosen is 30 degrees, then a triangle with three angle measures of 45 degrees, 65 degrees and 30 degrees can be formed.
Thus, it can be concluded that more than one triangle can be formed using the three angle measures of triangle QPC.
For more questions related to geometric,
https://brainly.com/question/11266123
#SPJ1
a store employees 11 women and 12 men.what percentage of employees are men?
Answers
Answer:
easy just find the total of how many people work there then put that no. as a denominator and put 12 on the numerator then times it by 100 and the answer should be 52.2% or 52.17%
Answer:
52.2% or 52.17%
12 men
Total = 23
12 / 23 =
A shirt is on sale 60% of the Original price.The oiginal price is $28 more then the sale price.What was the original price
Answers
Step-by-step explanation:
To solve for this problem you can write and equation with × being the original price:
6x + 28 = X
Solving for x you you can get:
28 = 4x
× = 70
Triangle A has a single transformation performed on it to create Triangle B. Michelle says the single transformation must have been a translation 8 units to the right.
what is the transformation that could have been performed on Triangle A to create Triangle B to prove Michelle's statement is false.
Answers
Answer:The single transformation that maps triangle A onto triangle B is the reflection about the x-axis
Step-by-step explanation:
what does "10000" in binary notation represent in ordinary (decimal) numbers?
Answers
In binary notation, the number "10000" represents the value of 16 in ordinary (decimal) numbers. Binary notation is a numbering system that uses only two digits, 0 and 1, to represent all numbers.
Each digit in a binary number represents a power of two, with the rightmost digit representing 2^0, the second-rightmost digit representing 2^1, and so on. In the number "10000", the leftmost digit represents 2^4, or 16, while all other digits are 0.
Therefore, the binary number "10000" is equal to the decimal number 16. It is important to note that binary notation is commonly used in computer programming and digital electronics, while ordinary (decimal) numbers are used in everyday life and most other fields of study.
To know more about binary notation visit:
https://brainly.com/question/14811568
#SPJ11
Which of these would be a helpful first step in solving the equation? Check all that apply.
9x + 5 = 5x + 21
A. subtract 5x
B. divide by 3
C. subtract 16
D. divide by 9
E. subtract 5
Answers
I believe it would be A and E. Good luck!!:)
Can anyone help me plos?
how many pounds of $2.4/lb trail mix should a grocer combine with 5 lb of 1.5/lb trail mix to get $1.9/lb trail mix?
Answers
That the grocer should combine 7 pounds of $2.4/lb trail mix with 5 pounds of $1.5/lb trail mix to get $1.9/lb trail mix.
we can use a weighted average formula to solve for the amount of $2.4/lb trail mix needed. We can represent the amount of $2.4/lb trail mix as x, and set up the equation:
(2.4x + 1.5(5)) / (x + 5) = 1.9
Simplifying the equation, we get:
2.4x + 7.5 = 1.9x + 9.5
0.5x = 2
x = 4
Therefore, we need to combine 7 pounds of trail mix ($2.4/lb) with 5 pounds of trail mix ($1.5/lb) to get 12 pounds of trail mix at $1.9/lb.
by using the weighted average formula, we can determine the amount of each type of trail mix needed to achieve the desired price per pound. In this case, combining 7 pounds of $2.4/lb trail mix with 5 pounds of $1.5/lb trail mix will result in a 12 pound mixture at $1.9/lb.
To know more about pounds visit:
https://brainly.com/question/29181271
#SPJ11
Find the arc length of the graph of the function over the indicated interval. x= 1/3 (y^2+2)^3/2 0≤y≤7
Answers
The arc length of the graph of the function x = 1/3(y^2 + 2)^(3/2) over the interval 0 ≤ y ≤ 7 is approximately 94.81 units.
To find the arc length, we can use the formula for arc length of a curve given by the integral of √(1 + (dx/dy)^2) dy. In this case, the derivative of x with respect to y is (1/3)(y^2 + 2)^(1/2)(2y), which simplifies to (2/3)y(y^2 + 2)^(1/2).
Substituting this into the formula, we have:
∫[0,7] √[1 + ((2/3)y(y^2 + 2)^(1/2))^2] dy.
Simplifying the expression inside the square root and integrating, we find the arc length to be approximately 94.81 units.
To find the arc length of the graph of a function over a given interval, we use the formula for arc length: L = ∫[a,b] √[1 + (dx/dy)^2] dy, where a and b represent the limits of the interval and dx/dy is the derivative of x with respect to y.
In this case, we are given the function x = 1/3(y^2 + 2)^(3/2) and the interval 0 ≤ y ≤ 7. To compute the derivative dx/dy, we apply the chain rule. Taking the derivative of the outer function, we get (3/2)(y^2 + 2)^(1/2)(2y) and multiplying it by the derivative of the inner function, which is 1. Simplifying further, we obtain (2/3)y(y^2 + 2)^(1/2).
Substituting the derivative into the arc length formula, we have L = ∫[0,7] √[1 + ((2/3)y(y^2 + 2)^(1/2))^2] dy. Now, we need to simplify the expression inside the square root before integrating. Squaring the derivative and adding 1 gives us 1 + (4/9)y^2(y^2 + 2). Simplifying this further, we have 1 + (4/9)(y^4 + 2y^2).
Taking the square root of this expression and integrating with respect to y over the given interval, we find the arc length to be approximately 94.81 units.
Learn more about graph here:
brainly.com/question/17267403
#SPJ11
Find the critical value Za /2 that corresponds to 98% confidence level A. 2.575 B. 2.05 C. 1.75 D. 2.33
Answers
Answer:
The critical value Za /2 that corresponds to 98% confidence level is (d) 2.33
Step-by-step explanation:
To obtain the critical value Za/2 that corresponds to a 98% confidence level, we need to determine the value that leaves 2% (0.02) in the tails of the distribution.
Since the confidence level is two-tailed, we need to divide the significance level by 2 to find the area in each tail. In this case, we have 2% divided by 2, resulting in 1% (0.01) in each tail.
Looking up the critical value in a standard normal distribution table or using statistical software, we obtain that the closest value to 0.01 in the table is approximately 2.33.
Therefore, the correct answer is D. 2.33.
Learn more about confidence level here, https://brainly.com/question/15712887
#SPJ11
A food cooperative is a business that usually offers special prices on locally grown food and produce. Some are clubs and some are retail stores. A club costs a one time club fee of $20 and a cost of $15 per week. A retail store costs no club fee and a cost of $17.50 per week. After how many weeks will the cost of the club and the retail be the same?
Answers
Answer:
The indifference point is 8 weeks.
Step-by-step explanation:
First, we establish the total cost formula for each:
x= number of weeks
Club:
Total cost= 20 + 15*x
Retail:
Total cost= 17.5*x
Now, we equal both formulas and isolate x:
20 + 15x = 17.5x
20 = 2.5x
8=x
The indifference point is 8 weeks.
Prove:
Total cost= 20 + 15*8= $140
Total cost= 17.5*8= $140
observations 1 2 3 4 5 6 num. of defects 10 18 13 15 9 12the number of runs above and below the sample median is:
Answers
The median element of a dataset is the middle element of the dataset.
There are 3 runs above and below the sample median
What is the median of a data set ?
The median of a data set is the value that falls in the middle, indicating that 50% of the data points have values that are lower or equal to the median and 50% of the data points have values that are higher or equal to the median. When working with a small data collection, you must first count the number of data points (n) and organize them in ascending order.
The information is given as:
Observations 1 2 3 4 5 6
Defects 10 18 13 15 9 12
In ascending order, the information is represented as:
Defects 9 10 12 13 15 18
Observations 5 1 6 3 4 2
The total number of observations is:
n=5+1+6+3+4+2 = 21
The median element is calculated as:
Median = (n+1)/2 th
Substitute 21 for n
Median = (21+1)/2 th
Median = 11th
The 11th element is 12.
So, the median is:
median = 12
Considering the given information;
Observations 1 2 3 4 5 6
Defects 10 18 13 15 9 12
The defects greater than the median (i.e. 12) are above (A) the median, while the defects less than the median are below (B)
So, we have:
Observations 1 2 3 4 5 6
Defects 10 18 13 15 9 12
Status B A A A B -
Next, we take a count of the number of times the status changes, i.e. from B to A, from A to B, from A or B to -
The count is 3.
Hence, there are 3 runs above and below the sample median
To learn more about median at:
brainly.com/question/6587502
#SPJ4
Please help. I thought I worked it out correctly but the answer is apparently wrong

Answers
Answer:
ready-steady paint
Step-by-step explanation:
if he needs 12 tins, and purchased from paint -O mine, he would spend (12/3) X 7.50 = 4 x 7.50 = £30
from ready steady, he can buy 4 for £11. he needs 12.
so he will spend (12/4) X 11 = 3 X 11 = £33. but he can get 15% off. 15% off is the same as multiplying by 0.85.
33 X 0.85 = £28.05.
so he his better purchasing from ready steady paint
Find the general solution of the following differential equation. Primes denote derivatives with respect to x. 3x^2y' +6xy = 15y^3 The general solution is ___
Answers
The general solution of the differential equation is \(& y=\sqrt{\frac{x}{2+c x^5}}\).
The general solution of the following differential equation is \($\quad 3 x^2 y^{\prime}+6 x y=15 y^3$\).
When the arbitrary constant of the general solution takes some unique value, then the solution becomes the particular solution of the equation.The differential equations which are represented in terms of (x,y) such as the x-terms and y-terms can be ordered to different sides of the equation (including delta terms). Thus, each variable after separation can be integrated easily to find the solution of the differential equation. The equations can be written as:
\(f(x) dx+g(y)dy=0\), where f(x) and g(y) are either constants or functions of x and y respectively.solution: \($\quad y^{\prime}=\frac{d y}{d x}$\)
So rewritten question as
\($$\begin{aligned}& 3 x^2 \frac{d y}{d x}+6 x y=15 y^3 \\& \frac{d y}{d x}+\frac{6 x y}{3 x^2}=\frac{15 y^3}{3 x^2} \\& \frac{d y}{d x}+\frac{2 y}{x}=\frac{5}{x^2} y^3\end{aligned}$$\)
compare equation (1) with Bernoulli's Equation
\($$\begin{aligned}& \frac{d y}{d x}+P(x) y=Q(x) y^n \\& P(x)=\frac{2}{x} \quad Q(x)=\frac{5}{x^2} \\& n=3\end{aligned}$$\)
Substitute:
\(v & =y^{1-n} \\v & =y^{1-3} \\v & =y^{-2} \\y \quad y & =v^{(-1 / 2)}-(2) \\\frac{d y}{d x} & =-\frac{1}{2}\left(v^{-\frac{1}{2}-1}\right) \frac{d v}{d x}\end{aligned}$$\)
\(\frac{d y}{d x}=-\frac{1}{2} v^{-3 / 2} \frac{d v}{d x}\)
substitute value of y and \($\frac{d y}{d x}$\) from 4 (2) and (3) respectively in equation (1)
⇒\(& \frac{-1}{2} v^{-3 / 2} \frac{d v}{d x}+\frac{2}{x} \cdot v^{-1 / 2}=\frac{5}{x^2} \cdot v^{-3 / 2}\)
⇒\(& \frac{d v}{d x}-\frac{4}{x} v=\frac{-10}{x^2} \\\)
⇒ Integrating factor\(=e^{\int-4 / x d x} \\\)
\(& =e^{-4 \ln x} \\& =e^{\ln x^{-4}} \\& =x^{-4} \\& =\frac{1}{x^4} \\\)
⇒\(\frac{1}{x^4} v=\int \frac{1}{x^4} \times \frac{-10}{x^2} d x \\\)
\(& =-10 \int x^{-6} d x \\\)
\(& =+10 \frac{x^{-6+1}}{(-6+1)}+C=\frac{+10^2}{+8} x^{-5}+C \\&\)
⇒\(\frac{1}{x^4} \cdot v & =\frac{2}{x^5}+c \\\)
⇒\(v & =\left(\frac{2}{x^5}+c\right) x^4 \\\)
⇒\(v & =\left(\frac{2}{x}+c x^4\right)\)
Now replace v=y-2
⇒\(& y^{-2}=\frac{2}{x}+c x^4 \\\)
⇒\(& y=\left[\frac{1}{\left(\frac{2}{x}+\left(x^4\right)\right.}\right]^{1 / 2} \\\)
⇒\(& y=\sqrt{\frac{x}{2+c x^5}}\)
Therefore, the general solution of the differential equation is \(& y=\sqrt{\frac{x}{2+c x^5}}\).
For more such questions on Bernoulli's Equation
https://brainly.com/question/21852102
#SPJ4
find the missing side

Answers
Answer:
\(\boxed{x=13.89\:km}\)
Step-by-step explanation:
Pythagorean theorem
\(x^2=(12^2)+(7^2)\)
\(x^2=144+49\)
\(x^2=193\)
\(x=\sqrt{193}\)
\(\boxed{x=13.89\:km}\)
i need help fast with this problem

Answers
Answer:
6 is the answer
Step-by-step explanation:
Help please can you help me

Answers
The required equation of the circle is (x - 2)² + (y + 3)² = 10².
The standard form of the equation of a circle with center (h, k) and radius r is:
(x - h)² + (y - k)² = r²
Given that the center of the circle is (2, -3), so h = 2 and k = -3.
To find the radius r, we can use the distance formula between the center and the point on the circle:
r = sqrt((x - h)² + (y - k)²)
We are also given that point (8, 5) is on the circle.
Substituting the values of h, k, x, and y into the distance formula, we have:
r = √((8 - 2)² + (5 - (-3))²)
r = √(6² + 8²)
r = 10
Therefore, the equation of the circle in (x-h)² + ( y −k)² = r² form is:
(x - 2)² + (y + 3)² = 10²
Learn more about the equation of a circle here:
brainly.com/question/1554214
#SPJ1
Matthew has a standard deck of cards. There are four suits with 13 cards in each from ace through to king. He shuffles the deck and selects one card and then another. In its simplest form, what is the probability that he draws a pair of tens? 1st attempt: probability of getting a pair of 10s.
Answers
The probability that he draws a pair of tens is 1/2652 or approximately 0.000378 which is approx 0.04%
The probability of drawing a pair of tens from a standard deck of cards is (number of ways to get a pair of tens) / (total number of possible outcomes).
In this case there are 4 tens (2 of hearts, 2 of diamonds, 2 of spades, 2 of clubs) and he is drawing 2 cards from the deck, so there is only 1 way to get a pair of tens. There are 52 cards in a standard deck, so the total number of possible outcomes is 52 * 51 = 2652.
So the probability of drawing a pair of tens is 1/2652 or approximately 0.000378 which is approx 0.04%
Learn more about probability here: https://brainly.com/question/24756209
#SPJ4
all you need is in the photo PLEASE DON'T DO STEP BY STEP BECAUSE IS SO CONFUSING PUT ONLY THE ANSWER

Answers
A) The ball in the ground is represented by h(t)=0, that is, the height is equal to 0, the reference level.
Then, we can find for which values of t we have h(t).
We equal h(t) to 0 and calculate t as:
\(\begin{gathered} h(t)=-16t^2+64t=0 \\ 64t-16t^2=0 \\ 16t(\frac{64}{16}-t)=0 \\ t_1=0\text{ (first solution)} \\ t_2=\frac{64}{16}=4\text{ (second solution)} \end{gathered}\)The ball is in the ground at time t=0 (an instant before it is kicked) and then again at time t=4, that is the value we are looking for: the ball landed again in the ground 4 seconds after kicked.
B) The maximum height can be find in two ways:
- By finding the t-value of the vertex, that in this case will be correspond to the maximum height as this is a concave down parabola with only one extreme point.
- Deriving the function and equaling to 0 and finding t.
If we apply the first method, we have:
\(\begin{gathered} h(t)=-16t^2+64x=-16(x^2-4x) \\ -16(x^2-4x) \\ -16(x^2-4x+4-4) \\ -16((x-2)^2-4) \\ -16(x-2)^2+64\longrightarrow\text{Vertex:}(2,64) \end{gathered}\)As the vertex is at time t=2 seconds, the maximum height happens at t=2.
Answer: A) t = 4 seconds B) t = 2 seconds
NOTE for Part B:
If we derive the expression, we get:
\(undefined\)find the value of X, y and z
ans: x=50 y= 50 z=50

Answers
The value of x , y and z in the parallel line is 50 degrees.
How to find the angle in parallel line?When parallel lines are crossed by a transversal line, angle relationships are formed such as vertically opposite angles, alternate interior angles, alternate exterior angles, adjacent angles, corresponding angles etc.
Therefore, let's use the angle relationships to find the angle, x, y and z as follows:
Therefore,
x = 360 - 310(sum of angles in a point)
x = 50 degrees
Therefore,
x = y(alternate interior angles)
Alternate interior angles are congruent.
Hence,
y = 50 degrees
Therefore,
x = z(alternate interior angles)
z = 50 degrees.
learn more on angles here: https://brainly.com/question/17043791
#SPJ1
please help me i don’t understand

Answers
9514 1404 393
Answer:
2. chord theorem; t = 10.5
3. chord theorem; x = 5
Step-by-step explanation:
For both of these problems, the relevant theorem is the "intersecting chord theorem", also referred to as the "chord theorem." It tells you the product of the lengths of the parts of one chord is equal to the product of the lengths of the parts of the other chord.
2. 20t = 10·21
t = 210/20 . . . . divide by 20
t = 10.5 . . . . . . . simplify
__
3. 10(x +4) = 15(x +1)
10x +40 = 15x +15 . . . . . eliminate parentheses
25 = 5x . . . . . . . . . . . . . subtract 10x+15
5 = x . . . . . . . divide by 5
Choose the fraction that has not been reduced to simplest form.

Answers
Answer:
19/38 can be simplified to 1/2
Step-by-step explanation:
What is the measure of an angle that is the complement of angle K?

Answers
Answer:
Sum of complementary angles is 90
90-25=65°
Step-by-step explanation:
based on derivative how many times can function cross the x-asix
Answers
Based on the derivative, a function can cross the x-axis a certain number of times depending on the number of times the derivative changes sign.
A derivative is a mathematical tool that measures the rate of change of a function at a specific point. Specifically, it is the slope of the tangent line to the function at that point. The derivative can be used to determine where a function is increasing, decreasing, or reaching a maximum or minimum value.
When a function crosses the x-axis, it means that the y-value of the function is equal to zero. In order for a function to cross the x-axis, it must change sign from positive to negative or vice versa. This happens when the function passes through a maximum or minimum point.
If the derivative of the function is positive at a point, it means that the function is increasing at that point. If the derivative is negative, the function is decreasing. If the derivative is zero, it means that the function is neither increasing nor decreasing, and it could be at a maximum or minimum point.
Therefore, the number of times a function can cross the x-axis depends on the number of times the derivative changes sign. If the derivative changes sign twice, the function can cross the x-axis twice. However, if the derivative changes sign an odd number of times, the function can only cross the x-axis once.
Learn more about derivative here:
https://brainly.com/question/29144258
#SPJ11