How do you find the square root of -6 by imaginary numbers
Answers
To find the square root of a negative number use the next:
\(\sqrt{-1}=i\)For -6:
You can write -6 as the product of 6 and -1:
\(\sqrt{\left(6\right)*\left(-1\right)}\)The square root of a product is the same as the product of the square root if each of the factors:
\(=\sqrt{6}*\sqrt{-1}\)As the square root of 6 is not a exact number (it has many decimals) you leave the square root of 6 as it is. The square root of -1 is i; then, the square root of -6 is:
\(\begin{gathered} =\sqrt{6}*i \\ =\sqrt{6}i \end{gathered}\)Then, the square root of -6 is: (√6)iRelated Questions
PLEASE HELP DUE SOON! PLEASE SHOW WORK SO I KNOW HOW TO IT FOR NEXT TIME! IM STUCK ON THIS AND ITS DUE TODAY!!!!! YOU WILL GETT 100 POINTS REAL ANSWERS ONLY! MANY THANKS! QUESTIONS DOWN BELOW!!!!!

Answers
Answer:
a) zero triangles.
b) one triangle.
Step-by-step explanation:
In triangle ABC:
A, B and C are the interior angles.a, b and c are the sides opposite the corresponding interior angles.Part (a)Given:
∠A = 51°a = 10 cmb = 28 cmLaw of Sines
\(\sf \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\)
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
To determine if any triangles are possible, substitute the given values into the Law of Sines to find angle B:
\(\implies \sf \dfrac{\sin 51^{\circ}}{10}=\dfrac{\sin B}{28}\)
\(\implies \sf \sin B=\dfrac{28\sin 51^{\circ}}{10}\)
\(\implies \sf \sin B=2.176008...\)
As -1 ≤ sin B ≤ 1, there is no solution for angle B.
Therefore, zero triangles are possible.
----------------------------------------------------------------------------------
Part (b)Given:
∠C = 30°a = 24 cmc = 12 cmLaw of Sines
\(\sf \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\)
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
To determine if any triangles are possible, substitute the given values into the Law of Sines to find angle A:
\(\implies \sf \dfrac{\sin A}{24}=\dfrac{\sin 30^{\circ}}{12}\)
\(\implies \sf \sin A=\dfrac{24\sin 30^{\circ}}{12}\)
\(\implies \sf \sin A=1\)
\(\implies \sf A=\sin^{-1}(1)\)
\(\implies \sf A=90^{\circ}\)
Therefore, one triangle is possible (see attachment).

The table represents a linear relationship
X—2 0 4
Y-4 3 1
Which equation represents the table
Y=1/2x+5
y=-1/2x+3
Y=2x-3
Y=-4x+2
Answers
The linear relationship illustrated in the provided table can be effectively described by the equation Y = -4x + 2. Option D.
To determine the equation that represents the given table with the values of x and y, we can observe the pattern and find the equation of the line that fits these points.
Given the table:
X: 2 0 4
Y: -4 3 1
We can plot these points on a graph and see that they form a straight line.
Plotting the points (2, -4), (0, 3), and (4, 1), we can see that they lie on a line that has a negative slope.
Based on the given options, we can now evaluate each equation to see which one represents the line:
Y = 1/2x + 5
When we substitute the x-values from the table into this equation, we get the following corresponding y-values: -3, 5, and 6. These values do not match the given table, so this equation does not represent the table.
Y = -1/2x + 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: 4, 3, and 2. These values also do not match the given table, so this equation does not represent the table.
Y = 2x - 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -4, -3, and 5. These values do not match the given table, so this equation does not represent the table.
Y = -4x + 2
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -6, 2, and -14. Interestingly, these values match the y-values in the given table. Therefore, the equation Y = -4x + 2 represents the table.
In conclusion, the equation Y = -4x + 2 represents the linear relationship described by the given table. So Option D is correct.
For more question on equation visit:
https://brainly.com/question/29174899
#SPJ8
How does the calculator get 48.8? mean (45, 80, 15, 10, 94)
Answers
Answer:
mean= sum of all observations /no.of observation
mean=45+80+15+10+94/5
mean=244/5
mean=48.8
this is how the calculator gets 48.8
True or false
-y = -112 + 4; (0, -4)
Answers
Answer:
False
Step-by-step explanation:
The coordinates of points A and B are A (15, 20) and B (31,52). Which are the
coordinates of a point that partitions segment AB in a ratio of 1:3?
PHOTO HERE

Answers
Answer:
(19, 28)
Step-by-step explanation:
B. What is each piece measurement if the angle is cut into 9 equal
lengths? Kerf width is 0.125.

Answers
Each piece Measurement of an angle of 120 degrees cut into nine equal lengths with a kerf width of 0.125 would be 14.4583 degrees.
When a particular angle is cut into nine equal parts, the measure of each piece needs to be calculated.
Therefore, it is essential to first calculate the total angle measure and then divide it by the number of parts into which it is being cut.
What is an Angle?
An angle is a geometrical shape that consists of two rays sharing a common endpoint. The common endpoint is known as the vertex, and the two rays are known as the arms of the angle. An angle can be measured in degrees, radians, or gradians. Degrees are the most commonly used unit of measuring angles.How to Calculate Each Piece Measurement of an Angle if Cut into 9 Equal Lengths
To determine each piece measurement of an angle if cut into nine equal lengths, we will need to carry out the following steps:
Step 1: Calculate the total angle measure Suppose the angle being cut into nine equal lengths is an obtuse angle measuring 120 degrees. In that case, the total angle measure will be 120 degrees.
Step 2: Divide the total angle measure by the number of parts into which it is being cut.120 degrees ÷ 9 = 13.3333 degrees
Step 3: Add the kerf width to the piece measurements.0.125 x 9 = 1.125 degrees13.3333 + 1.125 = 14.4583 degrees
Therefore, each piece measurement of an angle of 120 degrees cut into nine equal lengths with a kerf width of 0.125 would be 14.4583 degrees.
For more questions on Measurement .
https://brainly.com/question/27233632
#SPJ8
If you are buying at item at a store for a price of $77, and there is a 7.5% tax added on
top, what would be the total amount due at the register, to the nearest cent?
Answers
Answer:
82.76
Step-by-step explanation:
77 x 7.5%=5.775
5.775 +77
Similar triangles: To indirectly measure the distance across a river, Madeline stands on one side of the river and uses sight-lines to a landmark on the opposite bank. Madeline draws the diagram below to show the lengths and angles that she measured. Find PR, the distance across the river. Round your answer to the nearest foot.

Answers
Answer:
PR = 288.75 feet
Step-by-step explanation:
There are two triangles that we need to consider:
ΔPRE and ΔPOC
These triangles are similar since
m∠PRE = m∠POC = 90°
∠PRE ≅ ∠POC
∠RPE ≅ ∠OPC (common angle)
AA Similarity theorem..
If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
∴ ΔPRE ≅ ΔPOC
If two triangles are similar, the ratios of the corresponding sides must be equal
⇒ \(\dfrac{PO}{PR} = \dfrac{OC}{PE}\\\\\) (1)
PO = PR + RO
PR is the width of the river that is to be determined
Let PR = x
Then
PO = x + 165
OC = 330, RE = 210
\(\dfrac{PO}{PR} = \dfrac{OC}{PE}\\\\\Rightarrow \dfrac{x + 165}{165} = \dfrac{330}{210}\\\\\)
Left side:
\(\dfrac{x+165}{x} = \dfrac{x}{x} + \dfrac{165}{x} = 1 + \dfrac{165}{x}\)
Simplify \(\dfrac{330}{210}\) by dividing both numerator and denominator by 30
=>
\(\dfrac{330}{210} = \dfrac{11}{7}\\\\\)
Therefore
\(\dfrac{PO}{PR} = \dfrac{OC}{PE}\\\\\Rightarrow 1 + \dfrac{165}{x} = \dfrac{11}{7}\\\)
Subtract 1 from both sides:
\(\dfrac{165}{x} = \dfrac{11}{7} - 1\\\\\dfrac{165}{x} = \dfrac{4}{7}\\\\\)
Cross-multiply
\(165 \times 7 = 4x\\\\\Rightarrow 4x = 165 \times 7\\\\\Rightarrow x = \dfrac{165 \times 7 }{4} = 288.75\;feet\)
Question Help
A local little league has a total of 70 players, of whom 80% are right-handed. How many
right-handed players are there
Answers
Answer:
The number of right-handed people = 56
Step-by-step explanation:
80% of 70 players = number of right-handed people
So, 80/100 x 70 = 56 players
Therefore, number of right-handed players = 56
Oil is pumped continuously from a well at a rate proportional to the amount of oil left in the well. Initially there were million barrels of oil in the well; six years later barrels remain.At what rate was the amount of oil in the well decreasing when there were barrels remaining
Answers
Answer:
The amount of oil was decreasing at 69300 barrels, yearly
Step-by-step explanation:
Given
\(Initial =1\ million\)
\(6\ years\ later = 500,000\)
Required
At what rate did oil decrease when 600000 barrels remain
To do this, we make use of the following notations
t = Time
A = Amount left in the well
So:
\(\frac{dA}{dt} = kA\)
Where k represents the constant of proportionality
\(\frac{dA}{dt} = kA\)
Multiply both sides by dt/A
\(\frac{dA}{dt} * \frac{dt}{A} = kA * \frac{dt}{A}\)
\(\frac{dA}{A} = k\ dt\)
Integrate both sides
\(\int\ {\frac{dA}{A} = \int\ {k\ dt}\)
\(ln\ A = kt + lnC\)
Make A, the subject
\(A = Ce^{kt}\)
\(t = 0\ when\ A =1\ million\) i.e. At initial
So, we have:
\(A = Ce^{kt}\)
\(1000000 = Ce^{k*0}\)
\(1000000 = Ce^{0}\)
\(1000000 = C*1\)
\(1000000 = C\)
\(C =1000000\)
Substitute \(C =1000000\) in \(A = Ce^{kt}\)
\(A = 1000000e^{kt}\)
To solve for k;
\(6\ years\ later = 500,000\)
i.e.
\(t = 6\ A = 500000\)
So:
\(500000= 1000000e^{k*6}\)
Divide both sides by 1000000
\(0.5= e^{k*6}\)
Take natural logarithm (ln) of both sides
\(ln(0.5) = ln(e^{k*6})\)
\(ln(0.5) = k*6\)
Solve for k
\(k = \frac{ln(0.5)}{6}\)
\(k = \frac{-0.693}{6}\)
\(k = -0.1155\)
Recall that:
\(\frac{dA}{dt} = kA\)
Where
\(\frac{dA}{dt}\) = Rate
So, when
\(A = 600000\)
The rate is:
\(\frac{dA}{dt} = -0.1155 * 600000\)
\(\frac{dA}{dt} = -69300\)
Hence, the amount of oil was decreasing at 69300 barrels, yearly
1)
Science 5
Measurement Assignment
Name each measurement instrument below. Then, indicate which
type of measurement is performed with each one. Remember,
some instruments can be used for more than one type of
measurement!
Instrument
Name of Instrument
Measurement Type

Answers
Answer: See below
Step-by-step explanation:
The first is a beaker, it's used to measure liquid volume
The second is a ruler, it's used to measure length.
Last is a thermometer, it's used to measure temperature.
A tip employee’s earnings most closely resemble those of which of the following?
a.
An employee working on straight commission
b.
An employee working on commission plus salary
c.
An employee working on a piece-rate basis
d.
An employee working on a fixed salary
Answers
Answer:
It's b, a waiter does get paid a paycheck but it isn't much, tips also count as commission. Tip your waiters!
Step-by-step explanation:
Also brainly says the word "b r u h" is inappropriate what terrible moderation on this site.
Which of the following is an example of a continuous random variable?a. A Bernoulli trial
b. Binomial random variable
c. Normal random variable
d. Discrete uniform random variable
Answers
An example of a continuous random variable is a Normal random variable.
What is a normal random variable?
A random variable is a variable with an unknown value or a function that gives values to each of the results of an experiment. A random variable can be either discrete (having definite values) or continuous (any value in a continuous range).
Here, we have
We have to determine the example of a continuous random variable.
We concluded that the example of a continuous random variable is a normal random variable.
Hence, an example of a continuous random variable is a Normal random variable.
To learn more about the normal random variable from the given link
https://brainly.com/question/4079902
#SPJ1
Roy has three yellow counters and five red counters. How
many counters does he have in all? I.
Answers
Answer:
he has 8 counters.
Step-by-step explanation:
3+5=8
Answer:
8
Step-by-step explanation:
5+3= 8
Need help on finding g .

Answers
The numeric values for this problem are given as follows:
g(-1) = -2.g(2) = 0.g(3) = 0.5.How to obtain the numeric values of the function?The function in this problem is a piecewise function, meaning that it has different definitions based on the input x of the function.
For x between -2 and 2, the function is defined as follows:
g(x) = -(x - 1)² + 2.
Hence the numeric value at x = -1 is given as follows:
g(-1) = -(-1 - 1)² + 2 = -4 + 2 = -2.
For x at x = 2 and greater, the function is given as follows:
g(x) = 0.5x - 1.
Hence the numeric values at x = 2 and x = 3 are given as follows:
g(2) = 0.5(2) - 1 = 0.g(3) = 0.5(3) - 1 = 0.5.A similar problem, also featuring numeric values of a function, is given at brainly.com/question/28367050
#SPJ1
Find the inverse of the function using complete sentence

Answers
There are 9 apples in each
Box. How many Apples are in
in 6 boxes
Answers
Answer:
I believe h do 9 times 6. and u should get 54
A large university offers STEM (science, technology,engineenng. And mathematics) intemshups to women in STEM majors at the university. A woman must be 20 years or older to meet the age requirement for the intemships. The table shows the probability distribution of the ages of the women in STEM majors at the university Age (years) 17 18 19 20 21 22 23 or older Probability 0. 063 0. 005 0. 107 0. 111 0. 252 0. 249 0. 213 (a) Suppose one woman is selected at random from the women in STEM majors at the university. What is the probahility that the woman selected will not meet the age requirement for the internships?(b) Suppose a simple random sampling process is used to select the sample of 100 women. What is theprobability that at least 30 percent of the women in the sample will not meet the age requirement for the internships?
Answers
a) The probability that the woman selected will not meet the age requirement for the internships is:
0.175
b) The probability that at least 30% of the women in the sample will not meet the age requirement for the internships is:
0.0003
a) What is the probahility that the woman selected will not meet the age requirement for the internships?The probability that a woman selected at random from the women in STEM majors at the university will not meet the age requirement for the internships can be found by adding the probabilities of the ages that do not meet the age requirement. This includes the probabilities for ages 17, 18, and 19, which are 0.063, 0.005, and 0.107, respectively. Adding these probabilities gives us:
P(not meeting age requirement) = 0.063 + 0.005 + 0.107 = 0.175
This can be found using the binomial probability formula:
P(X ≥ 30) = 1 - P(X < 30) = 1 - ∑(n choose x) * p^x * (1-p)^(n-x)
Where n is the sample size (100), x is the number of women not meeting the age requirement (less than 30), and p is the probability of not meeting the age requirement (0.175). Using this formula, we can find the probability that at least 30% of the women in the sample will not meet the age requirement for the internships:
P(X ≥ 30) = 1 - P(X < 30) = 1 - ∑(100 choose x) * 0.175^x * (1-0.175)^(100-x)
P(X ≥ 30) = 1 - (0.825^100 + (100 choose 1) * 0.175 * 0.825^99 + ... + (100 choose 29) * 0.175^29 * 0.825^71)
P(X ≥ 30) = 0.0003
More information about the probability here: https://brainly.com/question/11455301
#SPJ11
SLOPE DIGITAL ESCAPE ROOM
I need help finding the code

Answers
By finding all the four slopes, we can see that the word is ECHA.
How to find the word?We know that the general linear equation can be written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
We know that if the line passes through (x₁, y₁) and (x₂, y₂) then the slope is:
s = (y₂ - y₁)/(x₂ - x₁)
With that formula we can get the slopes.
1) Using the points (0, 3) and (2, 4).
m = (4 - 3)/(2 - 0) = 1/2, so the letter is E.
2)Using (-1, -12) and (1, -8)
m = (-8 + 12)/(1 + 1) = 4/2 = 2, so the letter is C.
3) We have (2, -6) and (-4, -3) so:
m = (-3 + 6)/(-4 - 2) = 3/-6 = -1/2, so the letter is H
4)we can use the points (0, 3) and (1, 1), so:
m = (1 - 3)/(1 - 0) = -2, so the letter is A
Then the word is ECHA
Learn more about slopes at:
https://brainly.com/question/3493733
#SPJ1
Emma bought 7/8 yard of striped ribbon and 8/9 yard of solid ribbon which kind of ribbon did she buy more?
Answers
Answer:
She bought more of the solid ribbon.
Step-by-step explanation:
Let's look for the LCD
The common denominator is 72
So we have 63/72 and 64/72
Thus, 63/72 < 64/72.
Emma bought solid ribbons more as 8/9 is greater than 7.8.
What is a fraction?A fraction is written in the form of p/q, where q ≠ 0.
Fractions are of two types they are proper fractions in which the numerator is smaller than the denominator and improper fractions where the numerator is greater than the denominator.
Given, Emma bought 7/8 yards of striped ribbon and 8/9 yards of solid ribbon.
Now, The LCM of the denominators 8 and 9 is 72.
So, (7×9)/(8×9) and (8×8)/(9×8).
63/72 and 64/72.
As the numerator of the solid ribbon is greater the fraction 8/9 is greater.
So, She bought more solid ribbons.
learn more about fractions here :
https://brainly.com/question/10354322
#SPJ2
Simple math! What is the issue with my work? I got it wrong.
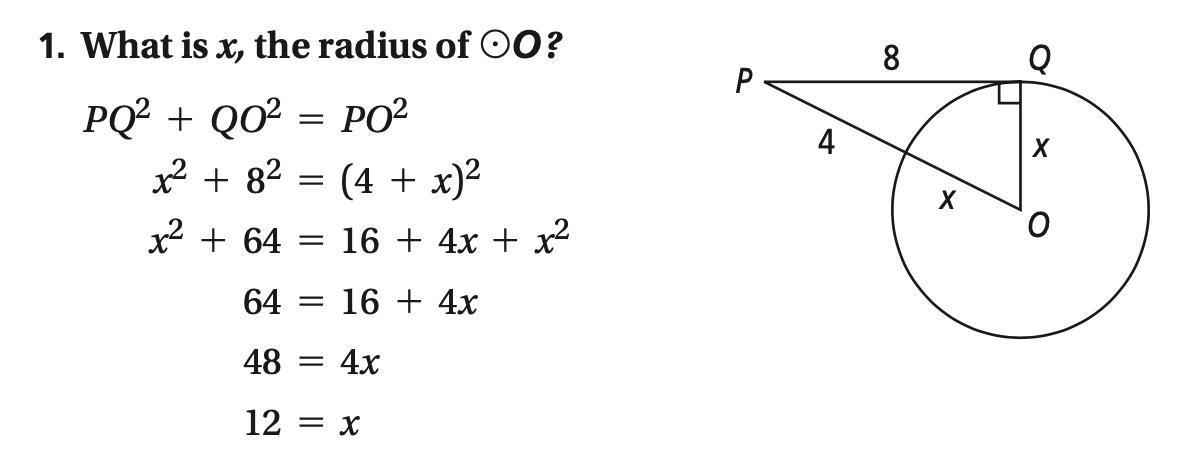
Answers
Answer:
x = 6
Step-by-step explanation:
In the third line of the solution on right side of the equal sign, middle term should be 8x instead of 4x.
The final value of x will be 6.
\( PQ^2 + QO^2 = PO^2 \\
x^2 + 8^2 = (4+x)^2 \\
x^2 + 64 = 16 + 8x + x^2 \\
64 = 16 + 8x \\
64 - 16 = 8x \\
48 = 8x \\
6 = x\\\)
A______ is a value, usually in the form of a letter or symbol, that can change or that represents an unknown quantity.
Answers
Answer:
Variable
Step-by-step explanation:
32 = 25t ^ 2 - 4 round to the nearest tenth
Answers
Answer:
t = 1.2, -1.2
32 + 4 = 25t^2
36 = 25t^2
Root of 36 = root of 25t
6 = 5t
6/5 = t
Therefore t = +-1/2 or +-6/5
Find the distance between points M(-3, -1) and N(2, 3) on the graph below. Round your
answer to the nearest tenth if necessary.

Answers
The distance between the points M(-3, -1) and N(2, 3) will be 3 Units.
We know the formula for calculating a distance between two given points. We call it the Distance formula which can be represented by the equation: \(d = \sqrt{(x_{2} - x_{1}) - (y_{2} - y_{1}) }\) , where d = Distance between two points. Now, M(-3, -1) = (x₁, y₁), and N(2, 3) = (x₂, y₂). Now, Putting these values in the Distance formula, we get :
=> \(d = \sqrt{(x_{2} - x_{1}) - (y_{2} - y_{1}) }\) => \(d = \sqrt{(2 - (-3) + (3 - (-1)}\)
=> \(d = \sqrt{(2 + 3) + (3 + 1)}\) => \(d = \sqrt{9}\)
=> d = 3 Units.
We get the distance d = 3 units by using the Distance formula.
Hence, the distance between two points M(-3, -1) and N(2, 3) calculated by the Distance formula will be 3 Units.
To know more about the Distance formula, Click here:
https://brainly.com/question/20758560
#SPJ9
I need some help with this problem

Answers
Answer:(-(3x^(3)-x-1))/((x^(2)+1)^(2))
3. You get three summer jobs to help you save for college expenses. In your job as a cashier,
you work 20 hours per week and earn $9.50 per hour. Your second and third jobs are at a local
hospital. There, you earn $9.00 per hour as a payroll clerk and $7.00 per hour as an aide. You
always work 10 hours less per week as an aide than you do as a payroll clerk. Your total weekly
salary depends on the number of hours you work at each job.
a. Determine the input and output variables for this situation.
b. Explain how you calculate the total amount earned each week.
c. If x represents the number of hours you work as a payroll clerk, represent the number of
hours you work as an aide in terms of x.
d. Write an equation that describes the total amount you earn each week. Use x to represent
the input variable and y to represent the output variable. Simplify the expression as much
as possible.
e. If you work 12 hours as a payroll clerk, how much will you make in one week?
f. What are the practical replacement values for x? Would 8 hours at your payroll job be a
realistic replacement value? What about 50 hours?
g. When you don't work as an aide, what is your total weekly salary?
Please help!
Answers
Hence the output variable (total weekly earnings) is a function of the input variable (number of hours worked as a payroll clerk) and may be expressed by the equation y = 16x + 120.
What is a Variable?A variable is anything that may be altered in the context of a mathematical notion or experiment. Variables are frequently denoted by a single symbol. .
a. Input variables: hours worked as a cashier, payroll clerk, and assistant.
The total amount earned each week is the output variable.
b. To determine the weekly total, multiply the number of hours worked at each job by the hourly rate and put them together. As a result, the equation would be:
Total weekly wage = (hours worked as a cashier x cashier hourly rate) + (hours worked as a payroll clerk x payroll clerk hourly rate) + (hours worked as an aide x rate per hour as an aide)
c. The amount of hours worked as an assistant is always 10 hours fewer than that of a payroll clerk. Therefore, if x denotes the number of hours worked as a payroll clerk, then the number of hours worked as an assistant may be denoted as (x - 10).
d. The equation describing the total money earned each week is as follows:
(20 x 9.5) + (x x 9) + ((x - 10) x 7) = y
This expression is simplified as follows:
y = 190 + 9x - 70 + 7x
y = 16x + 120
Hence the output variable (total weekly earnings) is a function of the input variable (number of hours worked as a payroll clerk) and may be expressed by the equation y = 16x + 120.
f. The realistic replacement values for x would be determined by the maximum number of hours you may work at each job as well as the amount of time available to work. Working 8 hours as a payroll clerk may be a reasonable substitute value if you have restricted availability, but 50 hours is unlikely.
g. If you do not work as an aide, you may calculate your total weekly income by setting the number of hours worked as an aide to zero in the calculation for the total amount earned each week. This results in:
y = 16x + 120 + 0
y = 16x + 120
As a result, the total weekly wage would be determined only by the number of hours performed as a cashier and payroll clerk.
To know more about variable visit:
https://brainly.com/question/2466865
#SPJ1
Please explain your answer to the question in the picture with steps.

Answers

what is the input set of a function called
Answers
Answer:
A function is a mathematical device that converts one value to another in a known way. ... The set of allowable inputs to a given function is called the domain of the function. The set of possible outputs is called the range of the function.
Step-by-step explanation:
Hopefully this was mindfull
The input set of a function is called the "Domain" of the function.
What is the range and domain of a function?A function's range is the set of all values that the function accepts, and its domain is the set of all values for which the function is defined.
The domain is for the independent variable while the range is for the dependent variable.
For any function, the values which we are putting form a set of intervals called domain.
For example f(x) = x²
Now if we put x = 1 then it is called as domain variable while the value of function at x = 1 its that f(1) = 1 called range variable.
Hence "The input set of a function is called the "Domain" of the function".
For more details about the range and domain of the function,
brainly.com/question/28135761
#SPJ6
please solve the question attached

Answers
1. Based on the producer theory, an increase in the demand for labor (L) would be caused by An increase in the productivity of labor, A decrease in the wage rate and A decrease in the rental rate of capital.
2. Missing variables in this simple producer theory would include The technology used to produce output, The preferences of consumers and Quality of labor and capital.
What more should you know about the producer thoery?In the standard producer theory, a producer minimizes costs for a given level of output.
This involves choosing the optimal mix of inputs, such as labor (L) and capital (K), to produce the desired output (y).
The cost function is represented by C = wL + rK, where w is the wage rate (cost of labor) and r is the rental rate (cost of capital).
Find more exercises on producer theory;
https://brainly.com/question/14441430
#SPJ1
Nadia says the hypotenuse of this right triangle has a length of 73 because the Pythagorean theorem states that (28 + 45) squared = 73 squared
Answers
Answer:
that is wrong
Step-by-step explanation:
28^2+45^2=2809
which is 53^2
Answer:
Wrong
Step-by-step explanation:
the Pythagorean theorem is x^2+y^2=z^2 Not (x+y)^2=z^2 so Nadia is wrong