Answers
Hello!
The slope equation is y = mx + b
mx is the slope and b is the yintercept.
4. y= -3x + 5
See where I put the slope and y intercept above?
Those are where the numbers go in that equation.
5. 3x + y = 5
The standard for equation is: Ax + by = c
y = -3x + 5
we need to make the equation look like the standard form equation.
y = -3x + 5
lets add 3x to both sides
The answer is 3x + y = 5
6. m = \(\frac{3}{2}\)
We need to use this formula: \(m=\frac{y2-y1}{x2-x1} \\\\\\\)
The points said are: (2, 5) and (4, 8)
\(m=\frac{8-5}{4-2}\)
m = 3/2
M is the slope.
---------------
I hope this helps,
Have a great day!!
Related Questions
if the length of the diagonal of a rectangular box must be l, use lagrange multipliers to find the largest possible volume.
Answers
Using Lagrange multipliers, the largest possible volume of a rectangular box can be found with a given diagonal length l.
Let's denote the dimensions of the rectangular box as length (L), width (W), and height (H). The volume (V) of the box is given by V = LWH. The constraint equation is the Pythagorean theorem: L² + W² + H² = l², where l is the given diagonal length.
To find the largest possible volume, we can set up the following optimization problem: maximize the volume function V = LWH subject to the constraint equation L² + W² + H² = l².
Using Lagrange multipliers, we introduce a new variable λ (lambda) and set up the Lagrangian function:
L = V + λ(L² + W² + H² - l²).
Next, we take partial derivatives of L with respect to L, W, H, and λ, and set them equal to zero to find critical points. Solving these equations simultaneously, we obtain the values of L, W, H, and λ.
By analyzing these critical points, we can determine whether they correspond to a maximum or minimum volume. The critical point that maximizes the volume will give us the largest possible volume of the rectangular box with a diagonal length l.
By utilizing Lagrange multipliers, we can optimize the volume function while satisfying the constraint equation, enabling us to determine the dimensions of the rectangular box that yield the maximum volume for a given diagonal length.
Learn more about Lagrange multipliers here:
https://brainly.com/question/30776684
#SPJ11
Please help.
Is algebra.
PLEASE HELP NO LINKS OR FILES.
I don't want links.

Answers
Answer:
question 12 is answer B
question 13 is -8x^3
Step-by-step explanation:
exponent rule \(\frac{a^m}{a^n} = a^(^m^-^n^)\)
an art teacher has a 2-pound block of clay into 5 equal pieces. what is the weight, in pounds, of each piece of clay?
Answers
Answer:
0.4lb
Step-by-step explanation:
Take 2lb and convert it to ounces only. That is a total of 32oz. Divide 32oz by 5 and you get 6.4oz per piece of clay. Now convert the 6.4oz back to pounds; 0.4lb.
what is the opposite of 18
Answers
Answer:
-18
Step-by-step explanation:
-18
Explanation:
Solve for c law of sines

Answers
Answer:
c/sin(60°) = 14/sin(25°)
c = 14sin(60°)/sin(25°) = 28.7
Let X = {a, b, c) and A = {4, X, {a}, {b,c}}, Ag = {4, X, {b}, {a, c}} be two o-algebras over X. Then a. An.A, is not a o-algebra over X. b. An A, is a o-algebra over X and A, UA, is not a g-algebra over X. c. A, UA, is a o-algebra over X. d. None of the above. O O b. e. O d. a Let (X, 4) be a measurable space and let f, g: X → R be two mea- surable functions. Which of the following statements is false? a. 52 . 108>1] + \S1g
Answers
An A is a -algebra over X and A ∪ Ag is not a -algebra over X.
In this case, let's analyze the properties of the sets in question:
X = {a, b, c}
A = {4, X, {a}, {b, c}}
Ag = {4, X, {b}, {a, c}}
To determine if An A is a -algebra over X, we need to check if it satisfies the three conditions of a -algebra:
1. X ∈ An A: In this case, X = {a, b, c} ∈ An A, since X is a subset of itself.
2. An A is closed under complementation: For any set E ∈ An A, we need to ensure that its complement, X \ E, is also in An A. Let's check the sets in A:
- {4} ∈ An A: The complement is X \ {4} = {a, b, c}, which is not in An A.
- X ∈ An A: The complement is X \ X = ∅, which is in An A.
- {a} ∈ An A: The complement is X \ {a} = {b, c}, which is in An A.
- {b, c} ∈ An A: The complement is X \ {b, c} = {a}, which is in An A.
Since not all sets in A have complements in An A, An A is not closed under complementation and therefore not a -algebra over X.
Now let's analyze A ∪ Ag to determine if it is a -algebra over X:
1. X ∈ A ∪ Ag: Since X is a subset of itself, X ∈ A ∪ Ag.
2. A ∪ Ag is closed under complementation: For any set E ∈ A ∪ Ag, we need to ensure that its complement, X \ E, is also in A ∪ Ag. Let's check the sets in A and Ag:
- {4} ∈ A ∪ Ag: The complement is X \ {4} = {a, b, c}, which is in A ∪ Ag.
- X ∈ A ∪ Ag: The complement is X \ X = ∅, which is in A ∪ Ag.
- {a} ∈ A ∪ Ag: The complement is X \ {a} = {b, c}, which is in A ∪ Ag.
- {b, c} ∈ A ∪ Ag: The complement is X \ {b, c} = {a}, which is in A ∪ Ag.
Since all sets in A and Ag have complements in A ∪ Ag, A ∪ Ag is closed under complementation and is a -algebra over X.
In conclusion, option b is the correct answer: An A is a -algebra over X, and A ∪ Ag is not a -algebra over X.
To know more about -algebras, refer here:
https://brainly.com/question/32611431#
#SPJ11
Evaluate 7r- 15/8 when r= 3 and 8=5. I'm confused need help:)
Answers
the graph of y=f(x) is shown below. what are all of the real solutions of f(x)=0
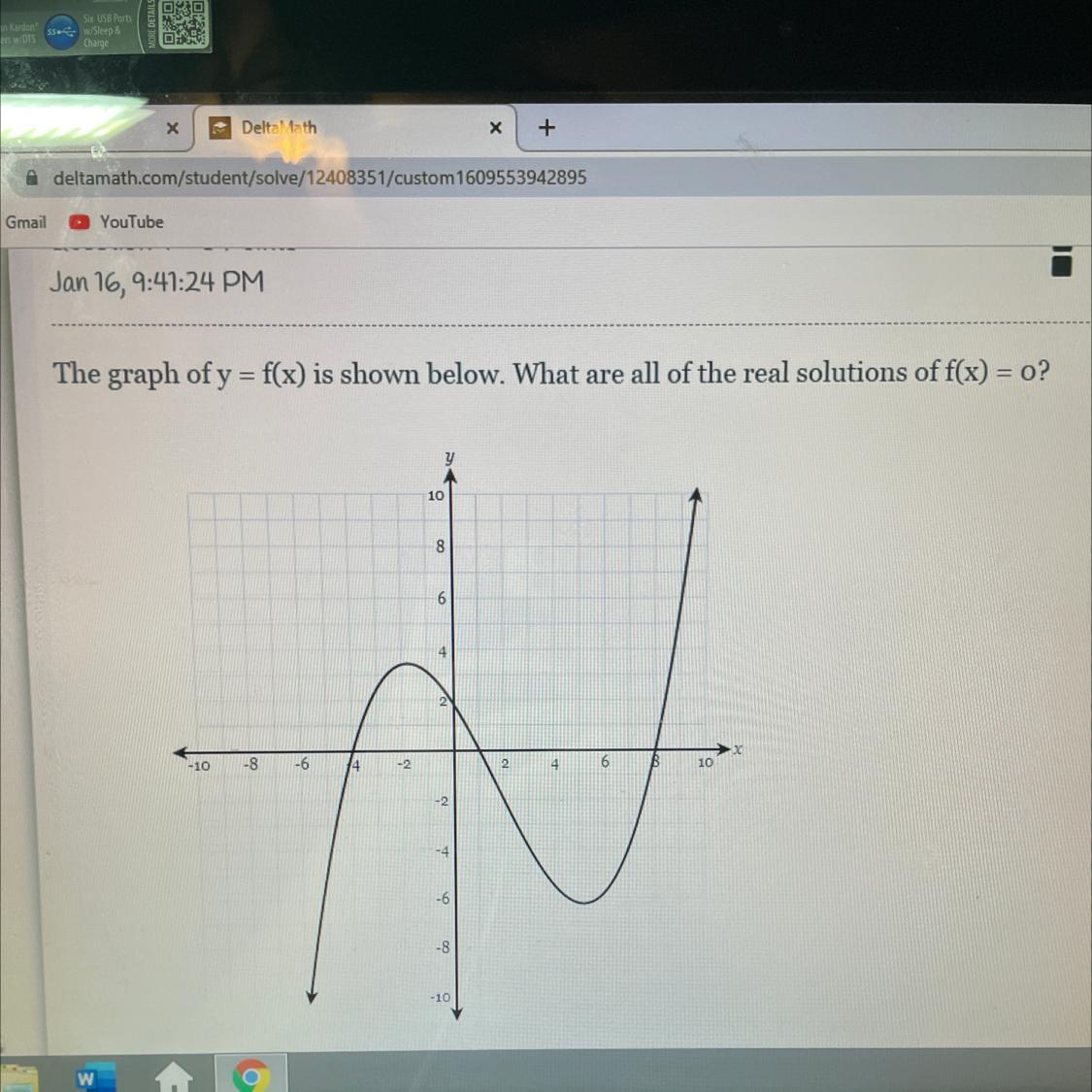
Answers
All real solutions of the function y=f(x) are x = -4 and x = 4
What is a solution ?Suppose that we've a function y = f(x) such that f(x) is quadratic.
When y = 0, then the values of x for which f(x) = 0 is called solution of quadratic equation f(x) = 0. These solution gives values of x, and when we plot x and f(x), we'd see that the graph intersects the x-axis at its solution points.
we are Given graph in the attachment represents the function y = f(x)
Since Real solutions of the function shows all the points where the curve of the graph either touches or crosses the x-axis.
Thus the graph of the function touches and crosses at x = -4 and x = 4
Therefore, all real solutions of the function y=f(x) are x = -4 and x = 4
Learn more about solutions of a equation here:
https://brainly.com/question/15582302
#SPJ5
prove the following
(Q,+,*) is a field
(Z5, circle plus, circle dot) is a field
(z4, circle plus, circle dot) is not a field
Answers
The multiplicative inverse does not exist for every element other than 0. Therefore, it violates one of the field's requirements for being a field.A field is a mathematical structure that is defined as a set of elements on which two operations are performed. A field, in general, is a mathematical structure that is defined as a set of elements on which two operations are performed:
addition and multiplication. To demonstrate that a structure is a field, we must show that the following criteria hold:Closure under addition and multiplication: For all a and b in the field, a+b and a * b are also in the field. Associativity of addition and multiplication: For all a, b and c in the field, a + (b + c) = (a + b) + c and a(bc) = (ab)c.Commutativity of addition and multiplication: For all a and b in the field, a + b = b + a and ab = ba. Existence of an identity element for addition and multiplication: There exist two distinct elements, 0 and 1, in the field such that a+0 = a and a*1 = a for all a in the field. Existence of additive and multiplicative inverses:
For every element a in the field other than 0, there exists an element -a such that a + (-a) = 0, and for every element a in the field other than 0, there exists an element a-1 such that a*a-1 = 1. Distributivity of multiplication over addition: For all a, b and c in the field, a(b + c) = ab + ac and (a + b)c = ac + bc.(Q,+,*) is a field.The set of rational numbers, Q, along with the usual addition and multiplication operations, is a field, which satisfies all the criteria for being a field.(Z5, circle plus, circle dot) is a field.The set of integers modulo 5, Z5, with the addition modulo 5 and multiplication modulo 5, is a field that satisfies all the criteria for being a field.(Z4, circle plus, circle dot) is not a field.The set of integers modulo 4, Z4, with the addition modulo 4 and multiplication modulo 4, is not a field because the multiplicative inverse does not exist for every element other than 0. Therefore, it violates one of the field's requirements for being a field.
To know more about factorization visit:
https://brainly.com/question/25998167
#SPJ11
OAB is a sector of a circle.
Calculate the radius of the circle to 2 d.p.
B.
131°
cm
192 cm
Not drawn accurately

Answers
The radius of the circle is 83.91 cm
How to determine the radius of the circleFrom the question, we have the following parameters that can be used in our computation:
Angle = 131 degrees
LEngth of arc = 192 cm
The length of arc is calcuulated as
Length = Angle/360 * 2pi r
Substitute the known values in the above equation, so, we have the following representation
131/360 * 2 * 22/7 * r = 192
So, we have
r = (192 * 7 * 360)/(131 * 2 * 22)
Evaluate
r = 83.91
Hence, the radius is 83.91 cm
Read more about arc length at
https://brainly.com/question/2005046
#SPJ1
What is the probability of a student getting candy at the end of the maze? a. show step by step how you calculated the probability and tell which of the 2 models you used and why.
Answers
The probability of getting candy is 1/5.
Let's assume that there are 5 possible paths to take in the maze and only 1 of those paths leads to the candy.
Therefore, the probability of a student getting candy at the end of the maze is:
1/5 or 0.2 or 20%.
We used the classical probability model because there are a limited number of possible outcomes that are equally likely to occur.
In this case, the probability of getting candy is the ratio of favorable outcomes (1) to total outcomes (5).
Therefore, the probability of getting candy is 1/5.
https://brainly.com/question/31828911?referrer=searchResults
#SPJ11
work out 11. 28- 2.843
Answers
Answer:
25.157
Step-by-step explanation:
28-2.843=25.157
What is the answer please help

Answers
Answer: 352
Step-by-step explanation:
Answer:
352
Step-by-step explanation:
hard to explain
find the last common denominator for these two rational expressions

Answers
Answer:
Least common denominator = (x - 1)²(x - 2)
Step-by-step explanation:
Least common denominator of two rational expressions = LCM of the denominator of the expressions.
\(\frac{x^3}{x^2-2x+1}\) and \(\frac{-3}{x^{2}-3x+2}\)
Factorize the denominators of these rational expressions,
Since, \(x^{2}-2x+1\) = x² - 2x + 1
= (x - 1)²
And x² - 3x + 2 = x² - 2x - x + 2
= x(x - 2) -1(x - 2)
= (x - 1)(x - 2)
Now LCM of the denominators = (x - 1)²(x - 2)
Therefore, Least common denominator will be (x - 1)²(x - 2).
Solve the following system of linear equations by graphing:-X+ y = -74x + 4y = 20
Answers
1) Let's solve this Linear System, using the method of Elimination/Addition
-x+y=-7 Multi
4x+4y = 20
rotate the triangle through 180 degrees about the origin?
Answers
Answer:
Step-by-step explanation:
Solve the inequality.
|3x+7| <_ 4

Answers
Step-by-step explanation:
it can be written as. -4<_(3x+7)<_4
= -11 <_(3x) <_ (-3)
= (-11/3) <_ X <_ (-1)
Given that y varies inversely with x, if x =7 and y = 4, what is y when x = 2?
Answers
Answer:
y = 14
Step-by-step explanation:
y ∝ \(\frac{1}{x}\)
=> y = \(\frac{k}{x}\) -------------(1)
Where k is the constant of proportionality
Now,
x = 7, y = 4
Putting in (1)
4 = \(\frac{k}{7}\)
So,
=> k = 28
Now y = ? when x = 2
Putting x and k in (i)
y = \(\frac{28}{2}\)
y = 14
Answer:
\(y=14\)
Step-by-step explanation:
\(y \propto 1/x\)
\(y=k/x\)
\(4=k/7\)
\(4 \times 7 = k\)
\(28=k\)
\(y=28/x\)
\(y=28/(2)\)
\(y=14\)
On the unit circle, where 0 < theta < or equal to 2pi, when is tan theta undefined?
A. Theta=pi and theta=2pi
B. sin theta = cos theta
C. theta = pi/2 and theta=3pi/2
D. sin theta = 1/cos theta
Answers
Therefore, the answer is option C: theta = pi/2 and theta = 3pi/2.
To determine when tan(theta) is undefined on the unit circle, we need to remember the definition of the tangent function.
Tangent is defined as the ratio of the sine and cosine of an angle. Specifically, tan(theta) = sin(theta)/cos(theta).
Now, we know that cosine can never be equal to zero on the unit circle, since it represents the x-coordinate of a point on the circle and the circle never crosses the x-axis. Therefore, the only way for tan(theta) to be undefined is if the cosine of theta is equal to zero.
There are two values of theta on the unit circle where cosine is equal to zero: pi/2 and 3pi/2.
At theta = pi/2, we have cos(pi/2) = 0, which means that tan(pi/2) = sin(pi/2)/cos(pi/2) is undefined.
Similarly, at theta = 3pi/2, we have cos(3pi/2) = 0, which means that tan(3pi/2) = sin(3pi/2)/cos(3pi/2) is also undefined.
Therefore, the answer is option C: theta = pi/2 and theta = 3pi/2.
To know more about theta visit:-
https://brainly.com/question/21807202
#SPJ11
What is the number of possible options for each situation?

Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the method of getting possible options.
When asked to find the number of possible options, this is a permutation problem. Therefore, we use the permutation formula.
\(^nP_r=\frac{n!}{(n-r)!}\)STEP 2: Solve the first question
\(\begin{gathered} ^nP_r=\frac{n!}{(n-r)!} \\ For\text{ the first question, n=}45,r=3 \\ ^{45}P_3=\frac{45!}{(45-3)!}=\frac{45!}{42!}=\frac{45\times44\times43\times42!}{42!} \\ \Rightarrow45\times44\times43=85140 \end{gathered}\)There are 85140 possible options.
STEP 3: Solve the second question
\(\begin{gathered} ^nP_r=\frac{n!}{(n-r)!} \\ n=7,r=5 \\ ^7P_5=\frac{7!}{(7-5)!}=\frac{7!}{2!}=2520 \end{gathered}\)There are 2520 possible options.
STEP 4: Solve the third question.
\(\begin{gathered} ^nP_r=\frac{n!}{(n-r)!} \\ n=11,r=9 \\ ^{11}P_9=\frac{11!}{(11-9)!}=\frac{11!}{2!}=19958400 \end{gathered}\)There are 19958400 possible options.
STEP 5: Solve the fourth question
\(\begin{gathered} ^nP_r=\frac{n!}{(n-r)!} \\ n=20,r=4 \\ ^{20}P_4=\frac{20!}{(20-4)!}=\frac{20!}{16!}=\frac{20\times19\times18\times17\times16!}{16!}=20\times19\times18\times17=116280 \end{gathered}\)There are 116280 possible options
three boxes under my stairs contain apples or pears are both each box contains the same number of pieces of fruit the first box contains all 12 of the apples and 1 /9th of the pears how much of the fruit are there in each box
Answers
There are 16 fruits in each of the boxes found under the stairs.
What is an equation?An equation is an expression used to show the relationship between two or more numbers and variables.
Let x represent the number of pears, hence:
Number of fruit in first box = 12 + (1/9)x
Number of fruit in second box = number of fruit in third box = (8/9)x ÷ 2 = (4/9)x
Therefore:
12 + (1/9)x = (4/9)x
x = 36
First box = second box = third box = (4/9) * 36 = 16
There are 16 fruits in each of the boxes found under the stairs.
Find out more on equation at: https://brainly.com/question/2972832
PLZ HELP QUICK............

Answers
Answer:
\(4^m\)
Step-by-step explanation:
When you exponent an exponent, you multiply the powers together.
When you divide exponents, you subtract the powers.
Step 1: Convert to same base
log₄64 = 3
Step 2: Rewrite equation
\(\frac{(4^3)^{0.5m}}{4^{0.5m}}\)
Step 3: Simplify
\(\frac{4^{1.5m}}{4^{0.5m}}\)
Step 4: Simplify
\(4^m\)
i need help please
The entire basis of a whaling attack is to appeal to as many companies as possible at the same time, therefore increasing the likelihood that one will "take the bait." appear as authentic as possible
Answers
Staying vigilant and maintaining a healthy skepticism towards unexpected or unusual requests can go a long way in protecting against whaling attacks.
Whaling attacks, also known as CEO fraud or business email compromise (BEC), involve targeting high-level executives or individuals with authority in organizations.
To make their attacks appear authentic, attackers employ various techniques. Here are some common strategies used in whaling attacks:
1. Social Engineering: Attackers research their targets extensively to gather information about the targeted organization, executives, and employees. This information is then used to craft personalized and convincing messages that appear legitimate.
2. Email Spoofing: Attackers may forge or manipulate email headers to make it appear as if the email is coming from a trusted source or a high-level executive within the organization.
They might use email addresses that closely resemble the legitimate ones, with only minor differences that can be easily overlooked.
3. Branding and Logos: Whaling emails often incorporate company logos, email signatures, and other branding elements to create a sense of familiarity and authenticity.
These visual cues can trick recipients into believing that the email is genuinely from a trusted source within the organization.
4. Urgency and Confidentiality: Attackers leverage psychological tactics by creating a sense of urgency or emphasizing the confidential nature of the communication.
They may claim the need for immediate action or request that the recipient keeps the information confidential, increasing the chances of the target complying without thoroughly verifying the request.
5. Manipulation of Authority: Whaling attacks often involve impersonating executives or individuals in positions of authority within an organization.
By mimicking the communication style and language used by executives, attackers attempt to create an illusion of legitimacy and persuade the target to comply with their requests.
To protect against whaling attacks, organizations can implement the following measures:
1. Employee Training and Awareness: Conduct regular training sessions to educate employees about the risks associated with whaling attacks. Train them to be vigilant and to verify any unusual requests, especially those related to financial transactions or sensitive information.
2. Strong Authentication Practices: Implement multi-factor authentication (MFA) for email and other critical systems. This adds an extra layer of security and makes it harder for attackers to gain unauthorized access to accounts.
3. Robust Email Security: Deploy email security solutions that can detect and block spoofed or suspicious emails. These solutions often use advanced threat intelligence and machine learning algorithms to identify and prevent whaling attacks.
4. Verify Requests: Encourage employees to verify requests for fund transfers, sensitive information, or other unusual actions by using secondary communication channels such as phone calls or in-person conversations. It's crucial to establish clear protocols for verifying such requests.
5. Incident Response Planning: Develop an incident response plan that outlines the steps to be taken in case of a suspected whaling attack. This plan should include procedures for reporting incidents, conducting investigations, and mitigating the impact of successful attacks.
To know more about whaling attacks refer here:
https://brainly.com/question/29971956
#SPJ11
What is the range of possible sizes for side x?

Answers
Answer:
Should be 3.9
Step-by-step explanation:
prove me wrong
Compound X has a solubility of 20 g in 100 g of water at 20°C. What is the minimum amount of water needed to dissolve 50 g of compound X? 250 g 100 g 500 g 200 g
Answers
Answer:
250 g of water
find the relative maxima and relative minima, if any, of the function. (if an answer does not exist, enter dne.) g(x)
Answers
The relative maxima and minima of the function g(x) are at the point (-4, 22) at the local maxima and at point (4,-124) at the local minima.
Given:
Function g(x) = x^3 - 48x + 4
Take the derivative and set it equal to zero
3x^2 - 48 = 0
x^2 = 48/3 = 16
x = sqr16 = ±4
At x=+4, y = (4)^3 -48(4) + 4 = 64 -192+4 = -124
Point (4,-124) is a local or relative minimum
At x-4 y=(-4)^3 -48(-4)+4 = -64 + 192 + 4 = 122
The point (-4, 22) is a local or relative maximum
Refer to this complete question:
Find the relative maxima and minima, if any, of the function. (If an answer does not exist, enter DNE.) f(x) = x3 − 48x + 4 relative maximum (x, y) = relative minimum (x, y) =?
To know more about the maxima and minima visit: https://brainly.com/question/29562544
#SPJ4
I need help Factoring: 2x^3 + 11x + 15
Answers
The factored form of 2x^3 + 11x + 15 is:
(2x + 1)(x^2 + 5) + 15
Factoring 2x^3 + 11xTo factor 2x^3 + 11x + 15, we need to find two binomials that multiply to give us the expression.
One way to approach this is to use a method called grouping. We can first group the first two terms and the last two terms:
2x^3 + 11x + 15 = (2x^3 + 10x) + (x + 15)
Notice that we factored out a common factor of 2x from the first two terms, and a common factor of 1 from the last two terms.
Next, we can factor each group separately:
2x^3 + 10x = 2x(x^2 + 5)
x + 15 = 1(x + 15)
Putting these factors together, we get:
2x^3 + 11x + 15 = 2x(x^2 + 5) + 1(x + 15)
Therefore, the factored form of 2x^3 + 11x + 15 is:
(2x + 1)(x^2 + 5) + 15
Learn more on factorisation here
https://brainly.com/question/10718512
#SPJ1
Beth added 1 1/4
pounds of fruit to a fruit basket. Her son took 2 3/8 pounds
of fruit out of the basket. What was the total change in pounds of fruit in the
fruit basket?
Answers
Answer: To find the total change in pounds of fruit in the basket, we need to subtract the amount taken out from the amount added.
First, let's convert all the fractions to decimals:
1 1/4 = 1.25
2 3/8 = 2.375
Now, we can subtract:
1.25 - 2.375 = -1.125
So, the total change in the fruit basket was -1.125 pounds, meaning the basket had 1.125 pounds less fruit after the removal.
Step-by-step explanation:
Choose the correct classification of 2x4 − 8x5 − 2x2 5.
Answers
Answer: The correct classification of 2x4 - 8x5 - 2x2 + 5 is 5th-degree polynomial.
We know that the highest exponent of a polynomial is called the degree of the polynomial.
The highest degree of the given polynomial is 5. Hence, from the above-written concepts, we can say that the degree of the polynomial is 5.
Thus, the polynomial is a 5th-degree polynomial.
Step-by-step explanation:
If there are 2 blue, 5 yellow, and 3
white marbles in a bag, what is the
probability of pulling a blue marble
a
from the bag?
