Answers
Related Questions
Write the equation of the line that passes through
(6,-7) and is perpendicular to y = 2/3x+1.
Answers
Answer:
Step-by-step explanation:
y = (2/3)x + 1
m = 2/3
The slope of the perpendicular line = -1/m
\(Slope = \dfrac{-1}{\dfrac{2}{3}}=-1*\dfrac{3}{2}=\dfrac{-3}{2}\\\\\\(6,-7) ; \ x_{1}= 6 \ ; y_{1} = -7\\\\\\Equation: y-y_{1}=m(x-x_{1})\\\\\\y -[-7] = \dfrac{-3}{2}(x - 6)\\\\\\y + 7 = \dfrac{-3}{2}x - 6*\dfrac{-3}{2}\\\\y +7=\dfrac{-3}{2}x+9\\\\y = \dfrac{-3}{2}x+9-7\\\\y =\dfrac{-3}{2}x+2\)
Please help!!! I will mark brainliest! Explain your answers please!!! (If you dont know then dont awnser)


Answers
Answer:
Step-by-step explanation:
Angle ACB is congruent to Angle DCE
Reason 4: SAS- Side Angle Side
Angle ACB is congruent to Angle DCE
Reason 4: SAS- Side Angle Side is the correct answer to the question
Please help or else I’m gonna get in trouble please im scared NOw Help please
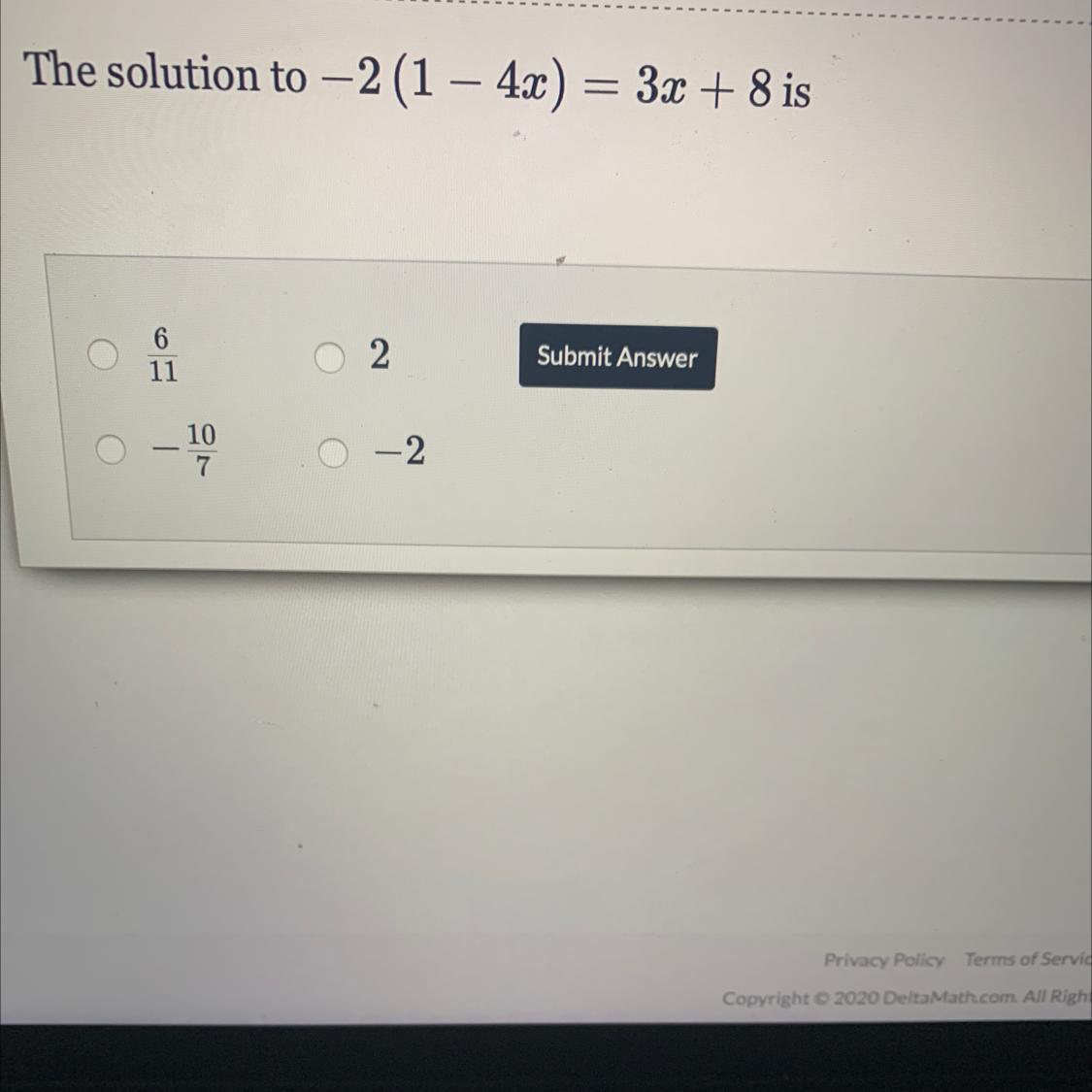
Answers
Answer:
\(-2(1 - 4x) = 3x + 8\\\\-2 + 8x = 3x + 8\\\\-2 + 5x = 8\\\\5x = -10\\\\x = -2\)
(3) Consider basis B = {u} = (21)", u = (1 217). Find the matrix representation with respect to B for the transformation of the plane that rotates the plane radians counter-clockwise by doing the following: (a) Find matrix M that will transform a vector in the basis B into a vector in the standard basis. (b) Find the matrix representations of the transformation described above with re- spect to the standard basis. (c) Use M and M- to convert the matrix representation of transformation you found in part (b) into a matrix representation with respect to basis B.
Answers
a) The matrix M that transforms the basis vector u into the standard basis is M = [1 0 0; 0 1 0; 0 0 1]
b) The transformation that rotates the plane counterclockwise by θ radians can be represented matrix R = [cos(θ) -sin(θ); sin(θ) cos(θ)]
c) The rotation transformation with respect to the standard basis:
[R]B = [R] = [cos(θ) -sin(θ); sin(θ) cos(θ)]
How to find matrix M that transforms a vector in basis B into a vector in the standard basis?To find the matrix representation of the transformation that rotates the plane by θ radians counterclockwise with respect to the given basis B = {u}, we'll follow the steps outlined in the question.
(a) Find matrix M that transforms a vector in basis B into a vector in the standard basis:
To find M, we need to express the basis vector u = (1, 2, 17) in the standard basis. We can achieve this by writing u as a linear combination of the standard basis vectors e1, e2, and e3.
u = (1, 2, 17) = x * e1 + y * e2 + z * e3
To determine x, y, and z, we solve the following system of equations:
1 = x
2 = 2y
17 = 17z
From these equations, we find x = 1, y = 1, and z = 1. Therefore, the matrix M that transforms the basis vector u into the standard basis is:
M = [1 0 0; 0 1 0; 0 0 1]
How to find the matrix representations of the transformation with respect to the standard basis?(b) Find the matrix representations of the transformation with respect to the standard basis:
The transformation that rotates the plane can be represented by the following matrix:
R = [cos(θ) -sin(θ); sin(θ) cos(θ)]
How to use M and M-1 to convert the matrix representation of the transformation into a representation with respect to basis B?(c) Use M and M-1 to convert the matrix representation of the transformation into a representation with respect to basis B:
To find the matrix representation of the transformation with respect to basis B, we use the formula:
\([M]B = [M] * [R] * [M]^-1\)
where [M] is the matrix representation of the basis transformation from basis B to the standard basis, [R] is the matrix representation of the transformation with respect to the standard basis, and \([M]^-1\) is the inverse of [M].
Since we already found M in part (a) as the identity matrix, we have:
\([M] = [M]^-1 = I\)
Therefore, the matrix representation of the transformation with respect to basis B is [R]B = [I] * [R] * [I] = [R]
So the matrix representation of the rotation transformation with respect to basis B is the same as the matrix representation of the rotation transformation with respect to the standard basis:
[R]B = [R] = [cos(θ) -sin(θ); sin(θ) cos(θ)]
Learn more about matrix representations and transformations
brainly.com/question/32202731
#SPJ11
4x-2*(3x-2)+3x solve for x
Answers
Hey there!
4x - 2 * (3x - 2) + 3x
= 4x - 2(3x - 2) + 3x
= 4x - 2(3x) - 2(-2) + 3x
= 4x - 6x + 4 + 3x
= -2x + 4 + 3x
= 1x + 4
= x + 4
Therefore, your answer is: x + 4
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
Find the area of the following shapes

Answers
Answer:
Area = 114 m2
Step-by-step explanation:
Area of the Figure = Area of Rectangle ABCD - Area of Rectangle HGFE
Area of the Figure = 12*14 - 9*6 = 168 - 54 = 114
f(x)=log5x what Is the range of the function
Answers
The range of the function f(x) = log5x is (-∞, +∞).The function f(x) = log5x represents the logarithm base 5 of x. To determine the range of this function, we need to consider the possible values that the logarithm can take.
The range of the logarithm function y = log5x consists of all real numbers. The logarithm function is defined for positive real numbers, and as x approaches 0 from the positive side, the logarithm approaches negative infinity. As x increases, the logarithm function approaches positive infinity.
The range of the function is the set of all possible output values. In this case, the range consists of all real numbers that can be obtained by evaluating the logarithm
log5(�)log 5 (x) for �>0 x>0.
Since the base of the logarithm is 5, the function log5x will take on all real values from negative infinity to positive infinity. Therefore, the range of the function f(x) = log5x is (-∞, +∞).
In other words, the function can output any real number, ranging from negative infinity to positive infinity. It does not have any restrictions on the possible values of its output.
For more such questions on Logarithm:
https://brainly.com/question/31117877
#SPJ8
Answer: All real numbers
Step-by-step explanation:
Edge
hey whats the answer to this?

Answers
a) The amount of water in the tank will be 0 after 5 minutes.
b) As time increases, the amount of water decreases at a rate of -60 L/min.
At which time the water reaches 0 liters?Here we can see a graph of a linear function that relates the amount of water in an aquarium (vertical axis) with the time (horizontal axis).
The amount of water in the aquarium will reach the 0 liters mark when the line intercepts the x-axis.
We can see that happens for x = 5 minutes
b) We can see that as we move to the right (time flows to the right in that graph) the line goes downwards. This means that the amount of water on the tank decreases as the time increases.
We can see that in 5 minutes, the amount of water goes from 300 lites to 0 liters, so the rate at which the water comes out of the tank is:
R = 300L/5min = 60 liters per minute.
It should actually be written with a negative sign so we are 100% clear that it means that the water is coming out from the tank, so the rate is:
R = -60 L/min
Learn more about linear equations:
https://brainly.com/question/4074386
#SPJ1
Suppose you have a rectangle with length 90 units and width 26 units. Each turn, you cut off the greatest possible square from the rectangle. You do so until you have only squares. How many squares will you get
Answers
We have cut out a total of 29370 squares.
First, let's find the greatest possible square that can be cut from the rectangle. This square will have a side length equal to the width of the rectangle, which is 26 units.
After cutting this square from the rectangle, we are left with a smaller rectangle that measures 90 units by (90-26=) 64 units.\
Now we repeat the process and cut out the largest possible square, which has a side length of 64 units.
After cutting out this square, we are left with a rectangle that measures 64 units by (64-26=) 38 units.
We continue this process until we can no longer cut out any more squares.
The side length of the remaining rectangle will be the length of the last square that we cut out.
Let's call this side length x.
At this point, the length of the rectangle is equal to the width, so:
90 - 26 - 64 - 38 - ... - x = x.
Simplifying this equation, we get:
(90 - 26 - 64 - 38 - ...) + x = x
2x = 90 - 26 - 64 - 38 - ...
2x = 90 - (26 + 64 + 38 + ...)
2x = 90 - (26 + 64 + 38 + 26 + 16 + 4 + 2)
2x = 90 - 176
2x = -86
x = -43
Since x cannot be negative, we know that we cannot cut out any more squares.
Therefore, we have cut out a total of:
\(26^2 + 64^2 + 38^2 + ... + (-43)^2\)
To calculate this sum, we can use the formula for the sum of the squares of the first n natural numbers:
\(1^2 + 2^2 + 3^2 + ... + n^2 = n(n+1)(2n+1)/6.\)
We need to find the value of n such that \(n^2\) is equal to \(43^2\)or the closest perfect square below it, which is \(42^2\).
We have:
\(42^2 = 1764.\)
\(43^2 = 1849\)
So n is equal to 42.
Therefore, the sum of the squares of the squares we have cut out is:
\(26^2 + 64^2 + 38^2 + ... + (-43)^2 = 26^2 + 64^2 + 38^2 + ... + 42^2\)
\(= 1^2 + 2^2 + 3^2 + ... + 42^2 - (1^2 + 2^2 + 3^2 + ... + 25^2)\)
\(= 42(42+1)(242+1)/6 - 25(25+1)(225+1)/6.\)
= 29370.
For similar question on square.
https://brainly.com/question/29271010
#SPJ11
What is the area, in square centimeters, of the trapezoid below?
11.7 cm
5.5 cm
6.5 cm

Answers
Answer:
50.05 cm^2
Step-by-step explanation:
Ok so first lets find the area of the rectangle before finding the attached triangle. You have to imagine a line separating this shape into a triangle and rectangle.
The rectangle's size is 6.5x5.5=35.75 cm^2
The rectangle's size is 11.7-6.5 to get the base length, which is 5.2
The height is 5.5
So it's 5.2*5.5/2=14.3 cm^2
14.3+35.75=50.05 cm^2
What would an 18% increase of 90 be?
Answers
Answer:
106.2
Step-by-step explanation:
A 18% increase of a number is the same as multiplying it by 1.18.
If we multiply 90 by 1.18 we get:
90 * 1.18
106.2
106.20.
The base of a triangle is (2x + 5) cm. If the area of the triangle is (2xy + 18x + 5y +45) cm² and the height is more than 30 cm, find the possible range of values of y.
Answers
Step-by-step explanation:
What is a computer ?♡?×_×7×^××:×::×:+^++^+_+
A rock is dropped from a bridge 320 feet above a river. The pathway that the rock takes can be modeled by the equation h=-16t squared+320. How long will it take the rock to reach the river?
A. 2.5 sec
B. 3.5 sec
C. 3.8 sec
D. 4.5 sec
Answers
Answer:
D. 4.5 sec
Step-by-step explanation:
Once the rock is on the ground it has no height (h=0)
h = -16t² + 320
0 = -16t² + 320
16t² = 320
t² = 20
t² = 20
t = √20
t= √4x5
t = 2√5
around 4.5 seconds
Find the volume of the cone.
Either enter an exact answer in terms of π or use 3.14 for π and round your final answer to the
nearest hundredth.

Answers
The answer is 48π units³ or 150.72 units³.
To find the volume of the cone, use the formula : 1/3 × πr²h
We are given that r = 6 and h = 4.
Solving :
V = 1/3 × π × 6² × 4V = 12 × 4 × πV = 48π units³ (in terms of π)V = 150.72 units³John earned $12 a day for babysitting his siblings after school each weekday (he did not babysit on weekends). He liked to have a small amount of money to spend on treats at the school canteen that his parents refuse to buy, but he also wanted to build up some savings. John decided to put a fraction of his earnings into a jar straight away. He spent all the rest on canteen treats.
How much money did John earn over a nine week term?
After 9 weeks, John had $378 in his jar. What percentage of his money did he save?
Answers
Answer:
He earns $540
70% of his money went to savings
Step-by-step explanation:
9 weeks x 5 days a week = 45 days
45 days x $12 a day = $540
378 * 100 / 540 = (378*100) / 540 = 37800/540 = %70
a map has a scale of 1/2 inches:12 miles if the actual distance between the cities is 480 miles how far apart are they on the map
Answers
Answer:
20 inches
Step-by-step explanation:
Since there are 480 miles in total, we have to divide it by 12 so we can see how many half inches that would be.
480÷12 = 40
That would mean you can fit forty 12's in 480. Since 12 miles equals 1/2, you would multiply it by 40.
1/2 × 40 =20
This means that the distance between the cities on the map would be 20 inches.
what is the fraction for 33%
decimal for 33%
Answers
\(Question\)
what is the fraction for 33%and the decimal for 33%?
Answer:
Your Answer Would Be \(\frac{33}{100}\) For your Fraction And For your Decimal It Would Be 0.33
Hope this Helps!
\(xXxAnimexXx\)
write an algebraic expression for each verbal expression. four more than the product of six and a number q
Answers
the value of the expression. -5.6 - ( 3.4 - 6.8)
Answers
Answer:
-2.2
Step-by-step explanation:
Answer:
-19.04 + 38.08 = 19.04
Select the expression equivalent to (5.2x + 4.8) − (-6x − 2)
A 11.2x + 6.8
B 11.2x - 2.8
C -0.8x + 6.8
D -0.8x - 2.8
Answers
100 points if someone gets it right
A rectangluar prism has volume of 2,610 cubic inches, length 3 inches, and width 29 inches . Find its height, in inches
Answers
Step-by-step explanation:
To find the height of the rectangular prism, you will need to use the formula for the volume of a rectangular prism, which is:
Volume = Length × Width × Height
In this problem, you have:
Volume = 2,610 cubic inches
Length = 3 inches
Width = 29 inches
You'll need to solve for Height. Using the formula:
2,610 = 3 × 29 × Height
First, multiply the length and width together:
2,610 = 87 × Height
Next, divide both sides by 87 to isolate Height:
Height = 2,610 / 87
Height = 30 inches
So, the height of the rectangular prism is 30 inches.
Answer:
30 inches.
Step-by-step explanation:
Given:
Volume=2610 cubic inches,
length=3 inches
width=29inches
Volume of a rectangular prism is given by.
Volume = length * width * height
We know the volume, length and width. So, we can find the height as follows:
Substituting value
2610=3*29*height
2610=87*height
height=2610/87
height=20 inches
Therefore, the height of the rectangular prism is 30 inches.
Ben helped his dad make soup. Their recipe made 15 cups. If they eat 2 cups, will their leftovers fit in a 64-ounce container.
Answers
Answer:
No, it would not fit because one cup is 8 ounces and if you times 8 and 13 it 104 so it would not fit they would need another container.
Step-by-step explanation:
hope it helps
if f is continuous for all real numbers dy/dx=f(x) and y(2)=4 then y(x)=
Answers
The general form of the solution is y(x) = ∫ f(x) dx + C If f is continuous for all real numbers dy/dx=f(x) and y(2)=4 then y(x)= 4.
I need to provide concise answers. However, I'll do my best to address your question while incorporating the mentioned terms. Given that f is continuous for all real numbers and dy/dx = f(x), we need to find the function y(x) given the initial condition y(2) = 4.
Since dy/dx = f(x), we can interpret this as a first-order differential equation, where the derivative of y(x) with respect to x is equal to the function f(x). To find y(x), we need to solve this differential equation and apply the initial condition provided.
To do this, we will integrate both sides of the equation with respect to x:
∫ dy = ∫ f(x) dx
y(x) = ∫ f(x) dx + C
where C is the constant of integration. Now, we can use the initial condition y(2) = 4 to determine the value of C:
4 = ∫ f(2) dx + C
Since we don't have an explicit expression for f(x), we cannot determine an exact formula for y(x) or the value of C. However, the general form of the solution to the given problem is:
y(x) = ∫ f(x) dx + C
with the initial condition y(2) = 4. To find the exact solution, we would need more information about the function f(x).
Learn more about real numbers here
https://brainly.com/question/17201233
#SPJ11
Find the measure of the indicated angle.

Answers
Answer:
Does the answer help you?

k-7/-0.4=85 show work pleasee!!!
Answers
Answer:
k=-27
Step-by-step explanation:
\(\frac{k-7}{-0.4}=85\\\\k-7=85(-0.4)\\\\k=7-34\\\\k=-27\)
John is saving to buy a new car that will cost him $24,000. John started his savings at the beginning of the school year and has been able to accumulate $1000 after the first month. John plans to continue his savings at a rate proportional to the amount he still needs to save. Determine John's savings amount as function of time Hint: A variable y is said to be proportional to a variable x if y=cx for some constant c.
Answers
John's savings amount as a function of time is S(t) = $24,000 / 25. Initially, he needs to save $24,000 for a new car. After the first month, he has saved $1,000. The savings amount is directly proportional to the time elapsed. The constant of proportionality is 1/24. Thus, John's savings amount can be determined based on the remaining amount he needs to save.
John's savings amount can be represented as a function of time and is proportional to the amount he still needs to save. Let's denote the amount John needs to save as N(t) at time t, and his savings amount as S(t) at time t. Initially, John needs to save $24,000, so we have N(0) = $24,000.
We know that John has saved $1,000 after the first month, which means S(1) = $1,000. Since his savings amount is proportional to the amount he still needs to save, we can write the proportionality as:
S(t) = k * N(t)
where k is a constant of proportionality.
We need to find the value of k to determine John's savings amount at any given time.
Using the initial values, we can substitute t = 0 and t = 1 into the equation above:
S(0) = k * N(0) => $1,000 = k * $24,000 => k = 1/24
Now we have the value of k, and we can write John's savings amount as a function of time:
S(t) = (1/24) * N(t)
Since John's savings amount is proportional to the amount he still needs to save, we can express the amount he still needs to save at time t as:
N(t) = $24,000 - S(t)
Substituting the expression for N(t) into the equation for S(t), we get:
S(t) = (1/24) * ($24,000 - S(t))
Simplifying the equation, we have:
24S(t) = $24,000 - S(t)
25S(t) = $24,000
S(t) = $24,000 / 25
Therefore, John's savings amount at any given time t is S(t) = $24,000 / 25.
To know more about proportional savings, refer here:
https://brainly.com/question/29251832#
#SPJ11
Alaina is giving a presentation about how the average college student spends their day. Through her research, she finds that most college students spend 30% of their day sleeping, 20% in class, 20% studying, and 30% socializing/participating in extracurricular activities. How should she graphically display this information in her presentation?
Answers
In her presentation, Alaina can use a pie chart to show information about how the typical college student spends their day.
A circular chart that has been divided into sectors or "pie slices" to represent numerical proportions is known as a pie chart. Each pie slice symbolises a percentage, and each slice's size is proportional to the percentage it represents.
In this instance, Alaina can separate the pie chart into four segments that stand in for the various activities that college students engage in throughout the day: sleeping, attending classes, studying, and participating in extracurricular activities. She can give each slice a unique colour and a label indicating the proportion it represents.
The pie chart, for instance, might have the following slices:
-30% of people are sleeping (blue).
- 20% of the class (in green)
20% of study time (coloured)
30% of time for socializing
Know more about pie chart here:
https://brainly.com/question/1109099
#SPJ11

What is 51.886 rounded to
Answers
answer:
it will be rounded to 52
Answer:
Not sure what you are wanting the number to be rounded to, so I'll just put all of the options here:
To the nearest whole number: 52
To the nearest tenth: 51.9
To the nearest one hundredth: 51.89
What is the slope of the line? x + 3 y = 10 x+3y=10x, plus, 3, y, equals, 10 Choose 1 answer: Choose 1 answer: (Choice A) A 1 3 3 1 start fraction, 1, divided by, 3, end fraction (Choice B) B 1 10 10 1 start fraction, 1, divided by, 10, end fraction (Choice C) C − 1 10 − 10 1 minus, start fraction, 1, divided by, 10, end fraction (Choice D) D − 1 3 − 3 1
Answers
Answer:
-1/3Step-by-step explanation:
The standard from of equation of a line written in slope-intercept format is expressed as y = mx+c where c is the slope of the line and c is the y-intercept.
Given the equation of the line x+3y = 10, to get the slope of the line, we need write he equation in standard from first by making y the subject of the formula as shown;
\(x+3y = 10\\\\subtract\ x \ from \ both \ sides\\\\x+3y-x = 10 -x\\\\3y = -x+10\\\\Divide \ through\ by \ 3\\\\\frac{3y}{3} = -\frac{x}{3} +\frac{10}{3} \\\\\)
\(y = -\frac{1}{3}(x) +\frac{10}{3} \\\)
Comparing the resulting equation with y = mx+c, the slope 'm' of the equation is -1/3
The slope of the line is -1/3.
the correct option is D.
To find the slope of the line given by the equation x + 3y = 10, we need to rewrite it in slope-intercept form, which is y = mx + b, where m represents the slope.
Let's rearrange the equation to solve for y:
x + 3y = 10
3y = -x + 10
y = (-1/3)x + 10/3
Comparing this equation to the slope-intercept form, we can see that the coefficient of x (-1/3) represents the slope.
Therefore, the slope of the line is -1/3.
Learn more about Slope here:
https://brainly.com/question/17158875
#SPJ6
Let X and Y be two independent random variables. Show that E[XY ] = E[X]E[Y ] provided that the expected values E[X] and E[Y ] exist. (You may assume that X and Y are either both discrete or both continuous; however, the results holds more general.)
Answers
The expected value of the product of two independent random variables X and Y is equal to the product of their individual expected values, given that the expected values of X and Y exist.
Let X and Y be two independent random variables. Then, the expected value of the product XY is given by:
E[XY] = ∫∫ xy fX(x) fY(y) dx dy
where fX(x) and fY(y) are the probability density functions of X and Y, respectively. Since X and Y are independent, their joint probability density function is given by:
fXY(x,y) = fX(x) fY(y)
Thus, the expected value of XY can be written as:
E[XY] = ∫∫ xy fX(x) fY(y) dx dy = ∫∫ xy fXY(x,y) dx dy
Now, we can use the linearity of expected value to split up the integral:
E[XY] = ∫∫ xy fXY(x,y) dx dy = ∫∫ x fX(x) y fY(y) dx dy
= (∫ x fX(x) dx) (∫ y fY(y) dy) = E[X] E[Y]
Therefore, we have shown that E[XY] = E[X] E[Y], given that X and Y are independent and that the expected values of X and Y exist.
Learn more about expected values here:
https://brainly.com/question/18523098
#SPJ11
