*HELP QUICK BEST FIRST PERSON WILL BE NAMED BRANLIEST*
Each cube inside the rectangular prism has an edge length of inch. What is the volume of
the rectangular prism?
256 in.
81 in
3 in
9 in.

Answers
Answer:
Step-by-step explanation:
length = 6 x 1/3 = 2 inches
width = 4 x 1/3 = 4/3 inches
height = 8 x 1/3 = 8/3 inches
volume = lwh = 2 x 4/3 x 8/3 = 64/9 cubic inches
Another approach is the following:
There are 6 x 4 x 8 = 192 cubes inside the prism,
Each cube has a volume of 1/27 cubic inches.
Therefore total volume = 192 x 1/27 = 192/27 = 9
Related Questions
Which equation represents the transformed function below

Answers
Olive has a plastic container shaped like a cube to put slime in. She measures one side and finds that it’s 0.5 foot long. Use the formula V = s3 to determine how many cubic feet of slime will fit in her container. PLEASE HELP!
Answers
Answer:
0.125 cubic feet
Step-by-step explanation:
Since the container has a shape of a cube with a measure of its side 0.5 ft, then;
Volume of the container, V = \(s^{2}\)
where s is the measure of its side.
s = 0.5 ft, then;
V = \((0.5)^{3}\)
= 0.125
V = 0.125 cubic feet
The cubic feet of slime that would fit in the container is 0.125.
Which is a unit rate?
15 miles per gallon
Answers
Step-by-step explanation:
Step:1
From given, the rate is
= 15 miles per gallon
= \frac{15}{1}115 = 15 miles.........................(1)
Step:2
Check for Option A,
= 30 miles per 3 gallons
= \frac{30}{3}330 = 10 miles.....................(2)
From the eqn (1) and (2),
Eqn (1) ≠ Eqn (2)
Step:3
Check for Option B and C are not match with given because, Miles provided first or top then the gallons provided the last or bottom.
Step:4
Check for Option D,
= 60 miles per 4 gallons
= \frac{60}{4}460 = 15 miles.........................(3)
From the eqn (1) and (3),
Eqn (1) ≠ Eqn (3)
Result:
The equivalent unit rate for 15 miles per gallon is 60 miles per 4 gallons (\frac{60 miles}{4 gallons}4gallons60miles ) .
i need help i’m confused

Answers
it’s x = 2 + BT
a number n is less than or equal to -7 or greater than 12
Answers
Answer:
Step-by-step explanation:
Work out percentage change to 2 decimal places when price of 97 is decreased to 90
Answers
Answer:
7.22?
Step-by-step explanation:
2.0 PLZZ help thank you

Answers
Answer: So if you do 50 dollars - 70% you get, 15 U.S. dollars
Hope this helps :)
Hope this help :)
x+y+z=12x+4y+2z = -6-x+9y-3z=-49 Can someone please help me solve this system of equation?
Answers
Let's begin by listing out the information given to us:
\(\begin{gathered} x+y+z=1 \\ 2x+4y+2z=-6 \\ -x+9y-3z=-49 \end{gathered}\)To solve this 3 variable equation, let's eliminate one of the variables
add equation 1 & 3, we have:
\(\begin{gathered} x-x+y+9y+z-3z=1-49 \\ 10y-2z=-48 \\ Make\text{ z the }subject,we\text{ have:} \\ -2z=-10y-48 \\ divide\text{ through by -2} \\ z=5y+24 \end{gathered}\)Substitute z into equation 1, 2 & 3
\(\begin{gathered} x+y+5y+24=1 \\ x+6y=1-24 \\ x+6y=-23 \end{gathered}\)\(\begin{gathered} 2x+4y+2\left(5y+24\right)=-6 \\ 2x+4y+10y+48=-6 \\ 2x+14y=-6-48 \\ 2x+14y=-54 \end{gathered}\)\(\begin{gathered} -x+9y-3\left(5y+24\right)=-49 \\ -x+9y-15y-72=-49 \\ -x-6y=-49+72 \\ -x-6y=23 \end{gathered}\)Solve as a simultaneous equation, we have:
\(\begin{gathered} x+6y=-23 \\ 2x+14y=-54 \\ \text{Multiply the top equation by 2 \& subtract it from the bottom equation} \\ 2\cdot(x+6y=-23)\Rightarrow2x+12y=-46 \\ 2x+14y=-54-(2x+12y=-46) \\ 2x-2x+14y-12y=-54-(-46) \\ 2y=-8 \\ y=-4 \end{gathered}\)Substitute y = -4 into x + 6y = -23, we have:
\(\begin{gathered} x+6\left(-4\right)=-23 \\ x-24=-23 \\ x=-23+24 \\ x=1 \end{gathered}\)Substitute y = -4 into z = 5y + 24, we have:
\(\begin{gathered} z=5\left(-4\right)+24 \\ z=-20+24 \\ z=4 \end{gathered}\)show your work
21 = −7n
Answers
Answer:
It would equal -3
Step-by-step explanation:
you are trying to find how to get a positive 21 so you would have to divide 21 by -7
21 ÷ -7 = -3
to make sure it's correct muiltply it
-7 × -3 = 21
So therefore n = -3
Which fraction is equivalent to a whole number?
Select all that apply.

Answers
Answer:
The answers are A B and C
they could be whole numbers
Step-by-step explanation:
need brainliest
Find the value of x.

Answers
Answer:
5
Step-by-step explanation:
Drag the prisms to the table in order from least volume to greatest volume.

Answers
Fourth prism, first prism, second prism and fourth prism is order from least volume to greatest.
What is Three dimensional shape?a three dimensional shape can be defined as a solid figure or an object or shape that has three dimensions—length, width, and height.
The volume of first prism with sides 2, 1.5 and 3.2
Volume=2×1.5×3.2
=9.6 in³
The volume of second prism with sides 1.5, 1.5 and 6
Volume=1.5×1.5×6
=13.5 in³
The volume of third prism with sides 2, 5/2 and 7/2
Volume=2×2.5×3.5
=17.5 in³
The volume of fourth prism with sides 1/2, 1/2 and 1/2
Volume=0.5×0.5×0.5
=0.125 in³
Hence fourth prism, first prism, second prism and fourth prism is order from least volume to greatest.
To learn more on Three dimensional figure click:
https://brainly.com/question/2400003
#SPJ1
The retirement age for NFL players follows a normal distribution with a mean of 33 years and a standard deviation of 2 years. A player gets injured and decided to retire at 28 years old. Approximately what percentage of NFL players retire at a younger age?
A) 0.62% B) 6.68% C) 13.35% D) 15.15% E) 19,77%
What age would an NFL player be if his retirement age was in the top 10% for all players? In other words, what age would he be if he played longer than 90% of all players?
A) 30.44 years old B) 31.2 years old C) 34.8 years old D) 35.56 years old E) 36.29 years old.
Answers
The percentage of NFL players retire at a younger age is A ) 0.62 % and the age is C ) 34.8 years .
Given :
The retirement age for NFL players follows a normal distribution with a mean of 33 years and a standard deviation of 2 years. A player gets injured and decided to retire at 28 years old.
percentage of NFL players retire at a younger age is :
P ( X < 28 ) = P ( x - μ / σ < 28 - 33 / 2 )
= P ( z < -5 / 2 )
= P ( z < -2.5 )
we know that at z score using calculator we can know the probability :
= 0.0062
= 0.0062 * 100%
= 0.62%
The age would he be if he played longer than 90% of all players is B ) 34.8 years old .
Learn more about the percentage here:
https://brainly.com/question/29116686
#SPJ4
Points A (4, 3), B (6, 4), C (5, 6) and D (3, 5) are the vertices of a square ABCD. The square ABCD is reflected about the line through (0, 0) and (-2, 2). Find the vertices of the image of the square ABCD and present both the figures on the same graph.
Answers
The vertices of the reflected square.
Let's calculate them:
A' = (-0.914, 3.914)
B' = (-2.828, 5.828)
C' = (-0.086, 7.086)
D' = (1.828, 5.172)
The vertices of the image of the square ABCD after reflecting it about the line through (0, 0) and (-2, 2), we can use the following steps:
Find the equation of the reflection line:
The reflection line passes through (0, 0) and (-2, 2).
We can calculate the slope (m) of the line using the formula (y2 - y1) / (x2 - x1):
m = (2 - 0) / (-2 - 0) = 2 / -2 = -1.
Using the point-slope form of a line (y - y1) = m(x - x1), we can use either of the given points to write the equation of the line:
y - 0 = -1(x - 0)
y = -x.
Find the midpoint of each side of the square:
The midpoints of the sides of a square are also the midpoints of its diagonals.
The midpoint of AB is ((4+6)/2, (3+4)/2) = (5, 3.5).
The midpoint of BC is ((6+5)/2, (4+6)/2) = (5.5, 5).
The midpoint of CD is ((5+3)/2, (6+5)/2) = (4, 5.5).
The midpoint of DA is ((3+4)/2, (5+3)/2) = (3.5, 4).
Reflect the midpoints about the line:
To reflect a point (x, y) about the line y = -x, we can find the perpendicular distance (d) from the point to the line and use it to determine the reflected point.
The perpendicular distance d from the line y = -x to a point (x, y) is given by the formula:
d = (y + x) / √(2).
The coordinates of the reflected points can be found using the formula for reflection across a line:
x' = x - 2d / √(2)
y' = y - 2d / √(2).
Calculate the reflected vertices:
The coordinates of the reflected vertices are as follows:
A' = (4 - 2(3.5 + 5) / √(2), 3 - 2(3.5 - 5) / √(2))
B' = (6 - 2(5 + 5) / √(2), 4 - 2(5 - 5) / √(2))
C' = (5 - 2(5.5 + 5) / √(2), 6 - 2(5.5 - 5) / √(2))
D' = (3 - 2(4 + 5) / √(2), 5 - 2(4 - 5) / √(2))
Now we can plot the original square ABCD and its image A'B'C'D' on the same graph to visualize the reflection.
For similar questions on vertices
https://brainly.com/question/1217219
#SPJ8
miko has 3.5 liters of water. how many bottles can fill if each bottle is to contain 0.25 liters of water?
Answers
Answer: 14 bottles
Step-by-step explanation:
To find out how many bottles Miko can fill with 3.5 liters of water, you can divide the total volume of water by the volume of each bottle:
number of bottles = total volume of water / volume of each bottle
Plugging in the given values, you get:
number of bottles = 3.5 L / 0.25 L
Performing the calculation gives you:
number of bottles = 14
So Miko can fill 14 bottles with 3.5 liters of water if each bottle holds 0.25 liters of water.
I hope this helps! Do you have any other questions?
Factor x4 - y4 completely.
A) (x^2 + y^2)(x + y)(x - y)
B) (x^2 - y^2)(x + y)(x - y)
C) (x^2 + y^2)(x - y)(x - y)
D) (x^2 + y^2)(x + y)(x + y)
Answers
Option A
Rate as BRAINLIEST
if any doubt leave a comment



What type of triangle is shown in the figure?
A
Equilateral
À
-y + 23
Obtuse
Right
B
C
Scalene
бу +2

Answers
Answer:
A equilateral
Step-by-step explanation:
hey, its equilateral because all sides of the triangle are the same length
what is the approximate length of segment PR?
25
11
125
18

Answers
Answer:
18
correct me if I'm wrong❌
find the inverse of each equation

Answers
The inverse of the equation is determined as \(y = \log_{6}(-3x)\).
option D is the correct answer.
What is the inverse of the equation?The inverse of the equation is calculated by applying the following method;
The given equation;
y = - 6ˣ/3
The inverse of the equation is calculated as;
multiply through by 3
\(-3x = 6^y\)
Take the logarithm of both sides of the equation with base -6:
\(\log_{6}(-3x) = y\)
Finally, replace y with x to obtain the inverse equation as follows;
\(y = \log_{6}(-3x)\)
Learn more about inverse of equation here: https://brainly.com/question/29390335
#SPJ1
write 5040 in scientific notation
Answers
5.04 × 10³
This is the scientific notation.
Answer:
5.04*10³
Step-by-step explanation:
5.04*10³
Find the x intercepts. Show all possible solutions.

Answers
For the function f(x) = 7/8x² - 14, the x-intercepts are x = -4 and x = 4.
What is a function?
In mathematics, a function is a unique arrangement of the inputs (also referred to as the domain) and their outputs (sometimes referred to as the codomain), where each input has exactly one output and the output can be linked to its input.
To find the x-intercepts of the function f(x), we need to solve the equation f(x) = 0.
f(x) = 7/8x² - 14
Substitute f(x) with 0 -
0 = 7/8x² - 14
Add 14 to both sides -
7/8x² = 14
Multiply both sides by 8/7 -
x² = 16
Take the square root of both sides -
x = ±4
Therefore, the x-intercepts of the function f(x) are x = -4 and x = 4.
To learn more about function from the given link
https://brainly.com/question/2284360
#SPJ1
Somebody can help me
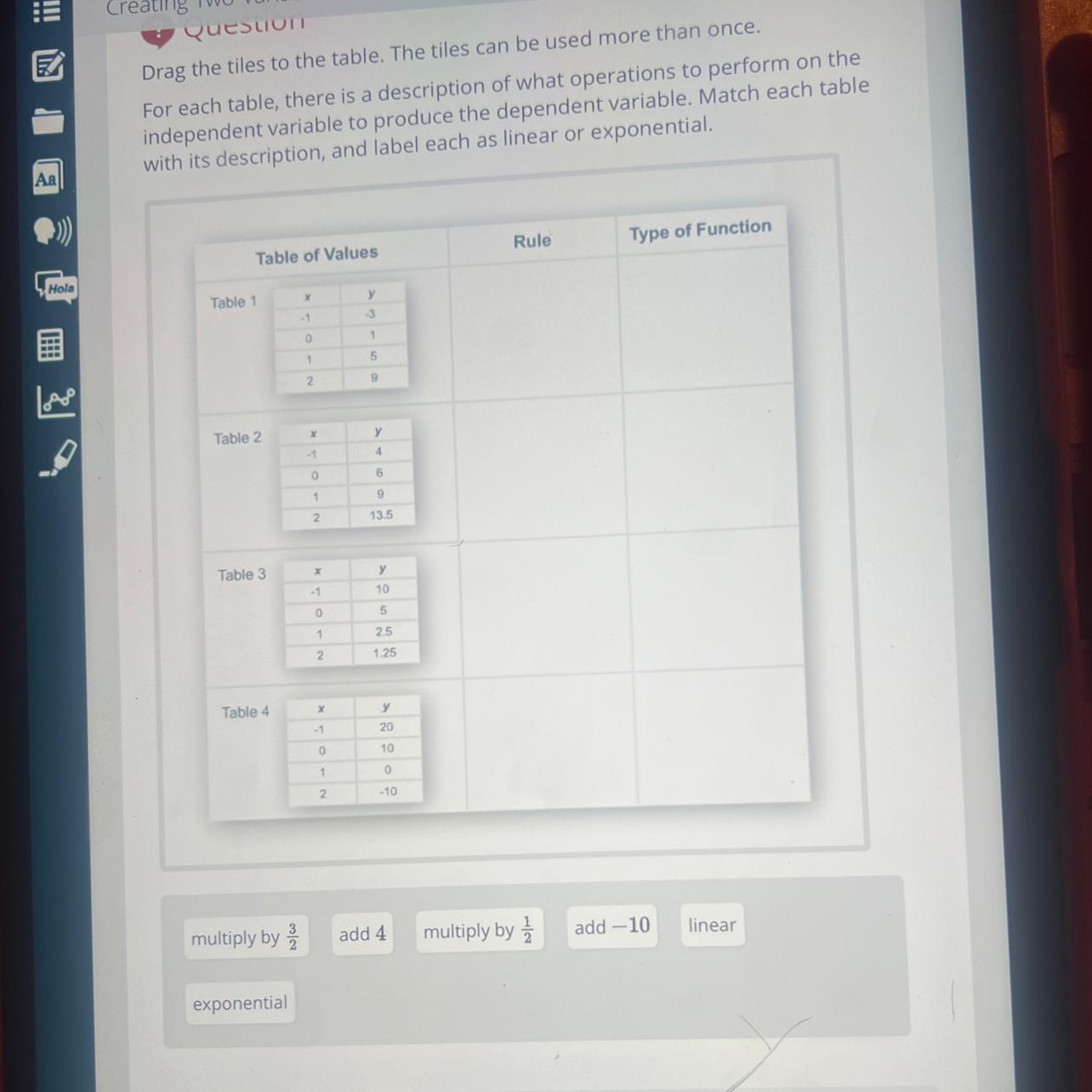
Answers
Answer:
Add 4 linear
Multiply by 3/2 exponential
Multiply by 1/2 exponential
Add -10 linear
Step-by-step explanation:
Look at what you need to do to the y value to get the next y value. Linear is when you add and exponential is when you multiply.
Which equation represents g(x)

Answers
Answer:
Option D. is the correct option
Step-by-step explanation:
The graph of g(x) is the translation of y = ∛x, which passes through origin (0, 0).
The graph in the figure is showing a shift of 1.5 units downwards.
Therefore, the new translated function g(x) will be represented by
g(x) = ∛x - 1.5
This graph can create a confusion of being shifted on x-axis but when we plug in the values of x in the options A and B, parent graph gets changed.
Therefore, option D. is the answer
The National Assessment of Educational Progress (NAEP) includes a mathematics test for eighth‑grade students. Scores on the test range from 0 to 500. Demonstrating the ability to use the mean to solve a problem is an example of the skills and knowledge associated with performance at the Basic level. An example of the knowledge and skills associated with the Proficient level is being able to read and interpret a stem‑and‑leaf plot.
In 2019, 147,400 eighth‑graders were in the NAEP sample for the mathematics test. The mean mathematics score was Xbar=282. We want to estimate the mean score in the population of all eighth‑graders. Consider the NAEP sample as an SRS from a Normal population with standard deviation =40.
If we take many samples, the sample mean Xbar varies from sample to sample according to a Normal distribution with mean equal to the unknown mean score in the population. What is the standard deviation of this sampling distribution?
Give your answer to four decimal places.
Answers
The standard deviation of the sampling distribution is approximately 0.3292.
What is central limit theorem?The behaviour of the sampling distribution of the mean is described by the central limit theorem, a key conclusion in statistics. It asserts that regardless of how the population distribution is shaped, if a random sample of size n is taken from a population with mean and standard deviation, the distribution of sample means will tend towards a normal distribution as n increases.
Because it enables us to utilise the normal distribution to draw conclusions about the population mean based on sample means, the central limit theorem has significant practical ramifications. Additionally, it offers a foundation for confidence interval estimation and statistical hypothesis testing.
The standard deviation is given by the formula:
SD = σ/√(n)
Now, substituting the value of σ = 40, n = 147,400 we have:
SD = σ/√(n) = 40/√(147400) ≈ 0.3292
Hence, the standard deviation of the sampling distribution is approximately 0.3292.
Learn more about central limit theorem here:
https://brainly.com/question/18403552
#SPJ1
I'm. not the best at finding angles sadly

Answers
Answer:
obtuse it is more than 90 so not a right and a straight angles is 180 degrees so it obtuse
What is the value of the digit in the ones place?
2,615
A. 50
B. 5
OC. 2,000
OD. 100
Answers
What is the expression for the area of a triangle with a height of 3x² units and a base of 6x² + 5x? The formula for area of the triangle is A = 1/2 b h
Answers
We have the formula for the area of the triangle as:
\(A=\frac{1}{2}\cdot b\cdot h\)If h and b are functions of x, we can replace them in the area function and have the area in function of x:
\(\begin{gathered} h=3x^2 \\ b=6x^2+5x \end{gathered}\)\(\begin{gathered} A=\frac{1}{2}\cdot b\cdot h \\ A=\frac{1}{2}(6x^2+5x)(3x^2) \\ A=\frac{1}{2}(18x^4+15x^3) \\ A=9x^4+\frac{15}{2}x^3 \end{gathered}\)Answer: A = 9*x^4 + (15/2)*x^3
The following are the ages of 12 history teachers In a school district 29,30,32,32,39,41,46,49,50,51,52,53 minimum lower quartile median upper quartile maximum and interquartile range
Answers
The five-number summary for this data set is 29, 32, 43.5, 50.5, and 53, and the interquartile range is 18.5.
How does interquartile range work?Measures of statistical dispersion, or the spread of the data, include the interquartile range. In addition to the IQR, other names for it include the midspread, middle 50%, fourth spread, and H-spread.
According to the given information:To find the five-number summary and interquartile range for this data set, we first need to find the quartiles.
Step 1: Find the median (Q2)
When a data collection is sorted from least to largest, the median is the midway value. Since there are 12 values in this data set, the median is the average of the sixth and seventh values:
Median (Q2) = (41 + 46)/2 = 43.5
Step 2: Find the lower quartile (Q1)
The lower quartile is the median of the lower half of the data set. Since there are 6 values below the median, we take the median of those values:
Q1 = (32 + 32)/2 = 32
Step 3: Find the upper quartile (Q3)
The upper quartile is the median of the upper half of the data set. Since there are 6 values above the median, we take the median of those values:
Q3 = (50 + 51)/2 = 50.5
Now we have all the information we need to construct the five-number summary and interquartile range:
Minimum: 29
Lower quartile (Q1): 32
Median (Q2): 43.5
Upper quartile (Q3): 50.5
Maximum: 53
Interquartile range (IQR) = Q3 - Q1 = 50.5 - 32 = 18.5
the five-number summary for this data set is 29, 32, 43.5, 50.5, and 53, and the interquartile range is 18.5.
To know more about interquartile range visit:
brainly.com/question/29204101
Given m || n, find the value of x and y.
(3y-17) (6x+20)°
(7x+13)
n

Answers
Answer:
Value of x = 7° & y = 45°
Step-by-step explanation:
According to the question m || n.
For x:
\( \rm \implies (7x + 13) \degree = (6x + 20) \degree \\ \\ \rm \implies 7x - 6x = 20 \degree - 13\degree \\ \\ \rm \implies x = 7 \degree\)
For y:
\( \rm \implies (3y - 17)\degree + (6x + 20) \degree = 180\degree \\ \\ \rm \implies (3y - 17)\degree + (6 \times 7 + 20)\degree = 180\degree \\ \\ \rm \implies (3y - 17)\degree + (42 + 20)\degree = 180\degree \\ \\ \rm \implies 3y - 17\degree + 62\degree = 180\degree \\ \\ \rm \implies 3y + 45\degree = 180\degree \\ \\ \rm \implies 3y = 180\degree - 45\degree \\ \\ \rm \implies 3y = 145\degree\\ \\ \rm \implies y = \bigg( \frac{145}{3} \bigg) ^\degree \\ \\ \rm \implies y = 45\degree\)
Given the table of candy distributions below, find P(Not green), the probability
of selecting anything but a green candy at random from a large bag.
Above or below is the list of possible answers

Answers
Answer:
C
Step-by-step explanation: