Give the equation of the graph of y = 2 cos 3x + 1 after it has been stretched vertically by a factor of 2, flipped upside down, and stretched horizontally by a factor of 2.
Answers
Answer:
Step-by-step explanation:
So we have the following chain of transformations
\(f(x)\to 2f(x)\to -2\f(x)\to -2f(\frac{1}{2}x)\\\)
So now
\(-2f(\frac{1}{2}x)=-2\left(2\cos(3x/2)+1\right)=-4\cos(3x/2)-2\)
Related Questions
Is it possible to solve 3 equations with 4 variables?
Answers
A linear system with 3 equations and 4 variables by representing it with an augmented matrix and bringing the matrix to reduced row-echelon form can be solved.
What is linear system?A mathematical representation of a system based on the application of a linear operator is known as a "linear system" in systems theory. Ordinarily, compared to nonlinear systems, linear systems display much simpler features and properties. The automatic control theory, signal processing, and telecommunications all heavily rely on linear systems as a mathematical abstraction or idealisation.
Linear systems, for instance, are frequently used to model the propagation medium for wireless communication systems. An operator, H, that converts an input, x(t), into an output, y(t), a kind of black box description, can be used to describe a general deterministic system.
The superposition principle, or alternatively both the additivity and homogeneity properties, must be satisfied by a system to be considered linear, and only then.
Learn more about linear system
https://brainly.com/question/28977228
#SPJ4
A gardener made a scale drawing of a lawn with a scale factor of 1:10. The
dimensions of her drawing are 7 inches long by 3 inches wide. Her partner plans
to make another scale drawing of the lawn, but with a scale factor of 1:2.
What are the dimensions of her scale drawing?
5 of 16 QUESTIONS
The length is 0.6 inch and the width is 1.4 inches.
The length is 15 inches and the width is 35 inches.
The length is 35 inches and the width is 15 inches.
The length is 1.4 inches and the width is 0.6 inch
SUB
Answers
Answer:
The length is 35 inches and the width is 15 inches.
Step-by-step explanation:
First work of the real length of the field. Given is the ratio of drawing to original and the dimensions of the drawing. so in real life the lawn measures 70 inches in length and 30 inches in width.
Now, we have to divide this in the ratio 1:2, which gives
The length of 35 inches and the width of 15 inches.
Hope this helps
Answer:
Your answer is 3 or C.. 35 inches and width of 15 :)
Step-by-step explanation:
The algebra question is in the image

Answers
Answer:
B
Step-by-step explanation:
A or constant is the answer
A piece of string is 120 centimeters long.
How long would the piece of string measure in meters?.
Answers
Answer:
1.2m
Step-by-step explanation:
1 meter = 100 cm
120cm * (1m/100cm) = 1.2m
when the length of a rectangle is increased by $20\%$ and the width increased by $10\%$, by what percent is the area increased?
Answers
Use formula to calculate area increase in rectangle when length and width increase by percentages, resulting in a 32% increase.
To find the percent by which the area of a rectangle increases when the length and width are increased by certain percentages, we can use the formula:
\(${Percent increase in area} = (\text{Percent increase in length} + \text{Percent increase in width}) + (\text{Percent increase in length} \times \text{Percent increase in width})$\)
In this case, the percent increase in length is 20% and the percent increase in width is 10\%. Plugging these values into the formula, we get:
\($\text{Percent increase in area} = (20\% + 10\%) + (20\% \times 10\%)$\)
\($\text{Percent increase in area} = 30\% + 2\%$\)
\($\text{Percent increase in area} = 32\%$\)
Therefore, the area of the rectangle increases by 32%.
To know more about area of rectangle Visit:
https://brainly.com/question/8663941
#SPJ11
hi i am stuck on this word problem and need help
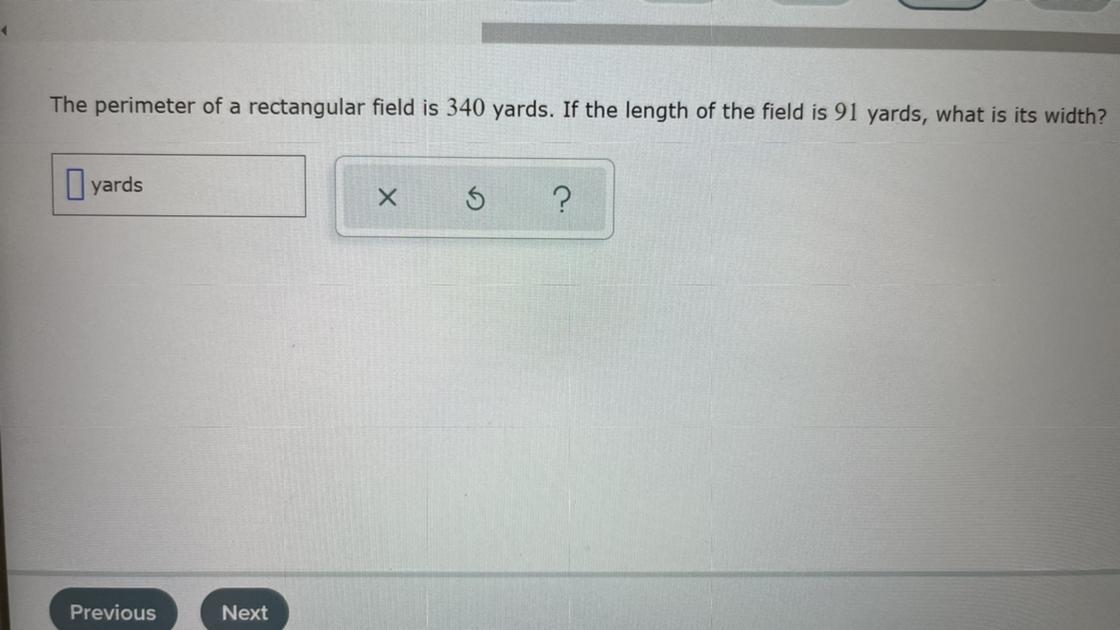
Answers
Solution
Given that the Perimeter is: 340 yards. Lenght is 91 yards
Since P = 2(L + W)
where L is the Length
W is the width
=> 340 = 2(91 + W)
=> 340 = 182 + 2W
=> 158 = 2W
Dividing both sides by 2
=> W = 79
Hence, the width is 79 yards
Answer: it would be 79yards
Step-by-step explanation: 91•2=182
340-182=158
158/2=79yards
for a standard normal distribution, 95% of the datapoints are contained in the interval [ -x , x ]. what is the value of x?
Answers
Standard deviation - The value of x is 1.96.
What is standard normal distribution?
A continuous probability distribution for a real-valued random variable in statistics is known as a normal distribution or Gaussian distribution.
As given, for a standard normal distribution, 95% of the data points are contained in the interval [ -x , x ].
The standard normal distribution, commonly known as the z-distribution, is a unique type of normal distribution in which the mean and standard deviation are both equal to 1. By transforming its values into z-scores, any normal distribution can be standardised. Z-scores indicate how far away from the mean each number is from.
Hence, from the standard normal table, the value of x = 1.96 for 95% confidence level.
To know more about the standard deviation, click on the link
https://brainly.com/question/26822684
#SPJ4
Help w number 1 please super confused

Answers
An equilateral triangle is one that has all three of its sides be in line with one another.A slash mark is used to indicate the congruent sides.Congruent angles are ∠L and ∠X, ∠G and ∠Y, and ∠F and ∠T.
How do you identify congruent angles?An equilateral triangle is one that has all three of its sides be in line with one another.A slash mark is used to indicate the congruent sides.An equilateral triangle always has angles that are 60° in length.
It is referred to as an isosceles triangle when a triangle's two sides are identical. When the corresponding sides and angles of two angles match, the angles are said to be congruent.
When stacked, two angles are also congruent if they match.
If they line up with each other after turning or moving it, then.
Also creating equivalent vertex angles are a parallelogram's diagonals.
Congruent sides - L and X, G and Y, and F and T.
Congruent angles - ∠L and ∠X, ∠G and ∠Y, and ∠F and ∠T.
ΔLGF ≅ ΔXYT
Congruent angles are ∠L and ∠X, ∠G and ∠Y, and ∠F and ∠T.
Congruent sides are L and X, G and Y, and F and T.
To learn moire about congruent angles refer
https://brainly.com/question/11949261
#SPJ1
Please help middle school math

Answers
9514 1404 393
Answer:
3 < b-a < 7
Step-by-step explanation:
The maximum difference will occur when the smallest 'a' value is subtracted from the largest 'b' value:
9 -2 = 7
The minimum difference will occur when the largest 'a' value is subtracted from the smallest 'b' value:
7 -4 = 3
So, the possible range of values of b-a is ...
3 < b-a < 7
What two nonnegative real numbers with a sum of have the largest possible product?.
Answers
The two non negative real numbers with a sum of 60 that have the largest possible product are 30 and 30.
What are non negative numbers?
Non-negative numbers are those that are either zero or positive (remember that 0 and 0 are the same). An integer that is either positive or zero is considered a non-negative integer. It is the result of adding all the natural numbers together with zero. It can be defined as the set "0, 1, 2, 3,...," and is also known as Z.
An integer that is either positive or zero is considered a non-negative integer.
Let us assume the two non negative numbers are \(x\) and \(y\).
According to the question,
Sum of two non negative numbers = 60
⇒ \(x+y=60\)
⇒ \(y=60-x\)
Their product will be given as,
⇒ \(P=xy\)
⇒ \(P=x(60-x)\)
⇒ \(P=60x-x^2\)
For the product to be largest \(P'(x)=0\)
⇒ \(P'(x) = 60-2x\)
⇒ \(60-2x=0\)
⇒ \(2x=60\)
⇒ \(x=30\)
Now, for the value of \(y\)
⇒ \(y=60-x\)
⇒ \(y=60-30\)
⇒ \(y=30\)
Therefore, the two non negative numbers are 30, 30.
To know more about the non negative numbers..........
https://brainly.com/question/19578996
#SPJ4
what’s the difference between the area of the larger circle and the area of the smaller circle? in pi

Answers
Answer:
105 pi m^2
Step-by-step explanation:
radius squared - radius squared =
(16+3)^2 - 16^2 =
19^2 - 16^2 =
361-256= 105
1. What is the next number in the pattern below?
0, 5, 11, 18, _____
can someone pls help me with this? Thank you!
Answers
0 to 5 = +5
5 to 11 = +6
11 to 18 = +7
18 to ? = +8
? = 26
Helppppp I neeeed it!!!!!!

Answers
Ht + 16t -80t -384 = 0
So, yes the rocket hits the ground.
If we use the limit comparison test to determine, then the series Σ 1 n=17+8nln(n) 1 converges 2 limit comparison test is inconclusive, one must use another test. 3 diverges st neither converges nor diverges
Answers
The series \($\displaystyle \sum _{ n=17}^{\infty }\dfrac{ 8n\ln( n)}{ n+1}$\) cannot be determined by the limit comparison test and requires another test for convergence.
The limit comparison test is inconclusive in this case. The limit comparison test is typically used to determine the convergence or divergence of a series by comparing it to a known series. However, in this case, it is not possible to find a known series that can be used for comparison. The series \($\displaystyle \sum _{ n=17}^{\infty }\dfrac{ 8n\ln( n)}{ n+1}$\) does not have a clear pattern or a simple known series to compare it with. Therefore, the limit comparison test cannot provide a definitive conclusion.
To determine the convergence or divergence of the series \($\displaystyle \sum _{ n=17}^{\infty }\dfrac{ 8n\ln( n)}{ n+1}$\), one must employ another convergence test. There are several convergence tests available, such as the integral test, ratio test, or root test, which can be applied to this series to determine its convergence or divergence. It is necessary to explore alternative methods to establish the convergence or divergence of this series since the limit comparison test does not yield a conclusive result.
To learn more about convergence refer:
https://brainly.com/question/30275628
#SPJ11
The tetrahedron enclosed by the coordinate planes and the plane 2x + y + z =4
Answers
volume= 16/3, A coordinate plane is a graphing and description system for points and lines. A vertical (y) axis and a horizontal (x) axis make up the coordinate plane. There are four quadrants in the coordinate plane. The point where these lines connect is called the origin (0, 0).
limits
z= 0 to z = 4-y-2x
y= 0 to y = 4- 2x
x= 0 to x= 2
volume
v= \(\int\limits^2_0 \int\limits^4_0 \int\limits^4_0 dzdydx\)
v= \(\int\limits^2_0 \int\limits^4_0 (4-y-2x) dydx\)
v= \(\int\limits^2_0 ( 4y- y^{2} / 2 - 2xy) ^4^-^2^x _0\)
dx= \(\int\limits^2_0 [ 16-8x - 16+ 4x^2 - 16x / 2 - 8x+ 4x^2 ] dx\)
v= \(\int\limits^2_0 [ 8+ 2x^2- 8x] dx\\\)
= [ 8x + 2x^3 / 3 - 8x^2 / 2 ] ^2_0
= [16+ 16/3- 16]
v= 16/3
Learn more about coordinate planes from brainly, visit: brainly.com/question/13611766
#SPJ4
Complete Question
Question: Sketch The Tetrahedron Enclosed By The Coordinate Planes And The Plane 2x+Y+Z=4. Use A Triple Integral To Find The Volume Of The tetrahedron
find the area of the surface generated when the given curve is revolved about the given axis. y=16x-7, for 3/4
Answers
The calculation involves finding the definite integral of 2πy√\((1 + (dy/dx)^2)\) dx over the interval [0, 3/4].
To find the surface area generated when the curve y = 16x - 7 is revolved about the y-axis over the interval [0, 3/4], we can use the formula for the surface area of revolution. The formula is given by:
A = 2π ∫[a,b] y √(1 + (dy/dx)^2) dx
In this case, we need to find the definite integral of y √(\(1 + (dy/dx)^2\)) with respect to x over the interval [0, 3/4].
First, let's find dy/dx by taking the derivative of y = 16x - 7:
dy/dx = 16
Next, we substitute y = 16x - 7 and dy/dx = 16 into the surface area formula:
A = 2π ∫[0, 3/4] (16x - 7) √(1 + 16^2) dx
Simplifying the expression inside the integral:
A = 2π ∫[0, 3/4] (16x - 7) √257 dx
Now, we can evaluate the integral to find the surface area. Integrating (16x - 7) √257 with respect to x over the interval [0, 3/4] will give us the exact numerical value of the surface area.
learn more about definite integral here:
https://brainly.com/question/30760284
#SPJ11
the process of using sample statistics to draw conclusions about population parameters is called: group of answer choices calculating the confidence level. calculating descriptive statistics. finding the significance level. doing inferential statistics.
Answers
Option D. Doing inferential statistics. Inferential statistics is the process of using sample statistics to draw conclusions about population parameters.
This involves making inferences about a population based on data collected from a sample, and using statistical methods to estimate the true values of population parameters, such as the mean or proportion.
Descriptive statistics, on the other hand, involves summarizing and describing the characteristics of a sample or population, without making any inferences about the larger population.
Calculating the confidence level and finding the significance level are important components of inferential statistics, as they help to assess the accuracy and reliability of the estimates made based on the sample data. However, these are not the primary processes involved in using sample statistics to draw conclusions about population parameters.
To learn more about Inferential statistics please click on below link.
https://brainly.com/question/30574113
#SPJ4
The process of using sample statistics to draw conclusions about population parameters is called: group of answer choices
A. Calculating the confidence level.
B. Calculating descriptive statistics.
C. Finding the significance level.
D. Doing inferential statistics.
What are the unknown angles?

Answers
Answer:
x = 28°
y= 62°
Step-by-step explanation:
Trigonometry ratios:To find x, we can use the ratio Tan.
\(\sf Tan \ x = \dfrac{opposite \ side \ of \ x^\circ}{adjacent \ side \ of \ x^\circ}\\\\\)
\(\sf = \dfrac{7}{13}\\\\= 0.5385\)
\(\sf x = tan^{-1} \ (0.5385)\\\\x = 28.30^\circ\\\\x = 28^\circ\)
x + y + 90 = 180 {Angle sum property of triangle}\\
28 + y + 90 = 180
y + 118 = 180
y = 180 - 118
y = 62°
Part 3 of 5 (c) n=4, p=0.21, X=3 P(X) = _______
Answers
The value of P(X = 3) is 0.02923.
To find P(X) for the given values n = 4, p = 0.21, and X = 3, we can use the probability mass function (PMF) of the binomial distribution.
The PMF of the binomial distribution is given by:
P(X) = \(C_X^n * p^X * (1 - p)^{(n - X)\)
where C (n, X) is the binomial coefficient, given by n! / (X! * (n - X)!), representing the number of ways to choose X successes out of n trials.
Substituting the values into the formula, we have:
P(X = 3) = (C (4, 3) * (0.21)³ * (1 - 0.21)⁽⁴⁻³⁾
Calculating the binomial coefficient:
(C(4, 3)) = 4! / (3! * (4 - 3)!) = 4
Substituting the values into the formula:
P(X = 3) = 4 * (0.21³) * (0.79¹)
Calculating the result:
P(X = 3) = 4 * 0.009261 * 0.79
P(X = 3) ≈ 0.02923
Therefore, P(X = 3) is approximately 0.02923.
Learn more about binomial distribution here
https://brainly.com/question/29137961
#SPJ4
Use the following image to answer the question:
Flowchart with 3 boxes. The first one is empty, the second one has State Appellate Court, and the third one has State Supreme Court.
Which of the following labels completes the chart? (3 points)
a
U.S. Circuit Courts of Appeals
b
State Trial Court
c
U.S. District Court
d
State Court of Appeals
Answers
Answer:
the answer is the state trial.
Step-by-step explanation:
Answer:
US Circuit Courts of Appeals
Step-by-step explanation:
The lowest courts are circuit courts. They are the courts of original jurisdiction. The 24 Illinois Circuit Courts can hear almost all cases. The intermediate courts are the appellate courts. There are five appellate districts. The court of last resort is the Supreme Court. The Illinois Supreme Court can hear cases directly from a circuit or an appellate court in the state.
Find the length of the missing side of the right triangle. Round to three decimal places, if necessary. 1) a -10, b 24 Solve the problem. If necessary, round to the nearest tenth.
Answers
Answer: We can use the Pythagorean theorem to solve this problem, which states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
In this case, we have:
a = -10
b = 24
c = ?
Using the Pythagorean theorem, we can solve for c:
c^2 = a^2 + b^2
c^2 = (-10)^2 + 24^2
c^2 = 676
c = sqrt(676)
c = 26
Therefore, the length of the missing side of the right triangle is 26 units.
The length of the missing side of the right triangle is 26. To find the length of the missing side of a right triangle, we can use the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b).
The formula is:
\(c² = a² + b²\)
In this problem, a = 10 and b = 24. To find the length of the missing side (the hypotenuse, c), we can plug these values into the formula:
c² = 10² + 24²
c² = 100 + 576
c² = 676
Now, we take the square root of both sides to find the length of the missing side:
c = √676
c = 26
So, the length of the missing side (the hypotenuse) of the right triangle is 26.
Learn more about triangle here:
https://brainly.com/question/2773823
#SPJ11
Samuel opened a savings account and deposited $1,500.00. The account earns 1% interest, compounded annually. If he wants to use the money for senior prom in 3 years, how much money will he have to spend on his outfit and limo?
Answers
Answer:
uhm chile sooooo anywayzz
Step-by-step explanation:
Which of the following expressions is equivalent to (10n - 8) - (4n + 3) Explain why you choose the answer. SHOW ALL STEPS:
A. 6n - 11
B. 6n + 5
C. 14n + 5
Answers
Answer: A. 6n-11
Step-by-step explanation:
First, ignore the parenthesis because it is addition and subtraction so they are commutative. 10n-4n = 6n and -8-3 is the same as -8+-3 which is -11. Combining the answer gives 6n-11.
1. Correct to the nearest millimetre, the length of a side of a regular hexagon is 3.6 cm. Calculate the upper bound for the perimeter of the regular hexagon.
2. Kelly runs a distance of 100 metres in a time of 10.52 seconds.
The distance of 100 metres was measured to the nearest metre.
The time of 10.52 seconds was measured to the nearest hundredth of a second.
(d) Calculate the lower bound for Kelly’s average speed. Write down all the figures on your calculator display.
3. Steve measured the length and the width of a rectangle.
He measured the length to be 645 mm correct to the nearest 5 mm.
He measured the width to be 400 mm correct to the nearest 5 mm.
Calculate the lower bound for the area of this rectangle.
Give your answer correct to 3 significant figures.
4. The length of the rectangle is 35 cm correct to the nearest cm.
The width of the rectangle is 26 cm correct to the nearest cm.
Calculate the upper bound for the area of the rectangle.
Write down all the figures on your calculator display.
Answers
1. The upper bound for the perimeter of the regular hexagon is 21.9 cm.
2. All figures on the calculator display for the calculation of Kelly's average speed is: 99.5 / 10.51 = 9.46717412
3. the lower bound for the area of the rectangle is 2.55 × 10⁵ mm²
4. Upper bound for area = 937.6525 cm²
How to calculate the perimeter of the hexagon1. The upper bound for the perimeter of the regular hexagon can be calculated by multiplying the length of one side by 6 (the number of sides in a hexagon):
Upper bound for perimeter = 6 × (3.6 + 0.05) = 21.9 cm (rounded to one decimal place)
2. Kelly's average speed can be calculated by dividing the distance she ran by the time she took:
Average speed = distance / time
The lower bound for the distance is 99.5 m (since 100 m was measured to the nearest meter, the actual distance could be as low as 99.5 m).
The lower bound for the time is 10.51 s (since 10.52 s was measured to the nearest hundredth of a second, the actual time could be as low as 10.51 s).
Therefore, the lower bound for Kelly's average speed is:
Average speed = 99.5 / 10.51 = 9.4617 m/s (rounded to 4 decimal places)
3. The length of the rectangle is 645 mm correct to the nearest 5 mm, which means it could be as small as 642.5 mm or as large as 647.5 mm. We can express this as:
645 mm ± 2.5 mm, similarly
400 mm ± 2.5 mm
Lower bound for length = 645 - 2.5 = 642.5 mm
Lower bound for width = 400 - 2.5 = 397.5 mm
Lower bound for area = 642.5 × 397.5 = 255393.75 mm²
Rounded to 3 significant figures, the lower bound for the area of the rectangle is 2.55 × 10⁵ mm².
4. To calculate the upper bound for the area of the rectangle, we need to multiply the upper bounds for the length and width of the rectangle:
Upper bound for length = 35 + 0.45 = 35.45 cm
Upper bound for width = 26 + 0.45 = 26.45 cm
Upper bound for area = 35.45 × 26.45 = 937.6525 cm²
Learn more about upper bound at:
https://brainly.com/question/28725724
#SPJ1
SEE PICTURE FOR QUESTION

Answers
how do u solve this inequality

Answers
Answer/explanation:
Multiply to remove the fraction, then set equal to 0 and solve.
Inequality Form:
m≥−98
Interval Notation:
[−98,∞)
hope this helps
You can infer causality from a correlational result, but only when the r value is greater than ?A. 0B. 5C. 1
Answers
You can infer causality from a correlational result, but only when the r value is greater than:
C. 1
Causality refers to a situation in which one event causes another. When there is a correlation between two variables, it means that they tend to move in the same direction.
However, this does not necessarily mean that one event causes the other. In order for a correlation to indicate causality, the correlation coefficient (r) must be greater than 1. If the correlation coefficient is below 1, then there is not enough evidence to suggest that one event causes the other.
In addition, there are other factors that need to be considered when assessing causality from a correlational result.
For example, the strength of the relationship between the variables, the direction of the relationship, and the consistency of the results over time. It is also important to consider the context in which the research was conducted, as this may have an effect on the results.
Learn more about causality:
brainly.com/question/9369134
#SPJ4
Here are two expressions whose sum is a new expression, A.
(2x²+5)+(6x0-7)=A
Select all the values that we can put in the box so that A is a polynomial.
Answers
All the values that we can put in the given box so that A is a polynomial,
\(A=(2x^{2} +5-7)\\A =2(x^{2} -1)\\A=2(x+1) (x-1)\)
\(x\) can take any value except ±1.
To learn more, https://brainly.com/question/20121808
#SPJ4
Line segment RS has endpoints R(–2, 4) and S(–4, –1).
Line segment R''S'' has endpoints R''(3, –3) and S''(5, 2).
Name the rigid transformations that map line segment RS to line segment R''S''.
A- reflection over the line y = x, followed by a translation (x, y) → (x + 1, y + 1)
B- rotation of 180° about the origin, followed by a translation (x, y) → (x + 1, y + 1)
C- rotation of 90° counterclockwise about the origin, followed by a translation (x, y) → (x + 2, y + 1)
D- translation (x, y) → (x + 1, y + 1), followed by a rotation of 180° counterclockwise about the origin
Answers
The rigid transformations that map line segment RS to line segment R''S'' is rotation of 180° about the origin, followed by the translation (x,y)→(x+1,y+1).
A 180-degree rotation about the origin will alter both X's and Y's signs to the opposite, thus if one of them is negative, the other will be positive, and vice versa.
Point R being (-2,4), the first transformation would include changing the signs to make it (2,-4) and the second transformation would involve adding 1 to both of them:
(x,y) →(x+1,y+1)
(2,-4)→(2+1,-4+1)
(2,4)→(3,-3)
Similarly we will do with point S(-4,-1) which results in S''(5,2).
Hence, the answer.
To learn more about rigid transformations here:
https://brainly.com/question/1761538
#SPJ1
Evaluate the expression for b = 3 and c = 5.
b2c − 11 =
Answers
Answer:
34Step-by-step explanation:
b = 3 and c = 5Substitute and evaluate:
b²c - 11 =3²*5 - 11 = 9*5 - 11 =45 - 11 =34Answer:
\(b = 3 \ \: \: : c = 5 \\ \\ b {}^{2} c - 11 = \\ \\ \\ {3}^{2} \times 5 - 11 = \\ \\ 9 \times 5 - 11 = \\ \\ 45 - 11 = \\ \\ = 34\)