find the number shows 5 by 7 is 125
Answers
Answer:
answer is 175
Step-by-step explanation:
Let the number be x,
x*5/7=125
multiply 125 by 7 because if divide is there when it will go to another side it will be multiply so,
x*5=125*7
or,x*5=875
now you should do divide by 5 because multiply will be divide when it will go to another side
x=875/5
x=175
Hope it is helpful for you
if it is mark me brainest and follow me
Related Questions
What is an equation of the line that passes through the points (0, -7) and (-8, 3)?
Answers
Answer (assuming it can be in slope-intercept form):
\(y = -\frac{5}{4} x-7\)
Step-by-step explanation:
1) First, find the slope of the line by using the slope formula, \(m = \frac{y_2-y_1}{x_2-x_1}\). Substitute the x and y values of the given points into the formula and solve:
\(m = \frac{(3)-(-7)}{(-8)-(0)}\\m = \frac{3+7}{-8-0} \\m = \frac{10}{-8} \\m = -\frac{5}{4}\)
So, the slope is \(-\frac{5}{4}\).
2) Now, use the point-slope formula \(y-y_1 = m (x-x_1)\) to write the equation of the line in point-slope form. Substitute real values for the \(m\), \(x_1\), and \(y_1\) in the formula.
Since \(m\) represents the slope, substitute \(-\frac{5}{4}\) in its place. Since \(x_1\) and \(y_1\) represent the x and y values of one point the line intersects, choose any one of the given points (either one is fine, it will equal the same thing at the end) and substitute its x and y values into the formula as well. (I chose (0, -7), as seen below.) Then, isolate y to put the equation in slope-intercept form and find the following answer:
\(y-(-7) = -\frac{5}{4} (x-(0))\\y + 7 = -\frac{5}{4} x\\y = -\frac{5}{4} x-7\)
expand and simplify (2x+5)(3x+1`)
Answers
Answer:
6x^2 + 17x + 5
Step-by-step explanation:
(2x + 5)(3x + 1)
= 6x^2 + 2x + 15x + 5
= 6x^2 + 17x + 5
The expression (2x+5)(3x+1) is a product of two binomials. To expand this product, we multiply each term in the first binomial by each term in the second binomial, using the distributive property of multiplication.
When we multiply 2x by 3x, we get 6x^2.
Then we multiply 2x by 1, which gives us 2x.
Next, we multiply 5 by 3x, which gives us 15x.
Finally, we multiply 5 by 1, which gives us 5.
Putting these terms together gives us the expanded form of the expression:
(2x+5)(3x+1) = 6x^2 + 2x + 15x + 5
Simplifying, we can add the 2x and 15x terms to get 17x, giving us the final simplified expression:
(2x+5)(3x+1) = 6x^2 + 17x + 5.
Before beginning voice lessons, Aubrey already knew how to sing 357 pieces, and she expects to learn 2 new pieces during each week of lessons. After 78 weeks of voice lessons, how many pieces will Aubrey be able to sing, in total? Write and solve an equation to find the answer. pieces
Answers
Please help! i did question A and B already I just need help with C PLEASE I hope you can see the questions! Thank you lots

Answers
Step-by-step explanation:
Here is how I would work this one out :
Treat the first 4 deposits as an annuity due...calculate the value at the end of the year , then calculate that amount compounded quarterly for 39 more years:
Annuity due: FV = A [ ( (1+i)^n -1) / i ] (1 +i) ] where i = .015/4 = .0125
n = 4 ( one year)
and a = 450
plug in the numbers to find FV = $ 1856.96 at the end of year one.
then use this 'deposit ' compounded quarterly for 39 more years (n = 156)
$ 1856.96 ( 1 + .0125)^156 = $ 12895.17
A measuring instrument is used to obtain n determinations X
1
,⋯,X
n
of a physical constant μ>0. Suppose that the measuring instrument is known to be positively biased such that it "over-measures" μ, on average, by 0.1 units. Assume that the errors ε
1
,⋯,ε
n
are otherwise independent and identically distributed normal RVs with known variance σ
2
>0. a. State the constant-mean model for X
i
, for i=1,⋯,n, including the common distribution G
ε
(e) of ε
1
,⋯,ε
n
. Completely specify the common distribution of X
1
,⋯,X
n
, including the parameter and parameter space; that is, specify the model F analogously to F
2
in Example 2 of Lecture 1 Is model F identifiable? Prove, if yes, or disprove, otherwise. HINT: Use Problem #1 above. I suggest you use the contrapositive condition in the definition of identifiability in Lecture 1 to prove identifiability of F. Suppose the amount of positive bias is unknown, denoted by β>0. Is model F identifiable? Prove, if yes, or disprove, otherwise.
Answers
The model F is identifiable, and the true value of μ can be estimated from the observed measurements X1, X2, ..., Xn.
To formulate the constant-mean model for the determinations X1, X2, ..., Xn, we can start by considering the individual measurements and their relationship to the true value of the physical constant μ.
Let's denote the true value of the physical constant as μ. The measurements X1, X2, ..., Xn are biased and overestimate μ on average by 0.1 units. This means that each measurement can be modeled as:
Xi = μ + εi + 0.1
where Xi is the i-th measurement, εi represents the measurement error, and 0.1 represents the bias.
The measurement errors ε1, ε2, ..., εn are assumed to be independent and identically distributed (i.i.d.) normal random variables with variance σ².
Therefore, we can specify the common distribution Gε for the measurement errors as:
Gε ~ N(0, σ²)
Now, let's determine the distribution of the measurements X1, X2, ..., Xn. Using the constant-mean model, we can express each measurement Xi in terms of the true value μ, the measurement error εi, and the bias term 0.1.
Xi = μ + εi + 0.1
The measurements X1, X2, ..., Xn are also assumed to be independent and identically distributed (i.i.d.) random variables.
Therefore, the common distribution F for the measurements can be specified as:
F ~ N(μ + 0.1, σ²)
Here, the parameter of interest is μ, the true value of the physical constant. The parameter space for μ depends on the specific context and constraints of the problem.
Identifiability refers to the property of being able to uniquely determine the parameters of a statistical model from the observed data.
In this case, model F is identifiable because the true value of the physical constant μ can be estimated by subtracting the known bias of 0.1 from the observed measurements. Even if the bias term β (unknown positive bias) is included, it can be absorbed into the estimation of μ as long as it remains constant across all measurements.
Therefore, model F is identifiable, and the true value of μ can be estimated from the observed measurements X1, X2, ..., Xn.
Learn more about random variables here:
https://brainly.com/question/14356285
#SPJ11
(5.06).
A recent Internet survey showed per-day lodging expenses at Disney World in Orlando range from less than $100 for a campsite to more than $2,000 for a top luxury room. The cost-per-day
average of the top 10 most popular hotels at Disney World is $348.
If the standard deviation is $80, find the z-score for a per-day expense of $400.
If the data are approximately normally distributed with mean $348 and standard deviation $80, what percent of the hotels have per-day expenses greater than $2687
Submit
Previous
ces, show both decimal places
Next
Answers
On solving the provided question, we can say that equation is z = x-u/p => z = 300-348/80 = 0.65, The z score for a per - day expense of $400 is 0.65
What is equation?A mathematical equation is a formula that joins two statements and uses the equal symbol (=) to indicate equality. A mathematical statement that establishes the equality of two mathematical expressions is known as an equation in algebra. For instance, in the equation 3x + 5 = 14, the equal sign places the variables 3x + 5 and 14 apart. The relationship between the two sentences on either side of a letter is described by a mathematical formula. Often, there is only one variable, which also serves as the symbol. for instance, 2x – 4 = 2.
The z score for a $400 per day charge is 0.65, but around 84.13% of hotels cost more than $268.
The z score is used to calculate how many standard deviations above or below the mean the raw score is. Giving the z score are:
equation is
z = x-u/p
u = mean, x = raw score, p standard deviation
z = 300-348/80 = 0.65
The z score for a per - day expense of $400 is 0.65
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
Which rectangle is similar to a rectangle with length of 12 yards and 23 yards?
a rectangle with length 14 yards and 13 yards
a rectangle with length 14 yards and 25 yards
a rectangle with length 2 yards and 3 yards
a rectangle with length 212 yards and 223 yards
Answers
Answer:
a rectangle with 2 yards and 3 yards
Step-by-step explanation:
12 yards and 23 yards
x and 2x - 1
------------------------------------
2 and 3 = x and 2x - 1
2 and 2(2) - 1 = 2 and 3
I might be wrong.
PLEASE HELP ME
I really need this answer

Answers
Answer:
x≤6
Step-by-step explanation:

Answer: x<6
Step-by-step explanation:
closed circle line going left from 6
Find the probability of getting a doublet in a throw of a pair of dice.
Answers
These are the outcomes (1,1),(2,2),(3,3),(4,4,)(5,5) and (6,6).
To find the total number of outcomes, note that there are 6 choices for the first die (values 1–6) and there are 6 choices for the second die (again values 1–6) and so by the Multiplication Principle (MP) there are 36 total outcomes from rolling two dice once.
Now we have the following:
P(getting a doublet) =
Total number of outcomes
Number of ways to get double
=
36
6
=
6
1
Thus, the probability of getting a doublet is
6
1
.
Question:
Find the probability of getting a doublet in a throw of a pair of dice.
Answer:
The probability is 1 out of 6.
Explanation:
There are a total of 6 possibilities that you get a doublet, which is {1, 1}, {2, 2}, {3, 3}, {4, 4}, {5, 5}, and {6, 6}.
The total possibilities of throwing a dice are 6 possibilities for the first dice, and 6 possibilities for the second dice. Which results in a total of 6 × 6 = 36 possibilities available.
Probability = Possibilities of getting doublet ÷ Total possibilities = 6 ÷ 36 = 1 ÷ 6.
Hopefully this answer will help you.
Maya brought some orange slices for her volleyball team to eat between games. They
divided the orange slices equally among the 8 team members, so each team member got
6 orange slices. Lets be the number of orange slices Maya brought. Write and solve an
equation to find s.
Answers
Answer:
48
Step-by-step explanation:
6 times 8=48
Tell whether the relationship shown in the mapping diagram is a function or not.

Answers
Answer:
It is a function
Step-by-step explanation:
The x-values do not repeat so it is a function.
.On a sequence diagram, a message represents a service requestTrue or false?
Answers
On a sequence diagram, a message does represent a service request. A sequence diagram is a type of interaction diagram in Unified Modeling Language (UML) .So the answer to your Question is True.
UML illustrates the interactions between objects or components within a system over a specific period of time. It visualizes the flow of messages between objects to depict the order of and the timing of these interactions. In a sequence diagram, messages are used to represent communication between objects. Messages can be synchronous, where the sender waits for a response before proceeding, or asynchronous, where the sender does not wait for a response. In the context of a service-oriented architecture, a message can represent a service request being sent from one object or component to another. By using messages to represent service requests, sequence diagrams provide a clear and visual representation of the interactions and flow of information within a system. They help in understanding the sequence of steps involved in a process and the dependencies between different components or objects.
Learn more about Unified Modeling Language (UML) here:
https://brainly.com/question/30504439
#SPJ11
PLEASE HELP!!
Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.
Based on the figure on the graph, match the described transformations with the transformed figures.
reflected across the x-axis
rotated 180° clockwise
translated 9 units to the
right and 2 units down
reflected across the y-axis



Answers
The transformation of the given image follows the pattern; Reflection across the x-axis, then translation by 2 units downwards, the reflection across the y-axis.
How to carry out transformation reflection?
From the given first image, we see that it is in the first quadrant but by the second image, we see that it is now mirrored along the horizontal axis. Thus, we can say that it is reflected across the x-axis.
After reflection, across the x-axis, we see that it was translated down by 2 units.
The last transformation is that we see it is now in quadrant 3 which means it was now reflected across the y-axis.
The transformation of the given image follows the pattern; Reflection across the x-axis, then translation by 2 units downwards, the reflection across the y-axis.
Read more about Transformation Reflection at; https://brainly.com/question/4289712
#SPJ1
Which expression is equivalent to the following complex fraction? StartFraction 2 Over x EndFraction minus StartFraction 4 Over y EndFraction divided by StartFraction negative 5 Over y EndFraction + StartFraction 3 Over x EndFraction StartFraction 3 y + 5 x Over 2 (y minus 2 x) EndFraction StartFraction 2 (y minus 2 x) Over 3 y minus 5 x EndFraction StartFraction 2 (y minus 2 x) (3 y minus 5 x) Over x squared y squared EndFraction StartFraction x squared y squared Over 2 (y minus 2 x) (3 y minus 5 x) EndFraction
Answers
The equivalent expression of \(\frac{\frac 2x - \frac 4y}{-\frac 5y + \frac 3x}\) is \(\frac {2(y - 2x)}{ 3y-5x}\)
How to determine the equivalent expression?The complete question is in the attached image
We have:
\(\frac{\frac 2x - \frac 4y}{-\frac 5y + \frac 3x}\)
Take the LCM
\(\frac{\frac {2y - 4x}{xy}}{\frac{-5x + 3y}{xy}}\)
Divide through by xy
\(\frac {2y - 4x}{-5x + 3y}\)
Rewrite as:
\(\frac {2y - 4x}{ 3y-5x}\)
Factor out 2
\(\frac {2(y - 2x)}{ 3y-5x}\)
Hence, the equivalent expression of \(\frac{\frac 2x - \frac 4y}{-\frac 5y + \frac 3x}\) is \(\frac {2(y - 2x)}{ 3y-5x}\)
Read more about equivalent expression at:
https://brainly.com/question/24734894
#SPJ1

10. A box contains five and two-thirds cups of rice. If three fourths of the rice will
be used, how many cups of rice remained in the box?
14
D.
Answers
Therefore, after using three-fourths of the rice in the box, 4 and 1/4 cups of rice remained.
To find the number of cups of rice that remained in the box, we need to calculate three-fourths (3/4) of the total amount of rice in the box.
The total amount of rice in the box is given as five and two-thirds cups. To work with a fraction, we can convert the mixed number to an improper fraction:
5 and 2/3 = (5 * 3 + 2) / 3 = 17/3 cups
Now, we can find three-fourths (3/4) of 17/3:
(3/4) * (17/3) = (3 * 17) / (4 * 3) = 51/12 = 4 and 3/12 = 4 and 1/4 cups
Therefore, after using three-fourths of the rice in the box, 4 and 1/4 cups of rice remained.
Learn more about three-fourths here
https://brainly.com/question/16953584
#SPJ11
Please answer this question now in two minutes

Answers
Answer:
LJ = CB
Therefore, CJ is 50km
Hellllp please problem above

Answers
Angle(x)=42 degrees
Arc(WV)=2*Angle(x)
Arc(WV)=2*42°=84°
What is the measure of
PLEASE HELP HURRY
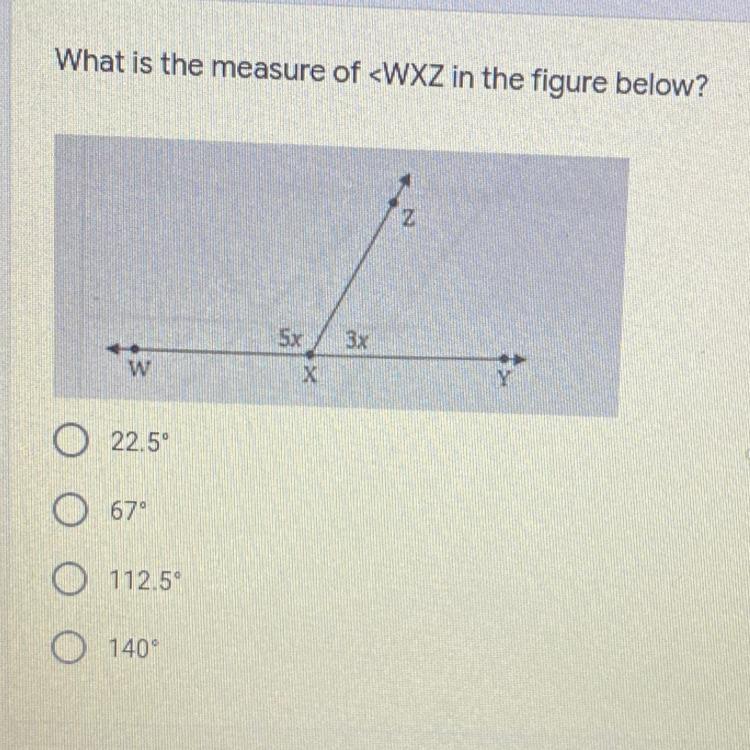
Answers
Answer:
112.5°
in pretty sure that's the answer
Eli's house is due west of Yardley and due south of Salem. Yardley is 7 miles from Eli's house and 9 miles from Salem. How far is Salem from Eli's house, measured in a straight line? If necessary, round to the nearest tenth
Answers
By Pythagorean , Eli's home is thus roughly **11.4 miles** from Salem when viewed from a straight line.
Define Pythagorean theorem?A fundamental relationship between a right triangle's three sides in Euclidean geometry is known as the Pythagorean theorem. The hypotenuse is the side that forms the right angle, and the rule says that the square of its length is equal to the sum of the squares of the lengths of the other two sides. In other words, if the hypotenuse is length c and the legs of a right triangle are lengths a and b, then a²+ b² = c² .
Call Yardley Y, Salem S, and Eli's home E. As far as we are aware, Y is located 7 miles from E and 9 miles from S.
We can check that the distance between Eli's house and Salem is the hypotenuse of a right triangle with Yardley as one of the vertices because Eli's house is located due west of Yardley and due south of Salem. The Pythagorean theorem can be used to determine this distance.
Eli's home is 11.4 miles from Salem at a distance of√(7 + 9 ) = √(130).
√(130) = 11.4miles
Eli's home is thus roughly **11.4 miles** from Salem when viewed from a straight line.
To know more about Pythagorean theorem visit:
brainly.com/question/14930619
#SPJ1
Describe the end behavior of a 9th degree polynomial with a negative leading coefficient??
Answers
Answer:
Up left, down right
Step-by-step explanation:
First, polynomials with odd degrees will have end behaviors in two different directions.
Since the leading coefficient is negative, the end behavior will be up left and down right.
So, the end behavior is up left, down right.
The end behavior of a 9th-degree polynomial with negative leading coefficients is up left, downright.
We have to determine
The end behavior of a 9th-degree polynomial with a negative leading coefficient??
What is a negative leading coefficient?If the leading coefficient is negative and the exponent of the leading term is even, the graph falls to the left and right.
What is the equation of 9th-degree polynomial?
The equation of the 9th-degree polynomial is;
\(\rm x^9+3x^8+4x^7+x^6+x^5+9x^3+2x^2+x+1=0\)
The degree of the polynomial is 9 which is odd.
Hence, the end behavior of a 9th-degree polynomial with negative leading coefficients is up left, downright.
To know more about Polynomial click the link given below.
https://brainly.com/question/17822016
* Ono 3 b) P and are the subsets of universal set U. If n (p) = 55% n (Q) = 50% and n(PUO)complement = 15% find: (i) n(PUQ) (ii) n(PDQ) (iii)n(only P) iv. n(only Q).
Answers
The probability of the sets are solved and
a) n(P U Q) = 85%
b) n(P ∩ Q) = 20%
c) n(only P) = 35%
d) n(only Q) = 30%
Given data ,
P and are the subsets of universal set U
And , n (p) = 55% n (Q) = 50% and n(PUO)complement = 15%
Now , we'll use the formula for the union and intersection of sets:
n(P U Q) = n(P) + n(Q) - n(P ∩ Q)
n(P ∩ Q) = n(P) + n(Q) - n(P U Q)
n(only P) = n(P) - n(P ∩ Q)
n(only Q) = n(Q) - n(P ∩ Q)
We're given that:
n(P) = 55%
n(Q) = 50%
n(P U Q)' = 15%
To find n(P U Q), we'll use the complement rule:
n(P U Q) = 100% - n(P U Q)'
n(P U Q) = 100% - 15%
n(P U Q) = 85%
Now we can substitute the values into the formulas above:
(i)
n(P U Q) = n(P) + n(Q) - n(P ∩ Q)
n(P ∩ Q) = n(P) + n(Q) - n(P U Q)
n(P ∩ Q) = 55% + 50% - 85%
n(P ∩ Q) = 20%
(ii)
n(P ∩ Q) = 20%
(iii) n(only P) = n(P) - n(P ∩ Q)
n(only P) = 55% - 20%
n(only P) = 35%
(iv)
n(only Q) = n(Q) - n(P ∩ Q)
n(only Q) = 50% - 20%
n(only Q) = 30%
Hence , the probability is solved
To learn more about probability click :
https://brainly.com/question/17089724
#SPJ1
Consider a LOS transmitting antenna with a height of 75 m.
a. Calculate the maximum distance between the transmitting
antenna and the receiving antenna if the receiving antenna is at
ground level.
b.
Answers
a. The maximum distance between the transmitting antenna and the receiving antenna, when the receiving antenna is at ground level, is approximately 30,955 meters.
b. The maximum distance between the transmitting antenna and the receiving antenna, when the receiving antenna height is increased to 50 m, is still approximately 30,955 meters.
a. To calculate the maximum distance between the transmitting antenna and the receiving antenna when the receiving antenna is at ground level (height = 0), we can use the formula for the horizon distance:
d = √((2 * h * R) + h^2)
where:
d is the maximum distance between the antennas,
h is the height of the transmitting antenna, and
R is the radius of the Earth.
Height of the transmitting antenna, h = 75 m
Height of the receiving antenna, h = 0 m
Radius of the Earth, R ≈ 6,371,000 meters
Substituting the values into the formula:
d = √((2 * 75 * 6,371,000) + 75^2)
d ≈ √((957,150,000) + 5,625)
d ≈ √(957,155,625)
d ≈ 30,955 meters (approximately)
Therefore, the maximum distance between the transmitting antenna and the receiving antenna, when the receiving antenna is at ground level, is approximately 30,955 meters.
b. Now, if the height of the receiving antenna is increased to 50 m, we can calculate the new maximum distance using the same formula.
Height of the transmitting antenna, h = 75 m
Height of the receiving antenna, h = 50 m
Radius of the Earth, R ≈ 6,371,000 meters
Substituting the values into the formula:
d = √((2 * 75 * 6,371,000) + 75^2)
d ≈ √((957,150,000) + 5,625)
d ≈ √(957,155,625)
d ≈ 30,955 meters (approximately)
Therefore, the maximum distance between the transmitting antenna and the receiving antenna, when the receiving antenna height is increased to 50 m, is still approximately 30,955 meters. The height of the receiving antenna does not affect the maximum distance in a LOS scenario.
Your question is incomplete but most probably your full question was
Consider A LOS Transmitting Antenna With A Height Of 75 M.
A. Calculate The Maximum Distance Between The Transmitting Antenna And The Receiving Antenna If The Receiving Antenna Is At Ground Level.
B. If Now, The Receiving Antenna Height Is Increased To 50 M, Calculate The Maximum Distance Possible For LOS Transmission.
Learn more about transmitters here
brainly.com/question/13721041
#SPJ11
how do sociologists know if the sample they are using is representative? a. if the sample has an even number, decided by the researcher, of people from several different categories or backgrounds
Answers
If the sample has the same mix of people, in the same proportions, as the population being studied then sociologists know if the sample they are using is representative. So the option c is correct.
No subject is off-limits when sociologists use the sociological lens and start asking questions. Every facet of human behaviour has the potential to be studied. Sociologists cast doubt on the society that people have built and inhabit. They observe behavioral patterns as individuals navigate that world.
Sociologists have uncovered workplace patterns that have revolutionized industries, family patterns that have educated parents, and educational patterns that have supported structural changes in classrooms by using sociological methodologies, methodical research, and a scholarly interpretive approach.
To learn more about Sociology link is here
brainly.com/question/25099331
#SPJ4
The complete question is;
How do sociologists know if the sample they are using is representative?
a. If the people in the sample freely volunteered to serve as representatives
b. If the sample has an even number, decided by the researcher, of people from several different categories or backgrounds
c. If the sample has the same mix of people, in the same proportions, as the population being studied
d. If the participants have been interviewed to reveal possible bias.
Part C
Calculate the ratio of AB to BC and the ratio of AD to DC. Round your answers to the
hundredths place. What do you notice about the ratios?
B 0 g = 1,
Font Sizes
A
= = = =
How would i calculate the ratios in geomatry like this would ask me its also asking the ratios lengths if someone could explain this thatd be great
Answers
Let us first draw the diagram given to understand the given information in the problem: The diagram above shows a quadrilateral ABCD, and point E is on segment AB. We are required to find the ratio of AB to BC and the ratio of AD to DC. To calculate the ratios in geometry:
Calculation of Ratio of AB to BC
In ΔABC, AB and BC are the sides that we want to find the ratio of. We can use the following formula to calculate the ratio of AB to BC:
Ratio of AB to BC = AB / BC
Using the diagram, we can see that AB = 7
and BC = 6. Substituting these values in the formula above, we get:
Ratio of AB to BC = AB / BC
= 7 / 6 = 1.1667
Rounding to the hundredths place, we get:
Ratio of AB to BC = 1.17
Calculation of Ratio of AD to DC
In ΔADC, AD and DC are the sides that we want to find the ratio of. We can use the following formula to calculate the ratio of AD to DC:
Ratio of AD to DC = AD / DC
Using the diagram, we can see that AD = 7
and DC = 11. Substituting these values in the formula above, we get:
Ratio of AD to DC = AD / DC
= 7 / 11 = 0.6364
Rounding to the hundredths place, we get:
Ratio of AD to DC = 0.64
Notice that the ratio of AB to BC is greater than 1, while the ratio of AD to DC is less than 1. Also, the sum of these ratios is greater than 1 (1.17 + 0.64 = 1.81). These observations indicate that the quadrilateral ABCD is not a parallelogram.
To know more about parallelogram visit:
brainly.com/question/28854514
#SPJ11
Two lines, A and B, are represented by the following equations: Line A: y = -x + 4 Line B: y = -x + 4 Which statement is true about the solution to the set of equations? (4 points) There is one solution at (1, 2). There are infinitely many solutions. There is one solution at (1, 5). There is no solution.
Answers
MANY SOLUTIONS
If you eliminate the x's you have 4 left so both 4 are equal to each other and so it is many solutions because if you have two variable or numbers equal to each other it is many solutions
-x+4=-x+4
+x. +x
4=4
Write 10.71⎯⎯
as a mixed number in simplest form.
Answers
Which recurrence relation describes a function that has the same asymptotic growth as , defined by the recurrence relation: Group of answer choices
Answers
The recurrence relation that describes a function with the same asymptotic growth as f(n), defined by the recurrence relation, is f(n) = f(n-1) + g(n), where g(n) is any function that grows slower than or at the same rate as f(n).
In this recurrence relation, f(n) represents the function being described, f(n-1) represents the previous term in the sequence, and g(n) represents the additional term being added at each step.
By choosing a g(n) that grows slower than or at the same rate as f(n), we ensure that the additional term does not significantly affect the overall growth of the function.
This results in both f(n) and the given recurrence relation having the same asymptotic growth.
It is important to note that the exact form of g(n) is not specified in the question, so there are multiple possible answers that would satisfy the condition of having the same asymptotic growth.
To know more about function visit;
brainly.com/question/30721594
#SPJ11
What does Grothendieck mean by "One should never try to prove anything that is not almost obvious"?
Answers
Which of the following ordered pairs is a solution to the inequality y is greater than one fourth times x plus 5? (12, 8) (11, 7) (8, 6) (4, 7)
Answers
The ordered pair that is a solution to the inequality:
y > (1/4)*x + 5
is (4, 7)
Which of the given ordered pairs is a solution for the inequality?Here we have the inequality:
y > (1/4)*x + 5
To check if an ordered pair is a solution, we just need to replace the values of the ordered pair on the inequality and see if it is true.
For example, for (12, 8)
We will get:
8 > (1/4)*12 + 5
8 > 3 + 5
8 > 8
This is false, so (12, 8) is not a solution.
The pair that is a solution is:
(4, 7)
7 > (1/4)*4 + 5
7 > 1 + 5
7 > 6
This is true.
Learn more about inequalities:
https://brainly.com/question/24372553
#SPJ1
Hello hello :))) please help me with this problem

Answers
=> 12 in = 30.48cm
4 in = 10.16cm
14 in = 35.56cm
Since both of the figures are cylinders, we have to find them one by one
Find the volume of the upper cylinder
Formula: V = pi*r^2*h
We know, pi = 3,
radius = diameter of base/2
=> r = 30.48cm/2 = 15.24cm
height = 30.48cm
We get V=3*(15.24)^2*30.48=21237.6cm^3
Find the volume of lower cylinder
Formula: V = pi*r^2*h
We know, pi = 3,
radius = diameter of base/2
=> r = 35.56cm/2 = 17.78cm
height = 10.16cm
We get
V = 3*(17.78)^2*10.16 = 9635.6cm^3
Therefore, the volume of the object is
V = 21237.6cm^3 + 9635.6cm^3
= 30873.2cm^3.