Find a formula for the inverse of the given function. f(x) = 3x
Answers
Related Questions
Median of 5,8,11,8,3,2,4,6,9,8
Answers
Answer:
8
Step-by-step explanation:
is the median
give email id
2,3,4,5,6,8,8,8,9,11
Then get the middle numbers which are 6 and 8 then add it and devide by 2
6+8/2=14/2
=7
I hope this was helpful pls mark answer as brainest answer if it was the best
Pls have a nice day
kiran's Mother gets a resturant bill for $40. She has a coupon for 25% off. After the discount is applied, she adds 20% as a tip. What is the total after the discount and tip? Explain or show your reasoning.
Answers
Answer: $36
Step-by-step explanation:
Bill is $40, the 25% off coupon is used, and the 20% tip is left.
Step 1: Find 25% of 40
is/40=25/100 ------> 40(25)/100=10
Step 2: Find the new bill price after discount
40-10=30
Step 3: Find the 20% tip of 30
is/30=20/100 ---------> 30(20)/100=6
Step 4: Add the tip with the restaurant bill
30+6=$36
How do i solve this?

Answers
9514 1404 393
Answer:
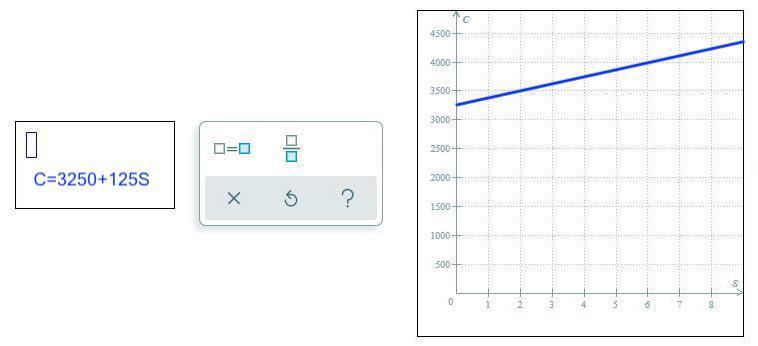
see the attachment
Step-by-step explanation:
The cost when no sugar is transported is 3250, so that is the "y-intercept". (There is no "y". The vertical axis is labeled "c", so that is the c-intercept.)
The cost per ton is 125, so that is the slope or "rate of change". Each increase of 1 unit in the value of "s" will result in an increase of 125 in the value of "c". The grid lines for "c" are 500 apart, so 1 vertical grid space will correspond to 500/125 = 4 horizontal grid spaces.
The graph starts at the left side halfway between 3000 and 3500. It goes up 1 grid square for each 4 grid squares to the right.
A teacher has a large container filled with blue, red, and green beads. She wants her students to estimate the proportion of red beads. Each student shakes the container, selects 50 beads, counts the number of red beads, and returns the beads to the container. One student’s sample contained 19 red beads. The students are asked to construct a 95% confidence interval for the true proportion of red beads in the container. Are the conditions for inference met?
Yes, the conditions for inference are met.
No, the 10% condition is not met.
No, the randomness condition is not met.
No, the Large Counts Condition is not met.
Answers
Answer:
A
Step-by-step explanation:
Answer:
C: No, the randomness condition is not met.
Step-by-step explanation:
took the test on edge
James and Theo are need 2 but don’t need 2
Answers
find the value \((-38)x^{2}\)
Answers
You are doing a walkathon/runathon to raise money for your school. You can walk at a rate of 4 miles per hour and run at a rate of 6 miles per hour. You need to cover more than 8 miles in order to raise your part of the money. Which of the following linear inequalities can be used to determine how long you must walk (w) and run (r) in order to cover more than 8 miles? O 4w + 6r > 8 4w + 65 = 8 O 4w + 6r > 8 O 4w + 6r

Answers
We need to determine which of the given inequalities can be used to determine how long you must walk (w) and run (r) in order to cover more than 8 miles.
We know that you can walk at a rate of 4 mi/h, and run at a rate of 6mi/h.
Thus, if you walk for w hours, you will walk a distance d₁, in miles, given by:
\(d_1=4w\)Also, if you run r hours, you will run a distance d₂, in miles, given by:
\(d_2=6r\)Now, notice that the total distance is the sum of d₁ and d₂. And the total distance, in miles, must be greater than 8.
We represent 'greater than' using the symbol '>':
\(\begin{gathered} d_1+d_2>8 \\ \\ 4w+6r>8 \end{gathered}\)Therefore, the correct option is:
\(4w+6r>8\)1frogaroni please answer this 888888,1*9000.
Answers
Answer:
Hello here is the answer hope this helps 79999992900.
Step-by-step explanation:
THE SEVEN APPLEWOMEN
Seven apple women, possessing respectively 20, 40, 60, 80, 100, 120, and 140
apples, went to market and sold all their apples at the same price, and each
received the same sum of money. What was the price?
Answers
Answer:
The amount each took home was 20 unit currency.
Step-by-step explanation:
The given parameters are
The number of apples with each of the seven apple women = 20, 40, 80, 100, 120, and 140
The number of apples each woman has can be written in the following formula obtained online which is a series formula
a·n + (n - 1), (a + b)·n + (n - 2), (a + 2·b)·n + (n - 3), (a + 3·b)·n + (n - 4), (a + 4·b)·n + (n - 5), (a + 5·b)·n + (n - 6), (a + 6·b)·n + (n - 7)
Which gives;
a·n + (n - 1) = 20
(a + b)·n + (n - 2)=40
(a + 2·b)·n + (n - 3) = 60
(a + 3·b)·n + (n - 4) = 80
(a + 4·b)·n + (n - 5) = 100
(a + 5·b)·n + (n - 6) = 120
(a + 6·b)·n + (n - 7) = 140
Solving the above system, we get
n = 7, a = 2, b = 3
Which gives
2×7 + 6 = 20
5×7 + 5=40
8×7 + 4 = 60
11×7 + 3 = 80
14×7 + 2 = 100
17×7 + 1 = 120
20×7 + 0 = 140
Whereby all the women sold the apples for the same sum price, based on market pricing if groups of apples are sold at 1 unit currency for 7, and extras are sold for 3 unit currency per extra 1, we have the amount taking home by each of them given as follows;
2×1 + 6×3 = 20
5×1 + 5×3=20
8×1 + 4×3 = 20
11×1 + 3×3 = 20
14×1 + 2×3 = 20
17×1 + 1×3 = 20
20×1 = 20
Therefore, the amount each took home was 20 unit currency.
WILL GIVE BRAINLIEST AND THANKS. determine if these are tangent to the circle

Answers
Answer:
19 Five is not tangent to the circle.
20 Eight is tangent to the circle.
Step-by-step explanation:
In order for one of the legs to be a tangent to a circle, the length must be part of a right angle triple.
I don't think the diagram on the left is, but I'll check it.
5^2 + 12^2 =
25 + 144 =
169
square root of 169 is 13
The length of the hypotenuse should be 13 not 14. Fourteen does not make Pythagorean triple. 13 would. So the line 5 units long does not make a tangent to the given circle.
The diagram on the right is a different story. 6 8 and 10 do make a Pythagorean triple, even though the two diagrams are not the same.
The radius and the distance to the external point form a right angle.
The Pythagorean triple is
6^2 + 8^2 = 10^2
36 + 64 = 100
100 = 100
help meeeeeeeeeeeeeee pleaseee

Answers
The table of solutions for the given equation (y = -2x²) include the following:
x y_
-2 -8
-1 -2
0 -0
1 -2
2 -8
Also, a graph of the solution of this equation (y = -2x²) has been plotted in the image attached below.
How to determine the solution?In order to determine the valid and true solutions to the given quadratic equation, we would have to substitute the values of contained in the table into the quadratic equations as follows;
At x = -2, the value of point y is as follows:
y = -2x²
y = -2(-2)²
y = -2 × 4
y = -8
At x = -1, the value of point y is as follows:
y = -2x²
y = -2(-1)²
y = -2 × 1
y = -2
At x = 0, the value of point y is as follows:
y = -2x²
y = -2(0)²
y = -2 × 0
y = 0
At x = 1, the value of point y is as follows:
y = -2x²
y = -2(1)²
y = -2 × 1
y = -2
At x = 2, the value of point y is as follows:
y = -2x²
y = -2(2)²
y = -2 × 4
y = -8
In conclusion, we can logically deduce that the graph of this quadratic equation forms a downward parabola.
Read more on graphs here: brainly.com/question/4546414
#SPJ1

Help please!!!!!!! this is due tomorrow

Answers
Answer:
(4,0) (0,2)
(2,0) (0,4)
(3,0) (0,-2)
(-1.5, 0) (0,3)
Step-by-step explanation:
First:
2x + 4y = 8
Let y = 0
2x = 8 Divide both sides by 2
x = 4
(4,0)
2x + 4y = 8
Let x = 0
4y = 8 Divide both sides by 4
y = 2
(0,2)
Second
6x + 3y = 12
Let y = 0
6x = 12 Divide both sides by 2
x = 2
(2,0)
6x + 3y = 12
Let x = 0
3y = 12 Divide both sides by 2
y = 4
(0,4)
Third
See from the graph that the the line is crossing the x axis at the point (3,0) and the y axis at (0,-2)
Fourth
See from the graph that the line is crossing the x axis at (-1.5,0) and the y axis at (0,3)
agnetic field b = 1 t goes out of the plane of the page. a straight wire carries a current 1 a from right to left. find the direction of force acting on the wire. A) out of the page
B) into the page
C) left, in the plane of the page
D) right, in the plane of the page
E) up, in the plane of the page
Answers
According to the right-hand rule for the force on a current-carrying wire in a magnetic field, the direction of the force is perpendicular to both the direction of the current and the direction of the magnetic field.
The direction of the force acting on the wire can be determined using the right-hand rule for the force on a current-carrying wire in a magnetic field. According to the right-hand rule:
Point the fingers of your right hand in the direction of the current (from right to left).
Curl your fingers towards the direction of the magnetic field (out of the page).
Your thumb will now point in the direction of the force.
Therefore, the direction of the force on the wire will be upwards, perpendicular to both the current and the magnetic field.
Since the force is perpendicular to the plane of the page, the answer would be (E) up, in the plane of the page.
To know more about right-hand rule visit:
https://brainly.com/question/9750730
#SPJ11
Change the word phrase to an algebraic expression. Use x to represent the number. The product of 9 and two more than a number
Answers
The algebraic expression for "The product of 9 and two more than a number" is 9(x + 2).
In the given word phrase, "a number" is represented by the variable x. The phrase "two more than a number" can be translated as x + 2 since we add 2 to the number x. The phrase "the product of 9 and two more than a number" indicates that we need to multiply 9 by the value obtained from x + 2. Therefore, the algebraic expression for this word phrase is 9(x + 2).
"A number": This is represented by the variable x, which can take any value.
"Two more than a number": This means adding 2 to the number represented by x. So, we have x + 2.
"The product of 9 and two more than a number": This indicates that we need to multiply 9 by the value obtained from step 2, which is x + 2. Therefore, the algebraic expression becomes 9(x + 2).
In summary, the phrase "The product of 9 and two more than a number" can be algebraically expressed as 9(x + 2), where x represents the number.
Learn more about algebraic expression:
https://brainly.com/question/4344214
#SPJ11
I need help i cant figure out what im doing wrong, im confused (just number 15)

Answers
the length of the sections will be 24 and 18 respectively.
What are parallel lines?Parallel lines are lines in a plane that are always the same distance apart. Parallel lines never intersect. Perpendicular lines are lines that intersect at a right (90 degrees) angle.
Given, Some pair of lines in that three lines are parallel and two of them are intersecting them.
Since, these are the the section made by two parallel lines. Thus, these given section will be Proportional to each other.
Thus,
20/15 = ( 7x - 11)/(4x - 2)
4/3 = ( 7x - 11)/(4x - 2)
16x - 8 = 21x - 33
5x = 25
x = 5
therefore, the length of the sections will be 24 and 18 respectively.
Learn more about parallel lines here:
https://brainly.com/question/28969931
#SPJ1
find the particular solution of y''' = 0 given that: y(0) = 3, y'(1) = 4, y''(2) = 6
Answers
The particular solution of y''' = 0, with initial conditions y(0) = 3, y'(1) = 4, y''(2) = 6, is y(x) = 3x² - 2x + 3.
To find the particular solution of the differential equation y''' = 0, we need to integrate the equation multiple times. Let's proceed step by step:
First, integrate the equation y''' = 0 with respect to x to obtain y''(x):
∫(y''') dx = ∫(0) dx
y''(x) = C₁
Here, C₁ is the constant of integration.
Integrate y''(x) = C₁ with respect to x to find y'(x):
∫(y'') dx = ∫(C₁) dx
y'(x) = C₁x + C₂
Here, C₂ is the constant of integration.
Integrate y'(x) = C₁x + C₂ with respect to x to determine y(x):
∫(y') dx = ∫(C₁x + C₂) dx
y(x) = (C₁/2)x² + C₂x + C₃
Here, C₃ is the constant of integration.
Now, we can apply the given initial conditions to find the particular solution:
Using y(0) = 3:
y(0) = (C₁/2)(0)² + C₂(0) + C₃ = 0 + 0 + C₃ = C₃ = 3
Using y'(1) = 4:
y'(1) = C₁(1) + C₂ = C₁ + C₂ = 4
Using y''(2) = 6:
y''(2) = C₁ = 6
From the equation C₁ + C₂ = 4, and substituting C₁ = 6, we can solve for C₂:
6 + C₂ = 4
C₂ = 4 - 6
C₂ = -2
Therefore, C₁ = 6, C₂ = -2, and C₃ = 3. Plugging these values back into the equation y(x), we obtain the particular solution:
y(x) = (6/2)x² - 2x + 3
y(x) = 3x² - 2x + 3
Hence, the particular solution of the given differential equation y''' = 0, satisfying the initial conditions y(0) = 3, y'(1) = 4, y''(2) = 6, is y(x) = 3x² - 2x + 3.
To know more about particular solution,
https://brainly.com/question/28688394
#SPJ11
1. If α and β are the zeroes of a polynomial such that α + β = -6 and αβ = 5, then find the polynomial.
Answers
Answer:
\( {x}^{2} + 6x + 5\)
Step-by-step explanation:
Required polynomial
\( {x}^{2} - ( \alpha + \beta )x + \alpha \beta \\ \\ = {x}^{2} - ( - 6)x + 5 \\ \\ = {x}^{2} + 6x + 5\)
I need help with questions in the photo this is from Khan Academy precalculus trigonometry section

Answers
Answer:
Step-by-step explanation:
okay first stop trying to make me do your test, and second get smarter its so easy.
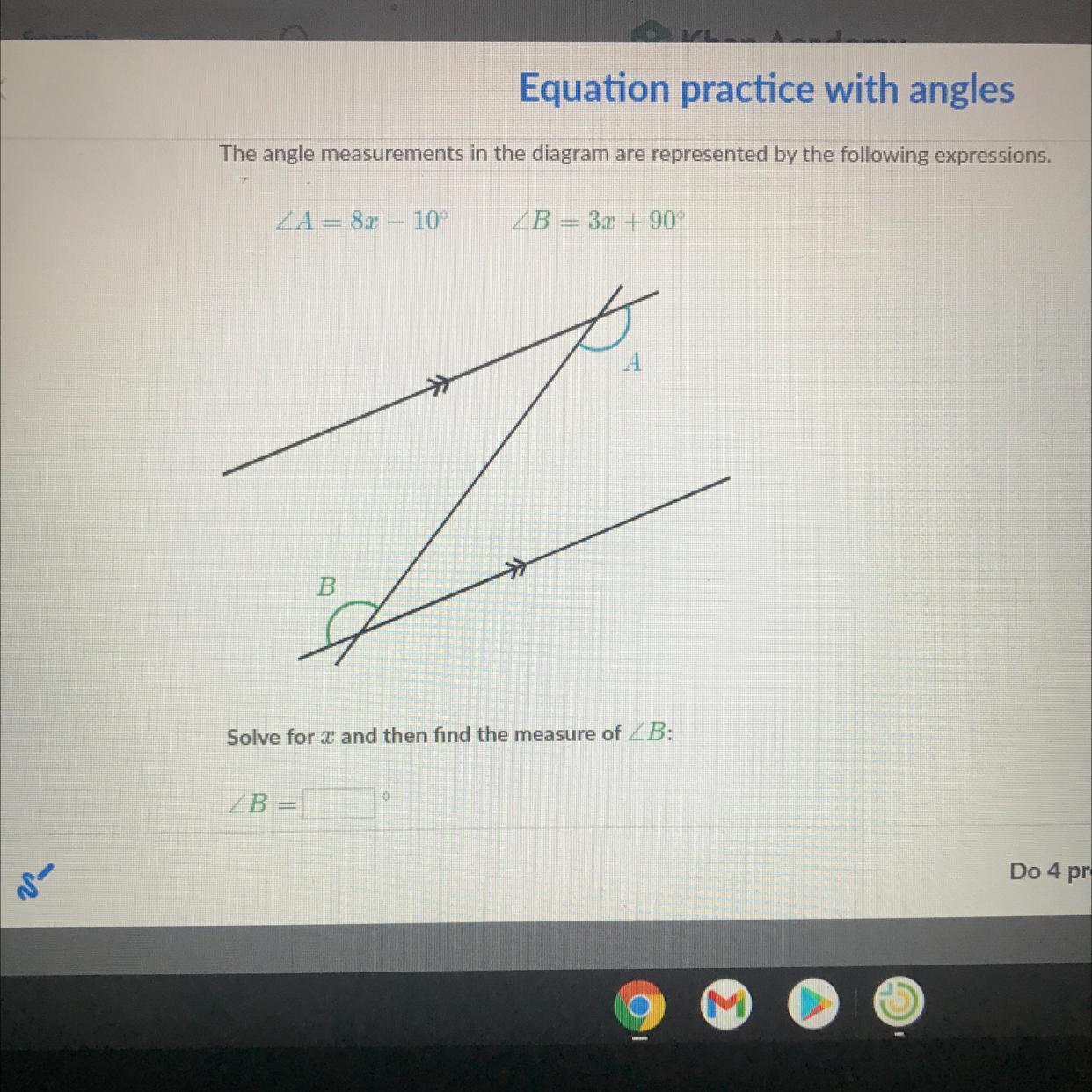
Please solve for X and Find the measure of B.
Answers
Answer:
\(\angle B=150^{\circ}\)
Step-by-step explanation:
The diagram is two parallel lines cut by a transversal therefore Angle A and Angle B are alternate interior angles, in this case meaning they are equivalent (because lines are parallel).
We can use this information to set up an equation:
\(8x-10=3x+90\)
Add 10 to both sides:
\(8x=3x+100\)
Subtract 3x from both sides
\(5x=100\)
Divide both sides by 5
\(x=20\)
Then, substitute 20 for x to solve for Angle B:
\(\angle B=3(20)+90\\\angle B=60+90\\\angle B=150\)
solving systems by substitution x+y=10
4x-3y=12
Answers
Answer:
x = 6
y = 4
Step-by-step explanation:
x+y=10
4x-3y=12
Times the first equation by three and solve
3x + 3y = 30
4x - 3y = 12
7x = 42
x = 6
Then put 6 back in to solve for y
4(6) - 3y = 12
24 - 3y = 12
-3y = -12
y = 4
Let's check
6 + 4 = 10
10 = 10
So, my answer is correct!
Stefan sells Jin a bicycle for $173 and a helmet for $19. The total cost for Jim is 160% of what Stefan spent originally to buy the bike and helmet. How much did Stephan spend originally. How much money did he make by selling the bicycle and helmet to him
Answers
Answer:
120$ 60$
Step-by-step explanation:
The total cost 161+19=180
180X150%=180×1.5
= = 120
150%=15, the rule of multiplication
" Stefan spend originally $120. 180-120=60
He make $60 by selling the bicycle and helmet to Jin.
∂²p/∂r² + 1/r ∂p/∂r = ϕμC/k ∂p/∂t
derivation of equations
1-partial derivative diffusivity equation spherical flow
2- partial derivative diffusivity equation hemi- spherical flow
Answers
The partial derivative diffusivity equation for spherical flow is ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t, and for hemispherical flow, it is the same equation.
1. The partial derivative diffusivity equation for spherical flow is derived from the spherical coordinate system and applies to radial flow in a spherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
2. The partial derivative diffusivity equation for hemispherical flow is derived from the hemispherical coordinate system and applies to radial flow in a hemispherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
1. For the derivation of the partial derivative diffusivity equation for spherical flow, we consider a spherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the polar angle (φ). By assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in spherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
2. Similarly, for the derivation of the partial derivative diffusivity equation for hemispherical flow, we consider a hemispherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the elevation angle (ε). Again, assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in hemispherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
In both cases, the term ϕμC/k ∂p/∂t represents the source or sink term, where ϕ is the porosity, μ is the fluid viscosity, C is the compressibility, k is the permeability, and ∂p/∂t is the change in pressure over time.
These equations are commonly used in fluid mechanics and petroleum engineering to describe radial flow behavior in spherical and hemispherical geometries, respectively.
To learn more about partial derivative, click here: brainly.com/question/2293382
#SPJ11
hello pls solve it...

Answers
For a sale of Rs 15,000, the commission received by the agent is Rs 150.
For a sale of Rs 25,000, the commission received by the agent is Rs 325.
For a sale of Rs 55,000, the commission received by the agent is Rs 1,225.
To calculate the commission received by the agent for different sales amounts, we'll follow the given commission rates based on the sales tiers.
For a sale of Rs 15,000:
Since the sale amount is less than Rs 20,000, the commission rate is 1%.
Commission = Sale amount * Commission rate
Commission = 15,000 * 0.01
Commission = Rs 150
For a sale of Rs 25,000:
Since the sale amount is greater than Rs 20,000 but less than Rs 50,000, we'll calculate the commission in two parts.
First, for the amount up to Rs 20,000:
Commission = 20,000 * 0.01
Commission = Rs 200
Next, for the remaining amount (Rs 25,000 - Rs 20,000 = Rs 5,000):
Commission = 5,000 * 0.025
Commission = Rs 125
Total commission = Commission for up to Rs 20,000 + Commission for the remaining amount
Total commission = Rs 200 + Rs 125
Total commission = Rs 325
For a sale of Rs 55,000:
Since the sale amount is greater than Rs 50,000, we'll calculate the commission in three parts.
First, for the amount up to Rs 20,000:
Commission = 20,000 * 0.01
Commission = Rs 200
Next, for the amount between Rs 20,000 and Rs 50,000 (Rs 55,000 - Rs 20,000 = Rs 35,000):
Commission = 35,000 * 0.025
Commission = Rs 875
Finally, for the remaining amount (Rs 55,000 - Rs 50,000 = Rs 5,000):
Commission = 5,000 * 0.03
Commission = Rs 150
Total commission = Commission for up to Rs 20,000 + Commission for the amount between Rs 20,000 and Rs 50,000 + Commission for the remaining amount
Total commission = Rs 200 + Rs 875 + Rs 150
Total commission = Rs 1,225
for such more question on commission
https://brainly.com/question/17448505
#SPJ8
\(\frac{3}{2x}\)-\(\frac{11}{5}\)=\(\frac{7}{8}\).\(\frac{64}{49}\)
Answers
Answer:
x=35/78
Step-by-step explanation:
3/2x-11/5=(7/8)*(64/49)
3/2x-11/5=8/7
3/2x=8/7+11/5
3/2x=117/35
x=(35*3)/(2*117)
x=35/78
How to Rotate (9,3) clockwise by 90*?
Answers
Answer:
Rotation of point through 90° about the origin in clockwise direction when point M (h, k) is rotated about the origin O through 90° in clockwise direction. The new position of point M (h, k) will become M’ (k, -h).
1000000000000000000000000000

Answers
Answer:
1. List (in order) the five phases a single 2 solar mass will go through in its life.
2. List (in order) the five phases a single 25 solar mass will go through in its life.
3. List (in order) the five phases a single 60 solar mass will go through in its life.
Phase options (can be used more than once, some may not be used at all):
Type II Supernova
Protostar
White Dwarf
Giant Phase
Main sequence
Neutron Star
Brown Dwarf
Black Hole
Type 1a Supernova
Planetary Nebula
Step-by-step explanation:
A phone company offers two monthly plans. Plan A costs $22 plus and
additional $0.09 for each minute of calls. Plan B costs $8 plus an
additional $0.14 for each minute of calls. For what amount of calling do
the two plans cost the same?
Answers
Answer:
Step-by-step explanation:
Plan A = 30 +0.15x
Plan B = 16 +0.20x
30+0.15x = 16+0.20x
subtract 16 from each side
14 +0.15x = 0.20x
subtract 0.15x from each side
14=0.05x
x = 14/0.05 = 280 minutes
280*0.15 = 42 +30 = $72
280 * 0.20 = 56 +16 = 72
280 minutes and cost $72 each
Given cos θ = - 5/11 and that is in quadrant II, the value of sin (θ + π/3) to the nearest hundredth, is ___
Answers
The value of sin (θ + π/3) given cos θ = - 5/11 and that is in quadrant II, to the nearest hundredth is approximately (√96 - 5√3)/22.
To find the value of sin (θ + π/3) given cos θ = -5/11 and θ is in quadrant II, we can use the trigonometric identity sin (θ + π/3) = sin θ * cos (π/3) + cos θ * sin (π/3). Here's the step-by-step process:
Step 1: Determine the value of sin θ using the Pythagorean identity sin²θ + cos²θ = 1:
sin θ = √(1 - cos²θ) = √(1 - (-5/11)²) = √(1 - 25/121) = √(96/121) = √96/11.
Step 2: Calculate the value of cos (π/3) and sin (π/3):
cos (π/3) = 1/2,
sin (π/3) = √3/2.
Step 3: Substitute the known values into the trigonometric identity:
sin (θ + π/3) = sin θ * cos (π/3) + cos θ * sin (π/3)
sin (θ + π/3) = (√96/11) * (1/2) + (-5/11) * (√3/2)
sin (θ + π/3) = √96/22 - 5√3/22
sin (θ + π/3) = (√96 - 5√3)/22.
To learn more about trigonometric identity click on,
https://brainly.com/question/29164837
#SPJ4
Write an equation that could be used to find the value of e.

Answers
Answer:
Last option is the correct answer.
Step-by-step explanation:
By sine rule..
\( \huge \frac{ \sin \: 45 \degree}{22} = \frac{ \sin \: 63 \degree}{e} \\ \)
The highest common factor (HCF) of 28, 36, and 48 is
A) 4
B) 48
C) 756
D) 1008
Answers
Answer: 4
Step-by-step explanation: 756 and 1008 are not factors of any of them, 48 isn't a factor of 28 or 36