Find a basis for the orthogonal complement of the subspace of R4 spanned by the vectors. v1 = (1, 4, -5, 3), v2 = (4, 15, 0, 5), v3 = (1, 3, 15, -4)
The basis for the row space is
W1 = ( ... , ... , 1, 0)
W2= (..., ..., 0, 1)
Answers
Answer:
W1 = ( -75, 20, 1 , 0 )
W2 = ( 25, -7 , 0, 1 )
Step-by-step explanation:
attached below is the remaining part of the solution
for a homogenous system of equation ; Ax = 0
x1 + 4x2 -5x3 + 3x4 = 0
-x2 + 20x3 -7x4 = 0 note: x3 and x4 are free variables
we can take x3 = 0 and x4 = 1 , hence ; x2 = -7
∴ x1 - 28 + 3 = 0 = x1 = 25
W2 = ( x1 ,x2, x3, x4 ) = ( 25, -7 , 0, 1 )
now lets take x3 = 1 and x4 = 0 hence x2 = 20 , x1 = -75
∴ W1 = ( x1 , x2 , x3, x4 ) = ( -75, 20, 1 , 0 )

Related Questions
Decide if the statement is true or false.
7 is a solution of - 4x = -28.
Answers
True
Divide by -4 on both sides and you're left with x=7
The figure is cut into 15 equal pieces. Shade 2/5 of the figure
Answers
Answer: Shade 6 pieces
Step-by-step explanation:
Because 2/5 of 15 is 6
You are preparing to buy a house. Your monthly gross income is $3,200. a. What is the maximum amount you can finance (mortgage)? (4 points)
Answers
The maximum amount you can finance is $896.
We are given that;
The monthly gross income = $3,200
Now,
28% of your gross monthly income on your mortgage, including taxes and insurance
The percentage = 28%
3200* 28/100
=32*28
=896
Therefore, by percentage the answer will be $896.
Learn more about percent here:
https://brainly.com/question/11549320
#SPJ1
What 2+2.... I need help lololololol.olo
Answers
Answer:
4
Step-by-step explanation:
2+2 is 4
! PLEASE HELP ! Mr. Herman had $120 and Mr. Chandra had $80. After each of them had paid for a concert ticket,
Mr. Herman had 3 times as much money as Mr. Chandra. (a) How much was the ticket? (b) How
much money did Mr. Chandra have left?
Answers
Answer:
Step-by-step explanation:
let x be the price of ticket,then
120-x=3(80-x)
120-x=240-3x
3x-x=240-120
2x=120
x=120/2=60
Price of ticket=$60
Mr.Chandra has 80-60=20 $ after buying the ticket.
solve for X in the figure

Answers
Answer:
35
Step-by-step explanation:
This shape has 6 sides.
Sum of interior angles of a 6 sided shape is 720.
117 + 4x - 5 + 4x - 3 + 118
+ 3x + 6 + 3x - 3 = 720
4x + 4x + 3x + 3x
+ 117 + 118 + 6 - 5 - 3 - 3 = 720
14x + 241 - 11 = 720
14x + 230 = 720
14x = 720 - 230
14x = 490
x = 490/14
x = 35
What is the sin B?
/21
B
5
2
sin (B) =
[?]
![What is the sin B?/21B52sin (B) =[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/bJqEBQdNtkeNzRPqszdQkxPqXUYlMPak.png)
Answers
Answer:
Step-by-step explanation:
sin (B) = \(\frac{2}{5}\)
A researcher claims that the variation in the salaries of elementary school teachers is greater than the variation in the salaries of secondary school teachers (the claim). A random sample of 30 elementary school teachers has a variance of $ 8324, and a random sample of 30 secondary school teachers has a variance of $2862. At α= 0.05, can the researcher conclude that the variation in the elementary school teachers' Salaries is greater than the variation in the secondary teachers' salaries? Use the P-value method.
Assume that all variables are normally distributed.
a. State the hypotheses and identify the claim.
b. Find the critical value.
c. Compute the test value.
d. Make the decision.
e. Summarize the results.
Answers
Answer:
a
The null hypothesis is \(H_o : \sigma^2_1 = \sigma^2 _2\)
The alternative hypothesis is \(H_a : \sigma_1 ^2 > \sigma^2_2\)
b
\(F_{critical} = 1.8608\)
c
\(F = 2.9085\)
d
The decision rule is
Reject the null hypothesis
e
There is sufficient evidence to support the researchers claim
Step-by-step explanation:
From the question we are told that
The first sample size is \(n_1 = 30\)
The sample variance for elementary school is \(s^2_1 = 8324\)
The second sample size is \(n_2 = 30\)
The sample variance for the secondary school is \(s^2_2 = 2862\)
The significance level is \(\alpha = 0.05\)
The null hypothesis is \(H_o : \sigma^2_1 = \sigma^2 _2\)
The alternative hypothesis is \(H_a : \sigma_1 ^2 > \sigma^2_2\)
Generally from the F statistics table the critical value of \(\alpha = 0.05\) at first and second degree of freedom \(df_1 = n_1 - 1 = 30 - 1 = 29\) and \(df_2 = n_2 - 1 = 30 - 1 = 29\) is
\(F_{critical} = 1.8608\)
Generally the test statistics is mathematically represented as
\(F = \frac{s_1^2 }{s_2^2}\)
=> \(F = \frac{8324 }{2862}\)
=> \(F = 2.9085\)
Generally from the value obtained we see that \(F > F_{critical }\) Hence
The decision rule is
Reject the null hypothesis
The conclusion is
There is sufficient evidence to support the researchers claim
4/5 times 40 =
1/6 times 48=
5/8 times 64=
Answers
Answer:
4/5 times 40 = 32
1/6 times 48= 8
5/8 times 64= 40
Step-by-step explanation:
Hope this helps chu! Credit to the person below as well!
Howard is organizing a 5-day cycling race. For each day of the race, he will choose one of 10 possible routes. If no route is to be repeated during the race, how many different route arrangements are possible?
Answers
According to the data, the number of different possibilities Howard has is: 3,628,000.
How to calculate how many possibilities Howard has for the routes of the stages of the race?To find the number of possibilities that Howar has for the routes of the stages of the race we must use the formula that is in the attached image. Additionally, we must take into account that the values of n and x correspond to the total of possible routes and the routes that he needs.
n = 10x = 5In this case, we only have to replace the values and obtain the result:
C = 10! / 5! (10-5)!C = 3,628,000Based on the information, it can be inferred that Howard has 3,628,000 chances to combine the routes in the 5 available stages of his career.
Learn more about combinations in: https://brainly.com/question/19692242
#SPJ1
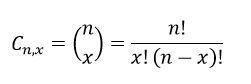
A bakery makes fruit pies and cream pies.
Twelve out of every 20 pies baked are fruit
pies. What is the ratio of cream pies to fruit
pies?
Answers
Answer:
12:20 because for ever 12 fruite pies 20 cream pies are made so it would look like the following!
12:20
Step-by-step explanation:
Hope it helps! =D
Factor the algebraic expression.
240q- 760u + 104i- 52b - 36i
Answers
f(x)=−x 2 −4x−19 find f(-9)
Answers
Answer:
64
Step-by-step explanation:
The value of the function f(x) = x² −4x−19 at the value x = -9 will be 98.
What is a function?A function in mathematics from a set X to a set Y allocates exactly one element of Y to each element of X. The sets X and Y are collectively referred to as the function's domain and codomain, respectively.
A function is defined as the expression that set up the relationship between the dependent variable and independent variable.
Given function is f(x) = x² −4x−19. The value of the function at f(-9) will be calculated as:-
f(x) = x² −4x−19
f(-9) = ( -9 )² - ( 4 x --9 ) - 19
f(-9) = 81 + 36 - 19
f(-9) = 98
Therefore, the value of the function f(x) = x² −4x−19 at the value x = -9 will be 98.
To know more about functions follow
https://brainly.com/question/17043948
#SPJ2
A 11-inch candle is lit and burns at a constant rate of 1.1 inches per hour. Let t represent the number of hours since the candle was lit, and suppose R
is a function such that R (t) represents the remaining length of the candle (in inches) t
hours after it was lit.
- What is the domain of R^−1 relative to this context? Enter your answer as an interval.
- What is the range of R^−1 relative to this context? Enter your answer as an interval.
Answers
Therefore, in response to the given query, we can state that R(-1)'s inequality possible spectrum is thus: [0, 10]
What is inequality?A connection between two expressions or numbers that is not equivalent in mathematics is referred to as an inequality. Thus, disparity results from inequity. In mathematics, an inequality establishes the connection between two non-equal numbers. Egality and disparity are not the same. Use the not equal sign most frequently when two numbers are not identical. (). Values of any size can be contrasted using a variety of disparities. By changing the two sides until only the factors are left, many straightforward inequalities can be answered. However, a number of factors support inequality: Both parts' negative numbers are divided or added. Exchange the left and the right.
The equation can be used to describe the candle's length, R(t):
R(t) = 11 - 1.1t
where t represents how long the light has been burning, in hours.
We must determine t in terms of R in order to determine the negative of R(t):
R = 11 - 1.1 t = (11 - R)/1.1 t = (11 - R)
R(t)'s inverse function is thus:
\(R^{(-1)}(R) = (11 - R)/1.1\)
0 ≤ R ≤ 11
So, R(-1)'s scope is as follows:
[0, 11]
0 ≤ R ≤ 11
Inputting these limits into the equation for R(-1) yields the following results:
\(R^{(-1)}(0) = 11/1.1 = 10\\R^{(-1)}(11) = 0/1.1 = 0\)
R(-1)'s possible spectrum is thus:
[0, 10]
To know more about inequality visit:
https://brainly.com/question/29914203
#SPJ1
Solve 2^x-2=8^4 but not solving for x
Answers
Without explicitly solving for x, we can conclude that the solution to the equation 2^x - 2 = 8^4 is x = 12.
To solve the equation 2^x - 2 = 8^4 without explicitly solving for x, we can simplify the equation using exponent rules and observe the relationship between the numbers.
First, let's simplify the equation:
2^x - 2 = 8^4
We know that 8 can be expressed as 2^3, so we can rewrite the equation as:
2^x - 2 = (2^3)^4
Applying the exponent rule (a^m)^n = a^(mn), we can simplify further:
2^x - 2 = 2^(34)
Simplifying the right side of the equation:
2^x - 2 = 2^12
Now, we can observe that both sides of the equation have the same base, which is 2. In order for the equation to hold true, the exponents must be equal:
x = 12
Therefore, we may deduce that the answer to the equation 2x - 2 = 84 is x = 12 without having to explicitly solve for x.
for such more question on equation
https://brainly.com/question/17482667
#SPJ8
NEED HELP!! I"LL GIVE YOU BRAINLIEST!! Find the value of b. a = 3 and c =12

Answers
Answer: b = 11.62
Step-by-step explanation:
We can use this formula to solve for b:
\(b^{2} =\) \(\sqrt{c^{2}-a^{2} }\)
\(b^{2} =\) \(\sqrt{12^{2}-3^2 }\)
\(b^2= \sqrt{144-9}\)
= 11.61895004
We can round that to 11.62.
Hope this helped!
The length of a rectangular backyard is represented by 4x + 10, and the width is represented by 2x + 5.
An inground swimming pool with an area of 2x² will be installed tomorrow. Write an expression to
represent the remaining area of the backyard.
(1) 8x² + 40x + 50
(3) 2x² + 6x + 15
(2) 6x² + 40x + 50
(4) 6x² + 50

Answers
Answer:
(2) 6x^2+40x +50
Step-by-step explanation:
(4x+10)*(2x+5) = 8x^2 +40+50
minus 2x^2
=6x^2 +40 +50
I need h e l p
△ABC has a right angle at C, BC=9.2 centimeters, and m∠A=63∘.
What is CA ?
Enter your answer rounded to the nearest tenth in the box.
Answers
Answer:
17.8
Step-by-step explanation:
You have to add 9.2 and 63 and the subtract from 90. Hope this helped! <3
Identify the CONCLUSION of a hypothesis test of the following claim and sample data: Claim: "The average annual household income in Warren County is $47,500." A random sample of 86 households from this county is obtained, and they have an average annual income of $48,061 with a standard deviation of $2,351. Test the claim at the 0.02 significance level.
Answers
Complete Question
The options for the above question is
a There is not sufficient evidence to warrant rejection of the claim.
b There is sufficient evidence to warrant rejection of the claim.
c There is sufficient evidence to support the claim.
d There is not sufficient evidence to support the claim.
Answer:
Option A is correct
Step-by-step explanation:
From the question we are told that
The population mean is \(\mu =\)$47,500
The sample size is \(n = 86\)
The sample mean is \(\= x =\)$48,061
The standard deviation is \(\sigma =\)$2,351
The level of significance is \(\alpha = 0.02\)
The null hypothesis is
\(H_o : \mu =\)$47,500
The alternative hypothesis is
\(H_a : \mu \ne\) $47,500
The critical value of \(\alpha\) from the t-Distribution table is \(Z_{\frac{\alpha }{2} } = 2.326\)
Now the test statistics is mathematically evaluated as
\(t = \frac{\= x - \mu }{ \frac{\sigma }{\sqrt{n} } }\)
substituting values
\(t = \frac{48061 - 47500 }{\frac{2351}{\sqrt{86} } }\)
\(t = 2.21\)
Now from the values obtained we can see that
\(Z_{\frac{\alpha }{2} } > t\)
hence we fail to reject the null hypothesis
Hence there is not sufficient evidence to warrant rejection of the claim
solve for y.
\(y + 10x = 3\)
\(y + 10x = 3\)
Answers
Y=3-10x
Hope this helped :)
Consider this expression. -3x2−24x−36 What expression is equivalent to the given expression?
Answers
The expression equivalent to the expression -3x²-24x-36 is -3(x+6)(x+2)
What is an expression?An expression in maths, a statement involving at least two different numbers (known or unknown) and at least one operation.
Given an expression, -3x²-24x-36;
Factorizing, we get,
-3x²-24x-36 = -3(x²+8x+12)
= -3(x²+6x+2x+12)
= -3[x(x+6)+2(x+6)]
= -3(x+6)(x+2)
Hence, The expression equivalent to the expression -3x²-24x-36 is -3(x+6)(x+2)
For more references on expression, click;
https://brainly.com/question/14083225
#SPJ1
I need help
1/2 + 1/3
Answers
Answer:
5/6
Step-by-step explanation:
1/2x3= 3/6
1/3x2=2/6
3/6+2/6=5/6
(a) The number of terms in an arithmetic progression is 40 and the last is -54. Given that the sum of the 15 terms added to the sum of the first 30 terms is zero. Calculate (1) The first term and common difference, (ii) the sum of the progression.
Answers
(i) The first term (a) is 24 and the common difference (d) is -2.
(ii) The sum of the progression is 2520.
i) Finding the first term and common difference:
Given that the number of terms in the arithmetic progression is 40 and the last term is -54, we can use the formula for the nth term of an arithmetic progression to find the first term (a) and the common difference (d).
The nth term formula is: An = a + (n-1)d
Using the given information, we can substitute the values:
-54 = a + (40-1)d
-54 = a + 39d
We also know that the sum of the first 15 terms added to the sum of the first 30 terms is zero:
S15 + S30 = 0
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values for S15 and S30:
[(15/2)(2a + (15-1)d)] + [(30/2)(2a + (30-1)d)] = 0
Simplifying the equation:
15(2a + 14d) + 30(2a + 29d) = 0
30a + 210d + 60a + 870d = 0
90a + 1080d = 0
a + 12d = 0
a = -12d
Substituting this value into the equation -54 = a + 39d:
-54 = -12d + 39d
-54 = 27d
d = -2
Now we can find the value of a by substituting d = -2 into the equation a = -12d:
a = -12(-2)
a = 24
Therefore, the first term (a) is 24 and the common difference (d) is -2.
ii) Finding the sum of the progression:
The sum of the first n terms of an arithmetic progression can be calculated using the formula:
Sn = (n/2)(2a + (n-1)d)
Substituting the values:
S40 = (40/2)(2(24) + (40-1)(-2))
S40 = 20(48 - 39(-2))
S40 = 20(48 + 78)
S40 = 20(126)
S40 = 2520
Therefore, the sum of the arithmetic progression is 2520.
for such more question on common difference
https://brainly.com/question/25731911
#SPJ8
can someone please answer because I need to know now !

Answers
Answer:
its option 2 because the y values don't repeat
Step-by-step explanation:
Answer:
B
Step-by-step explanation:
(someone passed this to me) 90% of people marry there 7th grade love. since u have read this, u will be told good news tonight. if u don't pass this on nine comments your worst week starts now this isn't fake. apparently if u copy and paste this on ten comments in the next ten minutes you will have the best day of your life tomorrow. you will either get kissed or asked out in the next 53 minutes someone will say i love you
Use: 0, 4, 6, 11, 9, 8, 9, 1, 5, 9, 7 to construct a box-and-whisker plot. List the maximum, minimum, and quartiles below. has to be a sentence
Answers
A box-and-whisker plot which represent the given data set is shown in the image attached below.
The five-number summary for the given data set have been listed correctly below.
What is a box-and-whisker plot?In Mathematics, a box-and-whisker plot is sometimes referred to as a box plot and it can be defined as a type of chart that is used for the graphical or visual representation of the five-number summary of a data set with respect to locality, skewness, and spread.
By using an online box-and-whisker plot calculator, the five-number summary for the given data set include the following:
Minimum = 0.First quartile = 4.Median = 7.Third quartile = 9.Maximum = 11.By critically observing the box-and-whisker plots (see attachment), we can logically deduce that all of the five-number summary for the given data set are correctly listed.
Read more on box plot here: brainly.com/question/14277132
#SPJ1

Use the Distributive Property and then Combine Like Terms (C.L.T.) to simplify: 2(3n−5)−4n+7
Answers
Answer:
Step-by-step explanation:
2(3n-5)-4n+7=
6n-10-4n+7=
-3+2n
Answer:
2n-3
Step-by-step explanation:
2(3n-5)-4n+7
6n-10-4n+7
6n-4n-10+7
2n-10+7
2n-3
Please mark me as Brainliest if you're satisfied with the answer.
Use Stirling's approximation to find an approximate formula for the multiplicity of a two-state paramagnet. Simplify this formula in the limit NN to obtain ≈ (Ne/N). This result should look very similar to your answer to Problem 2.17; explain why these two systems, in the limits considered, are essentially the same.
Answers
The simplified Stirling's approximation of the expression is Ω ≈ (Ne/N↓)^N ↓
Stirling's approximation is a method to approximate factorials of large numbers. It is given by the formula:
n! ≈ (√2πn) (n/e)ⁿ, where e is the mathematical constant approximately equal to 2.71828.
The two-state paramagnet has N spins, each of which can be either up or down. The number of possible arrangements of the N spins is 2ⁿ. However, we need to account for the fact that the energy of the system is dependent on the number of spins in the up state.
Let M be the number of spins in the up state. The energy of the system is given by E = -μBM, where μB is the Bohr magneton, and B is the magnetic field. The multiplicity of the system is given by the number of ways we can arrange the N spins such that M spins are in the up state.
Using Stirling's approximation, we can approximate the factorials involved in the multiplicity expression as follows:
Ω = (N!/(M!(N-M)!)) ≈ \(((N/e)^N / ((M/e)^M ((N-M)/e)^{N-M}))^{1/2}\)
We can simplify this expression in the limit N↓≪N, which means that the number of spins is much smaller than the total number of particles in the system. In this limit, we can make the approximation that (N-M) ≈ N.
Ω ≈ \(((N/e)^N / ((M/e)^M ((N-M)/e)^{N-M}))^{1/2}\)
Ω ≈ \(((N/e)^{N-M} / (M/e)^M)^{1/2}\)
Ω ≈ ((Ne/N↓)^ⁿ↓)
This is similar to the result obtained in Problem 2.17, which was for a system of N distinguishable particles distributed among g energy levels. In the limit where the number of particles in each energy level is much smaller than the total number of particles in the system, we obtain a similar formula for the multiplicity.
To know more about Stirling's approximation here.
https://brainly.com/question/29740229
#SPJ4
what is the Y-intercept of the graph below.

Answers
Answer:
2
Step-by-step explanation:
the line meets the y axis at (0,2)
Answer:
you need this ?
the y is
y=-x+2
Which expression is equivalent to -3(2x - 8) + 4x?
Answers
Answer:
- 2x + 24
Step-by-step explanation:
- 3(2x - 8) + 4x ← distribute parenthesis by - 3
= - 6x + 24 + 4x ← collect like terms
= - 2x + 24 or 24 - 2x
Hey there!
-3(2x - 8) + 4x
DISTRIBUTE -3 within the parentheses
= -3(2x) - 3(-8) + 4x
= -6x + 24 + 4x
COMBINE the LIKE TERMS
= (-6x + 4x) + (24)
= -6x + 4x + 24
= -2x + 24
Therefore, your answer should be:
-2x + 24
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
Malcolm has $50 gift card to a local car wash and order is the ultimate car wash each visit is $8.95
Answers
The amount cheaper is the car washes Malcolm orders than the car washes Martha's order is $13.
The correct answer choice is option B.
How much cheaper is the car washes Malcolm orders than the car washes Martha's order?Malcolm's gift card = $50.
Cost Malcolm's car wash per visit = $7
Martha's gift card = $180
Cost Martha's car wash per visit = Difference between gift card balance of first and second visit
= $180 - $160
= $20
How cheap is the car washes Malcolm orders than the car washes Martha's order = $20 - $7
= $13
Therefore, Malcolm's car wash is cheaper than Martha's car wash by $13
The complete question is attached in the diagram.
Read more on graphs:
https://brainly.com/question/19040584
#SPJ1
