Expand and simplify:
3(2p - 5) + 2(p + 3)

The probability of success, p, is the same for each trial. Each outcome is either a success (P) or a failure (Q). The correct option is A.

Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes.

You should perform x trials until you observe a success.

We have given that,

There are exactly two possible outcomes success and failure.

We have to determine the following is NOT a common characteristic of a binomial distribution.

By process of elimination:-

A binomial experiment is a statistical experiment that must meet certain requirements

All trials are independent.

There are a fixed number of n trials.

The probability of success, p, is the same for each trial.

To learn more about the probability visit:

brainly.com/question/24756209

#SPJ1

To find the magnitude (|u|) and unit vector in the direction of a vector u, you can use the following formula:

|u| = √ux2 + uy2 + uz2

Where ux, uy, and uz are the components of the vector.

Then, the unit vector in the direction of u is given by:

uhat = (ux/|u|, uy/|u|, uz/|u|).

Therefore, for exercises 7-12, find the magnitude (|u|) of the given vector, then divide each component of the vector by the magnitude to obtain the unit vector.

For example, if u = (3, 4, -5), then |u|= √32 + 42 + (-5)2 = √74 = 8.66.

The unit vector in the direction of u would then be (3/8.66, 4/8.66, -5/8.66).

To know more about  unit vector refer here:

https://brainly.com/question/30279109

#SPJ11

The rational numbers from the given numbers are -5/7, -6/7, 1/7, 2/7,3/7.

According to the statement

we have to find that the rational numbers.

So, For this purpose, we know that the

Rational number, a number that can be represented as the quotient p/q of two integers such that q ≠ 0.

From the given information:

The given numbers are between -1/2 and 4/7

Then to find the numbers then

Rational numbers = (-1/2 +4/7) /2

Rational numbers = (-1 +2/7)

Rational numbers = -5/7.

And then the number becomes -6/7, 2/7,3/7.

Now, The rational numbers from the given numbers are -5/7, -6/7, 1/7, 2/7,3/7.

So, The rational numbers from the given numbers are -5/7, -6/7, 1/7, 2/7,3/7.

Learn more about rational numbers here

https://brainly.com/question/12088221

#SPJ9

Answer:

The coordinates of B is (-5, 4).

The height of the waterfall is approximately 309 yards.

To find the height of the waterfall, we can use trigonometry. The given information states that the distance from the point to the waterfall is 1000 yards, and the angle from the ground to the top of the waterfall is 17 degrees.

We can use the tangent function, which relates the height (opposite side) to the distance (adjacent side) and the angle:

tan(angle) = height / distance

Substituting the given values:

tan(17 degrees) = height / 1000 yards

To isolate the height, we can multiply both sides of the equation by 1000:

1000 * tan(17 degrees) = height

Using a calculator, we can calculate the value of the tangent of 17 degrees:

tan(17 degrees) ≈ 0.309

Substituting this value:

1000 * 0.309 = height

Therefore, the height of the waterfall is approximately 309 yards.

To learn more about trigonometry visit:

brainly.com/question/12068045

#SPJ11

After  solving the equation 5(X - C)  = D , for the given matrices , we get , the unknown matrix X is = \(\left[\begin{array}{ccc}5&9\\10&6\\6&8\end{array}\right]\) .

In the question ,

it is given that , the matrices are

A = \(\left[\begin{array}{ccc}7&3\\4&3\end{array}\right]\)   B = \(\left[\begin{array}{ccc}7&2\\7&2\end{array}\right]\)   C = \(\left[\begin{array}{ccc}3&3\\4&0\\0&8\end{array}\right]\)   and D = \(\left[\begin{array}{ccc}10&30\\30&30\\30&0\end{array}\right]\) .

and the equation is given as 5(X - C)  = D ,

and we have to find the value of unknown matrix X .

let the matrix X be = \(\left[\begin{array}{ccc}a&b\\c&d\\e&f\end{array}\right]\)

Substituting , the given matrices A , B , C and D in the equation 5(X - C)  = D ,

we get ,

5(X - C)  = D ,

5X - 5C = D ,

5\(\left[\begin{array}{ccc}a&b\\c&d\\e&f\end{array}\right]\) - 5\(\left[\begin{array}{ccc}3&3\\4&0\\0&8\end{array}\right]\) = \(\left[\begin{array}{ccc}10&30\\30&30\\30&0\end{array}\right]\)

5\(\left[\begin{array}{ccc}a&b\\c&d\\e&f\end{array}\right]\) = \(\left[\begin{array}{ccc}10&30\\30&30\\30&0\end{array}\right]\) - \(\left[\begin{array}{ccc}15&15\\20&0\\0&40\end{array}\right]\)

Simplifying further ,

we get ,

5\(\left[\begin{array}{ccc}a&b\\c&d\\e&f\end{array}\right]\) = \(\left[\begin{array}{ccc}25&45\\50&30\\30&40\end{array}\right]\)

Dividing both sides by 5 ,

we get ,

X = \(\left[\begin{array}{ccc}a&b\\c&d\\e&f\end{array}\right]\) = \(\left[\begin{array}{ccc}5&9\\10&6\\6&8\end{array}\right]\)

Therefore , the matrix X is = \(\left[\begin{array}{ccc}5&9\\10&6\\6&8\end{array}\right]\) .

The given question is incomplete , the complete question is

Solve the matrix equation for the unknown matrix X.

A = \(\left[\begin{array}{ccc}7&3\\4&3\end{array}\right]\)   B = \(\left[\begin{array}{ccc}7&2\\7&2\end{array}\right]\)   C = \(\left[\begin{array}{ccc}3&3\\4&0\\0&8\end{array}\right]\)   and D = \(\left[\begin{array}{ccc}10&30\\30&30\\30&0\end{array}\right]\) . the equation is

5(X - C)  = D .

Learn more about Matrix here

https://brainly.com/question/7172481

#SPJ4

Answer:

After multiplying, we get two Pythagorean triples (sorry for not writing it all out, it's a really long process). With those, we can simplify down to 289/100

Answer:

12.

Step-by-step explanation:

Answer:

Table: 105 cm

Step-by-step explanation:

"m" = mouse

"c" = cat

"t" = table

equations:

t + c - m = 120

t - c + m = 90

___________

2t = 210

t = 210/2 = 105

Hope this helps

Answer:

292 m² of roof material is needed to cover the roof.

Step-by-step explanation:

In order to find how much roof material is needed to cover the roof, we must find the total amount of the area of the roof.

Because the roof is made of 4 trapezoids, we must use the formula:

Area= [(A+B)/2] × H

A and B represents the two parallel lines while H represents the height.

In order to solve the equation, you must use the Order of Operations, PEMDAS.

P= Parenthesis

E= Exponents and roots

M= Multiplication

D= Division

A= Addition

S= Subtraction

(If there is a parenthesis inside a parenthesis. Start by simplifying the parenthesis in the inside).

So:

A.The first set of two trapezoids

Area = [(14 + 6)/2] × 8

= [(20)/2] × 8

= 10 × 8

= 80 m²

One trapezoid is equal to 80 m². In order to find the total amount of both trapezoids, multiply the amount by 2.

So: 80 × 2= 160 m²

The total amount of both trapezoids is 160 m².

B.The second set of two trapezoids

Area= [(12 + 10)/2] × 6

= [(22)/2] × 6

= 11 × 6

= 66 m²

One trapezoid is equal to 66 m². In order to find the total amount of both trapezoids, multiply the amount by 2.

So: 66 × 2= 132 m²

The total amount of both trapezoids is 132 m².

Last step is to add both amounts in order to know the total amount needed of roof material that covers the roof.

So: 160 + 132= 292 m²

So the amount of roof material needed to cover the roof is 292 m².

I hope this helps! I'm sorry if its wrong or too complicated.

Answer:

-4 ≤ x ≤ 6

Step-by-step explanation:

When we talk of the domain, we are referring to the possible x-values

from the diagram, we can see that we have the x-values at -4 and 6

The dotted line means that -4 and 6 are in the domain

Thus, the two points represent the end and starting point of the domain

Writing this in interval notation, we have the representation as;

-4 ≤ x ≤ 6

Answer:

This may not be correct because it is generated by system. (High chance for it to be very accurate machine these days don't make mistake).

The one that contains horizontal line is question 2.

Please tell me if there is anything not going along.

Answer:

6x-3y+12=0

X-INTERCEPTS

Plug y=0 into the equation and solve the resulting equation 6x+12=0 for x.

The x-intercept: (−2,0)

Y-INTERCEPTS

Plug x=0 into the equation and solve the resulting equation 12−3y=0 for y.

The y-intercept: (0,4)

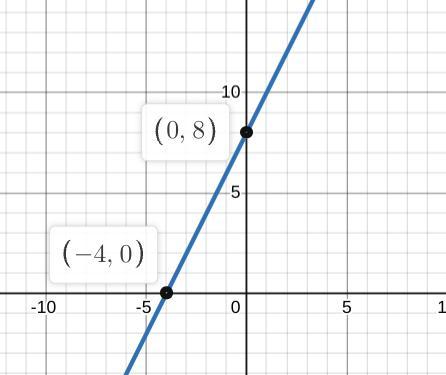
2x-y+8=0

X-INTERCEPTS

Plug y=0 into the equation and solve the resulting equation 2x+8=0 for x.

The x-intercept: (−4,0)

Y-INTERCEPTS

Plug x=0 into the equation and solve the resulting equation 8−y=0 for y.

The y-intercept: (0,8)

X+y=2

X-INTERCEPTS

Plug y=0 into the equation and solve the resulting equation x=2 for x.

The x-intercept:(2,0)

Y-INTERCEPTS

Plug x=0 into the equation and solve the resulting equation y=2 for y.

The y-intercept: (0,2)

2x-2y=4

X-INTERCEPTS

Plug y=0 into the equation and solve the resulting equation 2x=4 for x.

The x-intercept: (2,0)

Y-INTERCEPTS

Plug x=0 into the equation and solve the resulting equation −2y=4 for y.

The y-intercept: (0,−2)

We get domain from X-axis:

Answer:

5/6 divided by 1/3 = 15/6

Step-by-step explanation:

(5/6)/(1/3) = (5/6)(3/1) = 15/6

Now, (5/6)x(1/3) = 5/18

The derivative of \(r\) with respect to \(\theta\) can be found using the chain rule. Let's proceed with the differentiation:

\frac{dr}{d\theta} = \frac{d}{d\theta}\left(\cos\left(\frac{\theta}{3}\right)\right)

To differentiate \(\cos\left(\frac{\theta}{3}\right)\), we treat \(\frac{\theta}{3}\) as the inner function and differentiate it using the chain rule. The derivative of \(\cos(u)\) with respect to \(u\) is \(-\sin(u)\), and the derivative of \(\frac{\theta}{3}\) with respect to \(\theta\) is \(\frac{1}{3}\). Applying the chain rule, we have:

\frac{dr}{d\theta} = -\sin\left(\frac{\theta}{3}\right) \cdot \frac{1}{3}

Now, let's evaluate this derivative at \(\theta = \pi\):

\frac{dr}{d\theta} \bigg|_{\theta=\pi} = -\sin\left(\frac{\pi}{3}\right) \cdot \frac{1}{3}

The value of \(\sin\left(\frac{\pi}{3}\right)\) is \(\frac{\sqrt{3}}{2}\), so substituting this value, we have:

\frac{dr}{d\theta} \bigg|_{\theta=\pi} = -\frac{\sqrt{3}}{2} \cdot \frac{1}{3} = -\frac{\sqrt{3}}{6}

Therefore, the slope of the tangent line to the polar curve \(r = \cos(\theta / 3)\) at the point specified by \(\theta = \pi\) is \(-\frac{\sqrt{3}}{6}.

Learn more about Tangent Line here :

https://brainly.com/question/31179315

#SPJ11

Answer:

5 : 7

Step-by-step explanation:

groom's side: 40

bride's side: 56

ratio groom to bride = 40/56 = 20/28 = 10/14 = 5/7

Answer: 5 : 7

If events A and B are independent with P(A) = 0.68 and P(A and B) = 0.544 then the value of P(B) is 0.8

We know that if events A and B are independent, then:

P(A and B) = P(A) × P(B)

We are given P(A) = 0.68 and P(A and B) = 0.544.

Substituting these values into the equation above, we get:

0.544 = 0.68 × P(B)

Solving for P(B), we get:

P(B) = 0.544 / 0.68 = 0.8

P(B) = 0.800

Hence, if events A and B are independent with P(A) = 0.68 and

P(A and B) = 0.544 then the value of P(B) is 0.8

To learn more on probability click:

https://brainly.com/question/11234923

#SPJ1

Answer:

Days       Hours

  1              24

  2             48

  3             72

  4             96

  5            120

  6            144

Step-by-step explanation:

hope this helped:) just add lines and it will be a table

Answer:

x-intercept is 8, meaning if you get 8 candy bars, you can get 0 popcorn bags.

y-intercept is 6, meaning if you get 6 popcorn bags, you can get 0 candy bars. When Jackie had 0 candy bars, she had 6 (y-intercept) bags of popcorn and when Jackie had 0 bags of popcorn, she had 8 (x-intercept) bars of candy.

Step-by-step explanation:

The y-axis represents the amount of popcorn bags she has and the x-axis has the amount of candy bars. When the linear line intercepts with either axis, at least one axis is always at zero.

Answer:

268 hope i helped

Step-by-step explanation:

Answer:

268!

Step-by-step explanation:

You can easily g0ogle this so you don't need to waste points!  

Answer: 120m2

Step-by-step explanation:8x11=88

19-11=8- length of triangle base. 1/2 base x height= 4x8=32

32+88=120m2

If two polygons are similar the corresponding angles between the two polygons must be congruent (have equal measures).

If two polygons are similar, it means that they have the same shape but possibly different sizes. In this case, the corresponding angles between the two polygons must be congruent (have equal measures).

More formally, if two polygons are similar, then their corresponding angles are equal. This property holds true for all corresponding angles of similar polygons, regardless of the number of sides or the size of the polygons.

It is a fundamental property of similarity in geometry.

Therefore, if you have two similar polygons, you can conclude that the corresponding angles of those polygons will be congruent.

To know more about polygons

https://brainly.com/question/12622435

#SPJ11

Answer:

O rotated

Step-by-step explanation:

Answer:

V = π(8^2)(31) = 6,232.9 m^3

15th row of the Pascal's Triangle is used to expand \((2x+10y)^{15}\). There will be 16 terms in the expansion.

Pascal's Triangle is used to find the co-efficient for binomial expansions.

The nth row of the Pascal's Triangle gives the coefficients in the expansion of binomial expressions of degree n. For example, in the expansion of \((x+y)^2\) , the binomial coefficients are 1,2,1 which is given in the 2nd row of Pascal's Triangle. Also the expansion has three terms, therefore. The Pascal triangle starts with 0th row consisting of only 1.

Here the given expression is \((2x+10y)^{15}\) of degree 15. So its binomial coefficient is given in the 15th row of Pascal's triangle.

The number of terms in the binomial expansion of degree n will be n+1 because the coefficients in nth row will n+1 in number.

Hence there will be 16 terms in the expansion of \((2x+10y)^{15}\).

Learn more about Pascal's Triangle at https://brainly.com/question/11995132

#SPJ4

Answer:

The person above helped, and below I've attached a ss with all of the parts of this question answered - Hope it helps!

Step-by-step explanation:

Brainliest would be very much appreciated :) - hope you have a good day!

Answer:

342.938 cm²

Step-by-step explanation:

Area of shaded region = area of rectangle - area of circle

= (length*width) - (π*radius²)

= (32*17) - (π8²)

= 544 - 201.06192983

= 342.93807017 ≈ 342.938 cm²

Answer:

x ≥ - 7

Step-by-step explanation:

3(x - 4) ≥ 5x + 2

3x - 12 ≥ 5x + 2

3x - 12 + 12 ≥ 5x + 2 + 12

3x - 5x ≥ 5x - 5x + 14

- 2x ≥ 14

- 2x ÷ - 2 ≥ 14 ÷ - 2

x ≥ - 7

Answer:

the x equals 14

Step-by-step explanation:

hope it helps

Answer:

x = - \(\frac{4}{3}\), x = - 1

Step-by-step explanation:

Given

(x + 1)(3x + 4) = 0

Equate each factor to zero and solve for x

x + 1 = 0 ⇒ x = - 1

3x + 4 = 0 ⇒ 3x = - 4 ⇒ x = - \(\frac{4}{3}\)

Solutions from least to greatest are

x = - \(\frac{4}{3}\) , x = - 1