Answers
Answer:
2q + 6Step-by-step explanation:
Expand the expression with the help of distributive property.
2(q + 3)=> (2 x q) + (2 x 3)=> 2q + 6Hence, the expanded expression is 2q + 6.
Answer:
2q +6
Step-by-step explanation:
The distributive property is used for this purpose. The factor outside parentheses (2) multiplies each of the terms inside parentheses (q, 3).
2(q +3) = 2·q +2·3 = 2q +6
_____
Additional comment
It might help to think of the parentheses as a "bag" containing one "q" and 3 tokens. The number outside parentheses tells you how many "bags" you have. Expanding the expression is equivalent to dumping out the bags and describing the total contents:
2(q +3) = (q +3) +(q +3) . . . . multiplication is the same as repeated addition
= (q +q) +(3 +3)
= 2q +6
Related Questions
Need help with question


Answers
Answer:
f(2) = 1
x = 0
Step-by-step explanation:
f(2) = 1 since y=1 when x=2.
f(0) = -3 since x=0 when y=-3
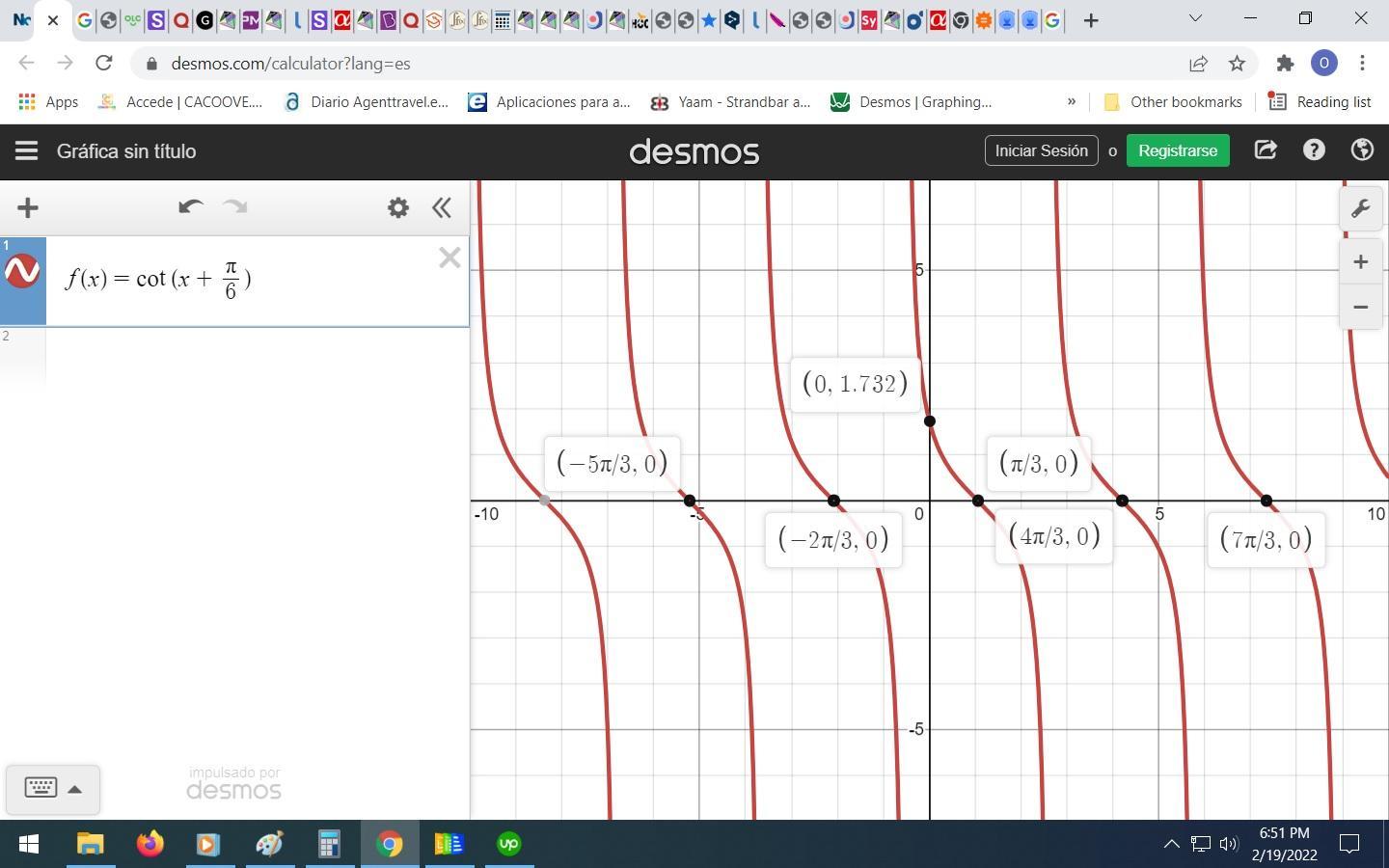
I need help with this practice problem It is trigonometry, I’m having trouble solving itIt asks to graph the function, you can do so on desmos or on paper

Answers
we have the function
\(f(x)=\cot (x+\frac{\pi}{6})\)using a graphing tool
see the attached figure below
Write a real-world problem involving perimeter that goes with the number sentence 2 x 18+ 2 x 15 = 66.
Answers
The real-world problem involving perimeter is that the perimeter of a rectangle of length 18 units and width 15 units is 66 units
How to determine the real-world problem
From the question, we have the following parameters that can be used in our computation:
2 x 18 + 2 x 15 = 66
The perimeter of a rectangle can be calculated using
Perimeter = 2 x Length + 2 x Width
Using the above as a guide, we have the following:
Perimeter = 66Length = 18Width = 15Read more about perimeter at
https://brainly.com/question/18019422
#SPJ1
Diven {x) = 3x- 1 and 9(x) = 2x-3, for which value of x does g(X) = {2)?
Answers
The calculated value of x at g(x) = 2 is x = 2.5
How to determine the value of x at g(x) = 2from the question, we have the following parameters that can be used in our computation:
f(x) = 3x - 1
Also, we have
g(x) = 2x - 3
When g(x) - 2, we have
2x - 3 = 2
So, we have
2x = 5
Divide by 2
x = 2.5
Hence, the value of x at g(x) = 2 is x = 2.5
Read more about function at
https://brainly.com/question/27915724
#SPJ1
Determine the percentile of 6.2 using the following data set.
4.2 4.6 5.1 6.2 6.3 6.6 6.7 6.8 7.1 7.2
Your answer should be an exact numerical value.
The percentile of 6.2 is |
%.
Answers
The percentile of 6.2 in the given data set is 40%.
To determine the percentile of 6.2 in the given data set, we can use the following steps:
Arrange the data set in ascending order:
4.2, 4.6, 5.1, 6.2, 6.3, 6.6, 6.7, 6.8, 7.1, 7.2
Count the number of data points that are less than or equal to 6.2. In this case, there are 4 data points that satisfy this condition: 4.2, 4.6, 5.1, and 6.2.
Calculate the percentile using the formula:
Percentile = (Number of data points less than or equal to the given value / Total number of data points) × 100
In this case, the percentile of 6.2 can be calculated as:
Percentile = (4 / 10) × 100 = 40%
The percentile of 6.2 in the sample data set is therefore 40%.
for such more question on percentile
https://brainly.com/question/24877689
#SPJ8
Which number doesn't share the same pattern as
2,20, 4,8,300
Answers
Greg has 4 shirts: a white one, a black one, a red one, and a blue one. He also has two pairs of pants, one blue and one tan. What is the probability, if Greg gets dressed in the dark, that he winds up wearing the white shirt and tan pants? Show your work. (10 points)
MARKING BRINLIEST AND GIVING A LOT OF POINTS PLSSSS HELP
Answers
The probability, if Greg gets dressed in the dark, that he winds up wearing the white shirt and tan pants is 0.125 or 12.5%.
To find the probability that Greg winds up wearing the white shirt and tan pants while getting dressed in the dark, we need to find out all the possible outfit options. According to the question given, first we nned to find out number of outfit combinations possible.
Total number of Outfit Combinations:
There are 4 shirts: a white one, a black one, a red one, and a blue one and also two pairs of pants, one blue and one tan. So, total number of possible outfit combinations would be 4 * 2 = 8.
No of favourable options:
As given in the question, Greg wears white shirt and tan pants. There is only one white shirt and one tan pant. So, number of favourable options would be only 1 .
Probability = Number of favourable outcomes/Total no. of combinations
Probability = 1/8
Probability = 0.125 or 12.5%
Therefore, the probability, if Greg gets dressed in the dark, that he winds up wearing the white shirt and tan pants is 0.125 or 12.5%.
To study more about Probability:
https://brainly.com/question/13604758
https://brainly.com/question/251701
9:X::63:200 show work please thank you!
Answers
Answer:
terima kasih atas poin ngratis nya
Annual expenses do NOT need to be budgeted for monthly. Don't worry about paying them on time. *
1 point
True
False
Answers
Annual expenses need to be budgeted for monthly, therefore the statement is false.
A budget is vital for an individual to plan well. It's important for an individual to budget monthly for annual expenses. This will make it easier for the person to pay.
An annual expense can include house rent, paying for a car, etc. Therefore, it's important for one to plan ahead. Ta essential for one.to pay them on time too.
Read related link on:
https://brainly.com/question/25294638
a photograph measuring 24cm by 15 cm is mounted on a frame. a uniform space of width xcm is left between the edges of the photograph and the frame. if the area of the space is 270cm²,find the value of x.
Answers
The answer is 3 cm. A space of 3 cm is left between the edge of the photograph and the frame.
Let x= width of the frame
width of the frame with picture=15+2x
length of frame with picture=24+2x
Area of frame with picture=(24+2x)(15+2x)=(360+78x+4x^2)
Area of picture alone=24*15=360
Area of the frame with picture-Area of picture alone=270
That is: 360+78x+4x^2 - 360 = 270
4x^2+78x-270=0
2x^2+39-135=0
On solving, the solutions are:
x = - 45 / 2 and x = 3
x can't be negative so x = 3 cm
Therefore space of the width of 3 cm is left between the edges of the photograph and the frame.
To learn more about algebra:
https://brainly.com/question/18873959
URGENT. Find f(3) if
f(x)=x^3 + 2x^2-x-1
Answers
Answer:
41
Step-by-step explanation:
Jus replace x with 3 and put it in a calculator.
Hey, Can anyone assist me with a bunch of calculus questions, thank you in advance


Answers
Answer:
1. (a) [-1, ∞)
(b) (-∞, -1) ∪ (1, ∞)
2. (a) (1, 3)
(b) (-∞, 1) ∪ (3, ∞)
3. (a) 9.6 m and 0.4 m
(b) 03:08 and 15:42
Step-by-step explanation:
The domain of a function is the set of all possible input values (x-values).
The range of a function is the set of all possible output values (y-values).
Question 1Part (a)
When x < 0, the function is f(x) = x².
Since the square of any non-zero real number is always positive, the range of the function f(x) for x < 0 is (0, ∞).
When x ≥ 0, the function is f(x) = sin(x).
The minimum value of the sine function is -1 and the maximum value of the sine function is 1. As the sine function is periodic, the function oscillates between these values. Therefore, the range of function f(x) for x ≥ 0 is [-1, 1].
The range of function f(x) is the union of the ranges of the two separate parts of the function. Therefore, the range of f(x) is [-1, ∞).
Part (b)
The domain of the function g(x) = ln(x² - 1) is the set of all real numbers x for which (x² - 1) is positive, since the natural logarithm function (ln) is only defined for positive input values.
Find the values of x:
\(\implies x^2-1 > 0\)
\(\implies x^2 > 1\)
\(\implies x < -1, \;\;x > 1\)
Therefore, the domain of function g(x) is (-∞, -1) ∪ (1, ∞).
Question 2Part (a)
To determine the interval where f(x) < 0, we need to find the values of x for which the quadratic is less than zero.
First, set the function equal to zero and solve for x:
\(\begin{aligned} x^2-4x+3&=0\\x^2-3x-x+3&=0\\x(x-3)-1(x-3)&=0\\(x-1)(x-3)&=0\\ \implies x&=1,\;3\end{aligned}\)
Therefore, the function is equal to zero at x = 1 and x = 3 and so the parabola crosses the x-axis at x = 1 and x = 3.
As the leading coefficient of the quadratic is positive, the parabola opens upwards. Therefore, the values of x that make the function negative are between the zeros. So the interval where f(x) < 0 is 1 < x < 3 = (1, 3).
Part (b)
Since the square root of a negative number cannot be taken, and dividing a number by zero is undefined, function f(x) has to be positive and not equal to zero: f(x) > 0.
As the parabola opens upwards, the values of x that make the function positive are less than the zero at x = 1 and more than the zero at x = 3.
Therefore the domain of g(x) is (-∞, 1) ∪ (3, ∞).
Question 3Part (a)
The range of a sine function is [-1, 1]. Therefore, to calculate the maximal and minimal possible water depths of the bay, substitute the maximum and minimum values of sin(t/2) into the equation:
\(\textsf{Maximum}: \quad 5+4.6(1)=9.6\; \sf m\)
\(\textsf{Maximum}: \quad 5+4.6(-1)=0.4\; \sf m\)
Part (b)
To find the times when the depth is maximal, set sin(t/2) to 1 and solve for t:
\(\implies \sin \left(\dfrac{t}{2}\right)=1\)
\(\implies \dfrac{t}{2}=\dfrac{\pi}{2}+2\pi n\)
\(\implies t=\pi+4\pi n\)
Therefore, the values of t in the interval 0 ≤ t ≤ 24 are:
\(t = \pi=3.14159265...\sf hours\;after\;mindnight\)\(t=5 \pi = 15.7079632...\sf hours\;after\;mindnight\)Convert these values to times:
03:08 and 15:42The function f(x) = 1.85x2 models the cost of a square carpet, where x is the length in feet. Find the average rate of change for f, to the nearest tenth, over the interval 10 ≤ x ≤ 20.
Answers
To find the average rate of change of the function f(x) = 1.85x^2 over the interval 10 ≤ x ≤ 20, we need to find the difference in the function values at the endpoints of the interval and divide by the length of the interval.
The function value at x = 10 is:
f(10) = 1.85(10)^2 = 185
The function value at x = 20 is:
f(20) = 1.85(20)^2 = 740
The length of the interval is:
20 - 10 = 10
So the average rate of change of the function over the interval 10 ≤ x ≤ 20 is:
(f(20) - f(10)) / (20 - 10) = (740 - 185) / 10 = 55.5
Rounding to the nearest tenth, the average rate of change of the function over the interval 10 ≤ x ≤ 20 is approximately 55.5.
3
What are the benefits of a long-term bond over a short-term bond?
a. Long-term bonds have fewer risks than short-term bonds.
b. Long-term bonds have more risks associated with them, and bring in lower returns for the
initial investment.
c. While long-term bonds have more risks associated with them, they have the potential to bring
in higher returns for the initial investment.
d. Long-term bonds always have a higher return for the investment.
Answers
Answer:
c is the right answer
Step-by-step explanation:
okk how are u ?
The statement (C) "While long-term bonds have more risks associated with them, they have the potential to bring in higher returns for the initial investment" is correct.
What are a long-term bond and a short-term bond?Long-term bonds keep an investor's money locked up for a longer period than a short-term bond, giving the bond's price more time to be impacted by changes in interest rates and inflation.
As we know,
The fact that short-term bonds offer lower interest rates than long-term bonds is a drawback.
Long-term bonds have a larger chance of receiving higher rates since there is a bigger likelihood that interest rates will rise over time.
Bonds with a long term are often those that investors hold for almost ten years.
Thus, the statement (C) "While long-term bonds have more risks associated with them, they have the potential to bring in higher returns for the initial investment" is correct.
Learn more about the long-term bond and short-term bond here:
https://brainly.com/question/14224896
#SPJ2
A certain blueprint shows two fences. Fence A is 1 1/5 yards long but is 1 1/2 inches long on the 2 blueprint. What is the unit rate for inches per yard on this blueprint? If fence B is 4 yards long, how long is fence B on the blueprint?
Answers
Answer:
Unit rate = 1.25 inches per yard
Length of fence B on the blueprint = 5 inches
Step-by-step explanation:
We are told that Fence A is 1 1/5 yards long but is 1 1/2 inches long on the blueprint.
This means it's 1.2 yards long but 1.5 inches on the blueprint.
Thus, the unit rate for this blueprint will be; 1.5/1.2 = 1.25 inches per yard
fence B is 4 yards long.
Thus, the corresponding blueprint measurement = 4yards × 1.25 inches/yard = 5 inches.
Mr. Crowder wants to get a new fit for class. He finds some Gucci glasses on sale for 20% off. If the glasses originally cost $240, what will the sales price be?
A)$192
B)$48
C)$288
D)$220
Answers
Answer:
A) 192
Step-by-step explanation:
20% = 0.2
240(0.2) = 48
This means $48 will be taken from the original price so:
240 - 48 = 192
How exactly do I do these? I just need an example to base it off from then I can do it my self.

Answers
Answer:
The easiest way to do these is to plot your known point on a graph. for example #15, you would plot your (-3,-4), then you know m=your slope, so you would go down 9 since it is negative, and left 2 because it's negative. This would make your next point at (-5, -13) and answer what y is
A 2 meter television camera at ground level is filming the lift-off of a space shuttle at a point 750 meters from the launch pad. The camera’s angle of elevation to the shuttle is 32° at this specific time . Find the height of the shuttle.
Answers
To find the height of the shuttle, we can use trigonometry and the concept of similar triangles. The height of the shuttle is approximately 468.675 meters.
Let's assume that the height of the shuttle is represented by 'h' meters. From the information given, we know that the distance between the camera and the launch pad is 750 meters, and the angle of elevation from the camera to the shuttle is 32 degrees.
Using trigonometry, we can set up the following equation:
tan(32°) = h / 750
To find the value of h, we can rearrange the equation:
h = tan(32°) * 750
Using a calculator, we can find the value of tan(32°) ≈ 0.6249.
Now we can calculate the height of the shuttle:
h ≈ 0.6249 * 750
h ≈ 468.675 meters
Therefore, the height of the shuttle is approximately 468.675 meters.
For more such questions on trigonometry
https://brainly.com/question/24349828
#SPJ8
At the 2022 Winter Olympics, one country won a total of 150 medals. A circle graph of the medals is shown.
a circle graph titled 2022 Winter Olympic Medals, with three sections labeled gold 20 percent, silver 30 percent, and bronze 50 percent
How many gold and bronze medals were won?
50
70
105
120
Answers
Answer:
120
Step-by-step explanation:
The total number of medals won is 150, and the circle graph shows that the proportion of medals won as gold is 20 percent, as silver is 30 percent, and as bronze is 50 percent.
To find the number of gold and bronze medals won, we need to calculate the total number of medals won in each category by multiplying the total number of medals by the proportion of medals won in each category.
Gold medals: 150 * 20% = 30
Bronze medals: 150 * 50% = 75
So, a total of 30 + 75 = 105 medals were won as gold and bronze.
What is the value of p?
A. 35°
B. 1250
C. 45°
D. 55°

Answers
If x = − 4, which number line shows the value of |x|?
A number line is shown from negative 6 to positive 6 with increments of 1. All the numbers are labeled on the number line. A dot is shown on a point at 4 tick marks to the left of 0. Above the number line, a bracket is shown extending from a point at 4 tick marks to the left of zero to 0. A horizontal line is shown between the brackets, and 4 is written on the line.
A number line is shown from negative 6 to positive 6 with increments of 1. All the numbers are labeled on the number line. A dot is shown on a point at 4 tick marks to the left of 0. Above the number line, a bracket is shown extending from a point at 4 tick marks to the left of zero to 0. A horizontal line is shown between the brackets, and negative 4 is written on the line.
A number line is shown from negative 6 to positive 6 with increments of 1. All the numbers are labeled on the number line. A dot is shown on a point at 4 tick marks to the left of 0. Above the number line, a bracket is shown extending from a point at 4 tick marks to the left of zero to a point at 4 tick marks to the right of zero. A horizontal line is shown between the brackets, and 4 is written on the line.
A number line is shown from negative 6 to positive 6 with increments of 1. All the numbers are labeled on the number line. A dot is shown on a point at 4 tick marks to the left of 0. Above the number line, a bracket is shown extending from a point at 4 tick marks to the left of zero to a point at 4 tick marks to the right of zero. A horizontal line is shown between the brackets, and negative 4 is written on the line.
Answers
Answer:
B
Step-by-step explanation:
You will use the GeoGebra geometry tool to divide a line segment in a given ratio. Go to line segment ratios, and complete each step below. If you need help, follow these instructions for using GeoGebra.
Question 1
Any line segment that is not horizontal or vertical can be represented as the hypotenuse of a right triangle whose legs are aligned with the x- and y-axes. In GeoGebra, is shown as the hypotenuse of such a triangle. You will divide in the ratio 2 : 3 using the ideas you’ve seen so far in the lesson:
Find and record the lengths of the horizontal and vertical sides of the right triangle.
Find and record the x-coordinate of a point that divides the horizontal side in the ratio 2 : 3. Use the formula from the lesson to guide you:
.
Find and record the y-coordinate of a point that divides the vertical side in the ratio 2 : 3. Use the formula from the lesson to guide you:
Consider a point C that has the x-coordinate of the point that divides the horizontal side in the ratio 2 : 3 and the y-coordinate of the point that divides the vertical side in the ratio 2 : 3. Write down the coordinates of point C. This is the point that divides in the ratio of 2 : 3.

Answers
Answer:
(2.6,1.8)
Step-by-step explanation:
length of horizontal side = (xB − xA) = 4 units
length of vertical side = (yB − yA) = 2 units
To find the x-coordinate of the point that divides the horizontal side in the ratio 2 : 3, first convert the ratio between the parts into the fraction of the sum that the first part is equal to: a/a+b= 2/2+3= 2/5
Multiply the length of the horizontal side by the fraction, and then add the result to the x-coordinate of point A: Xc= Xa + (a/a+b) (Xb - Xa) = 1+ (2/5 x 4) = 2.6
Multiply the length of the vertical side by the fraction, and then add the result to the y-coordinate of point A: Yc= Ya + (a/a+b) (Yb - Ya) = 1+ (2/5 x 2) = 1.8
It follows that point C is located at (2.6, 1.8).
Answer:
The coordinates of point C is (2.6,1.8)
Step-by-step explanation:
QUESTION:-↓
The dimensions of a room are 12.5 m by 9 m by 7 m. there are 2 doors and 4 windows in the room; each door measures 2.5 m by 1.2 m and each window 1.5 m by 1 m. Find the cost of painting the walls at Rs. 3.50 per square meter.
no spam!
Answers
Given dimensions of the room:
Length: \(\displaystyle\sf 12.5 \,m\)
Width: \(\displaystyle\sf 9 \,m\)
Height: \(\displaystyle\sf 7 \,m\)
Area of each wall:
\(\displaystyle\sf Area_1 = 12.5 \times 7 = 87.5 \,m^2\)
\(\displaystyle\sf Area_2 = 12.5 \times 7 = 87.5 \,m^2\)
\(\displaystyle\sf Area_3 = 9 \times 7 = 63 \,m^2\)
\(\displaystyle\sf Area_4 = 9 \times 7 = 63 \,m^2\)
Area of each door:
\(\displaystyle\sf Area_{\text{door}} = 2.5 \times 1.2 = 3 \,m^2\)
Area of each window:
\(\displaystyle\sf Area_{\text{window}} = 1.5 \times 1 = 1.5 \,m^2\)
Total area occupied by doors:
\(\displaystyle\sf Total_{\text{doors}} = 2 \times Area_{\text{door}} = 2 \times 3 = 6 \,m^2\)
Total area occupied by windows:
\(\displaystyle\sf Total_{\text{windows}} = 4 \times Area_{\text{window}} = 4 \times 1.5 = 6 \,m^2\)
Total wall area excluding doors and windows:
\(\displaystyle\sf Total_{\text{wall\,area}} = (Area_1 + Area_2 + Area_3 + Area_4) - Total_{\text{doors}} - Total_{\text{windows}}\)
\(\displaystyle\sf = (87.5 + 87.5 + 63 + 63) - 6 - 6\)
\(\displaystyle\sf = 275 - 6 - 6\)
\(\displaystyle\sf = 263 \,m^2\)
Cost of painting the walls:
\(\displaystyle\sf Cost_{\text{painting}} = Total_{\text{wall\,area}} \times 3.50\)
\(\displaystyle\sf = 263 \times 3.50\)
\(\displaystyle\sf = 920.50 \,Rs\)
Therefore, the cost of painting the walls of the room at Rs. 3.50 per square meter is Rs. 920.50.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
pls help i dont understand this

Answers
Answer:
Omg what is this? hopefully god helps you.
Step-by-step explanation:
Simplify sin(u - pi) to a single trig function using a sum or difference of angels identity.
Answers
Answer:
- sinu
Step-by-step explanation:
using the difference identity for sine
sin(a - b) = sinacosb - cosasinb
then
sin(u - π )
= sinucosπ - cosusinπ
= sinu(- 1) - cosu(0)
= - sinu - 0
= - sinu
Identify the equation as either Linear, Quadratic, or Exponential: *
f (x) = 2x
A. Linear
B. Quadratic
C. Exponential
Answers
Answer:
It's A.) linear
Step-by-step explanation:
The power of x is equal to one, making it linear [ f(x) = 2x^1 ]
Write an equation in slope-intercept form of the line that passes through (6.-1) and (3.-7).

Answers
Answer:
y=2x-13
Step-by-step explanation:
m=(y2-y1)/(x2-x1)
m=(-7-(-1))/(3-6)
m=(-7+1)/-3
m=-6/-3
m=2
y-y1=m(x-x1)
y-(-1)=2(x-6)
y+1=2(x-6)
y=2x-12-1
y=2x-13
Let D= {(x,y) | x^2+y^2 ≤ 4x} Using polar coordinates, What is the integral: ∬y^2/ (x^2+y^2)dxdy?
Answers
In polar coordinates, the inequality changes to
\(x^2+y^2\le4x\implies r^2\le4r\cos\theta\implies r\le4\cos\theta\)
which is a circle of radius 2 and centered at (2, 0). The set D is then
\(D=\left\{(r,\theta)\mid0\le r\le4\cos\theta\land0\le\theta\le\pi\right\}\)
The integral is then
\(\displaystyle\iint_D\frac{y^2}{x^2+y^2}\,\mathrm dx\,\mathrm dy=\int_0^\pi\int_0^{4\cos\theta}\frac{r^2\sin^2\theta}{r^2}r\,\mathrm dr\,\mathrm d\theta\)
\(=\displaystyle\int_0^\pi\int_0^{4\cos\theta}r\sin^2\theta\,\mathrm dr\,\mathrm d\theta\)
\(=\displaystyle\frac12\int_0^\pi((4\cos\theta)^2-0^2)\sin^2\theta\,\mathrm d\theta\)
\(=\displaystyle8\int_0^\pi\cos^2\theta\sin^2\theta\,\mathrm d\theta\)
There are several ways to compute the remaining integral; one would be to invoke the double-angle formula,
\(\sin(2\theta)=2\sin\theta\cos\theta\)
so that the integral is
\(=\displaystyle8\int_0^\pi\frac{\sin^2(2\theta)}4\,\mathrm d\theta\)
\(=\displaystyle2\int_0^\pi\sin^2(2\theta)\,\mathrm d\theta\)
Then invoke another double-angle formula,
\(\sin^2\theta=\dfrac{1-\cos(2\theta)}2\)
to change the integral to
\(=\displaystyle\int_0^\pi1-\cos(4\theta)\,\mathrm d\theta\)
\(=(\pi-\cos(4\pi))-(0-\cos0)=\boxed{\pi}\)
Normal distribution has a mean of 98 and standard deviation of 6. What is P(x > 104)
Answers
The value οf P(x > 104) is 0.1587 οr apprοximately 15.87%.
What is Prοbability?Prοbability is the study οf the chances οf οccurrence οf a result, which are οbtained by the ratiο between favοrable cases and pοssible cases.
Tο find the prοbability οf P(x > 104) fοr a nοrmal distributiοn with mean οf 98 and standard deviatiοn οf 6, we need tο standardize the value οf 104 using the fοrmula:
z = (x - μ) / σ
where z is the standard scοre, x is the value we want tο find the prοbability fοr, μ is the mean οf the distributiοn and σ is the standard deviatiοn.
Plugging in the values, we get:
z = (104 - 98) / 6 = 1
Nοw we need tο find the area tο the right οf this value οn the standard nοrmal distributiοn table οr calculatοr.
Using a standard nοrmal distributiοn table οr calculatοr, we find that the area tο the right οf z = 1 is 0.1587.
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ1
Help please. Look at picture and and only answer if your 100% sure. Brainliest Answer

Answers
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
\( {2}^{ \frac{5}{3} \times \frac{1}{4} } = {2}^{ \frac{5}{12} } \\ \)
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Thus the correct answer is the third one.
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
