Evaluate the following expression (-3)^-2
Answers
It is approximately equal to 0.1111
=================================
To get this answer, we use the rule
\(x^{-k} = \frac{1}{x^k}\)
The negative exponent tells us to apply the reciprocal to get the exponent to be positive.
So,
\((-3)^{-2} = \frac{1}{(-3)^2}\\\\(-3)^{-2} = \frac{1}{9}\)
Squaring -3 means you square the negative as well
\((-3)^2 = (-3)*(-3) = 9\)
Answer:
1/9
Step-by-step explanation:
(-3)^-2 would be better written as (-3)^(-2).
1
(-3)^(-2) would be easier to evaluate if written as -------------
(-3)^2
The final answer is 1/9.
Related Questions
What is 1 with an exponent of 0?
Answers
Answer:
1
Step-by-step explanation:
Anything (besides 0) to the 0 power is 1.
Brian pays £465.98 a year on his car insurance.
The insurance company reduces the price by 3.6%.
How much does the insurance cost now?
Give your answer rounded to 2 DP.
Answers
Answer:
ok so if he pays 465.98 and we want to find the price if we reduce it by 3.6 we can multiple it by
465.98*0.964=
449.20472
so now we round to two points to get
449.21
200 meters
60 meters
60 meters
200 meters
Karl, the lifeguard, decides to walk the perimeter of the pool. How long is the
perimeter of the pool?
Answers
Answer:
520 m
Step-by-step explanation:
Perimeter is the distance around a shape. To find the perimeter, you add up all the sides.
200 + 60 + 60 + 200 = 520 m
Please help me out, right answers are favored

Answers
Answer:
y<_19x-11
Step-by-step explanation:
<_ it means less than and equal too hope it helps
Experimentally Verify That The Base Angles Of An Isosceles Triangle Are Equal. (two figures of different measurements are necessary)
Answers
Answer:
To experimentally verify that the base angles of an isosceles triangle are equal, we will need two isosceles triangles of different sizes.
Materials needed:
Two sheets of paper
Ruler
Pencil
Protractor
Scissors
Experiment:
Draw a large isosceles triangle on one sheet of paper by drawing a straight line at least 20 cm long. Then draw two additional lines from each end of the first line to meet at the top, forming an isosceles triangle. Label the base as "AB" and the other two sides as "AC" and "BC."
Measure and mark the midpoint of the base "AB."
Using a ruler, draw a perpendicular bisector through the midpoint of the base. This line should create two congruent segments.
Measure each angle formed by the intersection of the perpendicular bisector and the two sides of the triangle. Use a protractor to measure these angles.
Repeat steps 1-4 with a smaller isosceles triangle on the second sheet of paper. The smaller triangle should have a base of at least 10 cm and two sides of equal length.
Compare the measurements of the angles of both triangles. If the triangles are truly isosceles, then the two angles opposite the base (ACB) should measure the same in both triangles.
Cut out both isosceles triangles along their outlines.
Fold each triangle along the perpendicular bisector line drawn in step 3 so that the two congruent segments come together.
If the angles opposite the base are indeed equal, then the two sides of each triangle should match up perfectly when folded along the perpendicular bisector. If they do not match up, then the triangles are not truly isosceles.
By repeating this experiment with different sized isosceles triangles, we can verify that the base angles of any isosceles triangle are always equal.
Marrisa sold a total of 18,200 worth of clothing last week at her store.If her commision is 4% of sales,how much commisssion did she earn?
Answers
Answer:
She would earn 728 $ in commission
Step-by-step explanation:
help me get this right.

Answers
Answer:
A. 5/2
Step-by-step explanation:
Can't be c or d since those are negative and b would have a much steeper slope rise over run is how you find side the two points connect by going up 5 and over 2
9. Determine the discriminant of 2x² - 6x + 7 = 0 and then state how many solutions there are; additionally,
state the nature of the solutions. Do not solve.
Answers
We need to find the nature of the roots of the quadratic equation 2x² - 6x + 7 = 0 , and need to find the Discriminant
Now ,as we know that the Discriminant of any quadratic equation of the form ax² + bx + c = 0 , is D = b² - 4ac
So now ;
\({:\implies \quad \sf D=(-6)^{2}-4\times 2\times 7}\)
\({:\implies \quad \sf D=36-56}\)
\({:\implies \quad \bf \therefore \quad \underline{\underline{Discriminant=-20}}}\)
Now , as D < 0 ,So nature of roots will be imaginary
Guys can you please help. I dont understand. Thank you. :))))
Lines AB and CD intersect at E. If the measure of angle AEC=5x-20 and the measure of angle BED=x+50, find, in degrees, the measure of angle CEB.
Answers
Answer: 112.5
Step-by-step explanation: When line AB and CD intersect at point E, angle AEC equals BED so you set them equal to each other and find what x is. 5x -20 = x + 50, solving for x, which gives you 17.5. Finding x will tell you what AEC and BED by plugging it in which is 67.5. Angle BED and BEC are supplementary angles which adds up to 180 degrees. So to find angle CEB, subtract 67.5 from 180 and you get 112.5 degrees.
Find the area of this parallelogram.
12 inches
6 in.
7 in.
A. 42 inches
В.
42 square inches
O
C. 84 square inches
D. 72 square inches
O E. 72 inches
Answers
Answer:
it will be c
Step-by-step explanation:
¿Qué numero es mayor que -5/4?
-3/2
-1
-2
-3/4
Otros: me escriben cuál es
Answers
Answer:
10 /8es una fracción equivalente a5/4 15/12 y multiplica el número por un mis mo número y te saldrán infinitoss
Answer:
3/4 es mayor que -5/4 ..........
Professor Smith has a total of 250 students,
3/5
of whom are female. If x represents the number of female students, which of the following could be used to find the value of x?
Answers
Answer:
3.5=x/250
Step-by-step explanation:
The number of female students are 150.
Given that, professor Smith has a total of 250 students, 3/5 of whom are female.
What is an equation?In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =.
Here, x represents the number of female students.
Now, x= 3/5 × 250
⇒ x = 3 × 50
⇒ x = 150
Therefore, the number of female students are 150.
To learn more about an equation visit:
https://brainly.com/question/14686792.
#SPJ2
A pizza maker determined an annual profit in dollars
2
from selling pizzas using f(n) = 65n -0.04n² where
n is the number of pizzas sold. What is the annual
profit if the pizza maker sells 300 pizzas?
A. $18,500
B. $3,600
C. $7,800
D. $15,900
Answers
Answer:
Given, the annual profit equation is f(n) = 65n - 0.04n².
When the number of pizzas sold, n = 300, the annual profit will be:
f(300) = 65(300) - 0.04(300)²
= 19500 - 0.04(90000)
= 19500 - 3600
= $15,900
Therefore, the annual profit if the pizza maker sells 300 pizzas is $15,900. Answer: D.
Step-by-step explanation:
Can an empty set be a universal set?
Answers
Answer:
The empty set is defined as the complement of the universal set. That means where Universal set consists of a set of all elements, the empty set contains no elements of the subsets. The empty set is also called a Null set and is denoted by '{}'.
HOPE IT HELP YOU!
Answer:
The empty set is defined as the complement of the universal set. That means where Universal set consists of a set of all elements.
10x10x10 as a product of the same factor
Answers
Answer:
10^3
Step-by-step explanation
10 to the factor of 3
aka
10*10*10
PLEASE HELP ASAP WILL MARK BRAINLIEST
Part A
Which line best fits the data, l, m, or n? Why?
Part B
In the equation of a line, y = mx + b, what does b stand for? What is the value of b for the line of best fit?
Part C
In the equation of a line, y = mx + b , what does m stand for? What is the value of m for the line of best fit?
Part D
Now that you know m and b, what is the equation of the line of best fit?

Answers
Answer:
Part A:
Most of the data points are above line m. All of the data points are below line n. The data points are evenly distributed on either side of line l. Therefore, line l is the line of best fit for the data.
Part B:
For the line of best fit, the y-intercept is approximately 10 and the slope is approximately 2 .
Part C:
Y= 2x+10
Step-by-step explanation:
Part A:
Most of the data points are above line m. All of the data points are below line n. The data points are evenly distributed on either side of line l. Therefore, line l is the line of best fit for the data.
Part B:
To find the y-intercept of a line, identify where the line intersects the y-axis. Because the line of best fit is line l, the y-intercept is 10.
To find the slope, choose two points on line l, such as (10,30) and (30,70):
Part C:
To get the equation of the line, substitute the y-intercept, 10, for b and the slope, 2, for m.
Please give me the brainlliest crown Pls
Drag the tiles to the correct boxes to complete the pairs. Match the systems of equations with their solutions.
Answers
Answer:
See explanation for matching pairs
Step-by-step explanation:
Equations
(1)
\(x - y = 25\)
\(2x + 3y = 180\)
(2)
\(2x - 3y = -5\)
\(11x + y = 550\)
(3)
\(x - y = 19\)
\(-12x + y = 168\)
Solutions
\((-17,-36)\)
\((47, 33)\)
\((51, 26)\)
Required
Match equations with solutions
(1) \(x - y = 25\) and \(2x + 3y = 180\)
Make x the subject in: \(x - y = 25\)
\(x = 25 + y\)
Substitute \(x = 25 + y\) in \(2x + 3y = 180\)
\(2(25 + y) + 3y = 180\)
\(50 + 2y + 3y = 180\)
\(50 + 5y = 180\)
Collect like terms
\(5y = 180-50\)
\(5y = 130\)
Solve for y
\(y =26\)
Recall that: \(x = 25 + y\)
\(x = 25 + 26\)
\(x = 51\)
So:
\((x,y) = (51,26)\)
(2) \(2x - 3y = -5\) and \(11x + y = 550\)
Make y the subject in \(11x + y = 550\)
\(y = 550 - 11x\)
Substitute \(y = 550 - 11x\) in \(2x - 3y = -5\)
\(2x - 3(550 - 11x) = -5\)
\(2x - 1650 + 33x = -5\)
Collect like terms
\(2x + 33x = -5+1650\)
\(35x = 1645\)
Solve for x
\(x = 47\)
Solve for y in \(y = 550 - 11x\)
\(y = 550 - 11 * 47\)
\(y = 550 - 517\)
\(y = 33\)
So:
\((x,y) = (47,33)\)
(3)
\(x - y = 19\) and \(-12x + y = 168\)
Make y the subject in \(-12x + y = 168\)
\(y = 168 + 12x\)
Substitute \(y = 168 + 12x\) in \(x - y = 19\)
\(x - 168 - 12x = 19\)
Collect like terms
\(x -12x = 168 + 19\)
\(-11x = 187\)
Solve for x
\(x = -17\)
Solve for y in \(y = 168 + 12x\)
\(y =168-12 *17\)
\(y =-36\)
So:
\((x,y) = (-17,-36)\)
The Central Limit Theorem can also be used to investigate unusual events. An unusual event is one that occurs with a probability of less than ___%
Answers
The Central Limit Theorem can also be used to investigate unusual events. An unusual event is one that occurs with a probability of less than 1%
The Central Limit Theorem can be used to investigate unusual events by calculating the probability of a sample mean being a certain number of standard deviations away from the population mean.
If we assume that the population is normally distributed, then we can use the normal distribution to calculate the probability of observing a sample mean that is a certain number of standard deviations away from the population mean.
An unusual event is typically defined as an event that occurs with a low probability, usually less than 5% or 1%. So, if we observe a sample mean that is more than 2 standard deviations away from the population mean, we can say that this is an unusual event that occurs with a probability of less than 5%. Similarly, if we observe a sample mean that is more than 3 standard deviations away from the population mean, we can say that this is an unusual event that occurs with a probability of less than 1%.
Learn more about Central Limit Theorem here
brainly.com/question/18403552
#SPJ4
Sam walks 100 m north and then 100 m east. How far is she from her starting position? Give your answer to a sensible degree of accuracy.
Answers
Answer- 200m
: Right now Sam is 200m far from her starting point

__________ refer to the probabilities of the states of nature after revising the prior probabilities based on sample information.
Answers
The probabilities of the states of nature after revising the prior probabilities based on sample information are called posterior probabilities.
The concept of posterior probabilities is fundamental in Bayesian statistics, which is a branch of statistics that deals with probability distributions of parameters based on prior knowledge and observed data. In Bayesian statistics, the prior probability represents the degree of belief in a hypothesis before new data is collected. The posterior probability, on the other hand, represents the updated degree of belief in the hypothesis after new data is collected.
The posterior probability is calculated using Bayes' theorem, which relates the conditional probabilities of the hypothesis and the data. The formula for Bayes' theorem is:
posterior probability = (prior probability x likelihood) / evid
The likelihood represents the probability of observing the data given the hypothesis, while the evidence is a normalizing constant that ensures the posterior probability integrates to one.
for such more question on posterior probabilities.
https://brainly.com/question/13604758
#SPJ11
the intensity in the interference pattern of n identical slits is given by i=i0[sin(nϕ/2)sin(ϕ/2)]2.
Answers
The intensity in the interference pattern of n identical slits is given by the formula:
I = I₀ [sin(nϕ/2) sin(ϕ/2)]²
Here's a step-by-step explanation of the terms in this formula:
1. I is the intensity at a point in the interference pattern.
2. I₀ is the maximum intensity at the center of the pattern (i.e., when ϕ = 0).
3. n is the number of identical slits.
4. ϕ is the phase difference between the waves from adjacent slits at the point being considered.
To find the intensity at a specific point in the interference pattern, you need to know the values of I₀, n, and ϕ. Then, you can simply plug these values into the formula and calculate the intensity I.
To learn more about Intensity
https://brainly.com/question/16241795
#SPJ11
rectangle m is similar to rectangle n. which scale factor was used to dilate rectangle M rectangle n

Answers
we know that
If two figures are similar, then the ratio of its corresponding sides is proportional
and this ratio is called the scale factor
so
In this problem
scale factor =12/18
Simplify
=6/9
=2/3
therefore
the answer is option C
mr. patrick teaches math to 15 students. he was grading tests and found that when he graded everyone's test except payton's, the average grade for the class was 80. after he graded payton's test, the class average became 81. what was payton's score on the test?
Answers
Mr. Patrick instructs 15 students in math. He discovered that Payton had received a 95 on the test while grading them from average.
There are 15 kids in Mr. Patrick's class. The average score on his most recent exam was 80 for 14 candidates (not including Payton).
I'm going to use x to represent the unknowable sum of the 14 test scores. Average is computed by adding all the numbers in the set (whose average you're trying to get) together, then dividing by the total number of numbers in that set.
This was the total of their scores: x=1120.
Adding Payton's score now (I'll use the letter p to stand in for her score):
1120+p /15=81→ Her test score was included in the fifteen students' average, which was 81 1120+p=1215
P=95.
Learn more about average here
https://brainly.com/question/12322912
#SPJ4
8. The graph is of a function in the form p(t) = a • bt. What is the function? (2 points
9. Use this function to estimate the boa constrictor population in 2 years, 3 years, and 4 years. (6 points: 2 points for each year, including 1 point for showing your work and 1 point for the answer)
t: Time in years
P(t): Estimated snake population at time t
2
3
4
10. What pattern do you see in years 2, 3, and 4? How is the snake population changing every year? (2 points
11. How is the snake population changing every two years? (1 point
Making a Decision:
12. Do you think the snake population can continue to grow in this way forever? Why or why not? (2 points)

Answers
9514 1404 393
Answer:
8. p(t) = 5(2^t)
9. 20, 40, 80
10. doubles every year
11. multiplies by 4
12. no, it will soon exceed available habitat
Step-by-step explanation:
8. From the graph, a = p(0) = 5, and b = p(1)/p(0) = 10/5 = 2.
The function is ...
p(t) = 5(2^t)
__
9. You can read the values from the graph: 2 years: 20; 3 years: 40; 4 years: 80.
If you insist on evaluating the function, you have ...
p(2) = 5(2^2) = 5·4 = 20
p(3) = 5(2^3) = 5·8 = 40
p(4) = 5(2^4) = 5·16 = 80
__
10. The population doubles each year.
__
11. In 2 years, the population doubles twice, so is multiplied by 4.
__
12. No. Exponential functions don't last long in the real world. Eventually, required resources run out. In 15 years, there would be 163,840 snakes; in 20 years, there would be 5.2 million snakes; in 40 years, there would be 5.5 trillion snakes, about 44 snakes for every acre of land on earth (including polar areas).
You please help me with the second part i need it to pass this by friday

Answers
The inequality formed is x + 6 > 20 and Julie will sell more than 14 items after the first Week
What is inequality ?A relationship between two expressions or values that is not equal to one another is referred to as "inequality" in mathematics.
According to the given information
Let x be the more items that Julie will sell after First week
Number of items soled in First week = 6
So
The inequality formed will be
x + 6 > 20
Solving the inequality is
x > 20 - 6
x > 14
So
The inequality formed is x + 6 > 20 and Julie will sell more than 14 items after the first Week
To know more about Inequality
https://brainly.com/question/29166625
#SPJ1
Suppose a simple random sample of five hospitals is to be drawn from a population of 20 hospitals. There are 15,504 different samples of size 5 that can be drawn. The relative frequency distribution of the values of the mean of these 15,504 different samples would specify the ________ of the mean. Group of answer choices sampling distribution confidence level confidence interval normal distribution
Answers
The relative frequency distribution of the values of the mean of these 15,504 different samples would specify the sampling distribution of the mean.
What does the relative frequency distribution of the values of the mean of the 15,504 different samples specify?The sampling distribution of the mean refers to the distribution of sample means obtained from repeated sampling from the same population.
In this case, we have 15,504 different samples of size 5 drawn from a population of 20 hospitals.
Each sample has its own sample mean. The relative frequency distribution of these sample means would specify the sampling distribution of the mean.
The sampling distribution of the mean is important in statistics because it allows us to make inferences about the population mean based on the distribution of sample means.
It helps us understand the variability of sample means and provides a basis for constructing confidence intervals and conducting hypothesis tests.
Therefore, the relative frequency distribution of the mean values from the different samples would describe the characteristics of the sampling distribution of the mean..
Learn more about sampling distribution
brainly.com/question/31465269
#SPJ11
Solve the equation-
\( \frac{5}{x - 3} - \frac{4}{x + 4} = \frac{1}{x} \)
Answers
Hello studentUnion!
\( \huge \boxed{\mathfrak{Question} \downarrow}\)
Solve the equation-
\( \frac{5}{x - 3} - \frac{4}{x + 4} = \frac{1}{x} \\ \)
\( \large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}\)
\( \frac{5}{x - 3} - \frac{4}{x + 4} = \frac{1}{x} \\ \)
Let's multiply both the sides of the equation by x (x - 3) & (x + 4) which is the LCM of (x - 3), (x + 4) & x. We can't solve it directly without taking the LCM first as the denominators are not equal to each other. Then do cross multiplication. After all these steps, you'll get an equation as..
\(x\left(x+4\right)\times 5-x\left(x-3\right)\times 4=\left(x-3\right)\left(x+4\right) \\ \)
Now, use the distributive property & simplify it.
\(x\left(x+4\right)\times 5-x\left(x-3\right)\times 4=\left(x-3\right)\left(x+4\right) \\ \left(x^{2}+4x\right)\times 5-x\left(x-3\right)\times 4=\left(x-3\right)\left(x+4\right) \\ 5x^{2}+20x-x\left(x-3\right)\times 4=\left(x-3\right)\left(x+4\right) \\ 5x^{2}+20x-\left(x^{2}-3x\right)\times 4=\left(x-3\right)\left(x+4\right) \\ 5x^{2}+20x-\left(4x^{2}-12x\right)=\left(x-3\right)\left(x+4\right) \\ 5x^{2}+20x-4x^{2}+12x=\left(x-3\right)\left(x+4\right) \\ x^{2}+20x+12x=\left(x-3\right)\left(x+4\right) \\ x^{2}+32x=\left(x-3\right)\left(x+4\right) \\ x^{2}+32x=x^{2}+x-12 \\ x^{2}+32x-x^{2}=x-12 \\ 32x=x-12 \\ 32x-x=-12 \\ 31x=-12 \\ \boxed{ \boxed{ \bf \: x=-\frac{12}{31} }}\)
The value of x is -12/31.__________________
Hope it'll help you!
ℓu¢αzz ッ
Answer:
\(\frac{5}{x-3} -\frac{4}{x+4} =\frac{1}{x}\)
\(\frac{5(x+4)-4(x-3)}{(x-3)(x+4)} =\frac{1}{x} \\\)
\(\frac{5x+20-4x+12}{(x-3)(x+4)} =\frac{1}{x}\)
\(\frac{x+32}{(x-3)(x+4)} =\frac{1}{x}\)
Use Cross multiplication
\(x(x+32)=(x-3)(x+4)\)
\(x^{2} +32x = x^{2} +4x-3x-12\)
\(x^{2} +32x=x^{2} +x-12\)
\(x^{2} +32x-x^{2} -x=-12\)
\(31x = -12\)
\(\frac{31x}{31} =\frac{-12}{31} \\x = \frac{-12}{31}\)
Hope this helps you.
Let me know if you have any other questions :-)
The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.

Answers
Answer:
y=40°
Z + Y = 70°
z. = 70°-40°
z. = 30°
POH=X
=180-70
=110°
maximize B=5xy^2 where x and y are positive numbers such that x+y^2=8
the Max value of B is ?
Answers
The maximum value of B is 80.
1. We are given the expression B = 5xy² and the constraint x + y² = 8.
2. We need to find the maximum value of B by optimizing the variables x and y.
3. To solve this problem, we can use the method of Lagrange multipliers.
4. Let's define the Lagrange function L(x, y, λ) as L(x, y, λ) = B - λ(x + y² - 8).
5. Taking the partial derivatives of L concerning x, y, and λ, we have:
∂L/∂x = 5y² - λ
∂L/∂y = 10xy - 2λy
∂L/∂λ = -(x + y² - 8)
6. Setting the partial derivatives equal to zero, we get the following equations:
5y² - λ = 0 ...(1)
10xy - 2λy = 0 ...(2)
x + y² = 8 ...(3)
7. From equation (1), we can solve for λ in terms of y:
λ = 5y² ...(4)
8. Substituting equation (4) into equation (2), we have:
10xy - 2(5y²)y = 0
10xy - 10y³ = 0
10y(x - y²) = 0
9. From the above equation, we have two possibilities:
i) 10y = 0, which implies y = 0.
ii) x - y² = 0, which implies x = y².
10. If y = 0, then from equation (3), we get x = 8.
11. If x = y², then substituting this into equation (3), we have:
y² + y² = 8
2y² = 8
y² = 4
y = ±2
If y = 2, then x = (2)² = 4.
If y = -2, then x = (-2)² = 4.
12. We have three potential solutions: (x, y) = (8, 0), (4, 2), and (4, -2).
13. Finally, substitute each of these solutions into the expression B = 5xy² and find the maximum value of B:
B = 5(8)(0)² = 0
B = 5(4)(2)² = 80
B = 5(4)(-2)² = 80
14. Therefore, the maximum value of B is 80.
For more such questions on value, click on:
https://brainly.com/question/843074
#SPJ8
Complete the statement ABC~ ? By which postulate or
theorem are the triangles similar?
A) AKN; SSS~ C) ANK; SAS~
B) AKN; SAS~ D) ANK; AA~
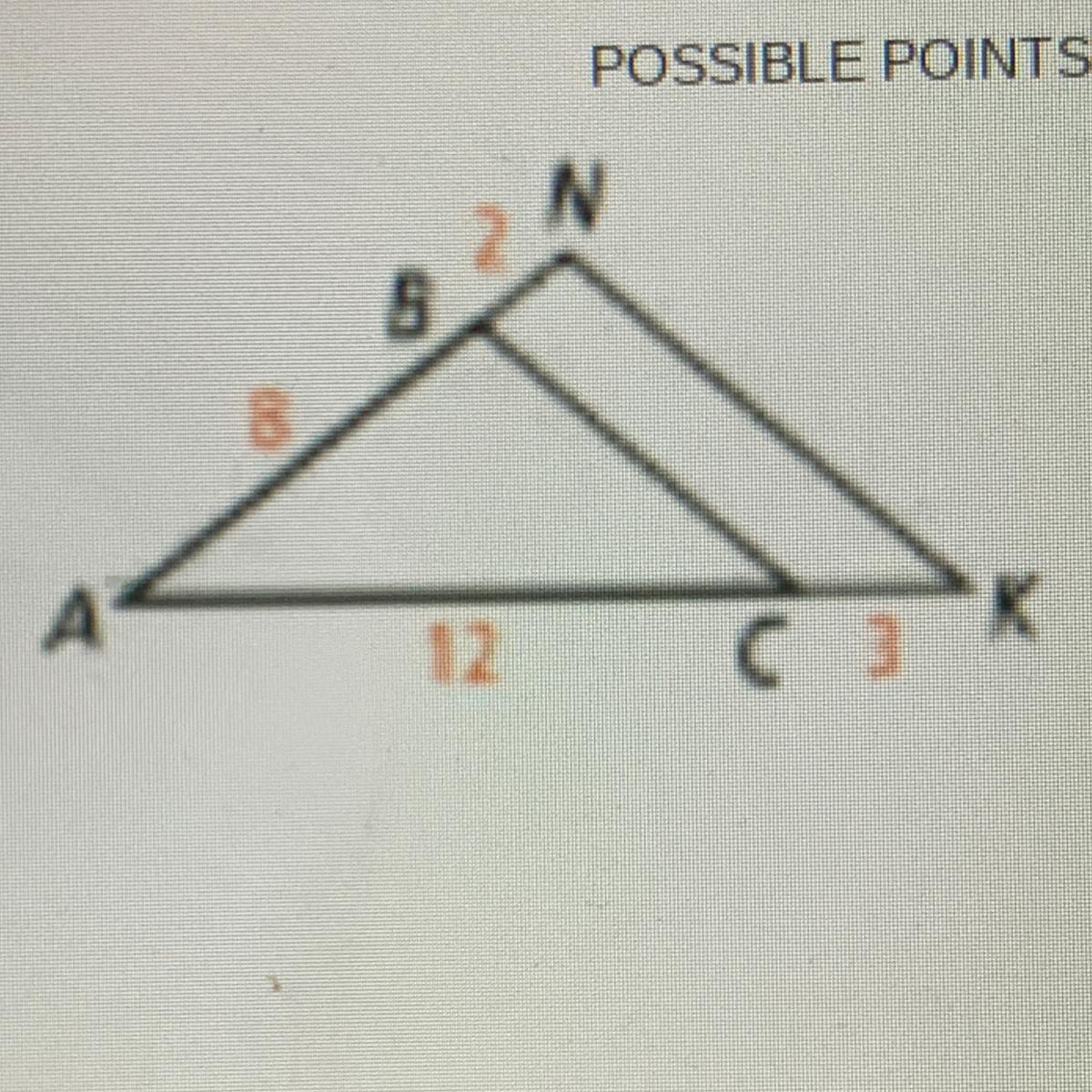
Answers
Answer:
option b is the correct answer I am expecting