Determine the x- and y- intercepts for the graph defined by the given equation. x = -9 Please select the best answer from the choices provided

Answers
x intercept when y = 0, the x intercept would always be -9
Vertical line, does not have y intercept
Solution: A
Related Questions
A ferry traveled 1/2 of the distance between two ports in 3/4 hour. The ferry travels at a constant rate. At this rate, what fraction of the distance between the two ports can the ferry travel in one hour?
Answers
Answer:
Division!
Step-by-step explanation:
(1/6) ÷ (3/7)
(1/6)(7/3)
= 7 / 18
solve the inequality
14 > 0.6 x 14
Answers
How many pivot columns must A have if its columns span R5? Why? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The matrix must have pivot columns. If A had fewer pivot columns, then the equation Ax = 0 would have only the trivial solution. B. The matrix must have pivot columns. The statements "A has a pivot position in every row" and "the columns of A span R5" are logically equivalent. C. The matrix must have pivot columns. Otherwise, the equation Ax = 0 would have a free variable, in which case the columns of A would not span R5. D. The columns of a 5x7 matrix cannot span R5 because having more columns than rows makes the columns of the matrix dependent.
Answers
The matrix must have pivot columns. Otherwise, the equation Ax = 0 would have a free variable, in which case the columns of A would not span R5. Therefore, the correct answer is C.
A pivot column is a column of the matrix that has a non-zero entry in the pivot position and all entries below the pivot are zero. In row echelon form, every row below a pivot column has a zero in the corresponding position. The pivot columns correspond to the linearly independent columns of the original matrix and the number of pivot columns determines the rank of the matrix.
The rank of a matrix is defined as the number of linearly independent columns or rows in the matrix. If the columns of a matrix span Rn, then the rank of the matrix must be equal to n. This means that the matrix must have n linearly independent columns. To ensure that the columns of A span R5, A must have at least 5 pivot columns. If A had fewer pivot columns, then the equation Ax = 0 would have a non-trivial solution, meaning that the columns of A would not be linearly independent and would not span R5.
You can learn more about pivot column at
https://brainly.com/question/29786913
#SPJ4
What is the y-intercept in the equation y = 45x + 65?

Answers
Answer:
The y intercept is : 65
Step-by-step explanation:
The y intercept is 65 as it is in the form of y=mx+c.
The c is the y intercept, being 65
A relationship between two quantities, normally expressed as the quotient of one divided by another. A comparison of two numbers or measurements.
Answers
The relationship that is normally expressed as the quotient of one quantity divided by another is called a ratio
The relationship that is normally expressed as the quotient of one quantity divided by another is called a ratio. A ratio is a comparison of two numbers or measurements, and it can be written in different ways.
For example, if we have two quantities A and B, the ratio of A to B can be written as
A/B
A:B
"A is to B"
The ratio of A to B tells us how many times A is contained within B, or how many units of A we would need to have to match the amount of B.
Ratios are useful in many fields, such as finance, engineering, and science, where they are used to compare and analyze different quantities and their relationships.
Learn more about ratio here
brainly.com/question/23499990
#SPJ4
As you radio the hospital to give a report on your patient, which of the following should you do? Provide as much detail as possible. Use code words to protect the patient's identity. Speak as quickly as possible. Remain objective and impartial.
Answers
When radioing the hospital to give a report on a patient, it is important to use code words to protect the patient's identity, remain objective and impartial, and provide as much detail as possible.
It is not necessary to speak quickly, as clear and accurate communication is more important than speed. Providing detailed information about the patient's condition, including vital signs and any treatment administered, will help the hospital staff prepare for the patient's arrival and provide appropriate care. Additionally, it is important to maintain patient confidentiality and avoid disclosing any identifying information that could potentially compromise the patient's privacy.
Learn more about Confidentiality here:
https://brainly.com/question/863709
#SPJ4
PLZZ HURRY NO LINKS!!!! Joseph attends a school that has 800 students. He is in charge of school dances this year. He surveyed a random sample of 100 students and got the following feedback.
710
of the students would attend any of the dances held at the school
25
of the students would like to have pizza served at the dances
410
of the students would attend a square dance
64% of the students think that the dances should be held after football games
18% of the students are not allowed to attend dances at school
Which THREE statements are supported by Joseph's data?
A
Out of 800 students, Joseph could expect around 480 students to attend a square dance.
B
Joseph should plan for around 560 students at each dance based on the data.
C
Joseph found that no more than 320 students would want pizza at the school dance.
D
Out of the 800 students, 288 do not like to attend dances after the football games.
E
The dances will be attended by around 700 of the students that attend the schoo
Answers
Answer: I got answers A, B and E
Step-by-step explanation:
The correct three statements are supported by Joseph's data are as follows;
Joseph should plan for around 560 students at each dance based on the data.
The dances will be attended by around 700 of the students that attend the school.
Out of the 800 students, 288 do not like to attend dances after the football games.
What is the data set?A data set is a collection of numbers or values that relate to a particular subject.
Joseph attends a school that has 800 students. He is in charge of school dances this year.
He surveyed a random sample of 100 students and got the following feedback.
7/10 of the students would attend any of the dances held at the school.2/5 of the students would like to have pizza served at the dances.4/10 of the students would attend a square dance.64% of the students think that the dances should be held after football games.18% of the students are not allowed to attend dances at school.1. Here 7/10 of the students would attend any of the dances held at the school.
\(=\dfrac{ 7}{10}\times 800\\\\= 7 \times 80\\\\= 560\)
Joseph should plan for around 560 students at each dance based on the data.
2. 18% of the students are not allowed to attend dances at school.
\(= (1-0.18)\times 800\\\\= 0.82 \times 800\\\\=656\)
The dances will be attended by around 700 of the students that attend the school.
3. 64% of the students think that the dances should be held after football games.
\(=(1-0.64 )\times 800\\\\= 0.36 \times 800\\\\=288\)
Out of the 800 students, 288 do not like to attend dances after the football games.
Learn more about data set here;
https://brainly.com/question/15128975
#SPJ2
the number of hours per week that the television is turned on is determined for each family in a sample. the mean of the data is 34 hours and the median is 30.2 hours. twenty-four of the families in the sample turned on the television for 19 hours or less for the week. the 8th percentile of the data is 19 hours.step 2 of 5: approximately how many families are in the sample? round your answer to the nearest integer.
Answers
Any families that watched less than 10 hours or more than 58 hours (i.e., mean ± 2 standard deviations) could be considered outliers.
To estimate the number of families in the s(ample, we need more information about the data. We know that 24 families turned on the television for 19 hours or less but we don't know the total number of families in the sample.
One possible approach is to use the median and interquartile range (IQR) to estimate the sample size. The IQR is the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of the data. Since the median is 30.2 hours, we can assume that half of the families watched more than 30.2 hours and half watched less. Therefore, the median is equivalent to the 50th percentile (Q2).
Using this information, we can estimate that Q1 is around 22 hours (since Q1 to Q2 is half the range of data), and Q3 is around 46 hours (since Q2 to Q3 is also half the range). The IQR is then 46 - 22 = 24 hours.
We can use the IQR to estimate the spread of the data and identify any outliers. If we assume that the data follows a normal distribution, we can use the rule of thumb that states that about 50% of the data falls within one standard deviation of the mean. Since the mean is 34 hours and the IQR is 24 hours, we can estimate that one standard deviation is around 12 hours. Therefore, any families that watched less than 10 hours or more than 58 hours (i.e., mean ± 2 standard deviations) could be considered outliers.
Based on this analysis, we can estimate that there are around 48 families in the sample (assuming a symmetric distribution). However, this is just a rough estimate and may not be accurate without more information about the data.
Learn more about data brainly.com/question/30051017
#SPJ11
If you don’t no do not comment

Answers
Answer: number three the answer is 0.15 And for number four the answer is 0.49, 0.5, 3/5, 17/20
Step-by-step explanation:
Can anyone explain why the answer is B? Tyyy

Answers
Answer:
B. 4.09 cm²
Step-by-step explanation:
Let point O be the center of the circle.
As the center of the circle is the midpoint of the diameter, place point O midway between P and R.
Therefore, line segments OP and OQ are the radii of the circle.
As the radius (r) of a circle is half its diameter, r = OP = OQ = 5 cm.
As OP = OQ, triangle POQ is an isosceles triangle, where its apex angle is the central angle θ.
To calculate the shaded area, we need to subtract the area of the isosceles triangle POQ from the area of the sector of the circle POQ.
To do this, we first need to find the measure of angle θ by using the chord length formula:
\(\boxed{\begin{minipage}{5.8 cm}\underline{Chord length formula}\\\\Chord length $=2r\sin\left(\dfrac{\theta}{2}\right)$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the central angle.\\\end{minipage}}\)
Given the radius is 5 cm and the chord length PQ is 6 cm.
\(\begin{aligned}\textsf{Chord length}&=2r\sin\left(\dfrac{\theta}{2}\right)\\\\\implies 6&=2(5)\sin \left(\dfrac{\theta}{2}\right)\\\\6&=10\sin \left(\dfrac{\theta}{2}\right)\\\\\dfrac{3}{5}&=\sin \left(\dfrac{\theta}{2}\right)\\\\\dfrac{\theta}{2}&=\sin^{-1} \left(\dfrac{3}{5}\right)\\\\\theta&=2\sin^{-1} \left(\dfrac{3}{5}\right)\\\\\theta&=73.73979529...^{\circ}\end{aligned}\)
Therefore, the measure of angle θ is 73.73979529...°.
Next, we need to find the area of the sector POQ.
To do this, use the formula for the area of a sector.
\(\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\left(\dfrac{\theta}{360^{\circ}}\right) \pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in degrees.\\\end{minipage}}\)
Substitute θ = 73.73979529...° and r = 5 into the formula:
\(\begin{aligned}\textsf{Area of section $POQ$}&=\left(\dfrac{73.73979529...^{\circ}}{360^{\circ}}\right) \pi (5)^2\\\\&=0.20483... \cdot 25\pi\\\\&=16.0875277...\; \sf cm^2\end{aligned}\)
Therefore, the area of sector POQ is 16.0875277... cm².
Now we need to find the area of the isosceles triangle POQ.
To do this, we can use the area of an isosceles triangle formula.
\(\boxed{\begin{minipage}{6.7 cm}\underline{Area of an isosceles triangle}\\\\$A=\dfrac{1}{2}b\sqrt{a^2-\dfrac{b^2}{4}}$\\\\where:\\ \phantom{ww}$\bullet$ $a$ is the leg (congruent sides). \\ \phantom{ww}$\bullet$ $b$ is the base (side opposite the apex).\\\end{minipage}}\)
The base of triangle POQ is the chord, so b = 6 cm.
The legs are the radii of the circle, so a = 5 cm.
Substitute these values into the formula:
\(\begin{aligned}\textsf{Area of $\triangle POQ$}&=\dfrac{1}{2}(6)\sqrt{5^2-\dfrac{6^2}{4}}\\\\ &=3\sqrt{25-9}\\\\&=3\sqrt{16}\\\\&=3\cdot 4\\\\&=12\; \sf cm^2\end{aligned}\)
So the area of the isosceles triangle POQ is 12 cm².
Finally, to calculate the shaded area, subtract the area of the isosceles triangle from the area of the sector:
\(\begin{aligned}\textsf{Shaded area}&=\textsf{Area of sector $POQ$}-\textsf{Area of $\triangle POQ$}\\\\&=16.0875277...-12\\\\&=4.0875277...\\\\&=4.09\; \sf cm^2\end{aligned}\)
Therefore, the area of the shaded region is 4.09 cm².

Need help solving! I got 4x+17 with a remainder of 42 not sure if it is correct!

Answers
Given:
\(\frac{4x^2+5x-9}{x-3}\)Using synthetic division we get,
Hence, the answer is,
\(4x+17+\frac{42}{x-3}\)
HELP ASAP PLZ!!!!!!!!
Solve this problem.
b - 6 < 4
Answers
Hi!
Your answer would be: 3(or 4, or 5)
but the main answer is 3.
Hope this helps!
Sadie is doing weekly payroll for her employees at her car dealership. Her employees make a base salary plus commission. The function LaTeX: E(x)=\mid 5- \frac{6x}{2}\mid models the way Sadie calculates the commission where x represents the number of cars the employee sells. If one of her employees sells 7 cars, how much commission will they make?
Answers
The commission function is an illustration of the absolute functions
The commission for the sales of 7 cars is 16
The function is given as:
\(\mathbf{E(x)=\mid 5- \frac{6x}{2}\mid}\)
When an employee sells 7 cars, we have:
x = 7
So, the equation becomes
\(\mathbf{E(x)=\mid 5- \frac{6\times 7}{2}\mid}\)
Simplify
\(\mathbf{E(x)=\mid 5- 3\times 7\mid}\)
\(\mathbf{E(x)=\mid 5- 21\mid}\)
Simplify
\(\mathbf{E(x)=\mid- 16\mid}\)
Remove absolute brackets
\(\mathbf{E(x) = 16}\)
Hence, the commission for the sales of 7 cars is 16
Read more about absolute functions at
https://brainly.com/question/1389494
Evaluate the expression when X equals three and Y equals negative one. Show your work. 5X plus 4Y over two
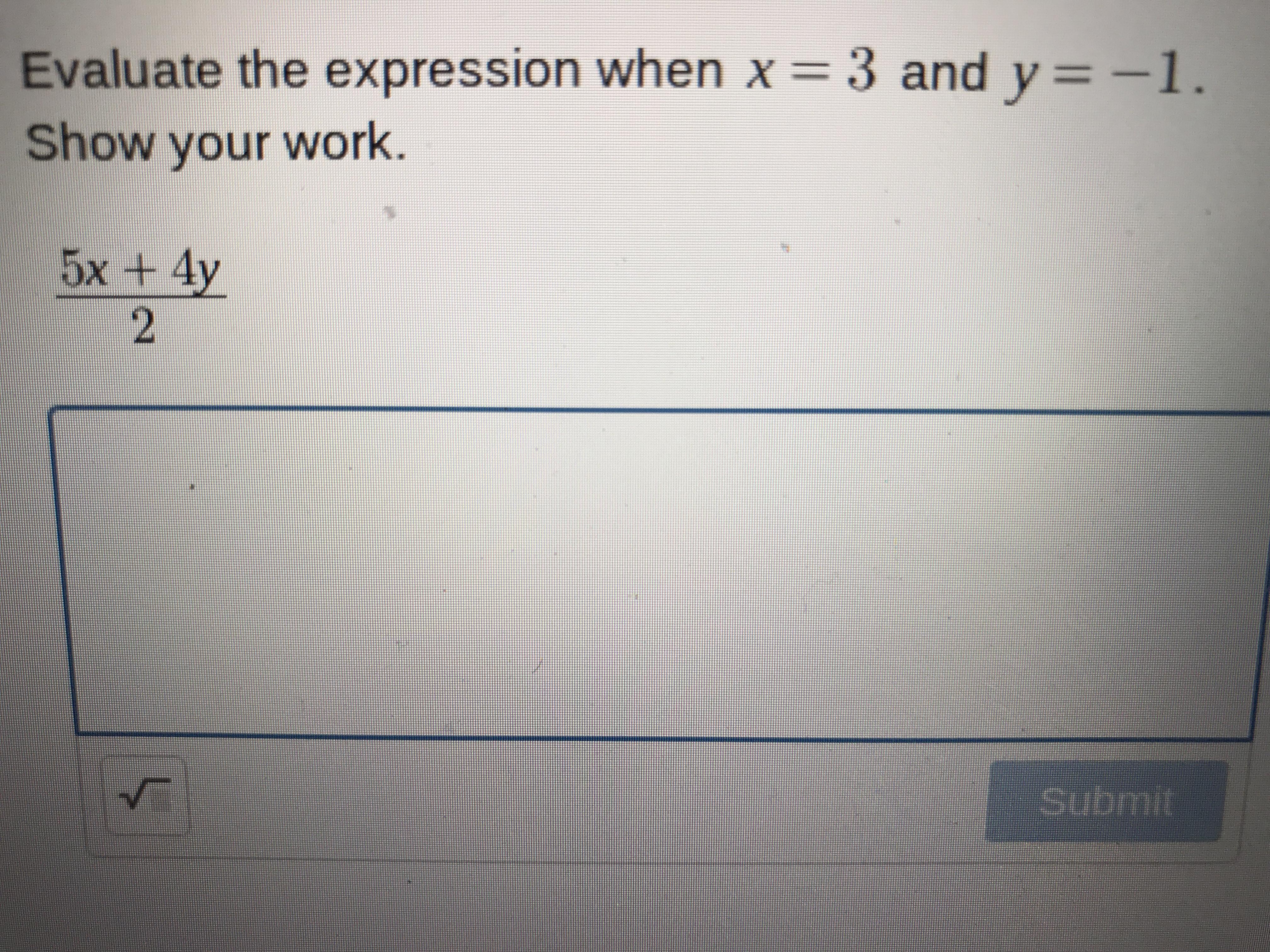
Answers
Answer:
11/2
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightStep-by-step explanation:
Step 1: Define
(5x + 4y)/2
x = 3
y = -1
Step 2: Evaluate
Substitute: (5(3) + 4(-1))/2Multiply: (15 - 4)/2Subtract: 11/2Answer:
\(\frac{11}{2}\)
Step-by-step explanation:
\(\frac{5x+4y}{2}\\=\frac{5(3)+4(-1)}{2}\\=\frac{15-4}{2}\\=\frac{11}{2}\)
Find the missing angle measure, arc measure of solve for x. Show all work!

Answers
Answer:
hmmmmm
Step-by-step explanation:
Answer:
m∠SRT = 47°
Step-by-step explanation:
The measure of an inscribed angle is 1/2 the measure of the intercepted arc.
So,
16x - 1 = 1/2(30x + 4) = 15x + 2
x - 1 = 2
x = 3
m∠SRT = 16(3) - 1 = 48 - 1 = 47
The function f(x)
ƒ(x) = ( 2/5)x is shown on the coordinate plane. Which statement
is true?

Answers
In the right end, as x increases without bound, the graph of f(x) decreases.
In the left end, as x decreases without bound, the graph of f(x) increases.
How is this shown on the graph?The graph shows that the function has a decreasing end behavior without bound.
This means that as x increases, f(x) decreases indefinitely. The arrow on the graph indicates this trend, as the function extends without limit.
The graph clearly illustrates that as x increases, f(x) approaches the x-axis. Therefore, it can be concluded that the function approaches negative infinity as x approaches infinity.
Read more about graphs here:
https://brainly.com/question/26233943
#SPJ1
PLS HELP
Find the value of x in the triangle shown below

Answers
Answer:
62
Step-by-step explanation:
Answer:
x = 61.641°
Step-by-step explanation:
Hope it's help, study well and goodluck!!

It is 1.7 km from Carmen's house to the nearest mailbox. How far is it in meters?
Be sure to include the correct unit in your answer.
Answers
Answer:
1700 meters
Step-by-step explanation:
\(1 \: km \: = 1000 \: meters \\ 1.7 \: km = 1.7 \times 1000 = 1700 \: meters\)
need help asap pleaseee

Answers

Answer:
starting at (0, 8), each point is up 1 and right 4
Step-by-step explanation:
y- intercept is (0,8)
slope is 1/4
(4,9)
(8,10)
pls help if you can asap!!!!

Answers
Answer: x= 6
Step-by-step explanation:
Since the shape is a parallelogram, the angles will either be equal to each other or add up to 180.
You can see they do not look the same so they add up to equal 180
12x + 3 +105 = 180
12x + 108 = 180
12x = 72
x = 6
Solve the system by using a matrix equation.
--4x - 5y = -5
-6x - 8y = -2
Answers
Answer:
Solution : (15, - 11)
Step-by-step explanation:
We want to solve this problem using a matrix, so it would be wise to apply Gaussian elimination. Doing so we can start by writing out the matrix of the coefficients, and the solutions ( - 5 and - 2 ) --- ( 1 )
\(\begin{bmatrix}-4&-5&|&-5\\ -6&-8&|&-2\end{bmatrix}\)
Now let's begin by canceling the leading coefficient in each row, reaching row echelon form, as we desire --- ( 2 )
Row Echelon Form :
\(\begin{pmatrix}1\:&\:\cdots \:&\:b\:\\ 0\:&\ddots \:&\:\vdots \\ 0\:&\:0\:&\:1\end{pmatrix}\)
Step # 1 : Swap the first and second matrix rows,
\(\begin{pmatrix}-6&-8&-2\\ -4&-5&-5\end{pmatrix}\)
Step # 2 : Cancel leading coefficient in row 2 through \(R_2\:\leftarrow \:R_2-\frac{2}{3}\cdot \:R_1\),
\(\begin{pmatrix}-6&-8&-2\\ 0&\frac{1}{3}&-\frac{11}{3}\end{pmatrix}\)
Now we can continue canceling the leading coefficient in each row, and finally reach the following matrix.
\(\begin{bmatrix}1&0&|&15\\ 0&1&|&-11\end{bmatrix}\)
As you can see our solution is x = 15, y = - 11 or (15, - 11).
There are 25 pieces of candy in a bowl, and 15 of them are chocolate. What percentage of pieces of candy in the bowl are chocolate?
Answers
60% of the pieces of candy in the bowl are chocolate.
(15/25)*100 = 60%
suppose this system of linear differential equations can be put in the form . determine and . is the system homogeneous or nonhomogeneous? choose find the largest interval such that a unique solution of the initial value problem is guaranteed to ex
Answers
The system of linear differential equations is homogeneous and the largest interval such that a unique solution of the initial value problem is guaranteed to exist is (-∞, ∞).
Given the system of linear differential equations can be put in the form (A - λI)X = 0, where λ and X are the eigenvalue and eigenvector of the matrix A, respectively. Determine λ and X and determine whether the system is homogeneous or non-homogeneous. Choose the largest interval such that a unique solution of the initial value problem is guaranteed to exist.For the given system of linear differential equations:
dx/dt = 4x + 6y
dy/dt = -2x - 4y
the matrix A is given by:
[4 6 ][-2 -4 ]
The eigenvalue λ can be found from the characteristic equation det(A - λI) = 0 as follows:
[4 - λ 6 ][-2 -4 - λ] = 0λ² - λ - 8 = 0
Solving the above equation, we get, λ = -1 and λ = 8.
Therefore, λ1 = -1 and λ2 = 8 are the eigenvalues of matrix A.
To find the eigenvectors, we solve the equation (A - λI)X = 0 for each λ separately.
For λ1 = -1, we get[A - (-1)I]X = 0
⇒[5 6 ][x ] = 0[-2 -3][y ] [x ][-2y ]
Therefore, the eigenvector corresponding to
λ1 = -1 is
X1 = [x y]T = [2 -1]T.
For λ2 = 8, we get
[A - 8I]X = 0⇒[-4 6 ][x ]
= 0[-2 -12][y ] [x ][3y ]
Therefore, the eigenvector corresponding to
λ2 = 8 is
X2 = [x y]T = [3 1/2]T.
The given system of linear differential equations can be written in the matrix form as
dX/dt = AX,
where A is the matrix [4 6][-2 -4] and X is the column vector [x y]T.
The general solution of this system is given by
X(t) = c1 e^(λ1t)X1 + c2 e^(λ2t)X2,
where c1 and c2 are constants of integration and X1 and X2 are the eigenvectors corresponding to the eigenvalues λ1 and λ2, respectively. Therefore, the general solution of the given system is given by
x(t) = 2c1 e^(-t) + 3/2 c2 e^(8t)y(t)
= -c1 e^(-t) + 1/2 c2 e^(8t)
where c1 and c2 are constants of integration to be determined from the initial conditions. Since the system of differential equations is homogeneous, the trivial solution x(t) = y(t) = 0 is a solution of the system. Hence, the system is homogeneous.
The given initial value problem has initial conditions x(0) = 1 and y(0) = 0.
Therefore, we have
c1 + 3/2 c2 = 1 and
-c1 + 1/2 c2 = 0
Solving these two equations, we get c1 = 1/5 and c2 = 2/5.
Therefore, the particular solution of the given initial value problem is given by
x(t) = (2/5) e^(-t) + (6/5) e^(8t)y(t)
= -(1/5) e^(-t) + (1/5) e^(8t)
Hence, the largest interval such that a unique solution of the initial value problem is guaranteed to exist is (-∞, ∞).
The system of linear differential equations is homogeneous and the largest interval such that a unique solution of the initial value problem is guaranteed to exist is (-∞, ∞).
To know more about differential equations visit:
https://brainly.com/question/32645495
#SPJ11
531
x 47
Long multiplication :) please help
Answers
Greg has the following utility function: u = x038x962. He has an income of $83.00, and he faces these prices: (P1, P2) = (4.00, 1.00). Suppose that the price of x increases by $1.00. Calculate the compensating variation for this price change. Give your answer to two decimals.
Answers
The compensating variation is $13.52.
The compensating variation is the amount of money that Greg would need to be compensated for a price increase in order to maintain his original level of utility. In this case, Greg's utility function is u = x<sup>0.38</sup>x<sup>0.962</sup>. His income is $83.00, and he faces these prices: (P1, P2) = (4.00, 1.00). If the price of x increases by $1.00, then the new prices are (P1, P2) = (5.00, 1.00).
To calculate the compensating variation, we can use the following formula:
CV = u(x1, x2) - u(x1', x2')
where u(x1, x2) is Greg's original level of utility, u(x1', x2') is Greg's new level of utility after the price increase, and CV is the compensating variation.
We can find u(x1, x2) using the following steps:
Set x1 = 83 / 4 = 20.75.
Set x2 = 83 - 20.75 = 62.25.
Substitute x1 and x2 into the utility function to get u(x1, x2) = 22.13.
We can find u(x1', x2') using the following steps:
Set x1' = 83 / 5 = 16.60.
Set x2' = 83 - 16.60 = 66.40.
Substitute x1' and x2' into the utility function to get u(x1', x2') = 21.62.
Therefore, the compensating variation is CV = 22.13 - 21.62 = $1.51.
To two decimal places, the compensating variation is $13.52.
Learn more about function here: brainly.com/question/30721594
#SPJ11
Isaiah is mowing lawns for a summer job for every mountain Charlie charges an initial fee of $10 plus $6 dollars for each additional hour
1. write an equation in slope intercept form
2. how much money does he make after working one job for four hours
Answers
Answer:
y = 6x + 10
Isaiah makes $34.00 after working for 4 hours.
Step-by-step explanation:
Slope intercept form is y=mx+b
In this situation the equation would look like so, x = amount of hours:
y = 6x + 10
To solve for how much Isaiah earns after 4 hours plug in 4 instead of x.
y = 6(4) + 10
y = 24 + 10
y = 34
Isaiah makes $34.00 after working for 4 hours.
Hope that helps and have a great day!
I need help, can someone please answer this for me please

Answers
\( \large \tt \: m = - \frac{3}{7} \)
Detailed solution is attached!!~
Answer:
slope = - \(\frac{3}{7}\)
Step-by-step explanation:
Calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (2, \(\frac{2}{7}\) ) and (x₂, y₂ ) = (1, \(\frac{5}{7}\) )
m = \(\frac{\frac{5}{7}-\frac{2}{7} }{1-2}\) = \(\frac{\frac{3}{7} }{-1}\) = - \(\frac{3}{7}\)
For the function f(x) = 2x-4/x+3
What is the x-intercept, y-intercept, and vertical asymptotes
Answers
Answer:
x-intercept: (2,0)
y-intercept: (0,-4/3)
vertical asymptote: x = -3
Step-by-step explanation:
To find the x-intercepts, we can set f(x) to 0, which is y=0:
2x-4/x+3 = 0
2x-4 = 0
2x = 4
x = 2
To find the y-intercepts, we can set x to 0:
2(0)-4/(0)+3 = y
y = -4/3
To find the vertical asymptote, we can set the denominator equal to 0:
x+3 = 0
x = -3
!solve this!
3x + 70 − 7x ≥ 18
Answers
Answer:
3x + 70 − 7x ≥ 18
Step 1: Simplify both sides of the inequality.
−4x + 70 ≥ 18
Step 2: Subtract 70 from both sides.
−4x + 70 − 70 ≥ 18 − 70
−4x ≥ −52
Step 3: Divide both sides by -4.
−4x /−4 ≥ −52 /−4
x ≤ 13
In the united states in 1980 approximately 60 million families had TV's in their home. In 2015 there was almost 100 million families that had TV's in their home. Approximately how many more TV's were there in 2015?
Answers
Answer:
Approximate of 40 Million Televisions
Step-by-step explanation:
there were 40 million more families with televisions in 2015 after a long period of time after 1980
I hope this helped!