Convert 8 centimeters to millimeters.
Answers
Answer:
80mm
Step-by-step explanation:
As 1 cm = 10 mm
8 cm=80 mm
Answer:
80 millimeters
Step-by-step explanation:
Well you convert it
Related Questions
In an examination 1/3 of the total student used unfair means and out of which 1/4 caught red handed while cheating. If 5 student caught red handed then find the total number of student appeared in exam
Answers
Answer:
total number of students =60
Step-by-step explanation:
total number of students 60
used unfair means 1/3= 20
1/4 caught red handed 1/4 of 20= 5
Help I need an answer asap

Answers
Answer:
6
Step-by-step explanation:
To find how many perennials there are, multiply the amount of plants by the percent of perennials. When you multiply percents, just put the percent behind the decimal
60x0.35=21
There are 21 perennials
Do the same for the biennials:
60x0.25=15
Therefore 15 biennials
Subtract the amount of perennials from the amount of biennials
21-15=6
There is 6 more perennials than biennials
Answer:
the answer is 6
21-15=6
Step-by-step explanation.
35% of 60 = 21 for perenalis
25% of 60 = 15 for biennials
40% of 60 = 24 for annuals
A local bank has determined that the daily balances of the checking accounts of its customers are normally distributed with an average of $280 and a standard deviation of $20.a.What percentage of its customers has daily balances of more than $275?b.What percentage of its customers has daily balances of less than $243?c.What percentage of its customers' balances is between $241 and $301.60?
Answers
a. Z-score formula
\(z=\frac{x-\mu}{\sigma}\)where,
• x: observed value
,• μ: mean
,• σ: standard deviation
Substituting with x = $275, μ = $280, and σ = $20, we get:
\(\begin{gathered} z=\frac{275-280}{20} \\ z=-0.25 \end{gathered}\)In terms of the z-score, we need to find
\(P(z\ge-0.25)=1-P(z\le-0.25)\)From the table:
\(P(z\le-0.25)=0.4013\)Then, the percentage of customers that has daily balances of more than $275 is:
\(\begin{gathered} P(z\ge-0.25)=1-0.4013 \\ P(z\ge-0.25)\approx0.6=60\% \end{gathered}\)b. Substituting with x = $243, μ = $280, and σ = $20 into the z-score formula, we get:
\(\begin{gathered} z=\frac{243-280}{20} \\ z=-1.85 \end{gathered}\)In terms of the z-score, we need to find:
\(P(z\le-1.85)\)From the table, the percentage of customers that has daily balances of less than $243 is:
\(P(z\le-1.85)=0.0322=3.22\%\)c. Substituting with x₁ = $241 and x₂ = $301.60, μ = $280, and σ = $20 into the z-score formula, we get:
\(\begin{gathered} z_1=\frac{241-280}{20}=-1.95 \\ z_2=\frac{301.60-280}{20}=1.08 \end{gathered}\)In terms of the z-score, we need to find:
\(\begin{gathered} P(-1.95\le z\le1.08)=P(-1.95\le z\le0)+P(0\le z\le1.08) \\ P(-1.95\le z\le1.08)=0.5-P(z\le-1.95)+P(0\le z\le1.08) \end{gathered}\)From the first table:
\(P(z\le-1.95)=0.0256\)From the second table:
\(P(0\le z\le1.08)=0.3529\)Therefore, the percentage of its customers' balances between $241 and $301.60 is:
\(\begin{gathered} P(-1.95\le z\le1.08)=0.5-0.0256+0.3529 \\ P(-1.95\le z\le1.08)=0.8273=82.73\% \end{gathered}\)

jasper
Answers
of aviation,
there is no way a bee
should be able to fly.
Its wings are too small to get
its fat little body off the ground.
The bee, of course, flies anyway
because bees don't care
what humans think is impossible.
Yellow, black. Yellow, black.
Yellow, black. Yellow, black.
Ooh, black and yellow!
Let's shake it up a little.
Barry! Breakfast is ready!
Ooming!
Hang on a second.
Hello?
- Barry?
- Adam?
- Oan you believe this is happening?
- I can't. I'll pick you up.
Looking sharp.
Use the stairs. Your father
paid good money for those.
Sorry. I'm excited.
Here's the graduate.
We're very proud of you, son.
A perfect report card, all B's.
Very proud.
Ma! I got a thing going here.
- You got lint on your fuzz.
- Ow! That's me!
- Wave to us! We'll be in row 118,000.
- Bye!
Barry, I told you,
stop flying in the house!
- Hey, Adam.
- Hey, Barry.
- Is that fuzz gel?
- A little. Special day, graduation.
Never thought I'd make it.
Three days grade school,
three days high school.
Those were awkward.
Three days college. I'm glad I took
a day and hitchhiked around the hive.
You did come back different.
- Hi, Barry.
- Artie, growing a mustache? Looks good.
- Hear about Frankie?
- Yeah.
- You going to the funeral?
- No, I'm not going.
Everybody knows,
sting someone, you die.
Don't waste it on a squirrel.
Such a hothead.
I guess he could have
just gotten out of the way.
I love this incorporating
an amusement park into our day.
That's why we don't need vacations.
Boy, quite a bit of pomp...
under the circumstances.
- Well, Adam, today we are men.
- We are!
- Bee-men.
- Amen!
Hallelujah!
Students, faculty, distinguished bees,
please welcome Dean Buzzwell.
Welcome, New Hive Oity
graduating class of...
...9:15.
That concludes our ceremonies.
And begins your career
at Honex Industries!
Will we pick ourjob today?
I heard it's just orientation.
Heads up! Here we go.
Keep your hands and antennas
inside the tram at all times.
- Wonder what it'll be like?
- A little scary.
Welcome to Honex,
a division of Honesco
and a part of the Hexagon Group.
This is it!
Wow.
Wow.
We know that you, as a bee,
have worked your whole life
to get to the point where you
can work for your whole life.
Honey begins when our valiant Pollen
Jocks bring the nectar to the hive.
Our top-secret formula
is automatically color-corrected,
scent-adjusted and bubble-contoured
into this soothing sweet syrup
with its distinctive
golden glow you know as...
Honey!
- That girl was hot.
- She's my cousin!
- She is?
- Yes, we're all cousins.
- Right. You're right.
- At Honex, we constantly strive
to improve every aspect
of bee existence.
These bees are stress-testing
a new helmet technology.
- What do you think he makes?
- Not enough.
Here we have our latest advancement,
the Krelman.
- What does that do?
- Oatches that little strand of honey
that hangs after you pour it.
Saves us millions.
Oan anyone work on the Krelman?
Of course. Most bee jobs are
small ones. But bees know
that every small job,
if it's done well, means a lot.
But choose carefully
because you'll stay in the job
you pick for the rest of your life.
The same job the rest of your life?
I didn't know that.
What's the difference?
You'll be happy to know that bees,
as a species, haven't had one day off
in 27 million years.
So you'll just work us to death?
We'll sure try.
Wow! That blew my mind!
"What's the difference?"
How can you say that?
One job forever?
That's an insane choice to have to make.
I'm relieved. Now we only have
to make one decision in life.
But, Adam, how could they
never have told us that?
Why would you question anything?
We're bees.
We're the most perfectly
functioning society on Earth.
You ever think maybe things
work a little too well here?
Like what? Give me one example.
I don't know. But you know
what I'm talking about.
Please clear the gate.
Royal Nectar Force on approach.
Wait a second. Oheck it out.
- Hey, those are Pollen Jocks!
- Wow.
I've never seen them this close.
They know what it's like
For each relation, decide whether or not it is a function.

Answers
Answer:
Relation 1 is a function. Relation 2 is not a function.
Step-by-step explanation:
If the domain is used more than once it is not a function. For example, in Relation 2, -3 was used twice.
The requried, relation 1 is a function, and Relation 2 is not a function, based on the condition of uniqueness in the domain-to-range mapping.
In Relation 1, it is stated that it is a function. This means that each input value (domain) is associated with exactly one output value (range), and there are no repeated domain values.
On the other hand, in Relation 2, it is mentioned that it is not a function. This is because the domain value of -3 is used twice, violating the requirement of a function where each input should have a unique output.
Therefore, Relation 1 is a function, and Relation 2 is not a function, based on the condition of uniqueness in the domain-to-range mapping.
Learn more about function here:
https://brainly.com/question/17009254
#SPJ4
Rewrite the following equation in slope-intercept form.
17x − 10y = 11
Write your answer using integers, proper fractions, and improper fractions in simplest form.
Answers
Answer:
y = 17/10x - 11/10
If you can’t see the photo all the way the answer is y= 17/10x-11/10

Let m = 14 and n = 12 m + 11 + 2n
Answers
Answer:
79
Step-by-step explanation:14+11+2(12) = 24 + 14 + 11 = 79
Answer:
49
Step-by-step explanation:
14+11+2(12)
14+11+24
25+24
49
The area of a square garden is 49 ft^2. How long is each side of the garden?
Answers
Answer:
7
Step-by-step explanation:
Answer:
I think the answer is 7.
Step-by-step explanation:
How many seconds will it take the model rocket to reach its maximum height?

Answers
The answers to the following prompts are give as follows:
9 (c) the time taken for rocket to hit the ground is 5
10 (c) the maximum height is 4
11 (b) the solutions of 16x² - 64 = 0 are -4 and 4
9) To find the time it takes the rocket to hit the ground, we need to find the value of s when h(s) = 0 since h(s) represents the height of the rocket.
So we need to solve the equation: -3s^2 + 6s + 45 = 0.
Factoring, we get -3(s - 5)(s + 3) = 0. So s = 5 or s = -3. Since time cannot be negative, we take s = 5.
Therefore, the answer is (c) 5.
10 ) The maximum height of the rocket occurs at the vertex of the parabola given by the function h(s) = -3s^2 + 6s + 45. The s-coordinate of the vertex is given by s = -b/2a, where a = -3 and b = 6. So s = -6/-6 = 1. Therefore, the answer is (a) 1.
11) We can solve the equation 16x² - 64 = 0 by factoring out the greatest common factor, which is 16: 16(x² - 4) = 0.
Then, we can factor the quadratic expression as a difference of squares: 16(x + 2)(x - 2) = 0. Therefore, the solutions are x = -2 and x = 2, and the answer is (b) -4 and 4.
Learn more about maximum height at:
https://brainly.com/question/11535666
#SPJ1
Please help with this question thanks!!

Answers
Answer:
(-1,4)
Step-by-step explanation:
Step 1) Change both equations to slope intercept form
3x+y=1 ---> y=-3x+1
5x+y=-1 ---> y=-5x-1
Step 2) Plot lines accordingly on graph
Lines intersect at (-1,4)
An aeroplane is 1200 m directly above one end of a field. The angle of depression of the other end of the field from the aeroplane is 64°. How long is the field?
Answers
Answer:
585 m
Step-by-step explanation:
You want to know the length of a field if the angle of depression from a point 1200 m above one end is 64° to the other end.
TangentThe tangent relation is ...
Tan = Opposite/Adjacent
In this problem, the height of the plane is the side opposite the angle of interest, and the adjacent side is the length of the field. Solving for the adjacent side, we get ...
length of field = (height of aeroplane) / tan(64°)
length of field = (1200 m)/2.05030 ≈ 585.28 m
The field is about 585 meters long.

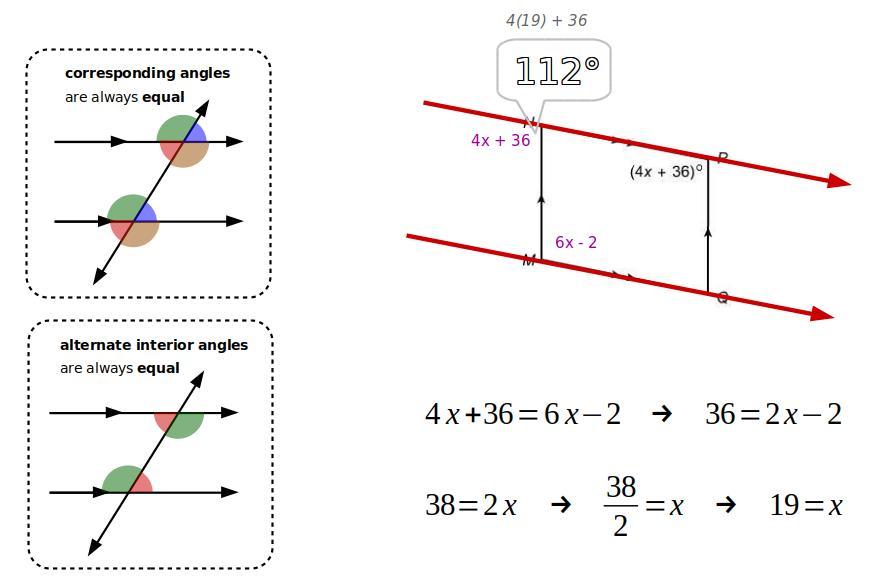
Geometry 6.2
What is m∠N

Answers
Check the picture below.
how do i solve this problem

Answers
The solution to the problem is the simplified expression: 5x³ - x² - 3x + 13.
To solve the given problem, you need to simplify and combine like terms. Start by adding the coefficients of the same degree terms.
(3x³ - x² + 4) + (2x³ - 3x + 9)
Combine the like terms:
(3x³ + 2x³) + (-x²) + (-3x) + (4 + 9)
Simplify further:
5x³ - x² - 3x + 13
In this expression, the highest power of x is ³, and the corresponding coefficient is 5. The term -x² represents the square term, -3x represents the linear term, and 13 is the constant term. The simplified expression does not have any like terms left to combine, so this is the final solution.
Remember to check for any specific instructions or constraints given in the problem, such as factoring or finding the roots, to ensure you address all requirements.
For more such questions on solution
https://brainly.com/question/24644930
#SPJ8
Find the slope of the line graphed below

Answers
Solve the triangle. Round decimal answers to the nearest tenth.

Answers
The value of
1. angle B = 66°
2. a = 14.3
3. b = 24.1
What is sine rule?The sine rule states that if a, b and c are the lengths of the sides of a triangle, and A, B and C are the angles in the triangle; with A opposite a, etc., then a/sinA=b/sinB=c/sinC.
angle B = 180-(81+33)
B = 180 - 114
B = 66°
Using sine rule;
sinB/b = SinC /c
sin66/b = sin81/26
0.914/b = 0.988/26
b( 0.988) = 26 × 0.914
b = 23.764/0.988
b = 24.1
sinC/c = sinA /a
sin81/26 = sin33/a
0.988/26 = 33/a
a = 26×sin33/0.988
a = 14.3
learn more about sine rule from
https://brainly.com/question/20839703
#SPJ1
work done as the particle moves along a straight line from \( (4,0,0) \) to \( (4,3,4) \).
Answers
The work done along the given path is : K (1/4 - 1/√41)
Here, we have,
To find the work done as the particle moves along a straight line from
(4, 0, 0) to (4, 3, 4) under the influence of the force F(r)= Kr/∣r∣³, we need to calculate the line integral of the force over the given path.
The line integral of a vector field F along a curve C is given by:
W=∫_c F⋅dr
where dr is the differential displacement vector along the curve C.
In this case, the curve C is a straight line from (4, 0, 0) to (4, 3, 4).
To compute the line integral, we parameterize the curve C with a parameter t ranging from 0 to 1:
r(t)=(4,0,0)+t((4,3,4)−(4,0,0))
r(t)=(4,0,0)+t(0,3,4)
r(t)=(4,3t,4t)
Now, we can calculate the differential displacement vector dr by taking the derivative of r(t) with respect to t:
dr = dr/dt * dt = (0,3,4)dt
The dot product F⋅dr is given by:
F(r)= Kr/∣r∣³ ⋅(0,3,4)dt
= K(4,3t,4t)/\((4^{2} + (3t)^{2} + (4t)^{2} )^{\frac{3}{2} }\) ⋅(0,3,4)dt
To simplify the dot product, we evaluate r and F at each point:
r=(4,3t,4t)
F = K(4,3t,4t)/\((4^{2} + (3t)^{2} + (4t)^{2} )^{\frac{3}{2} }\)
Taking the dot product, we have:
F.dr = K(4,3t,4t)/\((4^{2} + (3t)^{2} + (4t)^{2} )^{\frac{3}{2} }\) ⋅(0,3,4)dt
= K(25t)/\((25t^{2} + 16 )^{\frac{3}{2} }\) dt
Now, we integrate the dot product over the curve from t=0 to t=1:
W = ∫₀¹ K(25t)/\((25t^{2} + 16 )^{\frac{3}{2} }\) dt
now, integrating we get,
W = K (1/4 - 1/√41)
so, we have,
the work done along the given path is : K (1/4 - 1/√41)
To learn more on integration click:
brainly.com/question/26568631
#SPJ4
complete question:
The force exerted by an electric charge at the origin on a charged particle at a point (x, y, z) with position vector r = (x, y, z) is F(r) = Kr/|r|^3 where K is a constant. find the Work done as the particle moves along a straight line from (4,0,0) to (4,3,4).
Airand Electronics only sells digital tablets and covers.
The Venn diagram shows the number of items sold by Airand Electronics during the first week in May.
Each tablet was sold for £220.
Each cover was sold for £18.
How much money in total did Airand Electronics take in the first week of May?
Answers
The total money that Airand Electronics took on the first week of May is given as follows:
£23,776.
How to obtain the total money?The total money that Airand Electronics took on the first week of May is obtained applying the proportions in the context of the problem.
The amounts are given as follows:
55 tablets -> at 220 pounds.48 tables plus cover -> at 238 pounds.14 covers -> at 18 pounds.Hence the total amount is given as follows:
55 x 220 + 48 x 238 + 14 x 18 = £23,776.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1

Select all fractions that are greater that 1/2
Answers
Answer:
You need to put the fractions for us to answer but fractions that are greater than 1/2 include: 3/4 and 4/7 and basically any fraction that has a value greater than 0.5
Step-by-step explanation:
Given f(x) = x3 - 6x2 + 9x and g(x) = 4 If the domain of f is limited to the closed interval [0,2], what is the range of f? show your reasoning.
Answers
The function f has a range of [0, 2] if the domain of the function is limited to [0, 2]
How to determine the range of the function f?From the question, the definition of the functions are given as
f(x) = x³ - 6x² + 9x
g(x) = 4
The domain of the function f(x) is limited to the interval
Domain = [0, 2]
This means that we calculate the function values at ends of the intervals
i.e. at x = 0 and x = 2
Substitute x = 0 and x = 2 in the equation f(x) = x³ - 6x² + 9x
So, we have
f(0) = 0³ - 6(0)² + 9(0)
f(0) = 0
Also, we have
f(2) = 2³ - 6(2)² + 9(2)
f(2) = 2
So, we have
Range = [f(0), f(2)]
This gives
Range = [0, 2]
Hence, the range of the function f is [0, 2]
Read more about range at
https://brainly.com/question/2264373
#SPJ1
Factorise:
(x - 2y)2 - 12(x - 2y) + 32
Answers
Hi there.
The answer is (x-2y-8)(x-2y-4)
Explanation:
\((x - 2y)^{2} - 12(x - 2y) + 32\)
Let (x-2y) = x
\( {x}^{2} - 12x + 32\)
Then factor the quadratic polynomial by 2 brackets factoring.
\((x - 8)(x - 4)\)
Then convert x to (x-2y)
\((x - 2y - 8)(x - 2y - 4)\)
What is the test that you can do to tell if a graph represents a function?
A
the horizontal line test
B
the vertical line test
C
the expression test
D
the litmus test
Answers
Answer:
djejvjzjwjcxjsjejcjxjsn
Answer:
The answer is B
Step-by-step explanation:
A Vertical Line test.
Find a positive value of a so that the region 0 is less than or equal to y is less than or equal to 5x^a with 0 is less than or equal to x is less than or equal to 1 and constant density has x = 8/13
Answers
a = ln(5) / ln(8/13) is a positive value that satisfies the conditions.
If the region 0 <= y <= \(5x^a\) with 0 <= x <= 1 has a constant density and its x-coordinate is 8/13, then we need to find a positive value of a so that the point\((8/13, 5 * (8/13)^a)\) lies within the region 0 <= y <= \(5x^a.\)
We know that\(0 < = y < = 5x^a, so 0 < = 5 * (8/13)^a < = 5 * (8/13)\). To ensure that the point\((8/13, 5 * (8/13)^a)\)lies within the region, we need to have 0 <= 5 *\((8/13)^a\) <= 5.
Taking the natural logarithm of both sides of\(5 * (8/13)^a\) <= 5 and using the change-of-base formula, we have:
a * ln(8/13) <= ln(5)
Dividing both sides by ln(8/13), we get:
a <= ln(5) / ln(8/13)
Since ln(5) and ln(8/13) are positive, a must also be positive to ensure that the point\((8/13, 5 * (8/13)^a)\) lies within the region.
For more such questions on Logarithm
https://brainly.com/question/25710806
#SPJ4
Which statements are true about the median
Answers
Answer:
First, Third, Fifth statements are true about the median of a data set. Step-by-step explanation: Median is the middle value . Median isn't affected much by one outlier because median is the middle value of an ordered sequences of value
HELPP PLEASE ITS DUE IN A COUPLE OF MINUTES AND IM HAVING TROUBLE

Answers
If the train was traveling nonstop, how many miles would Smith
and Annie have traveled in 5.5 hours?
Answers
Therefore , the solution of the given problem of unitary method comes out to be pace of 50 mph, Smith and Annie would have covered 275 miles in 5.5 hours.
What is an unitary method?The data from this nanosection should be compounded by two in order to complete the task using the unitary method. In essence, the marked by either a set or the pigment parts of the unit method are skipped when a desired object is present. For forty pens, a variable charge of Inr ($1.01) would be required. It's possible that one country will have total influence over the approach taken to accomplish this.
Here,
If the railroad were moving at 50 mph continuously, it would cover 50 miles in an hour.
Thus, the train's route in 5.5 hours would be as follows:
=> 275 miles = 50 mph * 5.5 hours.
Thus, if the train had been moving continuously at a pace of 50 mph, Smith and Annie would have covered 275 miles in 5.5 hours.
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ1
The complete question is "If the train was traveling nonstop at speed of 50 mph, how many miles would Smith
and Annie have traveled in 5.5 hours ?"
What’s the answer for this?? Help (foolish answers will be reported)

Answers
Answer:
the answer is b
Step-by-step explanation:
they should have the same slope so just looking at that you cancel out d. But since it says has a y-intercept of 1 then it would cancel out the other 2. d is perpendicular to it not parallel
Answer:
b. \(y=5x+1\)
Step-by-step explanation:
Slope-intercept form:
\(y=mx+b\)
m is the slopeb is the y-interceptx and y are the corresponding coordinate points (x,y)When two lines are parallel, their slopes are the same. Note the slope of the given equation:
\(y=5x+7\\\\m=5\)
The slope is 5, so the slope for the parallel equation will also be 5:
\(y=5x+b\)
Now insert the given y-intercept:
\(b=1\\\\y=5x+1\)
:Done
Please help me ASAP I need answers

Answers
Answer:
A
Step-by-step explanation:
The product of expression 2x² - 3xy + y² and 2x - 4y will be;
⇒ 4x³ - 14x²y + 14xy² - 4y³
Option c is true.
What is Multiplication?
To multiply means to add a number to itself a particular number of times. Multiplication can be viewed as a process of repeated addition.
Given that;
The equations are,
2x² - 3xy + y² and 2x - 4y
Now,
The product of the expressions are find as;
⇒ (2x² - 3xy + y²) × (2x - 4y)
⇒ 2x²×2x - 2x² × 4y - 3×2×x²×y + 3xy×4y + y²×2x - y²×4y
⇒ 4x³ - 8x²y - 6x²y + 12xy² + 2xy² - 4y³
⇒ 4x³ - 14x²y + 14xy² - 4y³
Thus, The product of expression 2x² - 3xy + y² and 2x - 4y will be;
⇒ 4x³ - 14x²y + 14xy² - 4y³
Learn more about the multiplication visit:
https://brainly.com/question/28768606
#sSPJ2
What is the solution to the equation? ^5√x+7 = -2 (Please help!)
A. -39
B. -17
C. 25
D. no solution

Answers
Step-by-step explanation:
Here we will, Provide index power 5 on both the sides, so that we can cancel out the 5th power root in the L.H.S
so we get as,
==> x+7 = (-2)^5
==> x+7 = -32
==> x = -32-7
==> x = -39
hence, x = -39
Option A.) is correct.
What is the number of sides of a regular polygon whose each exterior angle has a measure of 45 {\ circ 45 ∘?
Answers
The regular polygon has 8 sides and an external angle of 45 degrees on each side.
What is a polygon?A polygon (/pln/) is a closed polygonal chain made up of a finite number of straight line segments that are joined to form a planar figure in geometry (or polygonal circuit).
A polygon is a region that is bounded by a bounding circuit, a bounding plane, or both.
A polygonal circuit's segments are referred to as its edges or sides.
The polygon's vertices (plural: vertices) or corners are the places where two edges converge.
A solid polygon's body is another name for its inside.
A polygon with n sides is referred to as a "n-gon"; a triangle is an example of one.
Simple polygons do not overlap one another.
Mathematicians frequently focus on small polygons' bounding polygonal chains, and they frequently define.
According to our question-
Interior Angles- Angles within a shape, usually a polygon, are referred to as the interior angles of that shape.
∴
Number of sides of a regular polygon
=360/45
8
Hence, The regular polygon has 8 sides and an external angle of 45 degrees on each side.
learn more about polygons click here:
brainly.com/question/26583264
#SPJ4
a folder and a paper clip cost $1.10 in total. the folder costs $1.00 more than the clip. how much does the paper clip cost?
Answers
The paper clip costs $0.05 and the folder Costs $1.00 more, which is $1.05. Together, they add up to the total of $1.10.
Let's solve this problem step by step:
Let's assume the cost of the paper clip is x dollars.
According to the information given, the folder costs $1.00 more than the paper clip, so the cost of the folder would be (x + $1.00).
The total cost of the folder and the paper clip is $1.10, so we can write the equation:
x + (x + $1.00) = $1.10
Combining like terms, we have:
2x + $1.00 = $1.10
Subtracting $1.00 from both sides of the equation, we get:
2x = $0.10
Dividing both sides by 2, we find the value of x:
x = $0.10 / 2
x = $0.05
Therefore, the paper clip costs $0.05.
In summary, the paper clip costs $0.05 and the folder costs $1.00 more, which is $1.05. Together, they add up to the total of $1.10.
For more questions on Costs .
https://brainly.com/question/25109150
#SPJ8