Can the side lengths of 2 9 12 form a triangle yes or no can the side lengths of 3 5 8 form a triangle yes or no can the side lengths of 10 12 15 form a triangle yes or no can the side length of 4 4 7 form a triangle yes or no
Answers
Answer:
2,9 , 12
NO
3,5,8
No
10,12 , 15
Yes
4,4,7
Yes
Step-by-step explanation:
Here, we want to know if the set of given sides will form a triangle
Mathematically, for a triangle to be formed, the sum of two sides must be greater than the third side
If we have a, b and c as sides of a triangle, then mathematically (
a + b > c
a + c > b
and b + c > a
If at any point, these does not work, then we can’t have a triangle
Let us consider the lengths one after the other
We proceed as follows;
2 9 12
Since 2 + 9 is not greater than 12, we cannot have a triangle
3 , 5, 8
Since 3 + 5 equals 8 and not greater than it, we cannot have a triangle
10 , 12 , 15
This forms a triangle
10 + 12 > 15
10 + 15 > 12
12 + 15 > 10
Lastly;
4 , 4 , 7
Since ;
4 + 4 > 7
and
4 + 7 > 4
we have a triangle
Related Questions
HI PLEASE ANSWER THIS QUESTION THANK YOU!
(NO TROLLS PLEASE!)

Answers
There are 30 students in Ms. Prema's history class. 18 of these students turned in an extra credit project at the end of the semester.
Answers
Answer:
12 students didnt turn in a extra credit project at the end of the semester.
Step-by-step explanation:
Which of the following values are in the range of the function graphed below? Check all that apply

Answers
Answer:
B
-10-10=20
10+10=20
20/20=0
25 POINTS AND BRAINLIEST

Answers
Answer:
-2.4
Step-by-step explanation:
-54/22.5= -2.4
If it went down 54 degrees in 22.5 minutes, then you do -54/22.5, which gives you -2.4. So the temperature went down 2.4 F each minute. I think.
After taxes, Alexandra's take home pay is 3 10 of her salary before taxes. Enter and solve an equation to find Alexandra's salary before taxes for the pay period that resulted in $162 of take-home pay. Let s represent your variable. The equation is . Alexandra's salary before taxes for the pay period was $
Answers
Answer:
The equation is 3/10 × s = 162
Alexandra's salary before taxes for the pay period was $540
Step-by-step explanation:
Let
Alexander's salary before taxes
=s
3/10 if Alexander's take home pay is $162 after taxes
3/10 of s = $162
The equation is
3/10 × s = 162
Divide both sides by 3/10
s = 162 ÷ 3/10
= 162 × 10/3
= 1620 / 3
= $540
Alexandra's salary before taxes for the pay period was $540
Remember to multiply or divide both terms by the same value to find equivalent ratios
FIND TWO RATIOS EQUIVALENT TO THE GIVEN RATIO
QUESTION
1. 5/12 2. 14:32
3. 3to4 4. 7/8
Answers
9514 1404 393
Answer:
10/24, 25/607:16, 35:806 to 8, 15 to 2014/16, 35/40Step-by-step explanation:
Just as the directions tell you, multiply both parts of the ratio by the same number. Here, the equivalents we used are 1, 2, and 5 times the numbers in the reduced ratio. Your multipliers can be anything, and don't need to be positive or rational or numbers.
__
1. 5/12 = (5·2)/(12·2) = 10/24
5/12 = (5·5)/(12·5) = 25/60
__
2. 14:32 = (7·2):(16·2) = 7:16
7:16 = (7·5):(16·5) = 35:80
__
3. 3 to 4 = (3·2) to (4·2) = 6 to 8
3 to 4 = (3·5) to (4·5) = 15 to 20
__
4. 7/8 = (7·2)/(8·2) = 14/16
7/8 = (7·5)/(8·5) = 35/40
7/8 = (7·m)/(8·m) = (7m)/(8m) . . . m ≠ 0
A password contains exactly 7 letters. How many passwords are possible if letters cannot be used more than once
Answers
If the password contains exactly 7 letters and letters cannot be used more than once, the number of possible passwords will be the number of ways to choose 7 letters out of the total 26 letters in the alphabet without repetition.
To find out the number of ways to choose 7 letters out of the total 26 letters in the alphabet, we will use the formula for combinations without repetition which is given as, C(n,r) = n! / (r!(n-r)!), where n is the total number of objects, r is the number of objects to be chosen from n and ! is the factorial.
Let's put the values, n = 26 and r = 7C(26,7) = 26! / (7!(26-7)!) = 26! / (7!19!) = (20*21*22*23*24*25*26) / (1*2*3*4*5*6*7)The above expression can be simplified as follows: (20*21*22*23*24*25*26) / (1*2*3*4*5*6*7) = 20*23*25*13 = 149500
Summary: There are 149500 possible passwords of 7 letters from a total of 26 letters if letters cannot be used more than once.
Learn more about combinations click here:
https://brainly.com/question/13604758
#SPJ11
On Friday, Ariel received a $450 paycheck. On
Saturday, she spent $30 on gasoline and $15 on lunch.
What percent of her paycheck did Ariel spend on
Saturday?
Answers
Answer:
10%
Step-by-step explanation:
30+15=45
45 is 10% of 450 as 450/10= 45
william was an early-maturing boy in the 1930s. william would have been predicated to _____.
Answers
Answer:
be a school leader as an adolescent
Step-by-step explanation:
The population of a U.S. City was at 130,000 in 2014. It grew at a rate of 2.6% per year. What is the population today?
Answers
Answer:
155,588
Step-by-step explanation:
The formula for calculating future value:
FV = P (1 + r)^n
FV = Future value
P = Present value
R = growth rate
N = number of years 2021 - 2014 = 7
130,000(1.026)^7 = 155,587.6
rounding off to the nearest whole number is 155,588
To round off to the nearest whole number, look at the first number after the decimal, if it is less than 5, add zero to the units term, If it is equal or greater than 5, add 1 to the units term.
The suns diameter if 10 times the diameter of jupiter. If jupiter is 11 times larger than earth, how much larger than earth is the sun
Answers
Given:
The suns diameter is 10 times the diameter of Jupiter.
Jupiter is 11 times larger than earth.
To find:
How much larger than earth is the sun?
Solution:
Let the diameter of earth be x.
Jupiter is 11 times larger than earth. So,
Diameter of the Jupiter = 11x
The suns diameter is 10 times the diameter of Jupiter. So,
Diameter of sun = 10(11x)
Diameter of sun = 110x
Since, diameter of earth is x and diameter of sun is 110x, therefore, diameter of sun is 110 times of the earth.
Hence, the sun is 110 times larger than earth.
The diameter of the sun is 110 times greater than the diameter of the earth.
What is the linear system?A Linear system is a system in which the degree of the variable in the equation is one. It may contain one, two, or more than two variables.
The sun's diameter is 10 times the diameter of Jupiter. If Jupiter is 11 times larger than earth.
Let the diameter of the Sun, Jupiter, and Earth be S, J, and E respectively
Then we have
S = 10J ...1
J = 11 E ...2
From equations 1 and 2, we have
S = 10 × 11 E
S = 110 E
More about the linear system link is given below.
https://brainly.com/question/20379472
which graph best represents the following inequality y<_ -5/6 +2/3
Answers
The best representation of the inequality y ≤ - 5/6x + 2/3 is shown in figure by red shade region.
What is Inequality?A relation by which we can compare two or more mathematical expression is called an inequality.
We have to given that;
The inequality is,
⇒ y ≤ - 5/6x + 2/3
Now, We can draw the graph of inequality y ≤ - 5/6x + 2/3.
Hence, The best representation of the inequality y ≤ - 5/6x + 2/3 is shown in figure by red shade region.
Learn more about the inequality visit:
https://brainly.com/question/25944814
#SPJ1

(20PTS, Will mark brainliest!) What is the 8th term of the arithmetic sequence with a first term of 7 and a common difference of -3?
Answers
Answer:
the answer is-14 please do you get it
The sixth grade class went to a family fun center. out of the 154 students, 85 played laser tag. A total of 80 students roller skates and 39 of those played laser tag.
Answers
Answer:
Whats the question?
Step-by-step explanation:
What’s the question for the problem?
Given triangle EFG, select the graph of image E 'F'G'and confirm that it preserves length and anglemeasures.(x,y) -(x-3, y + 1)

Answers
We have a transformation for the triangle EFG. In this case is a translation.
We can verify with one of the points which one of the graphs correspond to this transformation.
The transformation is:
(x,y) --> (x-3, y + 1)
We look at point E = (-0.5, 0).
We apply the transformation and get:
(-0.5, 0) --> (-0.5-3, 0+1) = (-3.5, 1)
Then, the graph that has E located in the point (-3.5, 1) is the right one.
An Arithmetic Series Has First Term A And Common Difference D. The Sum Of The First 31 Terms Of The Series Is 310 . (A) Show That A+15d=10. (3) (B) Given Also That The 21st Term Is Twice The 16th Term, Find The Value Of D. (3) (C) The M Th Term Of The Series Is Un. Given That ∑K=1ku∗=0, Find The Value Of K. (4)
Answers
The A + 15d = 10, the value of d is -A when the 21st term is twice the 16th term, and the value of K is either 0 or 1 - 2A/d when ∑k=1ku∗ = 0.
(A) The sum of the first 31 terms of an arithmetic series is given as 310. Using the formula for the sum of an arithmetic series, which is Sn = (n/2)(2a + (n-1)d), we can set up the equation: 310 = (31/2)(2A + 30d). Simplifying this equation leads to 2A + 30d = 20. Rearranging the equation gives A + 15d = 10, which shows that A + 15d is equal to 10.
(B) When the 21st term is twice the 16th term, we can use the formula for the nth term of an arithmetic series, which is An = A + (n-1)d. Setting up the equation 2(A + 15d) = A + 15d + 5d, where the 21st term is 2(A + 15d) and the 16th term is A + 15d, we simplify it to 2A + 30d = A + 20d. By solving this equation, we find that d = -A.
(C) To find the value of K when ∑k=1ku∗ = 0, we need to determine when the sum of the first n terms of the series equals zero. Using the formula for the sum of the first n terms of an arithmetic series, which is Sn = (n/2)(2a + (n-1)d), we set up the equation (K/2)(2A + (K-1)d) = 0. Since the product of two factors is zero, either K/2 = 0 or 2A + (K-1)d = 0. From the first equation, K = 0. From the second equation, we can solve for K in terms of A and d, which gives K = 1 - 2A/d.
Learn more about arithmetic series here:
https://brainly.com/question/30214265
#SPJ11
Is (x + 6) a possible length of a rectangle if the area is x^2 + x − 30? Use an area model to prove your answer.
Can you use an area model to find the length and width of:
Answers
The answer is yes, (x + 6) is a possible length of a rectangle with area x² + x − 30.
To determine whether (x + 6) is a possible length of a rectangle with area x^² + x − 30, we can use an area model to visualize the situation.
First, we need to find the width of the rectangle.
The area of a rectangle is given by the formula A = lw,
where A is the area, l is the length, and w is the width.
We are given that the area is x² + x − 30, so we can set this equal to lw and solve for w:
x² + x − 30 = (x + 6)w
w = (x² + x − 30)/(x + 6)
The length of a rectangle must be greater than or equal to its width, so we need to check whether (x + 6) is greater than or equal to (x² + x − 30)/(x + 6). This simplifies to:
(x + 6) ≥ x² + x − 30
Expanding the left side and simplifying, we get:
x² + 12x + 36 ≥ x² + x − 30
11x ≥ -66
x ≥ -6
Since x must be a positive number (since we are dealing with lengths), we can conclude that (x + 6) is the possible length of the rectangle. Therefore, the answer is yes, (x + 6) is a possible length of a rectangle with an area x² + x − 30.
Learn more about Area here:
https://brainly.com/question/27683633
#SPJ1
calculate area and perimeter

Answers
Answer:
area ≈ 12.505
perimeter ≈ 16.1684
Step-by-step explanation:
We are given
- the radius of the circle (and therefore area of the circle)
- the area of the triangle
We want to find
- angle AOB/AOT. We want to find this because 360/the angle gives us how many OABs fit into the circle. For example, if AOT was 30 degrees, 360/30 = 12 (there are 360 degrees in a circle, so that's where 360 comes from). The area of the circle is equal to πr² = π6² = 36π, and because AOT is 30 degrees, there are 12 equal parts of sector OAB in the circle, so 36π/12=3π would be the area of the sector. A similar conclusion can be reached from the circumference instead of the area to find the distance between A and B along the circle, and OA + AB + BO = the perimeter of the minor sector.
First, we can say that OAT is a right triangle because a tangent line is perpendicular to the line from the center to the point on the circle, so AT is perpendicular to OA. This forms two right angles, one of which is OAT
One thing that we can start to solve is AT. We know that the area of a triangle is equal to base * height /2, and the height of this triangle is AO, with the base being AT. Therefore, we can say
15 = AO * AT / 2
15 = 6 * AT / 2
15 = 3 * AT
divide both sides by 3 to isolate AT
AT = 5
Because OAT is a right triangle, we can say that the hypotenuse ² = the sum of the squares of the two other lengths. The hypotenuse is opposite of the largest angle (in this case, the right angle, as in a right triangle, the right angle is always the largest), so it is OT in this case. The other two sides are OA and AT, so we can say that
OA² + AT² = OT²
5²+6² = OT²
25+36=61=OT²
square root both sides
OT = √61
Next, the Law of Sines states that
sinA/a = sinB/b = sinC/c with angles A, B, and C with sides a, b, and c. Corresponding sides are opposite their corresponding angles, so in this case, AT corresponds to angle AOT, OT corresponds to angle OAT, and AO corresponds to angle ATO.
We want to find angle AOT, as stated earlier, so we have
sin(OAT)/OT = sin(ATO)/OA = sin(AOT)/AT
We know the side lengths as well as OAT/sin(OAT) and want to figure out AOT/sin(AOT), so one equation that helps us get there is
sin(OAT)/OT = sin(AOT)/AT, encompassing our 3 known values and isolating the one unknown. We thus have
sin(90)/√61 = sin(AOT) /5
plug in sin(90) = 1
1/√61 = sin(AOT)/5
multiply both sides by 5 to isolate sin(AOT)
5/√61 = sin(AOT)
we can thus say that
arcsin(5/√61) = AOT ≈39.80557
As stated previously, given ∠AOT, we can find the area and perimeter of the sector. There are 360/39.80557 ≈ 9.04396 equal parts of sector OAB in the circle. The area of the circle is πr² = 36π, so 36π / 9.04396 ≈ 12.505 as the area. The circumference is equal to π * diameter = π * 2 * radius = 12 * π, and there are 9.04396 equal parts of arc AB in the circumference, so the length of arc is 12π / 9.04396 ≈ 4.1684. Add that to OA and OB (both are equal to the radius of 6, as any point from the center to a point on the circle is equal to the radius) to get 6+6 + 4.1684 = 16.1684 as the perimeter of the sector
to 4 percent. If Calvin made monthly payments of $220 at the end of each month, how long would it take to pay off his credit card? a. If Calvin made monthly payments of $165 at the end of each month, how long would it take to pay off his credit card? months (Round up to the nearest unit.)
Answers
Rounding up to the nearest unit, it would take Calvin approximately 27 months to pay off his credit card with a monthly payment of $165.
To determine how long it would take Calvin to pay off his credit card, we need to consider the monthly payment amount and the interest rate. Let's calculate the time it would take for two different monthly payment amounts: $220 and $165.
a. Monthly payment of $220:
Let's assume the initial balance on Calvin's credit card is $3,000, and the annual interest rate is 4 percent. To calculate the monthly interest rate, we divide the annual interest rate by 12 (number of months in a year):
Monthly interest rate = 4% / 12 = 0.3333%
Now, we can calculate the time it would take to pay off the credit card using the monthly payment of $220 and the monthly interest rate. We'll use a formula for the number of months required to pay off a loan with fixed monthly payments:
n = -(log(1 - (r * P) / A) / log(1 + r))
Where:
n = number of months
r = monthly interest rate (as a decimal)
P = initial balance
A = monthly payment
Plugging in the values:
n = -(log(1 - (0.003333 * 3000) / 220) / log(1 + 0.003333))
Using a calculator, we can find:
n ≈ 15.34
Rounding up to the nearest unit, it would take Calvin approximately 16 months to pay off his credit card with a monthly payment of $220.
b. Monthly payment of $165:
We can repeat the same calculation using a monthly payment of $165:
n = -(log(1 - (0.003333 * 3000) / 165) / log(1 + 0.003333))
Using a calculator, we find:
n ≈ 26.39
Please note that these calculations assume that Calvin does not make any additional charges on his credit card during the repayment period. Additionally, the interest rate and the balance are assumed to remain constant. In practice, these factors may vary and could affect the actual time required to pay off the credit card balance.
Learn more about interest rate at: brainly.com/question/28236069
#SPJ11
which graph shows the solution to the system of linear equations?
y=-1/3x+1
y=-2x-3

Answers
y = -1/3x + 1
y = -2x - 3
We can compare the equations to the graphs and see which graph represents the intersection point of the two equations.
The first equation, y = -1/3x + 1, has a negative slope (-1/3) and a y-intercept of 1.
The second equation, y = -2x - 3, also has a negative slope (-2) and a y-intercept of -3.
Based on the slopes and y-intercepts, we can identify the correct graph by finding the point where the two lines intersect.
Unfortunately, since the graphs are not provided, I am unable to determine which specific graph shows the solution to the system of linear equations. I recommend referring to the graph representation of the equations and identifying the intersection point to determine the correct graph.
a local amateur ice skater estimates that the probability she will place first in the next regional competition is 0.56. what are the odds she will win this competition? a) 14 to 39 b) 11 to 14 c) 33 to 17 d) 39 to 14 e) 14 to 11 f) none of the above.
Answers
The odds she will win this competition is 14 to 11.
What is probability?
Probability refers to potential. A random event's occurrence is the subject of this area of mathematics. The range of the value is 0 to 1. Mathematics has incorporated probability to forecast the likelihood of various events. The degree to which something is likely to happen is basically what probability means. The potential outcomes for a random experiment using this fundamental theory of probability, which is also applied to the probability distribution. Knowing the total number of outcomes is necessary before we can calculate the likelihood that a specific event will occur.Odds in favor of an event is ratio of probability of an event to its completion:
Probability =0.56 / 1-0.56
= 0.56/0.44
= 56/44
= 14/11
Hence, the odds she will win this competition is 14 to 11.
To know more about probability check the below link:
https://brainly.com/question/25870256
#SPJ4
find the area of the parallelogram whose vertices are $\bold{0}$, $\bold{a}$, $\bold{b}$, and $\bold{a} \bold{b}$, where $\bold{a}$ and $\bold{b}$ are the vectors defined in part (a).
Answers
The area of the parallelogram formed by the given vertices A(1, 0, -1), B(1, 7, 2), C(2, 4, -1), and D(0, 3, 2) is 2√21 square units.
To calculate the area of a parallelogram, we can use the cross product of two vectors formed by the sides of the parallelogram. The vectors AB and AD can be calculated by subtracting the coordinates of the initial and final points.
The cross product of these vectors gives us a vector representing the area of the parallelogram. Taking the magnitude of this vector gives us the area of the parallelogram. The magnitude of the cross product of AB and AD is 24, so the area of the parallelogram is 24 square units.
In this case, the vector AB is (-3, 7, 3), and the vector AD is (-1, 3, 3). Taking the cross product of these vectors gives us the vector (-12, 6, 24). The magnitude of this vector is √(12² + 6² + 24²) = √756 = 2√21. Therefore, the area of the parallelogram is 2√21 square units.
Complete Question:
Find the area of the parallelogram whose vertices are A(1, 0, −1), B(1, 7, 2), C(2, 4, −1), D(0, 3, 2).
Learn more about parallelogram:
brainly.com/question/28854514
#SPJ11
+16-(-24)+(-8)-16+(12)-(+36)=???
Answers
Answer:
-8
Step-by-step explanation:
+16-16=0
-(-24)+12-(+36)=0
So +16-(-24)+(-8)-16+(12)-(+36)=-8
Answer: -8
Step-by-step explanation:
Given expression
16 - (-24) + (-8) - 16 + (12) - (36)
Expand parentheses and change signs when [-] sign is in front
=16 + 24 - 8 - 16 + 12 - 36
Combine all the terms through addition/subtraction
=40 - 8 - 16 + 12 - 36
=32 - 16 + 12 - 36
=16 + 12 - 36
=28 - 36
=\(\boxed{-8}\)
Hope this helps!! :)
Please let em know if you have any questions
Write the expression in expanded form.
(4.2z)(-5y-3)
Answers
DETAILS PREVIOUS ANSWERS MY NOTES ASK YOUR TEACHER Find the critical numbers of the function. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.)
g(x) = e^8Xcosh(10x)
Answers
To find the critical numbers of the function provided , we need to determine the values of x at which the derivative of g(x) equals zero or does not exist.
First, let's find the derivative of g(x). Applying the product rule and chain rule, we have:
\(g'(x) = 8e^{(8x)cosh(10x) + e^(8x)(10sinh(10x))}\\ = e^{(8x)(8cosh(10x) + 10sinh(10x))\)
Now, to find the critical numbers, we set g'(x) equal to zero and solve for x:
\(e^{(8x)(8cosh(10x) + 10sinh(10x)) = 0\)
8cosh(10x) + 10sinh(10x) = 0
\(8((e^{(10x) + e^(-10x))/2) + 10((e^(10x) - e^(-10x))/2) = 0\)
on simplifying and combining like terms , will get:
\(9e^{(10x) }+ e^{(-10x) = 0\)
Dividing both sides by \(e^{(-10x)\), we obtain:
\(9e^{(20x)\) = -1
Taking the natural logarithm of both sides, we have:
ln(9) + 20x = ln(-1)
However, ln(-1) is undefined since the natural logarithm is only defined for positive values. Therefore, there are no critical numbers for the function g(x) = \(e^{8x)}cosh(10x).\)
learn more about derivative here:
https://brainly.com/question/2921860
#SPJ11
prove that either x or y is divisible by 3 in primitive pythagorean triple
Answers
In a primitive Pythagorean triple, the sides a, b, and c are all integers, and they satisfy the equation a^2 + b^2 = c^2.
Now, let's assume that neither x nor y is divisible by 3. This means that x and y can only be 1, 2, 4, 5, 7, or 8 modulo 3. Therefore, x^2 and y^2 can only be 1 or 4 modulo 3. Now, let's consider the equation a^2 + b^2 = c^2 mod 3. If a and b are both 1 or both 2 modulo 3, then their squares will add up to 2 modulo 3, which is not a quadratic residue. Therefore, one of a and b must be 0 modulo 3, and hence, c must also be divisible by 3. We assumed that neither x nor y is divisible by 3. We then looked at the possible residues of x and y modulo 3 and saw that they can only be 1, 2, 4, 5, 7, or 8 modulo 3. We then used the fact that the sum of two quadratic residues is not a quadratic residue modulo 3, and concluded that one of a and b in the Pythagorean triple must be divisible by 3.
In conclusion, either x or y in a primitive Pythagorean triple must be divisible by 3. This is a result of the fact that the sum of two quadratic residues is not a quadratic residue modulo 3.
to know more about quadratic visit:
brainly.com/question/22364785
#SPJ11
√81r⁶s⁴ simplified and kept in radical form
Answers
Answer:
its A
Step-by-step explanation:
i did the test
(1 point) standard automobile license plates in a country display 2 numbers, followed by 3 letters, followed by 2 numbers. how many different standard plates are possible in this system? (assume repetition of letters and numbers is allowed.) your answer is :
Answers
Therefore ,there are 158,184,000 ways to create a license plate in this system.
What is combination ?A selection from a group of separate items is called a combination in mathematics, and the order in which the elements are chosen is irrelevant (unlike permutations). An apple and a pear, an apple and an orange, or a pear and an orange are three combinations of two fruits that can be chosen from a set of three fruits, such as an apple, an orange, and a pear. Formally speaking, a set S's k-combination is a subset of S's k unique components. Two combinations are therefore equal if and only if they have the same elements in both combinations.
According to the counting principle, the total number of ways to obtain a license plate is calculated by multiplying the number of times each of these events might occur together.
The first number (the digits 1 through 9) can be obtained in nine different ways.
There are 26 methods to obtain the first letter. There are 26 ways to obtain the following letter (repetition is acceptable).
There are 26 methods to get the third letter, 10 ways to get the next number (zero is acceptable), and 10 ways to get the following number with repetitions.
How many ways are there to get the next number? 10 ways\s.
Thus ,total options for obtaining a license plate:
9 x 26 x 26 x 26 x 10 x 10=158184000
Therefore ,there are 158,184,000 ways to create a license plate in this system.
To know more about combination , visit
https://brainly.com/question/27058178
#SPJ4
a hexadecimal number is a number written in the base 16 number system.
t
f
Answers
True. Hexadecimal numbers are written using the base 16 number system, where digits range from 0 to 9 and A to F. They are commonly used in computer systems for concise representation and easy conversion to binary.
In the hexadecimal number system, there are 16 symbols used to represent values, namely 0-9 and A-F. Each digit in a hexadecimal number represents a multiple of a power of 16.
The symbols 0-9 represent the values 0-9, respectively. The symbols A-F represent the values 10-15, respectively, where A represents 10, B represents 11, C represents 12, D represents 13, E represents 14, and F represents 15.
For example, the hexadecimal number "3F" represents the value (3 * 16^1) + (15 * 16^0) = 48 + 15 = 63 in decimal.
Similarly, the hexadecimal number "AB8" represents the value (10 * 16^2) + (11 * 16^1) + (8 * 16^0) = 2560 + 176 + 8 = 2744 in decimal.
Hexadecimal numbers are commonly used in computer systems, as they provide a convenient way to represent large binary numbers concisely. Each hexadecimal digit corresponds to a four-bit binary number, allowing for easy conversion between binary and hexadecimal representations.
for such more question on Hexadecimal numbers
https://brainly.com/question/28280312
#SPJ8
Can you help me with this? 7
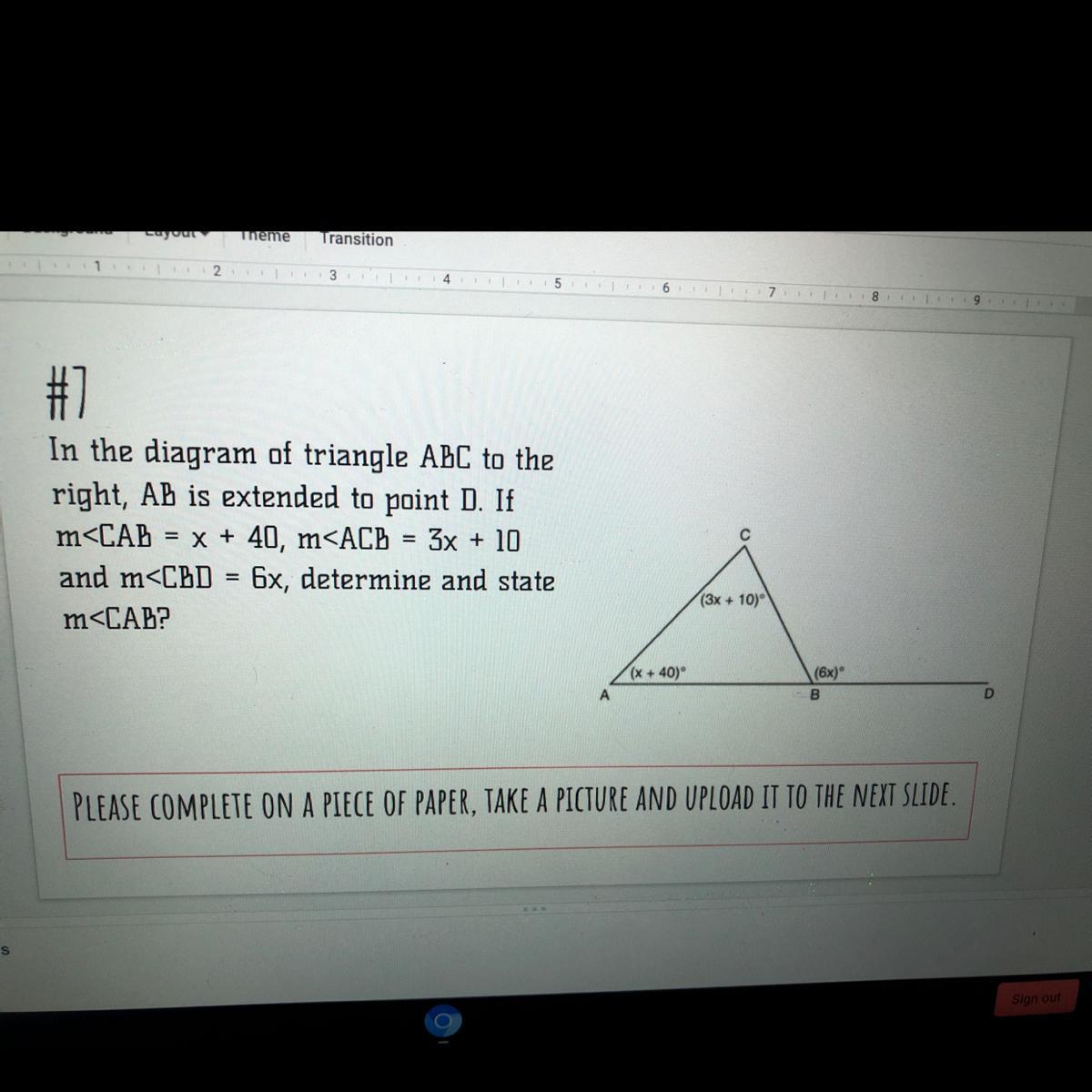
Answers
Answer:
65º
Step-by-step explanation:
The angle of a straight line is 180º, so ∠ABD=180º and ∠ABC=(180-6x)ºThe sum of the interior angles of a triangle is 180, so (x+40)º+(3x+10)º+(180-6x)º=180We can solve from there, x+40+3x+10+180-6x=180Combine like terms, -2x+230=180Subtract 230, -2x=-50Divide by -2, x=25m∠CAB=(x+40)º=(25+40)º=65ºm∠ABC=(180-6x)º=(180-150)º=30ºm∠BCA=(3x+10)º=(75+10)º=85º