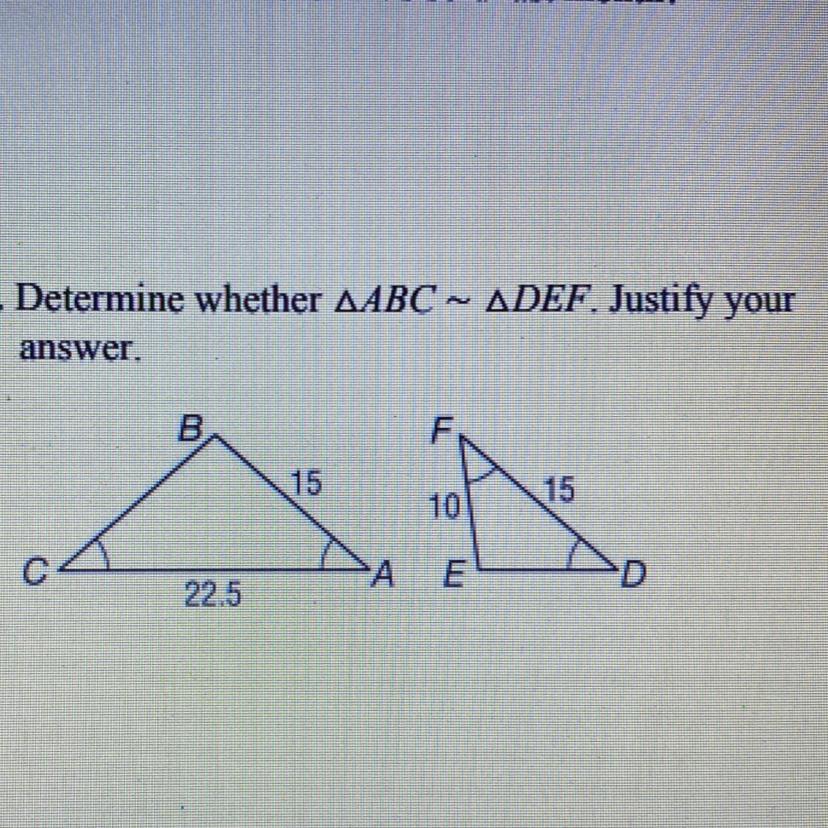
Answers
Answer:
No
Step-by-step explanation:
No, because BA is the same side as EF and the difference is 5. But CA is the same side as ED and the difference is 7.5. All sides would have to increase or decrease by the same number to get to the other triangle and in this case they do not.
answer is no
Related Questions
What are the first five terms in the recursive sequence defined by
a1=2
a2=3
an=an-2*an-1
?
Answers
The first five terms in the recursive sequence are: 2, 3, 6, 18, 108.
First five terms of the recursive sequence defined by a1 = 2, a2 = 3, and an = an-2 * an-1.
1. First term (a1): Given as 2.
2. Second term (a2): Given as 3.
3. Third term (a3): To find a3, use the formula an = an-2 * an-1. In this case, n = 3, so a3 = a1 * a2 = 2 * 3 = 6.
4. Fourth term (a4): Similarly, to find a4, use the formula with n = 4. So a4 = a2 * a3 = 3 * 6 = 18.
5. Fifth term (a5): Finally, to find a5, use the formula with n = 5. So a5 = a3 * a4 = 6 * 18 = 108.
The first five terms in the recursive sequence are: 2, 3, 6, 18, 108.
For more questions on recursive sequence
https://brainly.com/question/30909372
#SPJ11
Given a circle with measures of (C, d, and r) and a circle with measures of (C', d', and r), what is Cits
es )))
= 0.25 and C = 16?
Answers
Answer:
yes
Step-by-step explanation:
Mathematically, C’ = πd’
C’ =16, π = 22/7
∴ 16 = 22d’/7
16 x 7 = 22d’
d' = (16 x 7) / 22
d’ = 112/22
d’ = 5.09
d d’ = 0.25
d’ = 5.09
∴ d (5.09) = 0.25
d = 0.25/5.09
d = 0.05
Mathematically, C = πd
π = 22/7, d = 0.05
∴ C = 22/7 x 0.05
C = 0.16
a card is to be selected at random from 400 cards that are numbered with whole numbers from 1 to 400. how many of these cards have at least one 6 printed on them?
Answers
There are 20 cards with at least one 6 printed on them in a deck of 400 cards numbered from 1 to 400.
Let's find the number of cards with a 6 in the tens place in a deck. There are 10 possible numbers in the ones place (0-9) and only one possible number in the tens place (6), so, 10 x 1 = 10 cards with a 6 in the tens place.
Next, let's find the number of cards with a 6 in the ones place. There are 10 possible numbers in the tens place (0-9) and only one possible number in the ones place (6), so, 10 x 1 = 10 cards with a 6 in the ones place.
Finally, let's find the number of cards with a 6 in both the tens and ones place. There is only one possible number in the tens place (6) and only one possible number in the ones place (6), so, 1 x 1 = 1 card with a 6 in both the tens and ones place.
To find the total number of cards with at least one 6 printed on them is: 10 + 10 + 1 = 21.
However, we need to subtract the number of cards with a 6 in both the tens and ones place, since we counted those cards twice: 21 - 1 = 20.
Know more about questions related to cards here:
https://brainly.com/question/28714039
#SPJ11
Which sequences are geometric? check all that apply.
5, 10, 20, 50, ellipsis
3, 12, 48, 192, ellipsis
3, 15, 75, 375, ellipsis
8, 15, 75, 375, ellipsis
14, 21, 28, 35, ellipsis
17, 20, 23, 26, ellipsis
2, 10, 50, 250, ellipsis
Answers
1.3.19
The selling price of a refrigerator, is $677.50. If the markup is 25% of the dealer's cost, what is the dealer's cost of the refrigerator?
Answers
Answer: $542
Step-by-step explanation:
Given the following :
Selling price of refrigerator = $677.50
Markup = 25% of dealers' cost
Dealers' cost of refrigerator =?
Selling price = Dealers' cost + markup
Markup = 25% of dealers' cost
Let dealers' cost = d
Hence,
Selling price = d + 25% of d
Selling price = d + 0.25d
Selling price of refrigerator = $677.50
Then,
$677.50 = d + 0.25d
$677.50 = 1.25d
d = $677.50 / 1.25
d = $542
Simplify z1= 5 (cos 20 degrees in sin 20 degrees)
Answers
The value of ( 5 ( cos 20° + i sin 20° ) )³ is 125 ( 1/2 + i √3/2 )
let z = ( 5 ( cos 20° + i sin 20° ) )³
We know that DeMoivre's theorem
( cos α + i sin α )ⁿ = ( cos n.α + i sin n.α )
z = ( 5 ( cos 20° + i sin 20° ) )³
z = 5³ ( cos ( 3 × 20 )° + i sin ( 3 × 20 )° )
= 125 ( cos 60° + i sin 60° )
= 125 ( 1/2 + i √3/2 )
Hence, the value of ( 5 ( cos 20° + i sin 20° ) )³ is 125 ( 1/2 + i √3/2 )
Learn more about DeMoivre's theorem here
https://brainly.com/question/28035659
#SPJ4
Given question is incomplete, the complete question is below
How do you use DeMoivre's Theorem to simplify ( 5 ( cos 20° + i sin 20° ))³
Convert the complex number to trigonometric form. z = − 4 +4√3 i

Answers
The complex number -4 + 4√3i can be written in a trigonometric form as \(8(cos(-\pi/3) + isin(-\pi/3)).\) Option D.
How to solveTo convert the complex number to trigonometric form, we need to find its magnitude and argument.
The magnitude (r) can be calculated using the formula r = \(\sqrt(a^2 + b^2),\) where a and b are the real and imaginary parts of the complex number, respectively.
In this case, a = -4 and b = 4√3.
So, r = \(\sqrt((-4)^2 + (4\sqrt3)^2) = \sqrt(16 + 48) = \sqrt64\)
= 8.
The argument (θ) can be found using the formula θ = arctan(b/a). In this case, θ = arctan((4√3)/-4) = arctan(-√3) = -π/3.
Therefore, the complex number -4 + 4√3i can be written in a trigonometric form as \(8(cos(-\pi/3) + isin(-\pi/3)).\) Option D.
Read more about complex numbers here:
https://brainly.com/question/10662770
#SPJ1
At the first school , there were 5 Sixth graders for every 2 seventh graders. At the second school dance, there were 7 sixth graders for 8 seventh graders . Are the ratios of sixth to Seventh on graders at both school dance equivalents. Explain
Answers
Answer:
No
Step-by-step explanation:
The ratio of the first school is 5/2. The ratio of the second school is 7/8.
If the point (-1, 3) is ), and then reflected across the x-axis, what are the coordinates of the final resulting image?
Choose one answer.
a. (-1,3)
b. (-3,-1)
c. (3,-1)
d. (3,1)
Answers
17. Solve v =
(7)(-3).
Answers
Answer:
-21
Step-by-step explanation:
(7)(-3) = 7 x -3 = -21
The Kid Laroi
Angle Q and angle R are complementary angles. If angle R = 73°,
find angle Q.
Answers
Answer:
Angle Q = 17°
Step-by-step explanation:
Complementary means the angles add up to 90°
Using this, do 90° - 73°. This equals 17°, giving you Angle Q.
Answer:
Q = 17
Step-by-step explanation:
Complementary angles add to 90 degrees
Q + R = 90
Q +73 = 90
Q = 90-73
Q = 17
What is the slope of a line passing through the points (2, 5) and (0, -4)?
Answers
Answer:
\(Slope = \dfrac{9}{2}\)
Step-by-step explanation:
The general equation of a line in slope-intercept form is
y = mx + b
where m = slope and b = y-intercept is rise over run
\(m = \dfrac {(y_{2} - y_{1})} {(x_{2} - x_{1})}\)
where (x₁, y₁) and (x₂, y₂) are any two points on the line
For the line passing through (2, 5) and (0, -4) , the slope
\(m = \dfrac{-4 - 5}{0 - 2}\)
\(m = \dfrac{-9}{-2}\)
\(m = \dfrac{9}{2}\)
In decimal that would be m = 4.5
Because slope equals to y2-y1/x2-x1
Draw the cross-sectional effect diagrams for the beam whose loading condition is given in the figure ({N}, {T}, {M})
Answers
A cross-sectional effect diagram, also known as an axial force-shear force-bending moment diagram or simply an internal force diagram, is a graphical representation that shows the distribution of internal forces (axial force, shear force, and bending moment) along the length of a structural member, such as a beam or column.
To draw the cross-sectional effect diagrams for the beam whose loading condition is given in the figure, we need to follow these steps:
Step 1: Identify the type of loadingFor this question, the loading conditions are {N}, {T}, {M}. So, the loading types are axial force, shear force, and bending moment.
Step 2: Draw the cross-sectional diagram of the beam. We need to draw the diagram of the cross-section of the beam in the direction of the forces acting on the beam. In this case, it will be a rectangular beam.
Step 3: Draw the effect diagrams After drawing the cross-sectional diagram, we need to draw the effect diagrams for each loading condition.
The effect diagrams are as follows: 1. Axial force diagram (N):In this case, the axial force is positive (+) which means it is a tensile force. 2. Shear force diagram (T):The shear force is negative (-) from x = 0 to x = 1, which means the shear force is acting downward. It is zero at x = 1 and then becomes positive (+) from x = 1 to x = 2, which means the shear force is acting upward. 3. Bending moment diagram (M):The bending moment is zero at x = 0, becomes negative (-) from x = 0 to x = 1, reaches a minimum at x = 1, and then becomes positive (+) from x = 1 to x = 2.
Learn more about bending movement :https://brainly.com/question/31385809
#SPJ11
the specified probability. round your answer to four decimal places, if necessary. p(0
Answers
The probability that 0 < Z < 2.03 is approximately 0.4788. This means that about 47.88\% of the values in a standard normal distribution are between 0 and 2.03.
To find the probability using a z-score, you need to use a formula that involves subtracting the mean and dividing by the standard deviation of the normal distribution. Then, you can look up the corresponding probability in a z-table, which shows the probability of a value being less than, greater than, or between certain z-scores.¹²
To answer your question, you need to use the formula and the z-table.
The formula for finding a z-score is:
z = \frac{x - \mu}{\sigma}
where x is the value, \mu is the mean, and \sigma is the standard deviation of the normal distribution.
Since you are given that Z follows a standard normal distribution, you can assume that \mu = 0 and \sigma = 1. Therefore, the formula simplifies to:
z = x
To find the probability that 0 < Z < 2.03, you need to find the area under the curve between these two values. You can do this by using the z-table.
First, look up the value 0 in the z-table. You will find that the probability that Z < 0 is 0.5. This means that half of the area under the curve is to the left of 0.
Next, look up the value 2.03 in the z-table. You will find that the probability that Z < 2.03 is 0.9788. This means that most of the area under the curve is to the left of 2.03.
To find the probability that 0 < Z < 2.03, you need to subtract these two probabilities:
P(0 < Z < 2.03) = P(Z < 2.03) - P(Z < 0)
P(0 < Z < 2.03) = 0.9788 - 0.5
P(0 < Z < 2.03) = 0.4788
Therefore, the probability that 0 < Z < 2.03 is approximately 0.4788. This means that about 47.88\% of the values in a standard normal distribution are between 0 and 2.03.
to learn more about probability click here:
brainly.com/question/29221515
#SPJ11
the complete question is:
Find The Specified Probability. Round Your Answer To Four Decimal Places, If Necessary. P(0<Z≪2.03)
A bakery sells mocha cupcakes and vanilla cupcakes. One day it sold 328 mocha and 72 vanilla. What percent of the cupcakes sold that day were mocha?
Answers
x 2x=27 when y=9 and z=2
Answers
number 1 i need help with please

Answers
The volume of the cube is 1.82 in³
How to find the volume of the cube?We know that the formula for the area of the cube, as a function of the volume, is:
A = 326*V^(2/3)
Solving that equation for V, we will get.
V = (A/326)^(3/2)
Then the volume of a cube whose surface area is A = 486 square inches is:
V = (486 in²/326)^(3/2)
V = 1.82 in³
Learn more about volume at:
https://brainly.com/question/1972490
#SPJ1
A rectangular prism kiddie pool is 7 feet wide, 6 feet long, and 10 feet tall. When the day started the pool was completely full of water. After 3 hours, the water level had decreased by 1.5 feet. What would be the volume of water in the kiddie pool after 3 hours. Which dimension would relate to water level?
Answers
Answer:
The volume of water in the kiddie pool after 3 hours will be 357 cubic feet (ft³)
Height is the dimension that would relate to water level.
Step-by-step explanation:
The volume of a rectangular prism can be calculated using the formula
\(V = lwh\)
\(V\) is the volume
\(l\) is the length
\(w\) is the width
and \(h\) is the height
From the question,
When the day started the pool was completely full of water, that is, the volume of water in the pool will be the capacity of the rectangular prism kiddie pool.
From the question,
\(l\) = 6 feet
\(w\) = 7 feet
\(h\) = 10 feet
Hence,
\(V = 6 feet \times 7 feet \times 10 feet\)
\(V = 420 cubic feet (ft^{3} )\)
This is the volume of the water in the pool when the day started.
Also, from the question
After 3 hours, the water level had decreased by 1.5 feet, that is the height had decreased by 1.5 feet
Then, the new height is
10 feet - 1.5 feet = 8.5 feet
h = 8.5 feet
Now, to determine the volume after 3 hours
\(V = 6 feet \times 7 feet \times 8.5 feet\)
\(V = 357 cubic feet (ft^{3} )\)
Hence, the volume of water in the kiddie pool after 3 hours will be 357 cubic feet (ft³)
The dimension that would relate to water level will be the height.
How do you find the third side of an inequality of a triangle?
Answers
To find the third side of an inequality of a triangle, you must first use the Triangle Inequality Theorem.
This theorem states that for any triangle, the sum of any two sides of the triangle must be greater than the third side. This means that in order to find the length of the third side, you must subtract the sum of the two known sides from the smaller of the two sides, then the length of the third side will be equal to the difference between these two numbers. For example, if two sides of a triangle have lengths of 4 and 3, the third side must be greater than 1 (4 + 3 = 7 and 4 - 3 = 1). Therefore, the length of the third side must be greater than 1.
Learn more about Triangle Inequality Theorem here:
https://brainly.com/question/1163433
#SPJ4
Which of the following functions is graphed below?

Answers
3.
Find a relationship between x and y so that (x, y) is equidistant from the two points (3,-1)
and (2,5). Show your work.
Answers
Answer:
The answer is 6.082763
Step-by-step explanation:
We use the Distance formula for this problem.
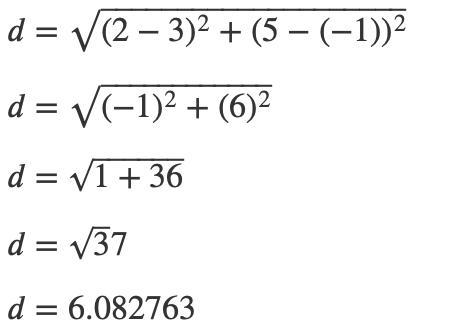
Use long divison to divide the following: (3x^2+5x-2)/(3x-1). Show your work.
Answers
Dividing 3x² + 5x - 2 by 3x - 1 will result to a quotient of x + 2 and a remainder of 0 by application of the long division method
Long division methodThe procedure for long division consists of the following steps:
Divide.Multiply.Subtract.Bring down the next term, and Repeat the process to get zero or arrive at a remainder.We shall divide the 3x² + 5x - 2 by 3x - 1 using the long division method as follows;
Step1:
3x² divided by 3x equals x
3x - 1 multiplied by x equals 3x³ - x
subtract 3x³ - x from 3x² + 5x - 2 will result to 6x - 2.
Step2:
6x divided by 3x equals 2
3x - 1 multiplied by 2 equals 6x - 2
subtract 6x - 2 from 6x - 2 will result to a remainder of 0 (zero).
Therefore, by the long division method, we have quotient of x + 2 and a remainder of 0.
Learn more about long division here: https://brainly.com/question/25289437
#SPJ1
a political action committee launches a new advertisement aimed at building support for a policy that would expand health insurance to low-income americans through increased government funding. according to zaller’s receive-accept-sample (ras) model, who would be most susceptible to this message?
Answers
According to Zaller's Receive-Accept-Sample (RAS) model, individuals who are most susceptible to the message of a political action committee launching a new advertisement aimed at expanding health insurance to low-income Americans through increased government funding would be those who both receive and accept the message.
The RAS model suggests that individuals have varying levels of political knowledge and are exposed to different sources of information. Those who are more likely to receive the message are individuals who are politically interested and engaged, while those who are more likely to accept the message are individuals who have limited political knowledge and are less critical of the information presented to them.
Therefore, in the context of the advertisement aiming to expand health insurance to low-income Americans, the most susceptible individuals would be those who are politically interested but have limited political knowledge. These individuals may be more likely to accept the message without critically evaluating its content.
Learn more about Zaller's model:
https://brainly.com/question/6956833
#SPJ11
A spider ate 25\%25%25, percent more bugs this month than last month. The spider ate 888 bugs last month.
Answers
Answer:
1110
Step-by-step explanation:
888*(1+25%)
=1110
PLS GIVE BRAINLEST
Answer:10
Step-by-step explanation:
the u.s. bureau of labor statistics reports that 11.3% of u.s. workers belonged to unions in 2013. suppose a sample of 400 u.s. workers is collected in 2018 to determine whether union efforts to organize have increased union membership. if the sample results show that 58 of the workers belonged to unions, what is the p-value for your hypothesis test?
Answers
Since the p-value is greater than the commonly used significance level of 0.05, we fail to reject the null hypothesis. Therefore, we do not have sufficient evidence to conclude that union efforts to organize have increased union membership.
We can use a one-sample proportion test to determine if the proportion of union members in the sample is significantly different from the population proportion of 11.3%.
The null hypothesis is that the population proportion is equal to 11.3%:
H0: p = 0.113
The alternative hypothesis is that the population proportion is greater than 11.3%:
Ha: p > 0.113
The sample proportion is P = 58/400
= 0.145
The standard error of the sample proportion is:
SE = √(p*(1-p)/n)
= √(0.113*(1-0.113)/400)
= 0.0197
The test statistic is:
z = (P - p) / SE
= (0.145 - 0.113) / 0.0197
= 1.6244
The p-value for this test is the probability of getting a z-score of 1.6244 or greater, assuming the null hypothesis is true:
p-value = P(Z > 1.6244)
= 0.0515 (using a standard normal distribution table)
To know more about hypothesis test,
https://brainly.com/question/30588452
#SPJ11
Write a polynomial f(x) that satisfies the given conditions.
Polynomial of lowest degree with zeros of -4(multiplicity 1) 1( multiplicity 2)and with F(0)=-12
Answers
If -4 is a zero with multiplicity 1, then (x + 4) is a factor of the polynomial. Similarly, if 1 is a zero with multiplicity 2, then (x - 1)^2 is a factor of the polynomial. Therefore, we can write the polynomial in factored form as:
f(x) = a(x + 4)(x - 1)^2
where "a" is a constant that we need to determine.
To find "a", we use the fact that f(0) = -12. Substituting x = 0 into the equation above, we get:
f(0) = a(0 + 4)(0 - 1)^2
-12 = -4a
Solving for "a", we get:
a = 3
Therefore, the polynomial is:
f(x) = 3(x + 4)(x - 1)^2
Note that this polynomial has a zero at x = -4 (with multiplicity 1), a zero at x = 1 (with multiplicity 2), and f(0) = -12.
−1.8 and 2.6 find the distance on a number line
Answers
Answer:
4.4
Step-by-step explanation:
Please help
How many 1/5 cups are in 2/15 cups of cookie dough?
Answers
Answer:
There are 2/3 of 1/5 cups in 2/15 cups of cookie dough.
Step-by-step explanation:
1/5=3/15
Divide 2/15 by 3/15 using keep, change, flip rules
2/15x15/3=30/45=6/9=2/3
(3x^2-9x+4)+(x^2+2x-10)
Answers
The answer would be 4x^2-7x-6
evaluate the probability that the fuel tank (f) is empty, given also the observation that the battery is flat. which probability is lower? comment on the results.
Answers
Introduction:
Probability is a measure of the likelihood that a given event will occur. In this scenario, the event of interest is the fuel tank being empty, given the observation that the battery is flat. Evaluating the probability of this event involves finding the relationship between the fuel tank and the battery, and using this information to calculate the probability that the fuel tank is empty.
Detailed explanation:
To evaluate the probability of the fuel tank being empty given the observation that the battery is flat, we need to use Bayes' theorem. Bayes' theorem states that the probability of event A given event B can be calculated as follows:
P(A|B) = P(B|A) * P(A) / P(B)
Where P(A|B) is the probability of event A given event B, P(B|A) is the probability of event B given event A, P(A) is the probability of event A, and P(B) is the probability of event B.
In this scenario, event A is the fuel tank being empty, and event B is the battery being flat. To calculate the probability of the fuel tank being empty given the battery is flat, we need to find the values of P(B|A), P(A), and P(B).
Suppose we have the following information:
P(A) = 0.1 (the probability that the fuel tank is empty)
P(B|A) = 0.8 (the probability that the battery is flat given that the fuel tank is empty)
P(B) = 0.05 (the probability that the battery is flat)
Using these values, we can calculate P(A|B) as follows:
P(A|B) = P(B|A) * P(A) / P(B) = 0.8 * 0.1 / 0.05 = 0.16
This means that the probability that the fuel tank is empty given the battery is flat is 0.16.
In conclusion, the probability that the fuel tank is empty given that the battery is flat is lower than the probability that the fuel tank is empty, which was 0.1. This suggests that having a flat battery decreases the likelihood that the fuel tank is empty.
Here you can learn more about evaluate the probability
https://brainly.com/question/29495352#
#SPJ11