Answers
Answer:
ur answer is right lol
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
Related Questions
Given the polar equation r _ 6 cos θ + 4 sin θ - (a) Convert it to an equation in rectangular coordinates, and name the conic section which is its graph. (b) Set up an integral for the arclength of the curve for 0 0 Do not evaluate (c) Set up an equation in θ and find points with vertical tangents.
Answers
(a) Rectangular equation: \((x-3)^2/9 + y^2/4 = 1;\) conic section: ellipse centered at (3, 0) with semi-major axis 3 and semi-minor axis 2.
(b) Integral for arclength: \(s = \int [0,\pi /2] \sqrt{(72 + 112 cos 2\theta )} d\theta\).
(c) Equation for vertical tangents: θ = arctan(3/4) or θ = arctan(-4/3) + π, corresponding to points on the ellipse at (3+3cos(arctan(3/4)), 2sin(arctan(3/4))) and (3+3cos(arctan(-4/3)+π), 2sin(arctan(-4/3)+π)).
(a) To convert the polar equation to rectangular coordinates, we use the following relations:
x = r cos θ
y = r sin θ
Substituting r = 6 cos θ + 4 sin θ into these expressions, we get:
\(x = (6 cos \theta + 4 sin \theta) cos \theta = 6 cos^2 \theta + 4 sin \theta cos \theta\)
\(y = (6 cos \theta + 4 sin \theta ) sin \theta = 6 sin \theta cos \theta + 4 sin^2 \theta\)
Expanding these expressions using trigonometric identities, we get:
x = 3 + 3 cos 2θ
y = 2 sin 2θ
Thus, the rectangular equation of the curve is:
\((x - 3)^2/9 + y^2/4 = 1\)
This is the equation of an ellipse centered at (3, 0) with semi-major axis 3 and semi-minor axis 2.
(b) To set up an integral for the arclength of the curve, we use the formula:
\(ds = \sqrt{(dx/d\theta ^2 + dy/d\theta ^2) d\theta }\)
We have:
dx/dθ = -6 sin θ + 4 cos θ
dy/dθ = 6 cos θ + 8 sin θ
So,
\((dx/d\theta )^2 = 36 sin^2 \theta - 48 sin \theta cos \theta + 16 cos^2 \theta\)
\((dy/d\theta )^2 = 36 cos^2 \theta + 96 sin \theta cos \theta + 64 sin^2 \theta\)
Therefore,
\(dx/d\theta^2 = -6 cos \theta - 4 sin \theta\)
\(dy/d\theta^2 = -6 sin \theta + 8 cos \theta\)
And,
\((dx/d\theta^2)^2 = 36 cos^2 \theta + 48 sin \theta cos \theta + 16 sin^2 \theta\)
\((dy/d\theta ^2)^2 = 36 sin^2 \theta - 48 sin \theta cos \theta + 64 cos^2 \theta\)
Adding these expressions together and taking the square root, we get:
\(ds/d\theta = \sqrt{(72 + 112 cos 2\theta) }\)
To find the arclength of the curve, we integrate this expression with respect to θ from 0 to π/2:
\(s = \int [0,\pi /2] \sqrt{(72 + 112 cos 2\theta )} d\theta\)
(c) To find points on the curve with vertical tangents, we need to find values of θ where dy/dx is infinite.
Using the expressions for x and y in terms of θ, we have:
dy/dx = (dy/dθ)/(dx/dθ) = (6 cos θ + 8 sin θ)/(-6 sin θ + 4 cos θ)
Setting this expression equal to infinity, we get:
-6 sin θ + 4 cos θ = 0
Dividing both sides by 2 and taking the arctangent, we get:
θ = arctan(3/4) or θ = arctan(-4/3) + π
Plugging these values into the expressions for x and y, we get the corresponding points with vertical tangents.
For similar question on vertical tangents.
https://brainly.com/question/15288179
#SPJ11
i need help with dis oki


Answers
Answer:
15 mph
Step-by-step explanation:
You need to find how much each side of the table is changing each time and change that into a fraction. In this example, the change in time is .5 hours. Repeat with the other side to get 12.5 miles. Next you change it into a fraction with the distance over the time to get 12.5/.5. Type this into the calculator to get the answer which is 15 mph.
I dont understand what to do?
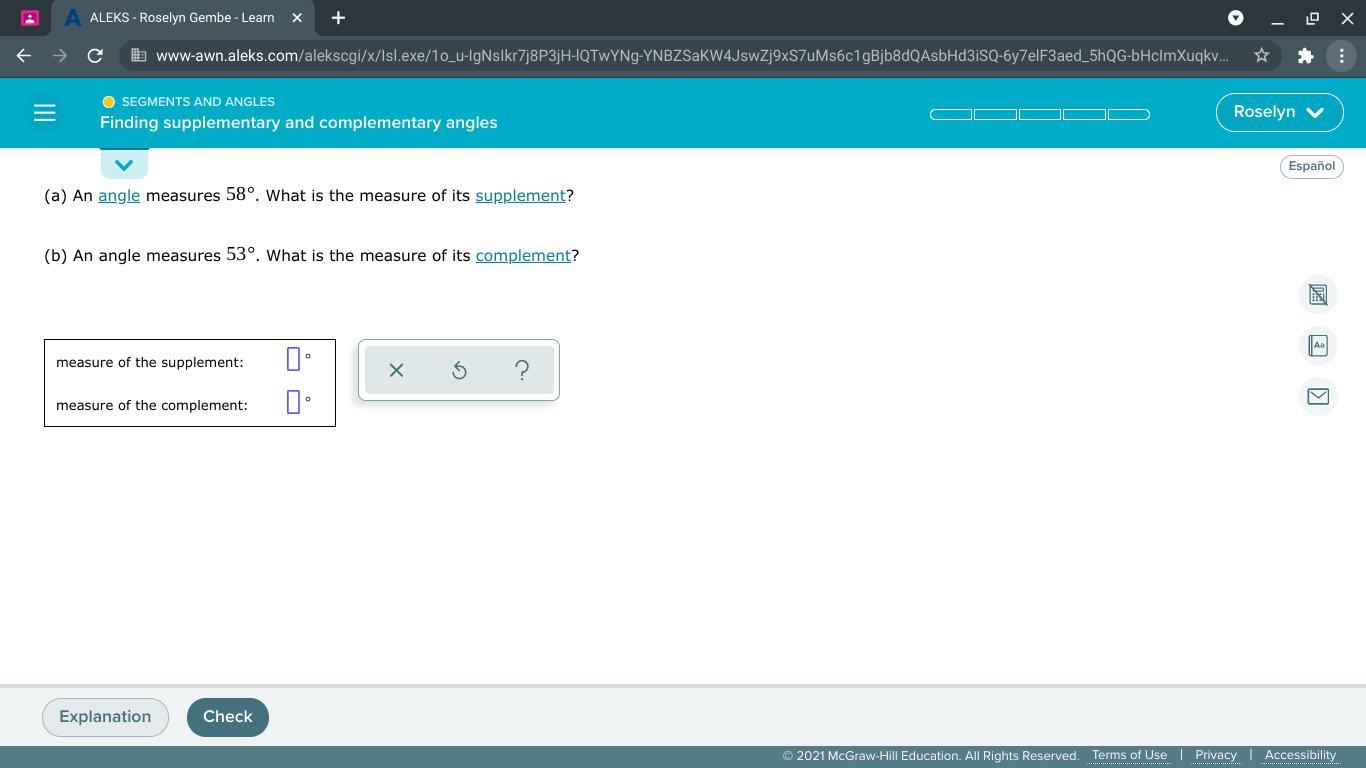
Answers
Answer:
a) 122°
b) 37°
Step-by-step explanation:
a) supplement angle of 58° = 180° - 58° =122°
b) complement angle of 53° = 90° - 53° = 37°
Please figure this out for me will give 30 points to whoever answers first (30 points is all I have)
Answers
The equation of the line passing through points (3,1) and (9,5) found using the equation of the line through two points is:
y = 2x/3 - 1
What is meant by the equation of a line?
A statement that affirms the equivalence of two expressions joined by the equals symbol "=" is known as an equation. Two expressions are combined in an equation using an equal symbol ("="). The "left-hand side" and "right-hand side" of the equation are the two expressions on either side of the equals sign.
The set of points that make up a line in a coordinate system is represented algebraically by a line's equation. An equation of a line is an algebraic expression that represents the many points that together make up a line in the coordinate axis as a set of variables, x, and y.
We are asked to find the equation of a line.
1) (3,1) and (9,5)
(x1, y1) = (3,1)
(x2,y2) = (9,5)
slope of the equation m = y2 -y1 / x2 - x1 = 5-1 / 9-3 = 4/6 = 2/3
The equation of a line through two points is:
y - y1 = m (x-x1)
y - 1 = 2/3 ( x - 3)
y -1 = 2x/3 - 2
y = 2x/3 - 1
2) (x1, y1) = (1,1)
(x2,y2) = (-2,7)
slope of the equation m = y2 -y1 / x2 - x1 = 7-1 / -2-1 = 6/-3 = -2
The equation of a line through two points is:
y - y1 = m (x-x1)
y - 1 = -2 ( x - 1)
y -1 = -2x + 2
y = -2x + 1
3) (x1, y1) = (-4, -3)
(x2,y2) = (8,0)
slope of the equation m = y2 -y1 / x2 - x1 = 0-(-3) / 8-(-4) = 3/12 = 1/4
The equation of a line through two points is:
y - y1 = m (x-x1)
y + 3 = 1/4 ( x +4)
y + 3 = x/4 + 1
y = x/4 -2
Similarly, the equation of the line can be found for other points as well.
Therefore the equation of the line passing through points (3,1) and (9,5) found using the equation of the line through two points is:
y = 2x/3 - 1
To learn more about equations, follow the link.
https://brainly.com/question/18831322
#SPJ1
3/2+1/1
This is my question
Answers
Answer:
2 1/2
Step-by-step explanation:
A bag contains ten tlles labeled B, C, D, E, F, G, H, I, J, and K. One tile will be randomly picked.What is the probability of picking a letter that is not a vowel?Write your answer as a fraction in simplest form.

Answers
The number of vowels is:
\(2\)The total number of tiles is:
\(10\)Therefore, the total number of letters not vowels is given by:
\(10-2=8\)Hence, the probability of picking a letter that is not a vowel:
\(\frac{8}{10}=\frac{4}{5}\)Therefore the required probability is 4/5
meridians of identify degrees east and west of the . these lines are / are not (circle) scientifically based. why/why not?
Answers
The meridians of longitude identify the degrees east and west of the Prime Meridian. These lines are scientifically based because they are determined by the Earth's rotation and provide a consistent and accurate system for navigation, mapping, and timekeeping.
1. The meridians of longitude are imaginary lines that run vertically from the North Pole to the South Pole on the Earth's surface.
2. The Prime Meridian, located at 0 degrees longitude, serves as the starting point for measuring degrees east and west.
3. The degrees of longitude are divided into 360 equal parts, with each degree representing one hour of the Earth's rotation.
4. The meridians of longitude allow us to determine specific locations on the Earth's surface and measure the angular distance from the Prime Meridian.
5. The scientific basis of meridians of longitude enables global coordination and facilitates activities such as international travel, communication, and scientific research.
Learn more about meridians of longitude:
https://brainly.com/question/18779127
#SPJ11
help meeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Answer: 9.7 seconds
Step-by-step explanation:
\(16t^2=1503\\\\t^2 =\frac{1503}{16}\\\\t=\sqrt{1503/16} \text{ } (t > 0)\\\\t \approx 9.7\)
Find the equation of the line that passes through (1,3) and is perpendicular to y=1−2x. Leave your answer in the form y=mx+c
Answers
Answer:
The equation of the line that passes through (1,3) and is perpendicular to y=1−2x is y=1/2x+5/2
Step-by-step explanation:
We can rewrite the original equation as y=-2x+1
To find an equation's perpendicular slope, you take the reciprocal of it and negate it, therefore the perpendicular slope is -2 -> 1/-2 -> 1/2
So far, we have y=1/2x+b, but to find the y-intercept, b, we would need to plug in (1,3) and solve for b:
y=1/2x+b
3=1/2(1)+b
3=1/2+b
5/2=b
Therefore, your final equation is y=1/2x+5/2
If two cards are drawn from a deck, what is the probability that exactly one of the cards will be a face card?
Answers
The probability of getting exactly one face card is 0.72.
According to the questions two cards are drawn from a deck.
Since, we know that
Total number of cards in a deck = 52
Total number of face cards = 3 × 4 = 12
So, the number of ways of selecting 2 cards from a deck = \(^{52} C_{2}\)
And, the total number of ways of getting exactly one face cards
= \(^{12} C_{1} \times ^{40} C_{1}\) + \(^{40} C_{1} \times ^{12} C_{1}\)
= 2\(^{40} C_{1} \times ^{12} C_{1}\)
Therefore, the probability of getting exactly one face card
= \(\frac{2(^{40} C_{1} \times ^{12} C_{1})}{^{52C_{2} } }\)
\(= \frac{2(\frac{40 \times 39!}{1!\times 39!} \frac{12\times 11!}{11!}) }{\frac{52\times 51\times 50!}{2!\times50!} }\)
\(= \frac{2(40\times 12)}{26\times 51}\)
\(=\frac{2\times 480}{1326}\)
= 0.72
Hence, the probability of getting exactly one face card is 0.72.
Find out more information about probability here:
https://brainly.com/question/13293035
#SPJ4
Gabrielle's age is three times Mikhail's age. The sum of their ages is 20 . What is Mikhail's age?
Answers
Answer:
I think Mikhail's age is 5
The question say Gabrielle's age is 3 times his
so 5 × 3 = 15
15 + 5 = 20
I need help with this equation. Please solve for k

Answers
Hey there!
18 = -k + 3
-k + 3 = 18
-1k + 3 = 18
SUBTRACT 3 to BOTH SIDES
-1k + 3 - 3 = 18 - 3
SIMPLIFY IT!
-1k = 18 - 3
-1k = 15
DIVIDE -1 to BOTH SIDES
-1k/-1 = 15/-1
SIMPLIFY IT!
k = 15/-1
k = -15
Therefore, the answer is: k = -15
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
(2 points) conditional probability. a fair coin is tossed twice. (a) (1 point) what is the probability of two heads if we know that the first toss is a head? (b) (1 point) what is the probability of two heads if we know that at least one toss is a head?
Answers
If we know that the first toss is a head, the probability of two heads is 1/2. The probability of two heads if we know that at least one toss is a head is 2/3.
(a) If we know that the first toss is a head, the probability of two heads is 1/2 because the second toss is still independent and has a 50% chance of being either heads or tails.
(b) If we know that at least one toss is a head, the probability of two heads can be found by adding up the probability of getting two heads on the first and second tosses and then getting heads on the first and tails on the second toss. This can be represented as:
P(two heads | at least one head) = P(two heads) / P(at least one head) = (P(heads on first and heads on second) + P(heads on first and tails on second)) / (1 - P(tails on first and tails on second))
Since each toss has a 50% chance of being heads, the probability of getting two heads on the first and second tosses is 0.5 × 0.5 = 0.25. The probability of getting heads on the first and tails on the second is also 0.5 × 0.5 = 0.25. And the probability of getting tails on both tosses is 0.5 × 0.5 = 0.25.
Therefore, the answer is:
P(two heads | at least one head) = (0.25 + 0.25) / (1 - 0.25) = 0.5 / 0.75 = 2/3
So the probability of two heads, if we know that at least one toss is a head, is 2/3.
To know more about probability, here
https://brainly.com/question/30034780
#SPJ4
Some of 100 towns of a kingdom are connected by roads. It is known that for each two towns $A$ and $B$ connected by a road, there is a town $C$ which is not connected by a road with at least one of the towns $A$ and $B.$ Determine the maximum possible number of roads in the kingdom.
Answers
According to the given statement The maximum possible number of roads in the kingdom is 4950.
To determine the maximum possible number of roads in the kingdom, we can use a simple counting argument.
Let's assume that the number of towns in the kingdom is denoted by N. We want to find the maximum number of roads connecting these towns.
According to the problem statement, for any two towns A and B connected by a road, there is a town C that is not connected by a road with at least one of the towns A and B..
This implies that for any pair of towns A and B connected by a road, there is at least one town that is not connected to either A or B. Let's call this town C.
Now, for every pair of towns A and B, there is a town C that is not connected to either A or B. Since there are N towns in total, there are N-2 towns that are not connected to either A or B.
Therefore, for each road connecting A and B, we can choose any of the N-2 towns as the town C that is not connected to either A or B.
Since each road connects two towns, the maximum number of roads in the kingdom is equal to the number of pairs of towns, which can be calculated using the formula for combinations:
N choose 2 = N(N-1)/2
Therefore, the maximum possible number of roads in the kingdom is N(N-1)/2.
In this case, since there are 100 towns in the kingdom, the maximum possible number of roads is (100)(100-1)/2 = 4950.
So, the maximum possible number of roads in the kingdom is 4950.
To know more about number visit:
https://brainly.com/question/3589540
#SPJ11
To determine the maximum number of roads in the kingdom, we assume that each town is connected to all other towns except itself. This ensures that for any pair of towns, there is a town that is not connected to at least one of them. With 100 towns, each connected to 99 others, the total number of roads is 9900.
To determine the maximum possible number of roads in the kingdom, let's consider the given conditions. For any two towns, A and B, connected by a road, there must be a town, C, that is not connected to at least one of the towns, A or B.
To maximize the number of roads, we can start by assuming that each town is connected to all other towns except itself. This would mean that for every pair of towns, A and B, there is a town, C, that is not connected to at least one of them.
Now, let's count the number of roads. If there are 100 towns, each town is connected to 99 other towns (excluding itself). Since there are 100 towns, the total number of roads would be 100 * 99 = 9900 roads.
Therefore, the maximum possible number of roads in the kingdom is 9900.
Learn more about number of roads in the kingdom
https://brainly.com/question/31970815
#SPJ11
Double integrals can only be calculated on rectangular domains. o True o False
Answers
The statement "Double integrals can only be calculated on rectangular domains" is false. Double integrals can be calculated on various types of domains, not limited to rectangular ones. The concept of double integration extends to more general regions, including non-rectangular domains, such as circles, triangles, and irregular shapes.
Double integrals are used to calculate the signed volume or area under a surface or over a region in two-dimensional space. While rectangular domains are often used for simplicity and ease of computation, they are not the only type of domain on which double integrals can be applied. In fact, double integrals can be evaluated on a wide range of regions as long as they satisfy certain conditions. These conditions include being bounded, connected, and having a well-defined boundary. The region can be defined by any shape, including circles, triangles, ellipses, polygons, or irregular curves. To calculate a double integral over a non-rectangular domain, appropriate coordinate transformations or changes of variables may be required. These transformations help to map the non-rectangular domain onto a rectangular one, allowing for the application of standard integration techniques. In conclusion, while rectangular domains are commonly used in double integrals, they are not the only option. Double integrals can be computed on a variety of domains, enabling the evaluation of integrals over non-rectangular regions.
Learn more about Double integrals here:
https://brainly.com/question/27360126
#SPJ11
A dog trainer compared mean numbers of lessons for two
groups of dogs to learn a new trick.
Answer ASAP will give brainliest
Answers
A true statement on the mean number of lessons for the dogs is The mean number of lessons for group A is greater than the mean for group B by 1 MAD.
How to prove the mean number ?The difference in the mean number of lessons between the two groups being Group A and Group B is :
= Mean number of lessons Group A - Mean number of lessons Group B
= 5 - 3
= 2
The mean absolute deviation for Group B is 2. The mean number of lessons of group A related to this is :
= 2 / 2
= 1
This shows that the mean number of lessons for group A is greater than the mean for group B by 1 MAD.
Find out more on Mean Absolute Deviation at https://brainly.com/question/17381861
#SPJ1
The full question is:
Mean number of lessons Mean Absolute Deviation (MAD)
Group A 5
Group B 3
2
2
Which statement about the data is true?
A. The mean number of lessons for group A is greater than the mean for group B by 1 MAD
B. The mean number of lessons for group A is greater than the mean for group B by 2 MAD
C. The MAD for group A is more than the MAD for group B
D. On average, the dogs in group B required more lessons than the dogs in group A
Find the length of PQ.
10
9
P(-10.8)
8
00N
6
5
3
Q(-3, 3)
2
- 10 -98 -7 -6 -5 4 -3 -2 -1

Answers
I think its B about 8.6 units
Find the volume of the triangular pyramid shown below

Answers
Answer:
B
Step-by-step explanation:
consider the infinite geometric series: what is a1? what is r? find the following partial sums: s2
Answers
An infinite geometric series is one in which each term is equal to the preceding term multiplied by a fixed non-zero number, known as the common ratio.
The first term is called a1, and the common ratio is represented by r.In this particular question, we are required to find the value of a1 and r for an infinite geometric series. The partial sum S2 will also need to be found.For a geometric sequence that is infinite, the formula for the partial sum, Sn, is:Sn = a1 / (1-r), where a1 is the first term and r is the common ratio.To solve for a1, it is necessary to know two other variables: the common ratio r and the value of the first term a1. S2 is the sum of the first two terms, so: S2 = a1 + arTo find S2, we must first determine a1 and r. a1 is the first term in the sequence, and r is the common ratio. We can obtain both a1 and r by dividing the second term by the first term.The formula is:r = (ar/a1) = a2/a1 Substitute the value of r and a1 into the formula for S2 to obtain the result: S2 = a1 + ar = a1 + a1r = a1(1+r) Therefore, the value of a1 is a constant number that will appear in the series, and the common ratio, r, will be multiplied by this number to obtain the next value in the series.
So, a1 is the first term, and r is the common ratio of the infinite geometric series. S2, the sum of the first two terms, is found by using the formula S2 = a1 + ar where a1 is the first term and r is the common ratio.
To know more about Geometric series visit-
https://brainly.com/question/30264021
#SPJ11
9.41 x 4.8 with the work pls .
Answers
Answer: 45.168
Step-by-step explanation: First find 941 x 48 = 45168 then put the decimal point at the thrid digit as the decimal in 9.41 is in the 2nd digit and 1st in 4.8 so 2 + 1 = 3 so the answer is 45.168
What a deal! Just deShirts is having a 20% off sale. Trixie rushes to the store and buys 14 shirts. When the clerk rings up her purchases, Trixie sees that the clerk has added the 5% sales tax first, before taking the discount. Trixie wonders whether adding the sales tax before the discount makes her final cost more than adding the sales tax after the discount. Without making any calculations, make a conjecture. Is Trixie getting charged more when the clerk adds sales tax first? The next few problems will help you figure it out for sure.
Does it matter if sales tax is added before the discount or after her final total? (Yes or no AND why or why not?)
Answers
Answer:
no because she would get the same total if she added it before or after
Step-by-step explanation:
Latavia purchased adult and child tickets for the fall festival. Tickets cost $14.88 for each adult and $8.88 for each child. Let x represent the number of adult tickets purchased and y represent the number of child tickets purchased. Write an expression to represent the total cost of the tickets Latavia purchased. (5 points)
a
($14.88 + $8.88)(x + y)
b
($14.88 - $8.88)(x + y)
c
$14.88y + $8.88x
d
$14.88x + $8.88y
Answers
At which root does the graph of f x x 5 3 x 2 2 touch the x axis?
Answers
The root of the graph of f(x) = \((x-5)^{3} (x+2)^{2}\) touches the x axis at -2 and 5.
What is root of graph ?
A rooted graph is a graph in which one node is labeled in a special way so as to distinguish it from other nodes. The special node is called the root of the graph. The rooted graphs on nodes are isomorphic with the symmetric relations on nodes.
Have given,
f(x) = \((x-5)^{3} (x+2)^{2}\)
If a curve touches the x-axis then f(x) = 0
⇒\((x-5)^{3} (x+2)^{2}\) = 0.
But if ab = 0 ⇒ either a = 0 or b = 0 or both zero.
⇒\((x - 5)^{3}\) = 0 and \((x + 2)^{2}\) = 0
⇒ (x - 5) = 0 and x + 2 = 0
⇒ x = 5 and x = - 2.
The root of the graph of f(x) = \((x-5)^{3} (x+2)^{2}\) touches the x axis at -2 and 5.
To learn more about root of graph visit : brainly.com/question/29553394
#SPJ4
PLEASE HELP ASAP DUE LIKE NOW

Answers
Answer:
6
Step-by-step explanation:
Answer:
Hopefully you don't mind that I took a photo instead hope this helps

Find the measures of angle a and B. Round to the nearest degree.

Answers
The measure of angle A and angle B are 28.61 and 61.39 rounded to two decimal place, using trigonometric ratio of tangent for the respective angles.
What is trigonometric ratios?The trigonometric ratios is concerned with the relationship of an angle of a right-angled triangle to ratios of two side lengths.
The basic trigonometric ratios includes;
sine, cosine and tangent.
tan B = 6/11 {opposite/adjacent}
B= tan⁻¹(6/11) {cross multiplication}
B = 28.6105.
tan A = 11/6 {opposite/adjacent}
A= tan⁻¹(11/6) {cross multiplication}
A = 61.3895.
Therefore, the measure of angles A and B are 28.61 and 61.39 rounded to two decimal place, using trigonometric ratio of tangent for the respective angles.
Read more about trigonometric ratios here: https://brainly.com/question/11967894
#SPJ1
Solve for the coordinates of the midpoint of (13, 27) and (-31, 53). Show your work to receive full credit.
Answers
Answer:
-9,40
Step-by-step explanation:
Midpoint Formula:
\((\frac{x^{1} +x^{2} }{2},\frac{y^{1} +y^{2} }{{2} } } )\)
Answer:
Midpoint = (−9,40)
Step-by-step explanation:

Twenty students bought tickets for a school party. All of the money received for these 20 tickets was used to purchase beverages. Then, an additional 10 students bought tickets. Rather than use this additional money to buy more refreshments, all 30 students received a $3.00 refund. How many dollars were used to buy beverages?
Answers
Answer:
$87
Step-by-step explanation:
please answer i will give u brainless PLZZZZZZ

Answers
Answer:
96 green pens
Step-by-step explanation:
Super simple. You do: 14x+15x+24x=212 which is 53x = 212 and x=4
Green = 4*24=96
How does collecting like terms in an expression differ from collecting like terms in
an equation/inequality? Explain.
Answers
Answer:
I think its different from each other because maybe combining like terms in a inequality your trying to compare them? Or maybe they're just advanced. Can someone give me an example of an inequality please so I can try finding out the difference?
the probability of at least one head in two flips of a coin is
Answers
The probability of getting at least one head in two flips of a coin is 3/4 or 0.75, which means that there is a 75% chance of getting at least one head in two flips of a coin.
To find the probability of at least one head in two flips of a coin, we can use the complement rule. The complement of the event "at least one head" is "no heads."
The probability of getting no heads in two flips of a coin is (1/2) x (1/2) = 1/4.
Therefore, the probability of getting at least one head in two flips of a coin is:
1 - (probability of no heads) = 1 - 1/4 = 3/4
The probability of getting at least one head in two flips of a coin is 3/4 or 0.75, which means that there is a 75% chance of getting at least one head in two flips of a coin.
In other words, if you flip a coin twice, the probability of getting at least one head is relatively high, and you are more likely to get at least one head than to get no heads at all.
Find more about probability
brainly.com/question/17144515
#SPJ4
