Brainlist for correct answer and 25 points for answering! Write the equation of a line that is perpendicular to y=0.25x-7 and that passes through the point (-6,8).

Answers
Because the standard slope equation is y=mx+b and in perpendicular lines the slope is opposite of the slope on a parallel line. 0.25 is equal to 1/4 and the opposite of 1/4 is 4/1 but you also make it negative so it’s -4. So we have y=-4x+b and you plug in the coordinates and solve [8=-4(-6)+b and -4*-6=24 so you rewrite it as 8=24+b and 8-24=-16 and -16=b] so you plug in b and the equation is y=-4x-16
Hope this helped
Related Questions
PLEAZE SOMEONE HELP WHAT THE VOLUME OF THIS 7cm AND 6cm

Answers
r=6cm and h=7cm
Volume of right circular cone =31πr2h
=31×722×(6)2×7
=31×22×36
=264cm3
dunno whether the formula is correct or not!
Work out the size of angle x.

Answers
Answer:
x = 46°
Step-by-step explanation:
Angles on a straight line sum to 180°.
Therefore, the interior angle of the triangle that forms a linear pair with the exterior angle marked 130° is:
⇒ 180° - 130° = 50°
The interior angle of the triangle that forms a linear pair with the exterior angle marked 96° is:
⇒ 180° - 96° = 84°
The interior angles of a triangle sum to 180°. Therefore:
⇒ 50° + 84° + x = 180°
⇒ 134° + x = 180°
⇒ 134° + x - 134° = 180° - 134°
⇒ x = 46°
Therefore, the size of angle x is 46°.

what is the distance between (-6,13) and (8,13)
Answers
Explanation:
The distance between two points (x1, y1) and (x2, y2) is:
\(d=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}\)In this problem points are (-6, 13) and (8, 13). The distance is:
\(d=\sqrt[]{(8-(-6))^2+(13-13)^2}=\sqrt[]{(8+6)^2}=8+6=14\)Answer:
The distance is 14
ASAP
Please show working out I will give out brainiest :)

Answers
gusts bc f d b v sbbdjdbhdbdhdhbdndhd
slope = 4, point (3,-2) is on the line
Answers
Answer:
y = 4x + b
Step-by-step explanation:
We know that (3, -2) is on this line. So 3 = m(-2)+b.
This leaves us with two variables the slope (m) and the y intercept (b).
But wait a minute, the slope is given to us since it says slope = 4.
Our equation is now, 3 = 4(-2)+b
3 = -8 + b
b = 11.
Our final equation is now y = 4x + b.
(y,x) is a point on this line.
Hope this helped!
JoeLouis2
what is -6^2 equal to?
Answers
Answer:
-36
Step-by-step explanation:
If they asked (-6)^2 then it would be 36
Answer:
-36
Step-by-step explanation:
Normally, 6²=36 but because it is -6, multiply 6 by itself and add the negative sign.
Carlos had at most 7 hours to spend in an amusement park in which he uses 1 hour for lunch and the rest of the time on park rides. What is the maximum number of rides Carlos can comete if each ride takes 15 minutes?
Answers
Answer:
24
Step-by-step explanation:
7 hours = 420 mins (7×60)
420-60=360 (time taken for lunch)
15mins=one ride
360÷15=24 rides
Representing a Graph with a Slope-Intercept Equation
-5-4-3-2
5
4
3
2
+
2345
y
2 3 4
X
5
A function f(x) is graphed.
What is the slope of the function?
m
What is the y-intercept of the function?
b = v
Which equation represents the graph of the function?

Answers
Answer:
1.) The slope is 2
2.) The y-intercept is (0,1)
3.) y = 2x + 1
Step-by-step explanation:
1.) you can either use rise over run or the slope formula. rise over run is quicker, but here's the formula:
you can use any two points on the line, i chose (2, 5) and (1, 3)
\(\frac{(y_{2}-y_{1})}{(x_{2}-x_{1})} \\\)
\(\frac{3-5}{1-2} \\\\\frac{-2}{-1} \\\\\frac{2}{1} \\\\2\)
2.) for the y-intercept, you just look for the point where the graph crosses the y-axis and x = 0
3.) using the formula y = mx + b, m being the slope and b being the y-intercept, you take the information above and plug it in to get y = 2x + 1
i hope this helped!
What is the approximate value of x? Round to the nearest tenth.

Answers
Answer:
40 degreses
Step-by-step explanation:
there is a right angle and that means it is 90 degreese then it gives you 50 degreese so you add them up and get 140 then you subtract that 140 from 180 and get 40 degreese.
Answer:
c
Step-by-step explanation:
cause it is
Evaluate the expression for p = -1.
7p =
Answers
Answer:
-7
Step-by-step explanation:
Expression: 7p
Value of p: p = -1
Substitute p in the expression with the value given for p, -1.
Then, multiply by 7.
7p = 7 × (-1) = -7
Given: AQ ≅ RQ
∠YAF and ∠FRY are right angles.
Prove: AQY ≅ RQF
Answers
Given: AQ ≅ RQ, it should be noted that AQY ≅ RQF based on SAS Congruence. Therefore, AQY ≅ RQF.
How to explain the informationGiven: AQ ≅ RQ
∠YAF and ∠FRY are right angles.
Prove: AQY ≅ RQF
1. AQ ≅ RQ (Given)
2. ∠YAF and ∠FRY are right angles (Given)
3. ∠AQY = ∠RQF (Vertical angles are congruent)
4. AQ = RQ (Given)
5. AY = RY (Side-Angle-Side Congruence)
6. ∠QYA = ∠RFQ (Angle-Side-Angle Congruence)
7. AQY ≅ RQF (SAS Congruence)
Therefore, AQY ≅ RQF.
Learn more about angle on
https://brainly.com/question/25716982
#SPJ1
Given: AQ ≅ RQ
∠YAF and ∠FRY are right angles.
Prove: AQY ≅ RQF

PLEASE HELP
Video Game Weather
In a video game, the chance of rain each day is always 30%. At the beginning of each day in the
video game, the computer generates a random integer between 1 and 50. Explain how you could
use this number to simulate the weather in the video game.
I
Answers
Answer:
35
Step-by-step explanation:
Raj went to the theatre to watch a traditional Indian dance performance with his family. The theatre had 1050 seats. There were 50% fewer $50-seats than $30-seats. 90% of the $30-seats and some $50-seats were sold. A total of $34 650 was collected. How many seats were unsold?
Answers
Total number of seats that remain unsold are 168.
What is statistics?
The branch of mathematics dealing with data collection, organization, analysis, interpretation and presentation.
Let's start by defining some variables to represent the unknowns in the problem:
Let x be the number of $30-seats.Let y be the number of $50-seats.From the problem, we know that:
The total number of seats is 1050: x + y = 1050.There were 50% fewer $50-seats than $30-seats: y = 0.5x.90% of the $30-seats and some $50-seats were sold, which means that the revenue from the $30-seats is 0.9(30x) = 27x, and the revenue from the $50-seats is 0.9(50y) = 45y.We also know that the total revenue collected is $34,650:
27x + 45y = 34650
Now we can substitute y = 0.5x from the second equation into the third equation and simplify:
27x + 45(0.5x) = 34650
27x + 22.5x = 34650
49.5x = 34650
x = 700
So there were 700 $30-seats and 350 $50-seats.
The number of sold $30-seats is 0.9(30x) = 567, and the number of sold $50-seats is 0.9(50y) = 315.
Therefore, the total number of seats sold is 882, and the number of unsold seats is:
1050 - 882 = 168
Learn more about statistics on:
https://brainly.com/question/15525560
#SPJ1
NEED HELP FAST
Todd bought x gallons of gasoline for $2.75 a gallon. Write an expression that shows how much Todd spent on gas.
Answers
Answer:
2.75x = how much he spent on gas.
You can ask for clarification in the comments if you need more help from me.
Step-by-step explanation:
Pablo grew a plant for school and recorded the growth of the plant
each week. He wrote ordered pairs to organize his data: (1, 5), (2, 8),
(3, 8), (4, 11), (5, 15).
Is this relation a function? Explain.
Answers
Answer:
Yes. the relation is a function
Step-by-step explanation:
Here, we want to check if the relation is a function
if a relation is a function, then every x-values (input values) will have one y-value
No two output values (y values) will have a single x value
Looking at the pairs;
It is a function
Although two x values have same y value; 2 and 3 to 8; no two y values have same x value
Hence, the ordered pairs is a function
Under certain conditions in certain devices, the behavior of the current in a conductor can be represented as a function of time by the equation I(t)=I
0e −t/τ
. Here I 0 is the current at t=0 and τ is known as the time constant. In this case, τ=7.00 ms and the initial current I 0=4.10 mA. Determine the amount of charge passing through a fixed point in the conductor in the time interval t 1=0 to t 2=τ
Answers
Therefore, the amount of charge passing through the fixed point in the conductor in the time interval t1 = 0 to t2 = τ is approximately -18.86 μC.
To determine the amount of charge passing through a fixed point in the conductor in the time interval t1 = 0 to t2 = τ, we need to calculate the integral of the current function I(t) over that time interval.
The current function is given by:
I(t) = I0 * e\(^(-t/τ)\)
Integrating this function over the time interval [t1, t2], we have:
Q = ∫[t1, t2] I(t) dt
Substituting the expression for I(t), we get:
Q = ∫\([t1, t2] I0 * e^(-t/τ) dt\)
Since I0 and τ are constant values, we can take them out of the integral:
Q = I0 * ∫[\(t1, t2] e^(-t/τ) dt\)
To evaluate this integral, we can use the following property of the exponential function:
∫\(e^(ax) dx = (1/a) * e^(ax) + C\)
Applying this property to our integral, we have:
Q = I0 * (-τ) * \(e^(-t/τ) |_t1 ^t2\)
Substituting the values t1 = 0 and t2 = τ, we get:
Q\(= I0 * (-τ) * (e^(-t2/τ) - e^(-t1/τ))\)
Substituting the given values I0 = 4.10 mA and τ = 7.00 ms, we have:
\(Q = 4.10 mA * (-7.00 ms) * (e^(-7.00 ms/7.00 ms) - e^(0/7.00 ms))\)
Simplifying the expression:
\(Q = 4.10 mA * (-7.00 ms) * (e^(-1) - 1)\)
Calculating the value:
Q ≈ -18.86 μC
To know more about interval,
https://brainly.com/question/17070177
#SPJ11
Carl's age is three more than two times Lindsay's age. Carl is 39 years old. How old is Lindsay?
Answers
Answer:
The answer is (39/2)-3=L.
Step-by-step explanation:
Find the length of the arc of the circular helix with vector equation r(t) = 3 cos(t) i 3 sin(t) j tk from the point (3, 0, 0) to the point (3, 0, 2).
Answers
Answer:
Step-by-step explanation:
To find the length of the arc of the circular helix from the point (3, 0, 0) to the point (3, 0, 2), we need to integrate the magnitude of the derivative of the vector equation with respect to the parameter t over the desired interval.
The vector equation of the circular helix is given by r(t) = 3cos(t)i + 3sin(t)j + tk.
To find the derivative of r(t), we differentiate each component with respect to t:
r'(t) = (-3sin(t))i + (3cos(t))j + k
The magnitude of the derivative is given by ||r'(t)|| = sqrt((-3sin(t))^2 + (3cos(t))^2 + 1^2) = sqrt(9sin^2(t) + 9cos^2(t) + 1) = sqrt(9(sin^2(t) + cos^2(t)) + 1) = sqrt(9 + 1) = sqrt(10).
Integrating this magnitude from t = 0 to t = 2 (the desired interval), we have:
Length of the arc = ∫[0 to 2] ||r'(t)|| dt = ∫[0 to 2] sqrt(10) dt = sqrt(10) ∫[0 to 2] dt = sqrt(10) [t] [0 to 2] = sqrt(10)(2 - 0) = 2sqrt(10).
Therefore, the length of the arc of the circular helix from the point (3, 0, 0) to the point (3, 0, 2) is 2sqrt(10) units.
Learn more about circular helix
brainly.com/question/33470920
#SPJ11
a manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 411.0 gram setting. it is believed that the machine is underfilling the bags. a 35 bag sample had a mean of 406.0 grams. a level of significance of 0.05 will be used. state the hypotheses. assume the standard deviation is known to be 25.0.
Answers
Using a 35-bag sample with a mean of 406.0 grams, a known standard deviation of 25.0 grams, and a level of significance of 0.05, you can perform a one-tailed Z-test to determine whether to reject or fail to reject the null hypothesis.
To test if the potato chip manufacturer's bag filling machine is working correctly at the 411.0-gram setting, we will state the hypotheses using the given terms.
Null Hypothesis (H0): The machine fills bags correctly, with a mean weight of 411.0 grams (µ = 411.0 grams)
Alternative Hypothesis (H1): The machine is underfilling bags, with a mean weight less than 411.0 grams (µ < 411.0 grams)
To learn more about standard deviation, refer here:
https://brainly.com/question/23907081#
#SPJ11
Please I keep getting stuck on this I need help so bad!
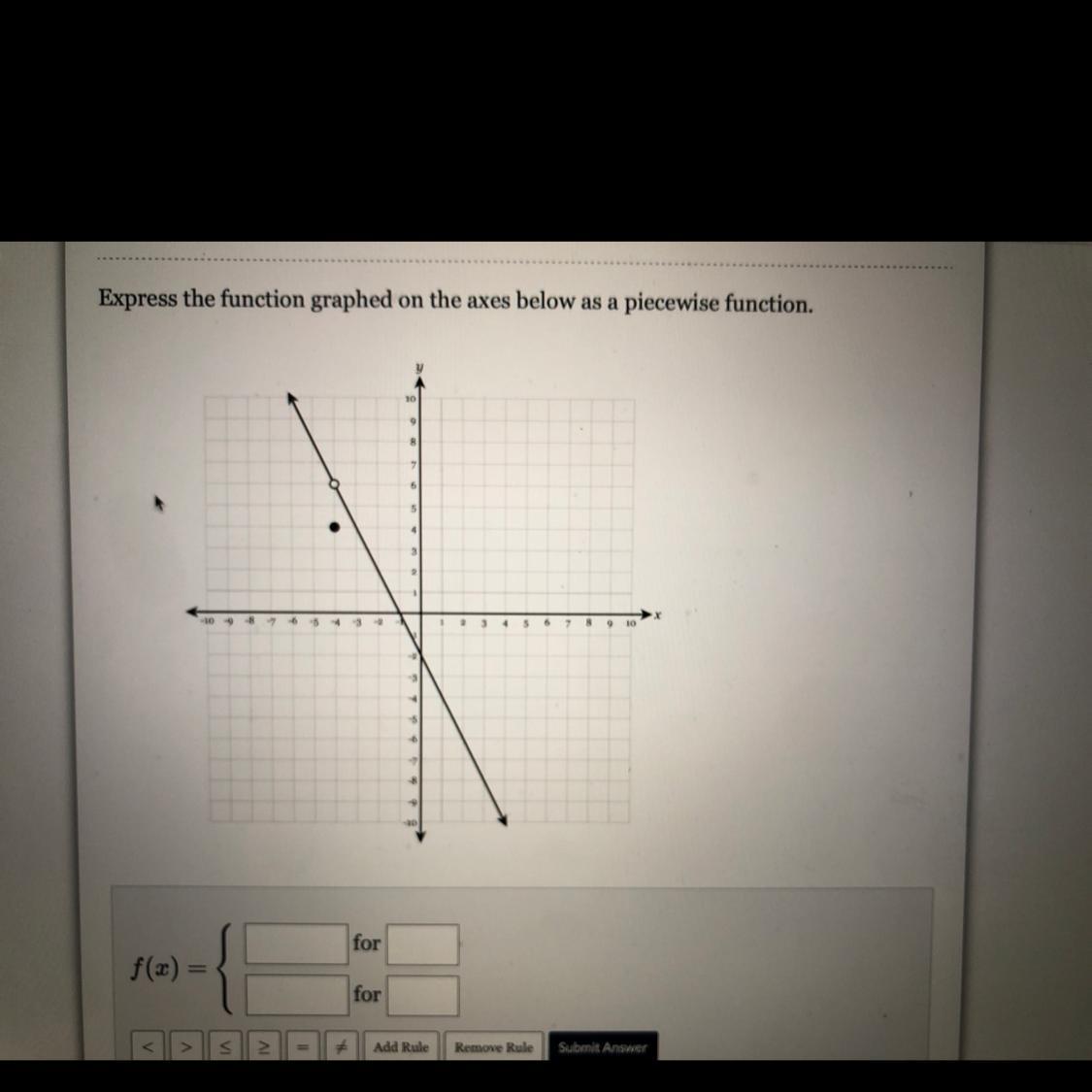
Answers
Answer:
f(x) = -2x -2 ; -∞ < x < -4 and -4 < x < ∞
6 ; x = -4
Step-by-step explanation:
Piecewise function:(-1,0) and (0 ,-2)
Find the slope using the points.
\(\sf slope =\dfrac{y_2-y_1}{x_2-x_1}\)
\(\sf = \dfrac{-2-0}{0-(-1)}\\\\=\dfrac{-2}{0+1}\\\\=-2\)
m = -2
Equation of line in slope y-intercept form: y =mx + b
y = -2x + b
Plugin any of the point in the above equation. (0, -2)
-2 = 0 + b
b = -2
Equation: y = -2x - 2
Hollow circle is the break point.
Function:
f(x) = -2x -2 ; -∞ < x < -4 and -4 < x < ∞
6 ; x = -4
The function graphed on the axes below as a piecewise function is \($f(x)=\left\{\begin{array}{l}-x-1, \text { for }-6 \leq x < 2 \\ -\frac{1}{2} x-4, \text { for } 2 < x < 6\end{array}\right.$\)
The upper piece of the graph is defined on the interval \($-6 \leq x < 2$\). It has a slope of -1 and a y-intercept of -1, so its equation is \($y=-x-1$\).
The lower piece of the graph is defined on the interval \($2 < x < 6$\). It has a slope of -1 / 2 and would cross the y-axis at -4 if it were extended. Its equation is
\(y=-1 / 2 x-4\)
The two pieces together give the function.
\(f(x)=\left\{\begin{aligned}-x-1, & \text { for }-6 \leq x < 2 \\-\frac{1}{2} x-4, \text { for } 2 < x < 6\end{aligned}\right.$$\)
The core concept of mathematics' calculus is functions. The unique varieties of relations are the functions. In mathematics, a function is represented as a rule that produces a distinct result for each input x. In mathematics, a function is indicated by a mapping or transformation. Typically, these functions are identified by letters like f, g, and h. The collection of all the values that the function may input while it is defined is known as the domain. The entire set of values that the function's output can produce is referred to as the range. The set of values that could be a function's outputs is known as the co-domain.
To learn more function visit:
brainly. com/question/12431044
#SPJ1
when dividing 751.6 by 100, how should the decimal point be moved?
Answers
Answer:
Two places to the left = 7.516
Step-by-step explanation:
Answer:
The decimal point should be moved two times to the rightStep-by-step explanation:
751.6 ÷ 100 = 7.516
and that means that
the decimal point moves
two times to the right.
Hope this helps! <3
I dont understand this please help

Answers
Answer: 190 miles
Solution:
=4 x 95 / 2
=(cross out the common factor)
=2 x 95 = 190
If donuts are 12 cents a dozen how much does 100 donuts cost.
Answers
The cost of 100 donuts is $ 1 if a dozen of donuts cost 12 cents.
This question is solved using the unitary method. The unitary method is a method in which you find the value of a unit and then the value of the required number of units.
1 dozen refers to a group of 12.
Cost of 1 dozen donuts or 12 donuts = 12 cents
Cost of 1 donut = \(\frac{12}{12}\) = 1 cent
Cost of 100 donuts = 1 * 100 = 100 cents
100 cents = 1 dollar.
Thus, the cost of 100 donuts is 100 cents or 1 dollar.
Learn more about Unitary Method:
https://brainly.com/question/24587372
#SPJ4
A (4,2) and B (6,0) answer m=
Answers
Answer: 4 − 1 = 3
Step-by-step explanation: 6 - 2 = 4 32 + 42 = 25 4 − 1 = 3
Mason bought 16 tickets to a baseball game. The group rate saved him $5. 75 per ticket. He paid a total of $296. 00 for the tick.
Answers
The regular price of a ticket to the game is: $24.25
What are algebraic operations?They are the set of numbers and symbols that are related by the different mathematical operation signs such as addition, subtraction, multiplication, division among others.
According to the data problem,
Total paid = $296Number of tickets = 16saved per ticket = $5.75Calculating the cost per tickets we get:
Cost per tickets = 296/16 = $18.5
Calculating the regular price we have:
regular price = $18.5 + $5.75 = $24.25
Learn more about algebraic operations at: brainly.com/question/3927786
#SPJ4
Correctly written question:
Mason bought 16 tickets to a baseball game. The group rate saved him $5.75 per ticket He paid a total of $296.00 for the tickets. What was the regular price of a ticket to the game?
Find all values of x for which rank(A)=2. A=⎣⎡2421430x−472316⎦⎤ Find the value of k for which the matrix A=⎣⎡−6−7−879−3−5−5k⎦⎤ has rank 2 . k=
Answers
The value of k for which the matrix A has rank 2 is any real number except -1/6.
Here, we have,
To find the values of x for which rank(A) = 2, we need to determine the row echelon form or reduced row echelon form of matrix A and observe the rows with leading non-zero entries.
Let's perform row operations on matrix A:
A = ⎣⎡2 4 2
1 4 3
0 x − 4 7
2 3 1 6⎦⎤
Performing row operations:
R₂ = R₂ - (1/2)R₁
R₃ = R₃ - (R₁/2)
R₄ = R₄ - (R₁/2)
A = ⎣⎡2 4 2
0 2 1
0 x - 4 -1
0 -1 -2⎦⎤
Now, let's analyze the rows with leading non-zero entries.
The first two rows have leading non-zero entries, so they contribute to the rank of matrix A.
The last two rows are all zeros, so they do not contribute to the rank.
From this analysis, we can see that for rank(A) = 2, the value of x can be any real number.
Moving on to the second part of the question, we need to find the value of k for which the matrix A has rank 2:
A = ⎣⎡-6 -7 -8
7 9 -3
-5 -5k⎦⎤
Performing row operations:
R₂ = R₂ + R₁
R₃ = R₃ - (5/6)R₁
A = ⎣⎡-6 -7 -8
1 2 -11
0 -5k + 2 17/6⎦⎤
To have rank(A) = 2, we need to ensure that the last row is not a multiple of the second row.
So we set the determinant of the 2x2 submatrix formed by the last two rows to be non-zero:
(2)(17/6) - (-5k + 2)(2) ≠ 0
Simplifying the equation:
17/3 + 10k - 4 ≠ 0
10k ≠ -17/3 + 4
10k ≠ -5/3
k ≠ -1/6
Therefore, the value of k for which the matrix A has rank 2 is any real number except -1/6.
To learn more on matrix click:
brainly.com/question/28180105
#SPJ4
.Consider the following function, 12 (v+x²) f(z,y)= if0 < z ≤ y ≤1 5 otherwise. Find the volume, V, contained between z = 0 and == = f(z,y). Hint: Finding the volume under a surface is similar to finding the area under a curve. Think about where foxy) is zero. What can you say about the volume beneath the surface at those locations? a. First, write this as an integral. Do not give your answer in terms of f(x,y). V= 7 dz dy b. Now evaluate the integral to find the volume, V ]]]
Answers
The correct option is b) V = 256(6 + 2√5)/5.
Given, 12 (v + x²) f(z, y) = 0 if 0 < z ≤ y ≤ 1, 5 otherwise. We need to find the volume, V, contained between z = 0 and = f(z, y).
We know that, Volume under a surface = Double integral of the function over the region bounded by the surface in the xy plane.
For finding the volume, we integrate the given function f(z, y) over the given region.
Let us draw the graph of the surface: graph{y<=x^2+4 [-6.16, 6.12, -3.07, 6.11]}
At the point where f(x, y) = 0 is the curve y = x² + 4, i.e., a parabola opening upwards.
Hence, the volume beneath the surface at those locations will be zero. The region enclosed by this surface and xy-plane is shown below.
Thus, the required volume, V is given by, V = ∫∫R f(z, y) dz dy
Here, R is the region enclosed by the surface and the xy-plane.
Hence, we have V = ∫∫R f(z, y) dz dy
Now, we will find the limits of integration.
Since the surface touches the xy-plane at z = 0, the lower limit of z is 0.
Also, since the region R lies between the parabolic cylinder y = x² + 4 and the yz-plane, the limits of integration for y are y = 0 and y = x² + 4. And, the limits of integration for x are x = -2 and x = 2.
Now, we will evaluate the given integral to find V:V = ∫∫R f(z, y) dz dy= ∫02 ∫0x²+4 12(v+x²) dz dy + ∫∫R 5 dz dy= 6(x²+4)(x²+5)dy+5×Area of the region enclosed by the surface in the xy-plane= 6 ∫-2²+4 to 2²+4 (y+5) √y dy + 5(4²) = [6/5(y+5)³/2]∣∣-2²+4 2²+4 + 80= 256(6 + 2√5)/5
So, the correct option is b) V = 256(6 + 2√5)/5.
Visit here to learn more about Volume brainly.com/question/28058531
#SPJ11
If profits decrease by 13.8% when the degree of operating
leverage (DOL) is 3.8, then the decrease in sales is:
A) 0.28%
B) 0.52%
C) 3.63%
D) 10%
E) 52.44%
Answers
Given that profits decrease by 13.8% when the degree of operating leverage (DOL) is 3.8.
The decrease in sales is: We have to determine the percentage decrease in sales Let the percentage decrease in sales be x.
Degree of Operating Leverage (DOL) = % change in Profit / % change in Sales3.8
= -13.8% / x Thus, we have: x
= -13.8% / 3.8
= -3.63%Therefore, the decrease in sales is 3.63%.Hence, the correct option is C) 3.63%. Percentage decrease in sales = % change in profit / degree of operating leverage
= 13.8 / 3.8
= 3.63% The percentage decrease in sales is 3.63%.
To know more about profits, visit:
https://brainly.com/question/29987711
#SPJ11
PLZ HELP ME !!!!!!!!!!!!!!
2 questions

Answers
Answer: D
Step-by-step explanation: I think
Refer to Table S6.1 - Factors for Computing Control Chart Limits (3 sigma) for this problem. A quality inspector took the following samples of the length of time (in seconds) for glue to dry. Please round your calculations to three decimal places. Sample 1 Obs. 1 125 Obs. 3 122 Obs. 2 126 100 155 Obs. 4 132 121 118 Obs. 5 114 125 142 2 130 110 140 129 3 a) What is the value of ? x = seconds (round your response to three decimal places). b) What is the value of R? R= seconds (round your response to three decimal places). c) What are the UCL, and LCL, using 3-sigma? Upper Control Limit (UCL;) = seconds (round your response to three decimal places). Lower Control Limit (LCL;) = seconds (round your response to three decimal places). d) What are the UCLR and LCLR using 3-sigma? Upper Control Limit (UCLR) = seconds (round your response to three decimal places). Lower Control Limit (LCLR) = seconds (round your response to three decimal places).
Answers
To find the value of x, we calculate the average of the sample observations. Summing up the observations and dividing by the total number of observations, we get:
x = (125 + 122 + 126 + 100 + 155 + 132 + 121 + 118 + 114 + 125 + 142 + 2 + 130 + 110 + 140 + 129 + 3) / 17 = 114.118 seconds (rounded to three decimal places).b) To find the value of R, we calculate the range of each sample by subtracting the minimum observation from the maximum observation. Then we find the average range across all samples:R = (155 - 100 + 142 - 2 + 140 - 110 + 132 - 114 + 142 - 3) / 5 = 109.2 seconds (rounded to three decimal places).
c) The Upper Control Limit (UCL) and Lower Control Limit (LCL) using 3-sigma can be calculated by adding and subtracting three times the standard deviation from the average:UCL = x + (3 * R / d2) = 114.118 + (3 * 109.2 / 1.693) = 348.351 seconds (rounded to three decimal places).LCL = x - (3 * R / d2) = 114.118 - (3 * 109.2 / 1.693) = -120.115 seconds (rounded to three decimal places).
d) The Upper Control Limit Range (UCLR) and Lower Control Limit Range (LCLR) using 3-sigma can be calculated by multiplying the average range by the appropriate factor:UCLR = R * D4 = 109.2 * 2.115 = 231.108 seconds (rounded to three decimal places).LCLR = R * D3 = 109.2 * 0 = 0 seconds.
To learn more about observations click here : brainly.com/question/9679245
#SPJ11