Cows and Chickens
A chicken farmer also has cows for
a total of 30 animals, and the
animals have 66 legs in all.
How many chickens does the farmer have?

Answer:

Yes, you are right. Great job!

Step-by-step explanation:

Answer:

Option D: g = 7 and h = 3

Step-by-step explanation:

The polynomial is;

8x² – 8x + 2 – 5 + x

Simplifying this gives;

8x² - 7x - 3

If this is simplified to 8x² – gx – h

Thus, by comparison of terms;

– gx = - 7x

-x will cancel out to get;

g = 7

Similarly, - h = - 3

Thus,h = 3

Therefore; g = 7 and h = 3

Answer:

Option D: g = 7 and h = 3

Step-by-step explanation:

The polynomial is;

8x² – 8x + 2 – 5 + x

Simplifying this gives;

8x² - 7x - 3

If this is simplified to 8x² – gx – h

Thus, by comparison of terms;

– gx = - 7x

-x will cancel out to get;

g = 7

Similarly, - h = - 3

Thus,h = 3

Therefore; g = 7 and h = 3

Step-by-step explanation:

The given multi-step method is a second-order explicit method for solving ordinary differential equations. Let's analyze its properties:

Zero Stability: Zero stability refers to the property of a numerical method to produce a solution that remains bounded as the step size approaches zero. In this case, since the method is explicit, it does not involve backward recursion. Zero stability is not affected by the coefficients of the method but rather depends on the stability properties of the underlying differential equation. Therefore, we cannot make any conclusions about zero stability based solely on the given method.

Consistency: Consistency refers to the property of a numerical method that approximates the true solution of the differential equation accurately as the step size approaches zero. To check consistency, we need to compare the method with the differential equation it aims to solve. By applying Taylor series expansions to the terms in the given method, we can determine the truncation error. If the truncation error goes to zero as the step size approaches zero, the method is consistent.

Therefore, to fully assess consistency, we would need to analyze the truncation error by expanding the terms and comparing them with the original differential equation. Convergence: Convergence is the property of a numerical method where the numerical solution approaches the true solution of the differential equation as the step size approaches zero. The convergence of a method depends on both consistency and stability. If a method is consistent and stable, it is also convergent.

However, since we cannot determine the stability of the method solely based on its formulation, we cannot definitively conclude on the convergence of this specific method without further analysis. Based on the given information, we cannot determine the zero stability or convergence of the multi-step method. To assess consistency, we would need to expand the terms and compare the truncation error with the original differential equation. Further analysis is required to make conclusive statements about the properties of this method.

Learn more about term here: brainly.com/question/17142978

#SPJ11

The fewest number of swaps needed to reverse the list is  2

This is further explained below.

Generally,  In the field of computer science, a data structure known as an array sometimes referred to simply as an array, is one that is composed of a collection of items, each of which is distinguished by at least one array index or key. An array is saved in such a way that a mathematical formula may use the index tuple of each element to determine the location of that element within the array.

Given an array with values 5, 10, 15, 20, 25

Swaps did reverse the array are

Therefore, the number of swaps necessary to invert the list is two. This is the smallest possible number.

In conclusion,  Two exchanges are the bare minimum required to accomplish the list's reversal.

Read more about  Array

https://brainly.com/question/19570024

#SPJ4

Using the concepts and properties of mean and standard deviation, it is found that:

-------------------

In this problem:

A similar problem is given at https://brainly.com/question/20640860

Answer:

Nalani is correct.

Step-by-step explanation:

Given - Nalani says the expression 9+7r cannot be factored using the GCF.

To find - Is she ​correct? Explain why or why not.

Proof -

GCF - Greater Common factor

Given that, the expression is - 9 + 7r

As

HCF(9, 7) = 1

So , we can not factor the expression.

i.e. there does not exist any number who is a multiple of 9 and 7 both.

So,

Nalani is correct.

Example -

Let the expression be 24 + 18x

HCF(24, 18) = 6

So,

24 + 18x = 6(4 + 3x)

The probability comes out to be 0.2296

We need to calculate the probability of each jet waiting at least 10 minutes before takeoff.

P(X≥10)=?

Let Z be the standard normal variable.

Z=(X-μ)/σ

Where μ is the mean of the taxi and take-off time for commercial jets and σ is the standard deviation of the taxi and takeoff time for commercial jets.

Z=(X-8.3)/2.3

Using the z-score formula, Z=(X-μ)/σ, we can standardize the value of the variable X to get its respective z-score value, z.

With a mean of 8.3 and a standard deviation of 2.3, the standardized score for a taxi and takeoff time of 10 is:

z=(10-8.3)/2.3 = 0.73913

The probability of a jet waiting at least 10 minutes before takeoff can be calculated as follows:

P(X≥10) = P(Z≥0.73913)

The probability of a standard normal random variable z is greater than or equal to 0.73913 is:

1 - Φ(0.73913)

where Φ(z) is the standard normal distribution function.

Using a standard normal distribution table or calculator, we find that:

Φ(0.73913) = 0.7704

Therefore: P(X≥10) = P(Z≥0.73913)= 1 - Φ(0.73913)= 1 - 0.7704= 0.2296

Thus, the probability of each jet waiting at least 10 minutes before takeoff is 0.2296.

Learn more about z-score:

https://brainly.com/question/31871890

#SPJ11

The 715 cm² area of the disc and the ±5 cm² error tolerance, gives;

a) x = √(715/π) cm

b) The range for the radius is; [√(710/π) cm, √(720/π) cm]

c)

f(x) = π•x²

L = 715 cm²

E = 5 cm

d = √(5/π) cm

Area of the circular metal disk = 715 cm²

a) Required; The disk radius

Let A represent the area of the disk and let x represent the radius, we have;

A = π•x²

Therefore;

x = √(A/π)

Which gives;

x = √(715/π) cm

b) Allowed area error tolerance = ± 5 cm²

The allowed range of values for the area is therefore;

Which gives;

√(710/π) ≤ x ≤ √(720/π)

c) From the \( \epsilon / \delta \) definition of limits, we have;

\( \lim\limits_{x → √(715/π)} f(x) = 715 \)

Which gives;

f(x) = A = π•x²

L = 715

|f(x) - L| < E = 5 cm

|x - √(715/π)| < d = √(5/π)

Learn more about the properties of limits here:

https://brainly.com/question/13233499

#SPJ1

5% is the interest ​ rate.

What does the term "simple interest" mean?

P = $5000

T = 4 Year

S.I. = $1000

R = ?

According to question,

                  S.I. = P * R* T/100

                 1000 = 5000 * R * 4/100

                  R = 1000 * 100/5000 * 4

                   R    =  5%

Learn more about Simple interest

brainly.com/question/25845758

#SPJ4

7/4 can be expressed as

3/4 can be expressed as

Then, the fractions to compare are:

14/8, 4/8, 7/8, 6/8

We can order them only considering the numerators. from least to greatest value the ordered list is:

4/8, 6/8, 7/8, 14/8

or

4/8, 3/4, 7/8, 7/4

Let t be the number of times a sheet of paper is folded. At first, there will be two layers of paper since it is folded only once.

However, when the same sheet is repeatedly folded in half, the number of layers of the paper keeps increasing by two. Thus, the number of layers of the paper can be expressed as: 2, 4, 8, 16, ...., 2t. The formula for finding the number of layers of paper when the original sheet is folded l times can be expressed as:

r = 2l.

The above expression shows the number of layers when the sheet is folded l times. If we have to find the expression for the number of layers for n folds, then the formula would be:

r = 2n.

Therefore, the equation that represents the number of layers of paper that result when the original sheet of paper is folded a total of l times is r = 2l.

To learn more about expression visit:

brainly.com/question/28172855

#SPJ11

a) The relationship between b and c is that c cannot be zero.

b) b can be any nonzero constant and c is equal to 2.5 in this case.

In two dimensions, the compatibility equations for strain are,0

∂εx/∂y + ∂γxy/∂x = 0

∂εy/∂x + ∂γxy/∂y = 0

where εx and εy are the normal strains in the x and y directions, respectively, and γxy is the shear strain.

Using the given strain field, we can calculate the strains,

εx = -4.5cx² + 10.5cy

εy = 1.5cx² - 7.5cy²

γxy = 1.5bxy

Taking partial derivatives and plugging them into the compatibility equations, we get,

⇒ -9cx + 0 = 0

⇒ 0 + (-15cy) = 0

These equations must be satisfied for the strain field to be compatible. From the first equation,

We get cx = 0, which means c cannot be zero.

From the second equation, we get cy = 0,

Which means b can be any nonzero constant.

For part b:

We are asked to find the displacements u and v corresponding to the given strain field at points (3, 7), assuming they are zero at point (0, 0) and using c = 2.5.

To find the displacement components,

We need to integrate the strains with respect to x and y. We get,

u = ∫∫εx dx dy = ∫(10.5cy) dy = 5.25cy²

v = ∫∫εy dx dy = ∫(1.5cx² ) dx - ∫(7.5cy²) dy = 0.5cx³ - 2.5cy³

Plugging in the values of c and b, we get,

u = 5.25(2.5)(7)²  = 767.62

v = 0.5(2.5)(3)³ - 2.5(7)³ = -8583.75

Therefore,

The displacements at points (3, 7) are u = 767.62 and v = -8583.75.

To learn more about derivatives visit;

https://brainly.com/question/29144258

#SPJ4

Answer:

I thank it would be 10 and 5

Step-by-step explanation:

I hope this helps

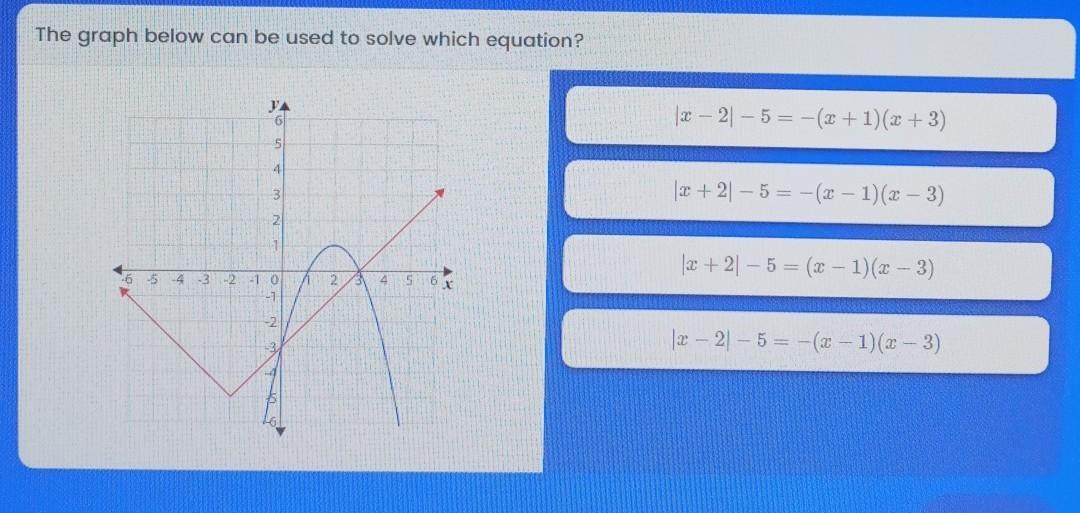
Answer:

Step-by-step explanation:

3

Answer:

I believe the answer is $1,742.12

Sorry if im wrong!

Answer:

m = 32

Step-by-step explanation:

-4(2m-7) = 3(52 - 4m)

-8m + 28 = 156 - 12m

-8m + 12m = 156 - 28

4m = 128

m = 32 Ans...

The required solution is m = 32 to the given equation −4(2m − 7) = 3(52 − 4m).

Arithmetic operations can also be specified by subtracting, dividing, and multiplying built-in functions.

The equation is defined as mathematical statements that have a minimum of two terms containing variables or numbers that are equal.

We have been given an equation as

⇒ -4(2m-7) = 3(52 - 4m)

Apply the distributive of multiplication,

⇒ -8m + 28 = 156 - 12m

Rearrange the terms of m in the above equation,

⇒ -8m + 12m = 156 - 28

Apply the subtraction operation,

⇒ 4m = 128

Divided by 4 both sides of the equation, we get

⇒ m = 32

Therefore, the solution is m = 32 to the given equation −4(2m − 7) = 3(52 − 4m).

Learn more about the equation here:

brainly.com/question/13947055

#SPJ2

Answer:

\(7\sqrt{2}\)

Step-by-step explanation:

Use trigonometry.

sin 45 degrees = x/14

plug in values and you get x = \(7\sqrt{2}\)

Answer:

72

Step-by-step explanation:

Answer:

1 inch

Step-by-step explanation:

Answer:

B

Step-by-step explanation:

using the rule of radicals

\(\sqrt{\frac{a}{b} }\) × \(\sqrt{\frac{c}{d} }\) = \(\sqrt{\frac{ab}{cd} }\) , then

\(\sqrt{\frac{3x}{2} }\) × \(\sqrt{\frac{x}{6} }\)

= \(\sqrt{\frac{3x^2}{12} }\)

= \(\sqrt{\frac{3x^2}{3(4)} }\)

= \(\sqrt{\frac{x^2}{4} }\)

= \(\frac{\sqrt{x^2} }{\sqrt{4} }\)

= \(\frac{x}{2}\)

Answer:

Approximately 34.66 feet.

Step-by-step explanation:

Pythagorean theorem states that the side lengths of a triangle can be found with A² + B² = C². For the value of A, we will use 24. For the value of B, we will use 25. 24² is 576. 25² is 625. If you add 576 and 625, you get 1201. Then, you find the square root of 1201. That is approximately 34.66. 34.66 ft. is the length of the final side.

Answer:

$ 251,619.37        

Step-by-step explanation:

Given that :

Loan = $ 268,000

Interest rate = 4.4 % per annum

4.4%/12 months =   0.366% per month

\($3/27$\) : \($3$\) years to pay and \(27\) years amortization

\(27\) years x 12 months = \(324\) months

Calculating the amount for he monthly amortization,

\($A=P \times \frac{r(1+r)^n}{(1+r)^n-1}$\)

\($A=268,000 \times \frac{0.00366(1+0.0366)^{324}}{(1+0.00366)^{324}-1}$\)

\($A=268,000 \times \frac{0.0119}{2.266}$\)

A = 1407.41

Therefore, the future value is given by :

\($FV=PV(1+r)^n-P\left[\frac{(1+r)^n-1}{r}\right]$\)

where, FV = future value ( balloon balance)

            PV = present value (original balance)

            P = payment

            r = rate per payment

            n = number of payments

\($FV=268,000(1+0.00366)^{36}-1407.41\left[\frac{(1+0.00366)^{36}-1}{0.00366}\right]$\)

\($FV = 305670.10- 54050.73 $\)

FV = 251619.37

Therefore, Stuart's balloon payment will be $ 251,619.37

9514 1404 393

Answer:

  y = 2(x +2)(x -4)

Step-by-step explanation:

The y-intercept will be a constant times the product of the roots. Here, the product of the roots is (-2)(4) = -8, so the constant of interest is -16/-8 = 2. That constant is the coefficient of the leading term of the quadratic, so is a multiplier of the factored form.

  y = 2(x +2)(x -4)

__

For root p, (x-p) is a factor in the factored form.

Answer:

Henish will have 5-1 foot pieces.

Step-by-step explanation:

If I understand the question, it is divided by five to get the pieces.

Answer:

Mean - 84

Median - 77

Mode - 84, 96, 72, 77, 91 (Or no mode)

Range - 12

Step-by-step explanation:

Mean;

Step 1 - Add all the numbers up:

84 + 96 + 72 + 77 + 91

= 420

Step 2 - divide that by 5 (because there are 5 numbers):

420 ÷ 5

= 84

Median;

Step 1 - Put the numbers in order:
84, 72, 77, 91, 96

Step 2 - Find the middle number

84, 72, 77, 91, 96

Mode;

There aren't any repeated numbers so you can put all the numbers or no mode

84, 96, 72, 77, 91

Range;

Step 1 - Subtract the smallest number from the biggest number:

96 - 84

= 12

You're welcome :)

Answer: |p-72% |≤ 4%

Step-by-step explanation:

Let p be the population proportion.

The absolute inequality about p using an absolute value inequality.:

\(|p-\hat{p}| \leq E\) , where E = margin of error, \(\hat{p}\) = sample proportion

Given:  A poll result of 72% with a margin of error of 4% indicates that p is most likely to be between 68% and 76% .

|p-72% |≤ 4%

⇒    72% - 4% ≤ p ≤ 72% +4%

⇒  68%  ≤ p ≤  76%.

i.e. p is most likely to be between 68% and 76% (.

The conclusion about p using an absolute value inequality is in the range of 29.8% to 34.2%.

An expression using absolute functions and inequality signs is known as an absolute value inequality.

We know that the absolute value inequality about p using an absolute value inequality is written as,

\(|p-\hat p| \leq E\)

where E is the margin of error and \(\hat p\) is the sample proportion.

Now, it is given that the poll result of 72% with a margin of error of 4% indicates that p is most likely to be between 68% and 76%. Therefore, p can be written as,

\(|p-0.72|\leq 0.04\\\\(0.72-0.04)\leq p \leq (0.72+0.04)\\\\0.68 \leq p\leq 0.76\)

Thus, the p is most likely to be between the range of 68% to 76%.

Similarly, the proportion of people who like dark chocolate more than milk chocolate was 32% with a margin of error of 2.2%. Therefore, p can be written as,

\(|p-\hat p|\leq E\\\\|p-0.32|\leq 0.022\\\\(0.32-0.022)\leq p \leq (0.32+0.022)\\\\0.298\leq p\leq 0.342\)

Thus, the p is most likely to be between the range of 29.8% to 34.2%.

Hence, the conclusion about p using an absolute value inequality is in the range of 29.8% to 34.2%.

Learn more about Absolute Value Inequality:

https://brainly.com/question/4688732

Step-by-step explanation:

j = jana's age

m = mom's age = 2.5 j

g = grandma's age = 5.25 j      summed, they equal 149 IN THREE YEARS

j+3       +     2.5j +3     +    5.25 j + 3 = 149

8.75 j  + 9 = 149

8.75 j = 140

j = 16  y/o

   mom = 2.5 j = 40 y/o

         g-ma = 5.25 j = 84 y/o

Therefore, the value of n that makes the system of equations true is n = 10.

Given:

p = 2n

p - 5 = 1.5n

Substituting the value of p from the first equation into the second equation, we have:

2n - 5 = 1.5n

Next, we can solve for n by subtracting 1.5n from both sides of the equation:

2n - 1.5n - 5 = 0.5n - 5

Simplifying further:

0.5n - 5 = 0

Adding 5 to both sides of the equation:

0.5n = 5

Dividing both sides by 0.5:

n = 10

Therefore, the value of n that makes the system of equations true is n = 10.

Learn more about equations here

https://brainly.com/question/29657992

#SPJ11

L((7,8)) = (-9,23).  To find the value of L((7,8)), we can use the linearity property of the linear operator L.

Since L is a linear operator, we can express any vector in R² as a linear combination of the basis vectors (1,0) and (0,1).

We have L((1,2)) = (-2,3) and L((1,-1)) = (5,2). Therefore, we can express (7,8) as (7,8) = 7(1,2) + 1(1,-1).

Using the linearity property, we can distribute the linear operator L over the linear combination:

L((7,8)) = L(7(1,2) + 1(1,-1))

= 7L((1,2)) + L((1,-1))

= 7(-2,3) + (5,2)

= (-14,21) + (5,2)

= (-9,23)

Know more about linearity property here:

https://brainly.com/question/28709894

#SPJ11

Answer:

6 ft. 1 in.

Step-by-step explanation:

There are 12 inches in a foot.

Divide 73 by 12