A ladder leans against the wall at the point B
(window end) from a ground level and makes an
angle horizontally at 52º. The height of ladder is 15
m. When the same ladder leans above the point B
at point A (window start) and makes an angle of 85°
horizontally. The distance between point A and
point B is
Answers
Answer:
..........
Step-by-step explanation:
Given:
The height of the ladder = 15 m
When the ladder leans at point B from the ground level, then it makes an angle of 52° with the horizontal
When the ladder leans at point A from the ground level, then it makes an angle of 85° with the horizontal
To find:
The distance between point A and point B is?
Solution:
To solve the above-given problem, we will use the following trigonometric ratio of a triangle:
Referring to the figure attached below, we will assume,
BD = AD = 15 m = height of the ladder
∠BDC = 52° = angle of elevation to the foot of the window
∠ADC = 85° = angle of elevation to the top of the window
Now,
In ΔBCD, we have
Opposite side = BC
Hypotenuse = BD = 15 m
θ = 52°
∴
and
In ΔACD, we have
Opposite side = AC
Hypotenuse = AD = 15 m
θ = 85°
∴
∴ The height of the window, AB = AC - BC = 14.94 m - 11.82 m = 3.12 m
Thus, the distance between point A and point B is 3.12 m.
-----------------------------------------------------------------------------------------------
Also View:
A ladder leaning against a wall makes an angle of 60 degree with the horizontal If the foot of the ladder is 2.5 m away from the wall , find the length of the ladder.
Related Questions
A math test has 25 multiple choice questions. Each question has 4 possible answers.
Which is the best way to simulate getting a 100% on this test?
Answers
GET THEM ALL RIGHT!?
PLZ HELP ME
If line p is parallel to line q what is the measure of angle EFG

Answers
Answer:
i think x=3
Step-by-step explanation:
5x+14=19x-28
- 14=19x−28−5x
- 14+28=14x
- 42=14x
(divide)
x=3
{2} is an element of the set (x € RX is an interger greater than 13 True False
Answers
The statement is false because the element 2 does not meet the criteria of being an integer greater than 13.
To determine if {2} is an element of the set of integers greater than 13, we need to analyze the statement.
The set of integers greater than 13 can be represented as {x | x ∈ ℤ, x > 13}. This set contains all integers that are greater than 13.
Now, let's check if the element 2 is in this set. Since 2 is not greater than 13, it does not satisfy the condition x > 13. Therefore, {2} is not an element of the set of integers greater than 13.
Learn more About element from the given link
https://brainly.com/question/20096027
#SPJ11
What is the value of x?
x =

Answers
Answer:
141
Step-by-step explanation:
It is a 7 sided shape
first find the sum of interior angles
7-2 x 180 = 900
so 122 +125 +131 +107+ x-15+x+x+7 = 900
477 +3x =900
3x= 423
x=141
It costs $15 to send 3 packages through a certain shipping company. Consider the number of packages per dollar
Answers
It Is Going To Be 5 Because 15÷3=5 And 15÷5=3 And 5×3=15 3×5=15
how much can 18 go to 80
Answers
18 can go into 80 four times
Hope my answer helped u :)
therefore: 18 can go into 80 4.4 times
Please help ASAP I hate maths and am so confused

Answers
Answer:
90 i think im sorry if its wrong
Step-by-step explanation:
Pls just give coordinates i will give brainliest

Answers
Answer:
(-2,2) see attached diagram
Step-by-step explanation:
see graph

Solve x2 - 16x + 60 = -12 by completing the steps. First, subtract 60 from each side of the equation. Next, add 8 ⇒ 64 to each side of the equation to complete the square. Now, write x² - 16x + 64 = -8 as ✔ (x - 8)² = -8 Take the square root of both sides to get the solutions
Answers
Answer:
Step-by-step explanation:
Given x^2 - 16x + 60 = -12
Using the completing the square method to find x;
subtract 60 from both sides
x2 - 16x + 60-60 = -12-60
x2 - 16x = -72
Add square of the half of the coefficient of x to both sides
x2 - 16x + (1/2(-16))² = -72 + (1/2(-16))²
x^2 - 16x +64 = -72+64
(x-8)² = -8
Take the square root of both sides
√(x-8)² = √-8
x - 8 = ±√8i
x = ±√8i+8
x = ±2√2i+8
The solution of the given equation is: \(x = 8+\sqrt{-8}\) and \(\\x = 8-\sqrt{-8}\).
Given that:
Equation: \(x^2 - 16x + 60 = -12\)
Simplify the above equation as:
x² - 16x + 60 = -12
x² - 16x = -12 - 60
x² - 16x = -72
Add 64 to each side of the equation to complete the square.
x² - 16x + 64 = -72 + 64
x² - 16x + 64 = -8
Write x² - 16x + 64 as (x - 8)² since it is a perfect square trinomial.
(x - 8)² = -8
Take the square root of both sides to get the solutions.
\(x - 8 = \±\sqrt{-8}\\x = 8\±\sqrt{-8}\\x = 8+\sqrt{-8}\\x = 8-\sqrt{-8}\)
where i is the imaginary unit.
Hence, the value of x are: \(x = 8+\sqrt{-8}\) and \(\\x = 8-\sqrt{-8}\).
Learn more about Equation here:
https://brainly.com/question/29657983
#SPJ6
▸
People attending a basketball game either supported the home team or the visiting
team. If 2940 of the people attending supported the home team and 560 supported
the visiting team, what percentage supported the home team?
Answers
Answer:
84%
Step-by-step explanation:
2940+560=3,500
\(\frac{2940*100}{3500} =\)\(\frac{84}{100}\)
=84%
v=2/3 ayuda porfavooooor

Answers
Answer: answer is a
Step-by-step explanation:
there is some indication in medical litera- ture that doctors may have become more aggressive in inducing labor or doing preterm cesarean sections when a woman is carrying twins. records at a large hospital show that, of the 43 sets of twins born in 1990, 20 were delivered before the 37th week of pregnancy. in 2000, 26 of 48 sets of twins were born preterm. does this indicate an increase in the incidence of early births of twins? test an appropriate hypothesis and state your conclusion.
Answers
The given data can be used to test the hypothesis that the proportion of preterm births among twins has increased from 1990 to 2000 and the conclusion is that the proportion of preterm births among twins has increased from 1990 to 2000.
Using a two-proportion z-test, with the null hypothesis that the proportions are equal, we find that the test statistic is approximately 1.89, with a p-value of 0.029. This suggests that there is evidence to reject the null hypothesis at the 5% significance level, and conclude that the proportion of preterm births among twins has increased from 1990 to 2000.
However, it's important to note that this conclusion is based on the assumption that the two samples are independent and representative of the population of interest. Other factors, such as changes in the population or hospital policies, may have also contributed to the observed increase in preterm births among twins.
To know more on two-proportion z-test
https://brainly.com/question/30762753
#SPJ4
5
w is an integer such that 6 < 3w < 18
x is an integer such that -4 < x < 3
(a) Work out all the possible values of w
Answers
Answer:
W can be 3, 4, and 5
Step-by-step explanation:
If it is less than 18 and higher than 6 then I think those, 3 times 3, 4, and 5, would be in between your range.
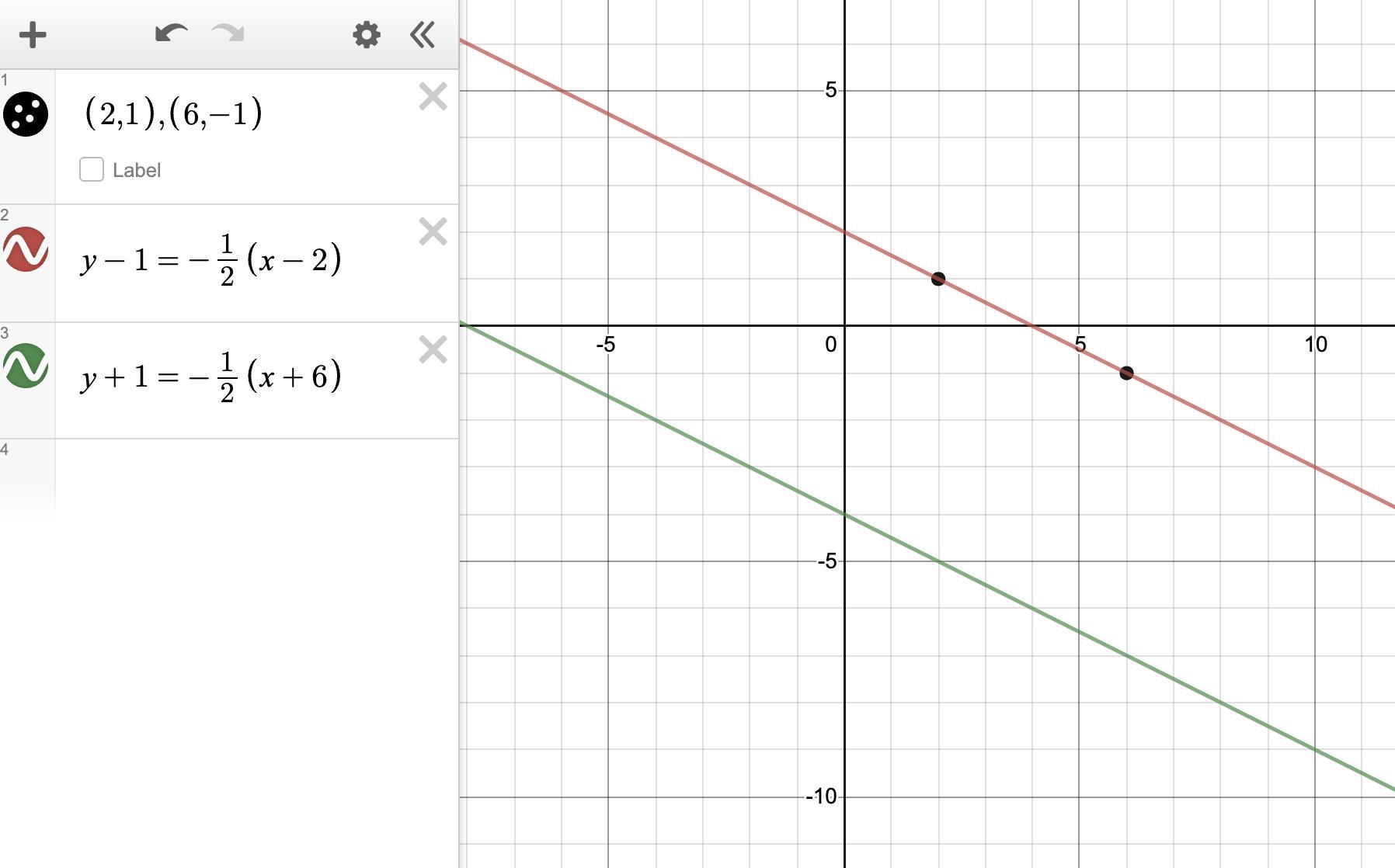
Which of the following equations is parallel to, but not the same as, the line that passes through
the points (2, 1) and (6, -1)?
(1) y = 1/2x - 2
(2) y-1 = -1/2(x - 2)
(3) y + 1 = -1/2(x + 6)
(4) y = 1/2x-1
Answers
9514 1404 393
Answer:
(3) y + 1 = -1/2(x + 6)
Step-by-step explanation:
The slope of the line between the two points can be found from the slope formula:
m = (y2 -y1)/(x2 -x1)
m = (-1 -1)/(6 -2) = -2/4 = -1/2
Then the point-slope form of the equation of the line through the given points can be written as either of ...
y -1 = -1/2(x -2)
y +1 = -1/2(x -6)
We note that only choices (2) and (3) have slopes of -1/2, so are parallel. Choice (2) matches the first equation above, so is the identical line, not one that is parallel.
Choice (3) matches neither of the equations of the line through the given point, so that is the choice of interest.
Find the profit margin on ladders that were purchased for $65.00 each, and now sell
for $105.99 each. Round to nearest hundredths. (Hint: This is a two-step problem.)
Answers
105.99 - 65.00 / 105.99
profit = 40.99
40.99 / 105.99 = 0.38673
profit margin = 38.673%
which of the following run-time complexity orders ranks between the other two? group of answer choices o(2^n) exponential none of these o(n^2) quadratic (or polynomial) o(log n) logarithmic time
Answers
As per the question, the complexity that ranks between the other two is O(n^2) - Quadratic (or Polynomial).
How to solveAs we compare the run-time complexities, it's crucial to examine the function’s growth with an increase in input size (n).
Let us analyze the growth rates:
Exponential (O(2^n)): The function doubles for each increment in n. This is very fast growth.
Quadratic (O(n^2)): The function grows proportional to the square of n. This is slower growth compared to exponential but faster than logarithmic.
Logarithmic (O(log n)): The function grows very slowly as n increases. The growth rate is less than linear (O(n)).
So the ranking, from slowest to fastest growth, is:
O(log n) - Logarithmic
O(n^2) - Quadratic (or Polynomial)
O(2^n) - Exponential
As per the question, the complexity that ranks between the other two is O(n^2) - Quadratic (or Polynomial).
Read more about quadratic run-time complexity here:
https://brainly.com/question/24488401
#SPJ1

suppose i draw from the population at random with replacement. what is the chance that at least one-third of my first 30 draws are successful?
Answers
The probability that all 3 cards are clubs will be 0.0129
To find the chance that all three cards are clubs,
We can use the following formula:
\(P(\text{all 3 are clubs}) = \frac{\text{number of favorable outcomes}}{\text{number of possible outcomes}}\)
The number of favorable outcomes is the number of ways to choose 3 clubs from the 13 clubs in the deck, which is given by the given binomial coefficient \({13 \choose 3} = 286\)
The number of possible outcomes is the number of ways to choose 3 cards from the deck, which is given by the binomial coefficient \({52 \choose 3} = 22,!100\)
Therefore, the value of the probability that all 3 cards are clubs is:
\(P(\text{all 3 are clubs}) = \frac{\text{number of favorable outcomes}}{\text{number of possible outcomes}} \\= \frac{286}{22,!100} \\\approx 0.0129\)
Rounding to 3 decimal places, the answer is 0.013.
For more questions on Probability
https://brainly.com/question/25870256
#SPJ4
The complete questions should be:
A standard deck of cards has 52 cards. There are 4 suits clubs, diamonds, hearts, and spades each of which has 13 cards. Suppose you draw 3 cards without replacement. What is the chance that all three are clubs? Round your answer to 3 decimal places
Write a system of linear equations in which (2, -1) is a solution of equation 1 but
not a solution of equation 2, and (5, 5) is a solution of the system. then solve the
system by substitution to verify that (5, 5) is the solution.
Answers
The sytem of liner equation are that satisfies the given conditon are:
L1 : 2x-y=5
L2 : 3x - y = 10
Given that one of the line of the sytem of equations passes through (2,-1) and also given that solution of system of equations is (5,5) so it justifies that the 1st line passes through (2.-1) and (5,5) so the equation of 1st line is given by:
To find the equation of a line that passes through the points (2, -1) and (5, 5), we can use the point-slope form of a line, which is:
y - y1 = m(x - x1)
where (x1, y1) is a point on the line, and m is the slope of the line.
To find the slope of the line, we can use the formula:
m = (y2 - y1) / (x2 - x1)
Substituting the coordinates of the two given points and the formula for the slope into the point-slope form, we get:
y - (-1) = ((5 +1) / (5 - 2))(x - 2)
= (6 / 3)(x - 2)
= 2(x - 2)
= 2x - 4
=> 2x- y =5
so the equation of line 1 is 2x-y=5
And as mentioned that equation of line that passes through (5,5) but as given it won't pass through (2,-1)
so let m be the slope of 2nd line and passes through (5,5)
so the equation of line is given by:
y-5 = m (x-5)
and if this line won't pass through (2,-1) then
-1 - 5 ≠ m (2 -5)
m ≠ 2
so the equation of 2nd line is given by:
y - 5 = 3(x-5)
=> 3x - y = 10
So the equation of sytem of liner equation are
L1 : 2x-y=5
L2 : 3x - y = 10
To know more about linear equation click on below link:
https://brainly.com/question/11897796#
#SPJ4
The rectangular floor of a classroom is 30 feet in length and 20 feet in width. A scale drawing of the floor has a length of 15 inches. What is the area, in square inches, of the floor in the scale drawing?
HURRY PLEASEEEEEEEE
Answers
The area of the floor in the scale drawing will be equal to 150 in².
What is the area?An object's area is how much space it takes up in two dimensions. It is the measurement of the number of unit squares that completely encompass the surface of a compact figure. The squared unit, which is frequently expressed as inches, square feet, etc., is the accepted unit of area.
As per the given information in the question,
Length of the classroom, l = 30 feet and,
The width of the classroom, w = 20 feet.
As per the scale drawing, the length of the classroom, l' = 15 feet
Let the scale width, w' = x feet
As we can see that the original length is twice the scale drawing.
Then, the original width also is twice the scale drawing.
So, w' = 20/2 = 10 feet.
Now, the area of the floor in the scale drawing will be,
A = wl
A = (15)(10)
A = 150 in².
To know more about Area:
https://brainly.com/question/27683633
#SPJ1
Help help urgently now ❤️That’splease please



Answers
Answer:
6566
Step-by-step explanation:
The answer is 6566.
Can someone please help me please I really need help please help me.

Answers
Answer:
Step-by-step explanation:
I can't get to act correctly either.
The answer is 1 day and 7 items.
Ariana
y = 5x + 2
Julie
y = 7x
The ys have to be the same so equate the right hand side.
7x = 5x + 2 Subtract 5x from both sides.
7x - 5x = 5x - 5x + 2
2x = 2 Divide by 2
2x/2 = 2/2
x = 1
1 day
7 items
Lisa is measuring the depth of a well. She drops a ball from a height of h feet into the well and measures how long it takes the ball to hit the bottom of the well. The polynomial -16 t 2 0t h models this situation, where 0 is the initial speed of the ball and h is the height it was dropped from. (This is a different well from the problem you solved before.) She raises her arm very high and drops the ball from a height of 6.0 feet. Her stopwatch measured a time of 3.5 seconds. How deep is the well
Answers
The depth of the well is 190 feet.
Given that Lisa raises her arm very high and drops a ball from a height of 6.0 feet. Her stopwatch measured a time of 3.5 seconds. And the polynomial equation that models this situation is -16t² + 0t + h, where h is the height from which the ball was dropped. So we need to find the value of h. Using the formula, h = -16t² + 0t + h Substituting the given values, we get h = -16 × 3.5² + 0 × 3.5 + 6h = -196 + 6h = -190 feet.
Therefore, the depth of the well is 190 feet.
To learn more about depth here:
brainly.com/question/13804949#
#SPJ11
Tony goes into Dave's Army-Navy store and buys a hat for $14. He gives Dave a $20 bill. Dave doesn't have any change, so he takes the $20 bill across the street to Laura, the clerk in Watson's Hardware store. Laura trades Dave's $20 bill for twenty $1 bills. Dave comes back and gives Tony $6 in change. Tony takes the hat and the $6 and leaves town forever. Half an hour later Laura comes over to Dave's store, just furious. She has discovered that the $20 bill he gave her is counterfeit. Dave, of course, makes it good, giving Laura a genuine $20 bill he has in the till from earlier.
Question: Now that it is all over, who came out behind? And by how much? Explain
Answers
In this scenario, Tony is the one who comes out behind, and by $14. Tony's loss of $14 is smaller than Dave's loss of $20, making Tony the one who comes out behind by a smaller amount.
Tony initially purchases a hat for $14 and gives Dave a $20 bill. Since Dave doesn't have any change, he goes to Laura at Watson's Hardware store and exchanges the $20 bill for twenty $1 bills. Dave gives Tony $6 in change, which means Tony effectively paid $8 for the hat ($14 - $6).
However, it is later discovered that the $20 bill given to Laura by Dave was counterfeit. As a result, Dave compensates Laura by giving her a genuine $20 bill from the store's till. This means that Dave essentially lost $20 in the process.
So, in total, Tony ends up $14 behind because he paid $8 for the hat and received $6 in change, while Dave ends up $20 behind due to the counterfeit $20 bill. Tony's loss of $14 is smaller than Dave's loss of $20, making Tony the one who comes out behind by a smaller amount.
To learn more about smaller amount click here : brainly.com/question/30837774
#SPJ11
Below shows the academic level values of the data set in (c). Apply formulas to calculate the average number of publications per faculty. unit Mi Yi 6 62 2.25
9 48 0.25
11 41 5.50
14 65 1.75
16 10 0.50 19 62 1.25 21 61 2.00
23 25 1.25
14 65 0.75
14 65 1.00 If the first stage is PPS without replacement. What is the inclusion probability for unit 6 (PSU level)?
Answers
To calculate the inclusion probability for unit 6 (PSU level) in the first stage of PPS without replacement, we need to divide the number of sampling units in the population by the total number of sampling units selected in the first stage.
Looking at the provided data, we can see that there are a total of 10 sampling units (Mi) in the dataset.
In PPS without replacement, the first sampling unit is selected with certainty. So, the inclusion probability for unit 6 (PSU level) is:
Inclusion probability = 1 / Total number of sampling units selected in the first stage
= 1 / 10
= 0.1
Therefore, the inclusion probability for unit 6 (PSU level) in the first stage of PPS without replacement is 0.1 or 10%.
Learn more about inclusion probability here: brainly.com/question/29264519
#SPJ11
please help!!! help plssss

Answers
Answer:
x = 14
Step-by-step explanation:
Two angles a, b are complentary if a+b = 90.
Therefore, 4x + (2x+6) = 90
6x + 6 = 90
6x = 84
x = 84/6 = 14.
Answer:
x=14°
Step-by-step explanation:
Complementary angles are angles that add to 90°.
4x+2x+6=90
add like terms
6x+6=90
subtract 6 on both sides
6x=84
divide 6 on both sides
x=14
x is 14°.
(04.05, 05.04, 07.04 HC) dy = 5(2x + 3)sin (x2 + 3x +"). x dx Consider the differential equation Part A: Find the equation of the line tangent to the solution curve at the point (0,5). (5 points) Part B: Find the second derivative at (0,5) and use it to determine the concavity of the solution curve at that point. Explain. (10 points) Part C: Find the particular solution y = f(x) with initial condition f(0) = 5. (15 points)
Answers
Part a: The equation of the tangent line is: y - 5 = -15(x - 0)
Part b:The second derivative is a constant value, -15. Since the second derivative is negative, it means the function is concave down at (0, 5).
Part c:The particular solution is y = -10cos(x² + 3x + π) + 15(x² + 3x + π) - 5 - 15π
Part A: To find the equation of the line tangent to the solution curve at the point (0, 5), to follow these steps:
Step 1: Find the derivative of the given differential equation.
Given differential equation: dy/dx = 5(2x + 3)sin(x² + 3x + π)
Differentiate both sides with respect to x:
dy/dx = d/dx (5(2x + 3)sin(x²+ 3x + π))
dy/dx = 5 × (2(sin(x² + 3x + π)) + (2x + 3)cos(x² + 3x + π))
Step 2: Evaluate the derivative at the point (0, 5).
To find the slope of the tangent line at (0, 5), substitute x = 0 into the derivative:
dy/dx = 5 × (2(sin(π)) + (2×0 + 3)cos(π))
dy/dx = 5 × (2(0) + 3(-1)) = -15
Step 3: Use the point-slope form of the equation to write the equation of the tangent line.
The point-slope form of the equation is: y - y1 = m(x - x1), where m is the slope and (x1, y1) is the point (0, 5).
Simplifying, we get: y = -15x + 5
Part B: To find the second derivative at (0, 5) and determine the concavity of the solution curve at that point, follow these steps:
Step 1: Find the second derivative of the given differential equation.
Given differential equation: dy/dx = 5(2x + 3)sin(x² + 3x + π)
Differentiate the previous result for dy/dx with respect to x to get the second derivative:
d²y/dx² = d/dx (-15x + 5)
d²y/dx² = -15
Step 2: Determine the concavity.
Part C: To find the particular solution y = f(x) with the initial condition f(0) = 5, to integrate the given differential equation:
dy/dx = 5(2x + 3)sin(x² + 3x + π)
Step 1: Integrate the equation with respect to x:
∫dy = ∫5(2x + 3)sin(x² + 3x + π) dx
y = ∫(10x + 15)sin(x² + 3x + π) dx
Step 2: Use u-substitution:
Let u = x² + 3x + π, then du = (2x + 3) dx
Now the integral becomes:
y = ∫(10x + 15)sin(u) du
Step 3: Integrate with respect to u:
y = -10cos(u) + 15u + C
Step 4: Substitute back for u:
y = -10cos(x² + 3x + π) + 15(x² + 3x + π) + C
Step 5: Apply the initial condition f(0) = 5:
Substitute x = 0 and y = 5 into the equation:
5 = -10cos(π) + 15(0² + 3(0) + π) + C
5 = 10 + 15π + C
Simplifying,
C = 5 - 10 - 15π
C = -5 - 15π
To know more about equation here
https://brainly.com/question/29657983
#SPJ4
Explain why the denominator 6 in 3/6 is not changed when adding fractions
Answers
The denominator 6 in 3/6 is should not be changed when adding fractions if other fractions have a denominator of 6, to make the addition easy because 6 will be the lowest common multiple.
Why are denominators not changed when adding fractions?
One of the reasons why the denominator will always stay the same when adding fraction is because the size of the equal pieces does not change when you combine the two fractions together.
For example say you want to add 3/6 + 1/6 + 2/6,
you will notice that all the fractions have equal denominator, so adding the fractions together will have the following result.
3/6 + 1/6 + 2/6 = (3 + 1 + 2 ) / 6
= 6/6
= 1
So the 6 in 3/6 should not be changed if all other fractions you wish to add to 3/6 have 6 as their denominator, because the 6 is lowest common multiple.
Learn more about addition of fractions here: https://brainly.com/question/78672
#SPJ1
Please help me on this

Answers
The solution to the limits (a) and (b) are 24 and 4 respectively.
Understanding LimitsGiven
lim f(x)=8
lim g(x)=-2
lim h(x)=0
Using the properties of limits and basic arithmetic operations, we can find the limit of the following:
(a) \(\lim_{x \to \ 3} [2f(x) - 4g(x)]\)
We can apply the properties of limits to each term separately:
lim [2f(x)] - lim [4g(x)] as x approaches 3.
Using the given information:
2 * lim f(x) - 4 * lim g(x) as x approaches 3.
Substituting the known limits:
2 * 8 - 4 * (-2) = 16 + 8 = 24.
Therefore, lim [2f(x) - 4g(x)] as x approaches 3 is equal to 24.
(b) \(\lim_{n \to \ 3} [2g(x)^{2} ]\)
We can apply the property of limits to the entire expression:
[lim (2g(x))]² as x approaches 3.
Using the given information:
[lim g(x)]² as x approaches 3.
Substituting the known limit:
(-2)² = 4.
Therefore, lim [2g(x)]² as x approaches 3 is equal to 4.
Learn more about limit here:
https://brainly.com/question/30679261
#SPJ1
5. Problem 5.15 (Present Value of an Annuity) Find the present values of these ordinary annuities. Discounting occurs once a year. Do not round intermediate calculations. Round your answers to the nearest cent. a. $400 per year for 14 years at 14%. $ b. $200 per year for 7 years at 7%. $ c. $400 per year for 7 years at 0%. $ d. Rework previous parts assuming they are annuities due. Present value of $400 per year for 14 years at 14%:$ Present value of $200 per year for 7 years at 7% : $ Present value of $400 per year for 7 years at 0% : $
Answers
a. Present value of $400 per year for 14 years at 14%: $2,702.83
b. Present value of $200 per year for 7 years at 7%: $1,155.54
c. Present value of $400 per year for 7 years at 0%: $2,800
d. Present value of $400 per year for 14 years at 14% (annuity due): $2,943.07
Present value of $200 per year for 7 years at 7% (annuity due): $1,233.24
Present value of $400 per year for 7 years at 0% (annuity due): $2,800
To find the present values of the ordinary annuities, we can use the formula for the present value of an annuity:
PV = PMT * [(1 - (1 + r)^(-n)) / r]
Where:
PV = Present value
PMT = Payment per period
r = Interest rate per period
n = Number of periods
a. $400 per year for 14 years at 14%:
PV = $400 * [(1 - (1 + 0.14)^(-14)) / 0.14]
≈ $2,702.83
b. $200 per year for 7 years at 7%:
PV = $200 * [(1 - (1 + 0.07)^(-7)) / 0.07]
≈ $1,155.54
c. $400 per year for 7 years at 0%:
Since the interest rate is 0%, the present value is simply the total amount of payments over the 7 years:
PV = $400 * 7
= $2,800
d. Reworking previous parts assuming they are annuities due:
For annuities due, we need to adjust the formula by multiplying it by (1 + r):
a. Present value of $400 per year for 14 years at 14%:
PV = $400 * [(1 - (1 + 0.14)^(-14)) / 0.14] * (1 + 0.14)
≈ $2,943.07
b. Present value of $200 per year for 7 years at 7%:
PV = $200 * [(1 - (1 + 0.07)^(-7)) / 0.07] * (1 + 0.07)
≈ $1,233.24
c. Present value of $400 per year for 7 years at 0%:
Since the interest rate is 0%, the present value remains the same:
PV = $400 * 7
= $2,800
In conclusion:
a. Present value of $400 per year for 14 years at 14%: $2,702.83
b. Present value of $200 per year for 7 years at 7%: $1,155.54
c. Present value of $400 per year for 7 years at 0%: $2,800
d. Present value of $400 per year for 14 years at 14% (annuity due): $2,943.07
Present value of $200 per year for 7 years at 7% (annuity due): $1,233.24
Present value of $400 per year for 7 years at 0% (annuity due): $2,800
To know more about formula visit
https://brainly.com/question/867780
#SPJ11
without dividing explain how the quotient of 1/8 divided by 3/5 and (-1/8) divided by (-3/5) compare
Answers
The quotients of both are equal.