B plus 14 what do that equal to
Answers
Answer:
14b
Step-by-step explanation:
Related Questions
Sally has two bags of nuts; one with 75 % peanuts, and the other
with 16 % peanuts. To make a 8 lb bag of 31 %
peanuts, how much of each should Sally use?
Please answer ASAP
Ty! :)
Answers
Answer:
Step-by-step explanation:
(.16x+.75(8-x))/8=.31
.16x+6-.75x=2.48
-.59x+6=2.48
-.59x=-3.52
x=5.9661, y=8-x=2.0339
I don’t know how much rounding you want but 6lb of the 16% and 2lb of the 75% is pretty close.
If the speed of a bus was decreased by 20% to 48 mph, how fast was the bus going originally?
Answers
Answer:
60mphStep-by-step explanation:
If the speed of a bus was decreased by 20% to 48 mph, how fast was the bus going originally?
48 mph = 80% (100%-20%=80%)
so
48 : 80 * 100 = 60mph
---------------------
check
60 - 20% = 48
the answer is good
The area of this square is one hundred twenty-one square centimeters. What is the length of one side of this square?
Answers
Answer: 11
Step-by-step explanation:
Answer:
11 square centimeters
Step-by-step explanation:
The area of a rectangle is length times width. A square is a type of rectangle that has four equal sides, so if we know one side we know all four.
A = l x w
121 = l x w
Since we know l and w are equal we can take the square root of 121, which is 11.
Triangle XYZ is isosceles. The measure of the vertex angle, Y, is twice the measure of a base angle.
What is true about triangle XYZ? Select three options.
Angle Y is a right angle.
The measure of angle Z is 45°.
The measure of angle X is 36°.
The measure of the vertex angle is 72°.
The perpendicular bisector of Line segment X Z creates two smaller isosceles triangles.
Answers
Answer:
Angle Y is a right angle.
The measure of angle Z is 45°.
The perpendicular bisector of Line segment X Z creates two smaller isosceles triangles.
Step-by-step explanation:
both base angles are the same - x
angle Y is 2x
4x= 180 (angles in a triangle add to 180)
x=45
Y = 2x = 90
Answer:
Answer:
Angle Y is a right angle.
The measure of angle Z is 45°.
The perpendicular bisector of Line segment X Z creates two smaller isosceles triangles.
Step-by-step explanation:
both base angles are the same - x
angle Y is 2x
4x= 180 (angles in a triangle add to 180)
x=45
Y = 2x = 90
Step-by-step explanation:
A leaking pond loses 12 gallon of water in 23 hours How many gallons of water will it lose in 31 hours
Answers
Answer:
The volume of water the pond will lose in 31 hours is 17.71 gallons.
Step-by-step explanation:
Given;
Rate of water leakage, R = 12 gallon of water in 23 hours
\(R = \frac{12 \ gallons}{23 \ hours}\)
In 31 hours the volume of water leaked is calculated as;
\(V = \frac{12 \ gallons}{21 \ hours} \times 31 \ hours\\\\V = 17.71 \ gallons\)
Therefore, the volume of water the pond will lose in 31 hours is 17.71 gallons.
SOMEONE PLEASE HELP ME !
Which is the slope of the line y=-32 + 2?
Answers
Answer:
the slope is 3
Step-by-step explanation:
if AB=2(x+1) BC=3x+1 and AC=4(x+2) then find the value for X.AB,BC and AC
Answers
Answer:
Givens
AB + BC = AC
AB = 2(x + 1)
BC = 3x + 1
AC = 4(x + 2)
Substitute and Solve
AB + BC = AC
2(x + 1) + 3x + 1 = 4(x + 2) Remove the brackets on the left
2x + 2 + 3x + 1 = 4(x + 2) Collect the like terms on the left
5x + 3 = 4(x + 2) Remove the brackets on the right.
5x + 3 = 4x + 8 Subtract 4x from both sides.
5x - 4x + 3 = 8
x + 3 = 8 Subtract 3 from both sides
x =8 - 3
x = 5
Answers
AB=2(5 + 1) = 2 * 6 = 12
BC = 3x + 1 = 3*5 + 1 = 15 + 1 = 16
AC = 4(5 + 2) = 4*7 = 28
Step-by-step explanation:
A certain type of automobile battery is known to last an average of 1,150 days with a standard deviation of 40 days. If 100 of these batteries are selected, find the following probabilities for the average length of life of the selected batteries. (Round your answers to four decimal places.) A button hyperlink to the SALT program that reads: Use SALT. (a) The average is between 1,142 and 1,150. (b) The average is greater than 1,158. (c) The average is less than 950.
Answers
Answer:
a) 0.4772 = 47.72% probability that the average is between 1,142 and 1,150.
b) 0.0228 = 2.28% probability that the average is greater than 1,158.
c) 0 = 0% probability that the average is less than 950.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
A certain type of automobile battery is known to last an average of 1,150 days with a standard deviation of 40 days.
This means that \(\mu = 1150, \sigma = 40\)
Sample of 100:
This means that \(n = 100, s = \frac{40}{\sqrt{100}} = 4\)
(a) The average is between 1,142 and 1,150.
This is the pvalue of Z when X = 1150 subtracted by the pvalue of Z when X = 1142. So
X = 1150
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{1150 - 1150}{4}\)
\(Z = 0\)
\(Z = 0\) has a pvalue of 0.5
X = 1142
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{1142 - 1150}{4}\)
\(Z = -2\)
\(Z = -2\) has a pvalue of 0.0228
0.5 - 0.0228 = 0.4772
0.4772 = 47.72% probability that the average is between 1,142 and 1,150.
(b) The average is greater than 1,158.
This is 1 subtracted by the pvalue of Z when X = 1158. So
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{1158 - 1150}{4}\)
\(Z = 2\)
\(Z = 2\) has a pvalue of 0.9772
1 - 0.9772 = 0.0228
0.0228 = 2.28% probability that the average is greater than 1,158.
(c) The average is less than 950.
This is the pvalue of Z when X = 950. So
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{950 - 1150}{4}\)
\(Z = -50\)
\(Z = -50\) has a pvalue of 0
0 = 0% probability that the average is less than 950.
PRE CALC HELP NEEDED

Answers
Answer:
\(\dfrac{5e^2}{2}\)
Step-by-step explanation:
Differentiation is an algebraic process that finds the slope of a curve. At a point, the slope of a curve is the same as the slope of the tangent line to the curve at that point. Therefore, to find the slope of the line tangent to the given function, differentiate the given function.
Given function:
\(y=x^2\ln(2x)\)
Differentiate the given function using the product rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let\;$u=x^2}\)\(\textsf{Let\;$u=x^2$}\implies \dfrac{\text{d}u}{\text{d}x}=2x\)
\(\textsf{Let\;$v=\ln(2x)$}\implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{2}{2x}=\dfrac{1}{x}\)
Input the values into the product rule to differentiate the function:
\(\begin{aligned}\dfrac{\text{d}y}{\text{d}x}&=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}\\\\&=x^2 \cdot \dfrac{1}{x}+\ln(2x) \cdot 2x\\\\&=x+2x\ln(2x)\end{aligned}\)
To find the slope of the tangent line at x = e²/2, substitute x = e²/2 into the differentiated function:
\(\begin{aligned}x=\dfrac{e^2}{2}\implies \dfrac{\text{d}y}{\text{d}x}&=\dfrac{e^2}{2}+2\left(\dfrac{e^2}{2}\right)\ln\left(2 \cdot \dfrac{e^2}{2}\right)\\\\&=\dfrac{e^2}{2}+e^2\ln\left(e^2\right)\\\\&=\dfrac{e^2}{2}+2e^2\\\\&=\dfrac{5e^2}{2}\end{aligned}\)
Therefore, the slope of the line tangent to the graph of y = x²ln(2x) at the point where x = e²/2 is:
\(\boxed{\dfrac{5e^2}{2}}\)
Given that the slope is -4 and the y intercept is -4 what is the equation of the line?
Answers
Answer:
y=-4x-4
Step-by-step explanation:
y=-4x-4
y=mx+b where m=slope and b=y-intercept.
A right triangle has side lengths of 5 inches, 12 inches, and 13 inches. The triangle will be rotated 180° about a point.
What is the length of the longest side of the triangle after the rotation? Enter the answer in the box?
Answers
13in will be the longest like before .
Refer to the attachment for more observation.


The length of the longest side of the triangle after the rotation is 13 inches.
What is Right Angle?It is referred to as a right angle if the angle formed by two rays exactly equals 90 degrees, or π/2.
Ancient geometry defined a right angle as the intersection of two straight, or right, lines in relation to dimensional axes.
Given:
A right triangle has side lengths of 5 inches, 12 inches, and 13 inches.
As, we know that the longest side is the Hypotenuse which is 13 inches and the base is 12 inches and perpendicular is 5 inches.
After 180° rotation only the base and perpendicular change the longest side still remain the same.
Learn more about Right Angle here:
https://brainly.com/question/7116550
#SPJ2
A genetic experiment with peas resulted in one sample of offspring that consisted of 414 green peas and 156 yellow peas. a. Construct a 95% confidence interval to estimate of the percentage of yellow peas. b. Based on the confidence interval, do the results of the experiment appear to contradict the expectation that 25% of the offspring peas would be yellow?
Answers
a. The interval in percentage is (23.46% , 30.76%)
b. No
From the question, we have
phat = =154/(414+154)
= 0.2711
The level α is 95%
1 - α = 0.05
α/2 = 0.025
the population is bigger than 30, use z-test.
From the table, z-score for α/2 = 0.025 is z = 1.96
The error for the interval is,
E=z⋅√(( phat (1-phat))/n)
E=1.96⋅√((0.2711(1-0.2711))/568)
E=0.0365
The lower and higher limits of the interval are:
phat - E = 0.2711 - 0.0365 = 23.46%
phat + E = 0.2711 + 0.0365 = 30.76%
the 95% confidence interval to estimate the percentage of yellow is (23.46%,30.76%)
b. No, because 25% is inside the interval
Multiplication:
To determine the sum of two or more numbers, mathematicians multiply the numbers. It is a basic mathematical procedure that is widely used in daily life. Multiplication is used when we need to mix groups of like sizes. Multiplication is a representation of the underlying idea of adding the same number repeatedly. The outcome of multiplying two or more numbers is referred to as the product of those numbers, and the factors are the quantities that are multiplied. Multiplying the numbers makes it simpler to add the same number repeatedly.
Complete question:
A genetic experiment with peas resulted in one sample of offspring that consisted of 414 green peas and 154 yellow peas. a. Construct a 95% confidence interval to estimate of the percentage of yellow peas. b. It was expected that 25% of the offspring peas would be yellow. Given that the percentage of offspring yellow peas is not 25%, do the results contradict expectations? a. Construct a 95% confidence interval. Express the percentages in decimal form. nothingless thanpless than nothing (Round to three decimal places as needed.) b. Given that the percentage of offspring yellow peas is not 25%, do the results contradict expectations? No, the confidence interval includes 0.25, so the true percentage could easily equal 25% Yes, the confidence interval does not include 0.25, so the true percentage could not equal 25%
To learn more about multiplication visit: https://brainly.com/question/5992872
#SPJ1
Please help find the perimeter and area of the polygon

Answers
Prove (a) B(x+1,y)= x+y
x
B(x,y). (b) Γ(2x)= π
2 2x−1
Γ(x)Γ(x+ 2
1
).
Answers
The simplified equation is (π2 / 2) * ∫[0, ∞] (x(2x-1) * e(-x) / (Γ(x) * Γ(1 - x)) DX
a. To prove B(x+1, y) = x * B(x, y), proceed as follows.
Start with B(x+1, y) = [(x+1)! * y!] / ((x+y+2)!) (using the definition of B(x, y)).
Rewrite 1 / (x+1) to (x+y+2 - (y+1)) / (x+y+2) .
Using the formula above, express B(x+1, y) as (x+y+2) / (x+y+2) * [(x+1)! to rewrite. * y!] / ((x+y+2)!) - (y+1) / (x+y+2) * [(x+1)! * y!] / ((x+y+2) !).
Simplify the formula to (x+y+2) / (x+y+2) * B(x, y) - (y+1) / (x+y+2) * B(x, y) increase.
Simplify further to B(x, y) - (y+1) / (x+y+2) * B(x, y).
Note that B(x, y) can be expressed as (x / (x+y+1)) * B(x, y) .
Substitute this formula in the previous step to get,
x * B(x, y) - (y+1) / (x+y+2) * x * B(x, y).
x * B(x, y) - (y+1) / (x+y+2) * x * B(x, y)
= x * B(x, y)
You have now proved B(x+1, y) = x * B(x, y).
b. We wish to prove the identity Γ(2x) = ((2sin(πx))) * Γ(x) * Γ(x + 1/2).
Integrate ∫[0, ∞] (x(2x-1) * Start with dx.
Evaluating this integral using the permutation u = du is obtained.
Simplify the integral to (1/2) * Γ(x + 1/2).
Express sin(πx) as π / (Γ(x) * Γ(1 - x)).
Let the original integral be π * (2(2x-1) / π) * ∫[0, ∞] (x(2x-1) * e(-x) * (1/sin( πx) Rewrite.)) DX.
Substituting the equations,
The integral, π * (2(2x-1) / π) * ∫[0, ∞] (x(2x-1) *
We get * (π / (Γ(x) * Γ(1 - x)))) dx.
For more questions on simplified equation:
https://brainly.com/question/33148611
#SPJ8
helpppp...........................

Answers
Answer:
see explanation
Step-by-step explanation:
the sum of the interior angles of a polygon is
sum = 180° (n - 2) ← n is the number of sides
a hexagon has 6 sides , then
sum = 180° × (6 - 2) = 180° × 4 = 720°
12
the polygon has 5 sides , so
sum = 180° × (5 - 2) = 180° × 3 = 540°
sum the interior angles and equate to 540
y + 90 + 120 + 90 + 110 = 540
y + 410 = 540 ( subtract 410 from both sides )
y = 130
13
the polygon has 7 sides , so
sum = 180° × (7 - 2) = 180° × 5 = 900°
sum the interior angles and equate to 900
p + 90 + 141 + 130 + 136 + 123 + 140 = 900
p + 760 = 900 ( subtract 760 from both sides )
p = 140
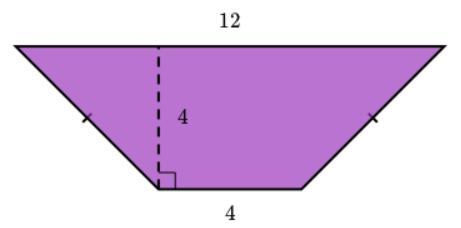
Find the area of the shape shown below.
Answers
Answer:
The answer is 32
Step-by-step explanation:
The formula for finding the area of a trapezoid is:
((base 1 + base 2)/ 2 )* h
Now all you have to do is substitute the numbers in.
Note: bases will always be the ones like 12 and 4 in this case. We have just named then 1 and 2.
Answer:
32 square units
Step-by-step explanation:
\(\displaystyle A=\frac{1}{2}(b_1+b_2)h=\frac{1}{2}(12+4)(4)=\frac{1}{2}(16)(4)=\frac{1}{2}(64)=32\)
Note that \(b_1\) and \(b_2\) are the lengths of each base of the trapezoid, so it doesn't matter which is which.
Keep the radius the same but use a different height is the volume of the sphere 2/3 the volume of the cylinder now explain your answer
Answers
From geometry, we know that:
• the volume of a sphere of radius r is:
\(V_S=\frac{4}{3}\cdot\pi\cdot r^3,\)• the volume of a cylinder of radius r and heigth h is:
\(V_C=h\cdot\pi\cdot r^2.\)If the volume of the sphere (Vs) is 2/3 the volume of the cylinder (Vc), we have:
\(\begin{gathered} V_S=\frac{2}{3}\cdot V_C, \\ \frac{4}{3}\cdot\pi\cdot r^3=\frac{2}{3}\cdot h\cdot\pi\cdot r^2. \end{gathered}\)Solving for h, we find that:
\(h=2r.\)We have found that the height of the cylinder is two times its radius.
Answer
• We have a sphere and cylinder with the same radius.
,• We know that the volume of the sphere is
\(V_S=\frac{2}{3}\cdot V_C.\)• By replacing the formulas of each volume, we find that the heigh of the cylinder is:
\(h=2r.\)pls guys help me pls :c

Answers
Answer: A. \(x\geq21\dfrac{2}{3}\) .
Step-by-step explanation:
The given inequation: \(81-1\dfrac{1}{5}x\leq55\)
\(\Rightarrow\ 81-\dfrac{6}{5}x\leq55\)
Multiplying 5 on both the sides, we get
\(5(81-\dfrac{6}{5}x)\leq5\times55\\\\\Rightarrow\ 405-6x\leq275\\\\\Rightarrow\ 6x\geq405-275\\\\\Rightarrow\ 6x\geq130\\\\\Rightarrow\ x\geq\dfrac{130}{6}\\\\\Rightarrow\ x\geq\dfrac{65}{3}\\\\\Rightarrow\ x\geq21\dfrac{2}{3}\)
Hence, the inequality for x is \(x\geq21\dfrac{2}{3}\) .
So, the correct option is A. \(x\geq21\dfrac{2}{3}\) ..
A coat check service charges $2 for the first hour and $1 for each additional hour or fraction of an hour. Which point is NOT included in the graph of the step function?
Answers
There is no point that is NOT included in the graph of the step function.
The coat check service charges $2 for the first hour and $1 for each additional hour or fraction of an hour.
To determine the point that is NOT included in the graph of the step function, we need to consider the charging scheme and analyze the pattern of charges.
The step function can be represented as follows:
For the first hour, the charge is a flat rate of $2.
For each additional hour or fraction of an hour, the charge is $1.
Let's analyze the points included in the graph:
(1, 2): This point represents the charge for the first hour, which is $2.
Now, let's consider the additional hours:
2. (2, 3): This point represents the charge for 2 hours, which is $2 for the first hour and $1 for the additional hour.
(3, 4): This point represents the charge for 3 hours, which is $2 for the first hour and $2 for the additional 2 hours.
(4, 5): This point represents the charge for 4 hours, which is $2 for the first hour and $3 for the additional 3 hours.
Based on the charging scheme, we can observe a pattern where the charge increases by $1 for each additional hour or fraction of an hour.
Since the charging scheme allows for any additional hour or fraction of an hour, there is no specific point that is excluded from the graph. Any positive value of x greater than or equal to 1 will have a corresponding point on the graph.
For similar question on service charges.
https://brainly.com/question/28093981
#SPJ8
3. The graph shows the Millennium Falcon traveling from Jakku to Takodan.
What is the average speed of the Millennium Falcon on this journey?

Answers
Evaluate each point using the velocity formula where d = distance, t = time, V = velocity
V = d/t
Now find the velocity at each point given.
So for the first point (omitting 0,0) we have:
V = 25,000/.25 = 100,000k/s
We have to switch the numbers up due to the fact that the axis are switch and for this to make sense we have to act like the time in seconds is the distance.
Now do this for every point and record them
1. 100,000
2. 66,667
3. 60,000
4. 66,667
5. 83,333
6. 100,000
7. 116,667
Now add all these numbers up and divide by the number of points
This gives you 84,762 k/s
What is the inverse of the function f(x) =x +3?
Answers
Answer:
f(x) = x + 3y = x + 3x = y - 3Inverse is h(x) = x - 3
Answer:
f^-1(x) = x - 3
.In a different biology lab, a population of single-cell parasites also reproduces hourly. An equation which gives the number of parasites, , after hours is Explain what the numbers 100 and 3 mean in this situation.
Answers
Answer: p=50 h=2
Step-by-step explanation:
so its 50 x 2=100 is the answer then u add 3
please help.
definitions: 1. definition of right triangle
2. definition of isosceles TrianglesReflexive
3. HL
4. definition of perpendicular
5. CPCTC
6. reflexive

Answers
From the two column proof below, we have seen ∠BAC ≅ ∠DAC by CPCTC
How to solve two column proof problems?The two column proof to show that ∠BAC ≅ ∠DAC is as follows:
Statement 1: ΔABD is Isosceles with base BD, AC ⊥ BD
Reason 1: Given
Statement 2: AB ≅ AD
Reason 2: Definition of isosceles Triangles
Statement 3: ∠1 and ∠2 are right angles
Reason 3: Definition of perpendicular
Statement 4: AC ≅ AC
Reason 4: Reflexive Property
Statement 5: ΔABC and ΔADC are right triangles
Reason 5: Definition of right triangle
Statement 6: ΔABC ≅ ΔADC
Reason 6: HL Congruency
Statement 7: ∠BAC ≅ ∠DAC
Reason 7: CPCTC
Read more about two column proof at; brainly.com/question/1788884
#SPJ1
Which of the following is not a true statement about the angles shown below? A H 3x x + 15 Z D x + 15 A. The measure of ZAHD is 30°. B. The measure of ZHDZ is 45°. C. The measure of ZHZD is 45°. D. The value of x is 30.
Answers
Answer:
A is not true
Step-by-step explanation:
Jasmine invests 2658 in a retirement account for with a fixed annual interest rate of 9% compounded continuously what will the account balayage be after 15 years
Answers
Answer:
$10,253.04
Step-by-step explanation:
suppose v varies directly as g, and v= 36 when g = 4. find v when g=11
Answers
Answer:
v = 99 when g = 11
Step-by-step explanation:
Set this up as an equation
36/4 = v/11
Cross multiply
36 × 11 = 4 × v
396 = 4v
Divide both sides by 4 to isolate variable v
396 ÷ 4 = 4v ÷ 4
99 = 1v
99 = v
In which month was the average number of hours worked by the website designers closest to 50 hours
- January
- February
- March
- April
Answers
The correct answer is March, as it was the month in which the average number of hours worked by the website designers was closest to 50 hours.
What is a month?A month is a unit of time typically consisting of 30 or 31 days. It is used for measuring periods of time, for example, when we say something happened "a month ago". Months are used in both the Gregorian calendar and the Julian calendar.
This data was gathered from a survey of website designers, which was conducted to determine the average number of hours each month that these professionals spent working.
In January, the average number of hours worked was 46.5. In February, it was 48.8. However, in March, the average number of hours worked was 49.4, which was the closest to 50 hours. This was followed by April, in which the average was 49.7.
Overall, it can be concluded that March was the month in which the average number of hours worked by website designers was closest to 50 hours. This is important data for website designers, as it allows them to understand the amount of time they should be spending on their work in order to be successful. It also helps employers gauge the workload of their website designers and ensure they are providing an adequate amount of work.
For more questions related to month
https://brainly.com/question/30403028
#SPJ1
Expand and simplify (2x - 1)(x + 3)(x - 5)
Answers
Answer:
2x^3-5x^2-28x+15 -------------------------expanded
2x^3-5x^2-28x+15--------------------simplified
Step-by-step explanation:
\left(2x-1\right)\left(x+3\right)\left(x-5\right)
=2x^2x+2x^2\left(-5\right)+5xx+5x\left(-5\right)-3x-3\left(-5\right)
simplyfied
\left(2x^2+5x-3\right)\left(x-5\right)
=2x^2x+2x^2\left(-5\right)+5xx+5x\left(-5\right)-3x-3\left(-5\right)
=2x^3-5x^2-28x+15
i want to most fat and juicy butt ever how do i get it ( i dont want to workout tho lolz)
Answers
Answer:
inject juice and put ramen
If you get this you are a critical thinker.
I enter the garden.
There are 34 people.
You kill 30.
How many people are in the garden.
Answers
Answer:
5
Step-by-step explanation:
If you killed 30 and there were 34 people there not including me then there would be 5 left.