At the middle school, 900 students ride the bus, and 300 students do not ride the bus. What percent of the students do not ride the bus?
Answers
Answer:
33.33 percent are not riding the bus
Step-by-step explanation:
Related Questions
Lengths of full-term babies in the US are Normally distributed with a mean length of 20.5 inches and a standard deviation of 0.90 inches. (Each question is worth 3 points) What percentage of full-term babies are between 19 and 21 inches long at birth
Answers
Answer:
66.48% of full-term babies are between 19 and 21 inches long at birth
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Mean length of 20.5 inches and a standard deviation of 0.90 inches.
This means that \(\mu = 20.5, \sigma = 0.9\)
What percentage of full-term babies are between 19 and 21 inches long at birth?
The proportion is the p-value of Z when X = 21 subtracted by the p-value of Z when X = 19. Then
X = 21
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{21 - 20.5}{0.9}\)
\(Z = 0.56\)
\(Z = 0.56\) has a p-value of 0.7123
X = 19
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{19 - 20.5}{0.9}\)
\(Z = -1.67\)
\(Z = -1.67\) has a p-value of 0.0475
0.7123 - 0.0475 = 0.6648
0.6648*100% = 66.48%
66.48% of full-term babies are between 19 and 21 inches long at birth
what are the real and complex solutions of x^3+2x^2+3x+6=0
Answers
These solutions can be further simplified, but they are all complex numbers. x = y - 2/3 = (8/9)√(5)/2 - 2/3
How to find?
To find the solutions of the cubic equation x²3 + 2x²2 + 3x + 6 = 0, we can use a combination of synthetic division and the quadratic formula.
First, we can use synthetic division to check if the equation has any rational roots. Since the coefficient of the highest degree term is 1, the possible rational roots are all factors of the constant term, 6. These are ±1, ±2, ±3, and ±6. We can use synthetic division to check if any of these values are roots of the equation:
-1 | 1 2 3 6
| -1 -1 -2
|-------------
| 1 1 2 4
-2 | 1 2 3 6
| -2 -2
|------------
| 1 0 1 4
-3 | 1 2 3 6
| -3 -3
|------------
| 1 -1 0 3
-6 | 1 2 3 6
| -6 24
|-------------
| 1 -4 27 0
None of the possible rational roots is a root of the equation. Therefore, the equation has no rational roots, and all the solutions are either irrational or complex.
Next, we can use the quadratic formula to find the solutions of the depressed cubic x²3 + 2x²2 + 3x + 6 = 0, which is obtained by substituting x = y - 2/3:
y²3 + py + q = 0
where p = 2 - (2/3)²2 = 4/9 and q = 6 - 4/3 = 16/3.
The quadratic formula gives:
c
y = [-p ± √(p²2 - 4q)]/2
Plugging in the values of p and q, we get:
y = [-4/9 ±√((4/9)²2 - 4(16/3))]/2
Simplifying:
c
y = [-4/9 ± √(16/81 - 64/9)]/2
c
y = [-4/9 ± √(-320/81)]/2
go
y = [-4/9 ± (8i/9)√(5)]/2
Therefore, the solutions of the cubic equation x²3 + 2x²2 + 3x + 6 = 0 are:
x = y - 2/3 = (-4/9 + (8i/9)√(5))/2 - 2/3
x = y - 2/3 = (-4/9 - (8i/9)√(5))/2 - 2/3
x = y - 2/3 = (8/9)√(5)/2 - 2/3
These solutions can be further simplified, but they are all complex numbers.
To know more about quadratic formula visit:
https://brainly.com/question/28001822
#SPJ1
2. Write the mixed number -5 4/9 as a fraction in three different ways
Answers
-5 4/9 is one way.
-5 = -45/9, so -45/9 + 4/9. -41/9 is another way.
-41/9 = -4.5555.... , so -4.5555... is another way.
-5 4/9 , -41/9 , -4.5555....The three ways of writing \(- 5\frac{4}{9}\) is - 49/9 and - 5.44.
What is a fraction?A fraction is written in the form of p/q, where q ≠ 0.
Fractions are of two types they are proper fractions in which the numerator is smaller than the denominator and improper fractions where the numerator is greater than the denominator.
Given, \(- 5\frac{4}{9}\).
One way of writing is - (45 + 4)/9 = - 49/9.
Another way of writing this is in a decimal form which is,
= - 5.44
learn more about fractions here :
https://brainly.com/question/10354322
#SPJ2
please help it’s due tomorrow
[x + y = -4
[x - y = 2
Answers
Answer:
which one substitution or elimination
Step-by-step explanation:
Substitution: (-1,-3 )
Elimination: (-1,-3)
i hope this helps you :)
Please mark me brainlest
I need to write 3 questions that you would ask to answer the problem.A steel beam can be cut to different lengths for a project. Assuming the weight of a steel beam is proportional to its length, what information would you need to know to write an equation that represents this relationship?
Answers
Two quantities x and y are proportional if they are related by:
\(y=a\cdot x\)Where a is known as the proportionality factor. In this case the quantities related are the length and the weight of a steal beam so the first two question would be:
- What's the length of the beam?
- What's its weight?
Then it is also important to know the proportionality factor so knowing that the length and the weight are proportionally related I would ask:
- What's the proportionality factor?
hay 1230 personas, entre hombres y mujeres. Si se sabe que el número de mujeres, supera en 150 al número de hombres. ¿Cuántos hombres están habitando la mini ciudad?
Answers
There are 540 men living in the mini city.
x + (x + 150) = 1230
Simplifying this equation, we get:
2x + 150 = 1230
Subtracting 150 from both sides, we get:
2x = 1080
Dividing both sides by 2, we get:
x = 540
Therefore, there are 540 men living in the mini city.
To check our answer, we can substitute x = 540 into our original equation:
540 + (540 + 150) = 1230
690 = 1230
This is false, so there must be an error in our calculation. We can double-check our work by trying a different approach.
We know that the number of women exceeds the number of men by 150, so we can represent the number of women as (x + 150). We also know that the total number of people is 1230, so we can set up an equation:
x + (x + 150) = 1230
Simplifying this equation, we get:
2x + 150 = 1230
Subtracting 150 from both sides, we get:
2x = 1080
Dividing both sides by 2, we get:
x = 540
For such more questions on mini
https://brainly.com/question/29266607
#SPJ8
pls help me solve this

Answers
The results of operations between vectors are, respectively:
Case A: u + w = <- 3, - 1>
Case B: - 6 · v = <6, 6>
Case C: 3 · v - 6 · w = <- 21, - 15>
Case D: 4 · w + 3 · v - 5 · u = <39, 4>
Case E: |w - v| = √(4² + 3²) = 5
How to determine the operations between vectors
In this problem we must determine the operations between vectors, this can be done by following definitions:
Vector addition
v + u = (x, y) + (x', y') = (x + x', y + y')
Scalar multiplication
α · v = α · (x, y) = (α · x, α · y)
Norm of a vector
|u| = √(x² + y²)
Now we proceed to determine the result of each operation:
Case A:
u + w = <- 6, - 3> + <3, 2>
u + w = <- 3, - 1>
Case B:
- 6 · v = - 6 · <- 1, - 1>
- 6 · v = <6, 6>
Case C:
3 · v - 6 · w = 3 · <- 1, - 1> - 6 · <3, 2>
3 · v - 6 · w = <- 3, - 3> + <- 18, - 12>
3 · v - 6 · w = <- 21, - 15>
Case D:
4 · w + 3 · v - 5 · u = 4 · <3, - 2> + 3 · <- 1, - 1> - 5 · <- 6, - 3>
4 · w + 3 · v - 5 · u = <12, - 8> + <- 3, - 3> + <30, 15>
4 · w + 3 · v - 5 · u = <39, 4>
Case E:
|w - v| = |<3, 2> - <- 1, - 1>|
|w - v| = |<4, 3>|
|w - v| = √(4² + 3²) = 5
To learn more on vectors: https://brainly.com/question/31900604
#SPJ1
Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
Need some help on this question please provide evidence on how you came up with the answer aswell.

Answers
Answer:
No and No
Step-by-step explanation:
Squaring a odd, whole, number results in a even number 99% of the time with the only exception being 1 (1^2 equals 1). If m is 3 and n is 5, mn would be 15, so if both m and n are odd they don't always equal a even number.
Answer:
Step-by-step explanation:
If we are dealing with whole real numbers.
Both answers are based on the same idea.
The product of two numbers is even only if at least one of the two multiplicands is even.
The square of an odd number can only result in an odd number. The reverse is true as well. The square root of an odd number can only be an odd number.
This comes from number theory where multiplication is the repeated addition of one number a certain number of times.
If the first number is even, then every time you add itself again results in an even number, It does not matter if you add an even or odd number of times.
If the first multiplicand is odd, the sum of two odd numbers is always even, adding a third odd multiplicand again results in an odd number, the fourth is even, the fifth is odd, the pattern continues forever. The summation of an even number of odd multiplicands results in an even number. The summation of an odd number of odd multiplicands results in an odd number.

Which ordered pair is in the solution set of the system of linear inequalities graphed below?
(0,2)
(2,4)
(-2,-4)
(-1,2)

Answers
Answer:
(0,2)
Step-by-step explanation:
PLZ HELP!! ITS ALMOST DUE!! ILL MARK BRAINLIEST!!

Answers
Answer: $32.74
Is your answer
Glad I could help!
Step-by-step explanation:
4. Explain the difference between (-5)2 and
- 5²
Answers
Answer:
The square of a negative number is a positive number as 2 negatives cancel when multiplied.
(-5)² = (-5)*(-5) = 25In this case the negative sign stays as is because it is not affected by a square.
- 5² = - (5)*(5) = -25What is the value of x?

Answers
Answer:
2x+2=58
2x=58-2=56
divide both sides by 2
x=28
The histogram shows the result of a survey about the number of hours students watch television on the weekend.
How many students participated in the survey?

Answers
The number of students who participated in the survey, based on the histogram showing the number of hours students watch television on the weekend, is 125.
What is a histogram?A histogram is a pictorial or graphical representation of categorical data, proportional to the frequency of a variable and whose width is equal to the class interval.
The number of students who watched between 0 - 4 hours = 20
The number of students who watched between 5 - 9 hours = 40
The number of students who watched between 10 - 14 hours = 30
The number of students who watched between 15 - 19 hours = 20
The number of students who watched between 20 - 24 hours = 15
The total number of students who participated = 125
Thus, using the histogram, the total number of students who participated in the survey was 125.
Learn more about histogram at https://brainly.com/question/17652335.
#SPJ1
Kaylib’s eye-level height is 48 ft above sea level, and Addison’s eye-level height is 85 and one-third ft above sea level. How much farther can Addison see to the horizon? Use the formula d = square root 3h/2, with d being the distance they can see in miles and h being their eye-level height in feet.
Answers
Answer is \(2\sqrt{2}\) mi
Given,
Kaylib’s eye-level height is 48 ft
Addison’s eye-level height is 85 and one-third ft above sea level.
From the formula d= \(\sqrt{3h/2}\),
get the difference as:
\(d=\sqrt{(3*(85+1/3))/2} - \sqrt{(3*48)/2}\)
=\(\sqrt{256/2} - \sqrt{3*24}\)
=\(\sqrt{128} - 6\sqrt{2}\)
=\(8\sqrt{2} - 6\sqrt{2}\)
d=\(2\sqrt{2}\)
Therefore, Addison sees \(2\sqrt{2}\)mi to the horizon
To know more about Height from sea level questions
https://brainly.com/question/10255119
NEED HELP ASAP 45 POINTS
What sequence of transformations when applied to triangle HIG, shows that triangle HIG is similar to triangle H’I’G
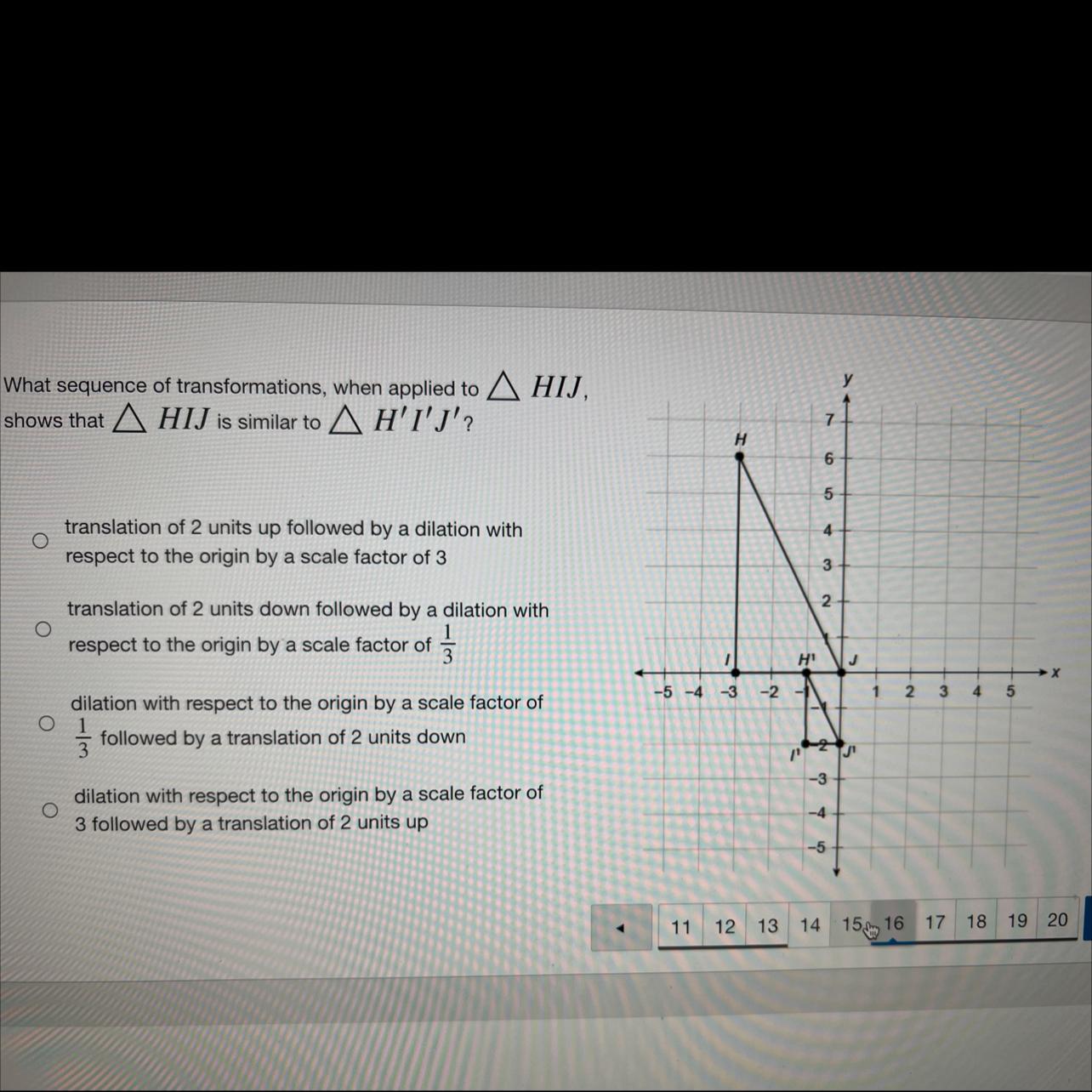
Answers
Answer:
dilation with respect to the origin by a scale factor of 1/3 followed by a translation of 2 units down
Step-by-step explanation:
The sides of the △ HIJ are:
IH = 6
IJ = 3
Applying the scale factor we obtain the sides of △ H'I'J '.
The scale factor is k = 1/3.
Therefore, we have:
I'H '= 2
I'J '= 1
Then, we move the △ H'I'J 2 units down.
A 42 gallon hot water tank hose 350 pounds of water what weight of water at 53 gallon tank hold
Answers
Answer:
441.66667 pounds
Step-by-step explanation:
divide 350/42 then multiply the quotient by 53
BRAINLIEST FOR ANSWER
A cylinder of water was holding a volume of 2 mL of water. An irregularly shaped stone was put into the cylinder and the volume rose to 8 mL. If the mass of the stone was 21 g, what was its density?
Answers
Answer:
3.5g/ml or 3.5g/cm³
Step-by-step explanation:
1cm³=1ML
Volume of the irregular shaped stone = New Volume of water in cylinder -initial Volume of water in cylinder
Volume of irregular shaped stone = 8ml-2ml
Volume of irregular shaped stone =6ml
Denisty =Mass/Volume
Density = 21g/6ml
Density = 3.5g/ml
Do Instagram have a where to see who screenshot your story?
Answers
The complement of an angle measures 41°. What is the measurement of the angle?
a.
49°
c.
139°
b.
82°
d.
98°
Answers
:)
Answer:
a. 49°
Step-by-step explanation:
x + 41 = 90
x = 90 - 41
x = 49°
Which is an equation of a direct proportion? y=8x y=
12x+4 y=12x y=4x−4
Answers
The equation of a direct proportion is A. y=8x.
What is a direct proportion?It should be noted that a direct proportion is also a direct variation. It is one when the relation between the two quantities have a value that's constant.
In this case, it's illustrated as y = 8x.
Let's say x = 1 y will be = (8 × 1) = 8
When x = 2, y = (8 × 2) = 16
In this case, it should be noted that the constant of 8 is illustrated.
In conclusion, the correct option is A.
Learn more about proportion on:
brainly.com/question/13742765
#SPJ1
Make A the subject..............................................

Answers
Answer:
Proofs attached to answer
Step-by-step explanation:
Proofs attached to answer
the equation a=0.003x^2+21.3 models the average ages of women when they first married since the year 1940. In this equation, a represents the average age and x represents the years since 1940. Estimate the year in which the average age of brides was the youngest
Answers
Answer:
Please help me important question in image
Step-by-step explanation:Please help me important question in image
Please help me important quePlease help me important question in image
stion in image
Please help me important question in image
Please help me important question in image
Answer:
The equation a=0.003x^2+21.3 models the average ages of women when they first married since the year 1940 in the United States. In this equation, a represents the average age and x represents the years since 1940. To estimate the year in which the average age of brides was the youngest, we need to find the minimum value of the quadratic function a=0.003x^2+21.3. This can be done by using the formula x=-b/2a, where b is the coefficient of x and a is the coefficient of x^2. In this case, b=0 and a=0.003, so x=-0/(2*0.003)=0. This means that the average age of brides was the lowest when x=0, which corresponds to the year 1940. The value of a when x=0 is a=0.003*0^2+21.3=21.3, so the average age of brides in 1940 was 21.3 years old. This is consistent with the historical data, which shows that the median age of women at their first wedding in 1940 was 21.5 years old. The average age of brides has been increasing since then, reaching 28.6 years old in 2021.
MARK AS BRAINLIEST!!!
what is1/3as a decimal
Answers
To find the decimal form of 1/3, we just divide 1 by 3 in the following way:
We can continue but the residue will always be 1, therefore, the decimal form of 1/3 is 0.3333....

In the month of March, the temperature at the South Pole varies over the day in a periodic way that can be modeled approximately by a trigonometric function.
The highest temperature is about -50°C, and it is
reached around 2 p.m. The lowest temperature is
about -54°C and it is reached half a day apart
from the highest temperature, at 2 a.m.
Find the formula of the trigonometric function that models the temperature T in the South Pole in March t hours after midnight. Define the function using radians.
Answers
The trigonometric function that models the temperature T in the South Pole in March t hours after midnight is given as follows:
T(t) = 2cos(π/12(t - 14)) - 52.
How to define the cosine function?The cosine function is defined as follows:
g(x) = acos(bx+c)+d.
The coefficients have these following roles:
a: amplitude.b: The period is of 2pi/B.c: phase shift.d: vertical shift.The lowest temperature is of -54ºC, while the highest is of -50ºC, with a difference of 4ºC, hence the amplitude is given as follows:
2a = 4
a = 2.
A function with amplitude of 2 would oscillate between -2 and 2, while this one oscillates between -54 and -50, hence the vertical shift is given as follows:
d = -50.
The period is of 24 hours, hence:
2π/B = 24
24B = 2π
B = π/12.
The highest value of the cosine function should be assumed at t = 0, but it is assumed at t = 14(2 p.m.), hence the phase shift is given as follows:
c = 14.
Thus the function is defined as follows:
T(t) = 2cos(π/12(t - 14)) - 52.
More can be learned about cosine functions at brainly.com/question/21558626
#SPJ1
The number of bacteria in a certain population increases according to a continuous exponential growth model, with a growth rate parameter of 5.8% per hour. How many hours does it take for the size of the sample to double?
Answers
It will take 5.189 hours to get doubled the size of Sample.
What is Exponential Function?A relation of the form y = \(a^x\), with the independent variable x ranging over the entire real number line as the exponent of a positive number a.
Given:
Growth rate = 5.8%
The continuous exponential growth model for populations is given by:
P(t)= \(P_0 e^{rt\)
So, r= 5.8%
r = 0.058
Now, the time taken to double the sample then P(t) = 2P(0).
So, P(t)= \(P_0 e^{0.058t\)
2P(0) = \(P_0 e^{0.058t\)
\(e^{0.058t\) = 2
Taking log on both side
log \(e^{0.058t\) = log 2
0.058 t = 0.301
t= 0.301/ 0.058
t = 5.189
Learn more about exponential Function here:
https://brainly.com/question/23064497
#SPJ1
evaluate 5214 ÷ 39
Answers
Answer: \(133\frac{9}{13}\) or \(\frac{1738}{13}\) or 133.7 (any three are correct)
Step-by-step explanation:
Hey there! I will give the following steps, if you have any questions feel free to ask me in the comments below.
Problem: Evaluate 5214 ÷ 39Step 1: 5214 / 39 = 133 with a remainder of 27.
133 with a remainder of 27
Because 39 is what we will be dividing it by, it will be our denominator.
Step 2: Express as a mixed fraction.
\(133\frac{27}{39}\)
Step 3: Simplify by dividing the denominator/numerator by 3.
\(133\frac{9}{13}\) or \(\frac{1738}{13}\) or 133.7
~I hope I helped you! :)~
What is the area of this quadrilateral?
4 cm
4 cm
1
3 cm

Answers
Answer:
14 square centimeters
Step-by-step explanation:
You gotta add the area of the first and second triangle.
First Triangle:
(1/2)x 4 x 4= 8cm
Second Triangle:
(1/2)x 4 x 3= 6cm
FINAL ANSWER: 6+8= 14cm
4 children each have some beads, the mean number of beads is 8 Rajiv brings some more beads. The mean number of 5 children is now 9 what is the numberx of beads Rajiv brings
Answers
Answer:
The number of beads Rajiv brings is: 13Step-by-step explanation:
Make a plan:In this question, we need to use the formula of means to solve the. We can set the number of beads Rajiv brings as X, and use the formula of mean to get the total number of beads that the Four(4) children have and the total number of beads that the Five(5) children have.
Solve the problem:Four(4) children each have some beads, the mean number of beads is: 8
We can get the total number of beads the Four(4) children have:4 * 8 = 32
Rajiv brings some more beads:We set the number of beads Rajiv brings as:
x, so the total number of beads that the Five(5) children have is:
32 + x
The mean number of the Five(5) children is now: 9
We can get the total number of beads that the Five(5) children have:5 * 9 = 45
Now, we have the equation:32 + x = 45
x + 32 = 45
- 32 = -32
x = 13
By solving the above equation, you can get:
x = 13
Hence, The number of beads Rajiv brings is:13
Hope this helps!
Find all solutions of each equation on the interval 0≤ x <2pie
tan² x sec² x +2 sec²x - tan²x =2
Answers
The trigonometric equations has the following solutions: x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.
How to solve a trigonometric equation
In this problem we find the case of a trigonometric equation, whose solutions on the interval [0, 2π] must be found. This can be done by both algebra properties and trigonometric formulae. First, write the entire expression:
tan² x · sec² x + 2 · sec² x - tan² x = 2
Second, use trigonometric formulas to reduce the number of trigonometric functions:
tan² x · (tan² x + 1) + 2 · (tan² x + 1) - tan² x = 2
Third, expand the equation:
tan⁴ x + tan² x + 2 · tan² x + 2 - tan² x = 2
tan⁴ x + 2 · tan² x = 0
Fourth, factor the expression:
tan² x · (tan² x - 2) = 0
tan² x = 0 or tan² x = 2
tan x = 0 or tan x = ± √2
Fifth, determine the solutions to trigonometric equation:
x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.
To learn more on trigonometric equations: https://brainly.com/question/22624805
#SPJ1