An involutory function is a function that is its own inverse. Let f:] - b , infinty [-->] 0, infinity[ and f(x) = 2/x+b Which among the following statements is true? a. f is an involutory function if and only if b=2 b. f is an involutory function if and only if b=0
c. f is an involutory function if and only if b>-1 d. None of the mentioned
Answers
The true statement is C. f is an involutory function if and only if b>-1
What is an involutory function?An involutory function is simply described as a function that is seen as the inverse function of itself
From the information given, we have the function as;
f(x) = 2 / x+b
Find the values of b, we have;
f (f(x)) = f (2/x+b)
Take the inverse
f(f(x) = 2/(2/x+b)+b
Factorize the expression, we have;
f(f(x)) = 2× (1/(1/x+b/2))+b
Then, we get;
f(f(x)) = x and 1/(1/x+b/2) = x.
Equate the expressions;
1/(1/x+b/2) = x
1/x+b/2 = x²
collect the terms, we have;
b/2 = x²-1/x
b = 2x² -1
Then, we have that function would be positive for values of x > 0.
b> -1
Learn more about function at: https://brainly.com/question/3831584
#SPJ4
Related Questions
Solve the equation C^2 =4
Answers
Answer:
2
Step-by-step explanation:
Hey there!
The equation is asking us, c x c = 4
What is c?
Well the only number that is equal to 4 when you square it is 2
The two whole numbers that the square root of 11 is inbetween are _______
and ________
Answers
Answer:
3 and 4
Explanation:
The two perfect squares closest to √11 are √9 and √16, which are 3 and 4, respectively.
Hope this helps!
Show that the three medians of each triangle in problem 5 intersect in a common point. (center of gravity)
Answers
We will solve as follows:
We have the triangles:
*
We can determine its medians by calculating the mid-points of each side, and then plot t


Given the following two sets of data. Illustrate the Merge algorithm to merge the data. Compute the runtime as well.
A = 23, 40, 67, 69
B = 18, 30, 55, 76
Show the complete work.
Answers
Given the following two sets of data. Illustrate the Merge algorithm to merge the data. Compute the runtime as well.
A = 23, 40, 67, 69
B = 18, 30, 55, 76
The algorithm that merges the data sets is known as Merge Algorithm. The following are the steps involved in the Merge algorithm.
Merge Algorithm:
The given algorithm is implemented in the following way:
Algorithm Merge (A[0..n-1], B[0..m-1], C[0..n+m-1]) i:= 0 j:= 0 k:= 0.
while i am < n and j < m do if A[i] ≤ B[j] C[k]:= A[i] i:= i+1 else C[k]:= B[j] j:= j+1 k:= k+1 end while if i = n then for p = j to m-1 do C[k]:= B[p] k:= k+1 end for else for p = I to n-1 do C[k]:= A[p] k:= k+1 end for end if end function two lists, A and B are already sorted and are to be merged.
The third list, C is an empty list that will hold the final sorted list.
The runtime of the Merge algorithm:
The merge algorithm is used to sort a list or merge two sorted lists.
The runtime of the Merge algorithm is O(n log n), where n is the length of the list. Here, we are merging two lists of length 4. Therefore, the runtime of the Merge algorithm for merging these two lists is O(8 log 8) which simplifies to O(24). This can be further simplified to O(n log n).
Now, we can compute the merge of the two lists A and B to produce a new sorted list, C. This is illustrated below.
Step 1: Set i, j, and k to 0
Step 2: Compare A[0] with B[0]
Step 3: Add the smaller value to C and increase the corresponding index. In this case, C[0] = 18, so k = 1, and j = 1
Step 4: Compare A[0] with B[1]. Add the smaller value to C. In this case, C[1] = 23, so k = 2, and i = 1
Step 5: Compare A[1] with B[1]. Add the smaller value to C. In this case, C[2] = 30, so k = 3, and j = 2
Step 6: Compare A[1] with B[2]. Add the smaller value to C. In this case, C[3] = 40, so k = 4, and i = 2
Step 7: Compare A[2] with B[2]. Add the smaller value to C. In this case, C[4] = 55, so k = 5, and j = 3
Step 8: Compare A[2] with B[3]. Add the smaller value to C. In this case, C[5] = 67, so k = 6, and i = 3
Step 9: Compare A[3] with B[3]. Add the smaller value to C. In this case, C[6] = 69, so k = 7, and j = 4
Step 10: Add the remaining elements of A to C. In this case, C[7] = 76, so k = 8.
Step 11: C = 18, 23, 30, 40, 55, 67, 69, 76.
The new list C is sorted. The runtime of the Merge algorithm for merging two lists of length 4 is O(n log n). The steps involved in the Merge algorithm are illustrated above. The resulting list, C, is a sorted list that contains all the elements from lists A and B.
Learn more about Merge Algorithm: https://brainly.com/question/30899498
#SPJ11
What is an equation of the line that passes through the point ( − 1 , − 3 ) and is perpendicular to the line x − 2 y = 14? pls answer will mark you as brainiest
Answers
Answer:
y = -2x - 5
Step-by-step explanation:
First rewrite the second equation into y = mx + b format:
x - 2y = 14
2y = x - 14
y = x/2 - 14/2 (Divide both sides by 2)
y = 1/2x - 7
A line perpendicular to another has the negative reciprocal slope
So the slope of our first equation is -2. (Flip 1/2 = 2, then take the opposite)
Plug in the points (-1, -3) for the x and y coordinates.
x (x coordinate) = -1
y (y coordinate) = -3
slope (m) = -2
-3 = -1(-2) + b
-3 = 2 + b
-3 - 2 = b
b = -5
The equation of the line is y = -2x - 5. Hope this helps! :)
Answer:
y = -2x - 5 or 2x + y = -5
Step-by-step explanation:
Let's find the slope of the given line.
-2y = -x + 14
y = 1/2(x) -7
m = 1/2
The slope of a line perpendicular is the negative reciprocal of 1/2, which is -2
Now use the point-slope form of a line
y + 3 = -2(x + 1)
y + 3 = -2x - 2
y = -2x - 5 or 2x + y = -5
Raul and Bobby are brothers who are saving to buy a new video game console. Bobby contributed $25 and plans to save $10 per week. Raul contributed $20 and plans to save $15 per week. What expression represents the total amount Bobby and Raul will have in w weeks
Answers
Answer:
25+20+(10w+15w)
Step-by-step explanation:
in the parenthisis is what they get each week
so each week its starts with 45 plus what ever they get each week and what ever they get times w for each week so if they do it for 5 weeks its
25+20+[(10x5)+(15x5)]
45+(50+75)= 170
Simplify.
(4.173 – 1.32)+(-7.6x + 3.54)
0 -3.43x + 2.22
O 2.85x – 4.06
O 7.712 – 8.92
0 11.77x + 4.86
Answers
Answer
your answer is not shown but the correct answer based on the top is going to be −
7.6x + 6.393
please check to ensure that you wrote the problem correctly as well as your answers.
Step-by-step explanation:
The amount a babysitter charges for babysitting services per hour is shown in the table below. What is the rate of change and what does it represent? What is the y Intercept and what does it represent?

Answers
Answer:
y=8x+2
Step-by-step explanation:
the slope is 8 and the y intercept is 2
the slope is 8 dollars the increase of the price per hour. the yintercept is the amount she get for 0 hours (2 dollars)
1,10
2,18
8/1 is 8
10=8*1+b
10=8+b
2=b
the value of result in the following expression will be 0 if x has the value of 12. result = x > 100 ? 0 : 1;
Answers
The value of result in the following expression will be 0 if x has the value of 12:
result = x > 100 ? 0 : 1.
The expression given is known as a ternary operator.
It's a short form of if-else.
The ternary operator is written with three arguments separated by a question mark and a colon:
`variable = (condition) ? value_if_true : value_if_false`.
Here, `result = x > 100 ? 0 : 1;` is a ternary operator, and its meaning is the same as below if-else block.if (x > 100) { result = 0; } else { result = 1; }
As per the question, we know that if the value of `x` is `12`, then the value of `result` will be `0`.
Hence, the answer is `0`.
Learn more about value from the given link;
https://brainly.com/question/54952879
#SPJ11
Find the areas of the shaded sections.

Answers
Question
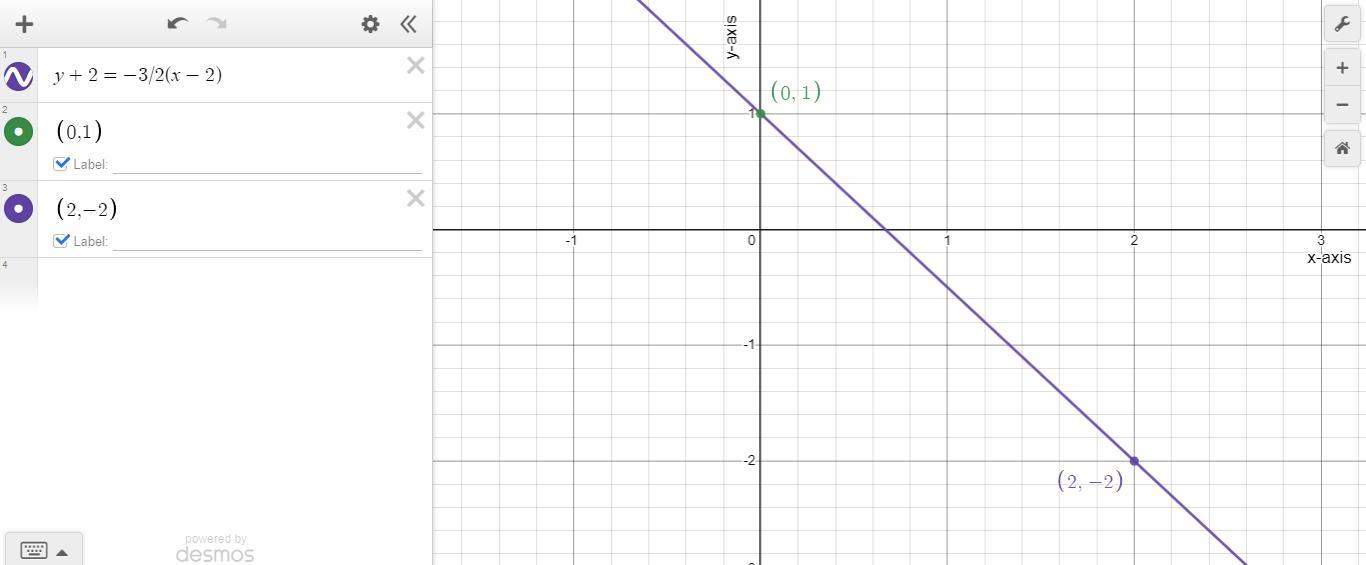
What equation is graphed in this figure?
Responses
y−4=−23(x+2)
y minus 4 equals negative fraction 2 over 3 end fraction left parenthesis x plus 2 right parenthesis
y+2=−32(x−2)
y plus 4 equals negative fraction 3 over 2 end fraction left parenthesis x minus 2 right parenthesis
y−3=32(x+1)
y minus 3 equals fraction 3 over 2 end fraction left parenthesis x plus 1 right parenthesis
y+1=−23(x−3)
y plus 1 equals negative fraction 2 over 3 end fraction left parenthesis x minus 3 right parenthesis
Number graph that ranges from negative five to five on the x and y axes. A line passes through begin ordered point zero comma one end ordered pair and begin ordered pair two comma negative two end ordered pair
Answers
The equation which is graphed in this figure (see attachment) is: C. y + 2 = −3/2(x − 2)
"y plus 4 equals negative fraction 3 over 2 end fraction left parenthesis x minus 2 right parenthesis."
How to determine the number of solutions?Mathematically, the point-slope form of a straight line can be calculated by using this mathematical expression:
y - y₁ = m(x - x₁) or y - y₁ = (y₂ - y₁)/(x₂ - x₁)(x - x₁)
Where:
m represents the slope.x and y represents the data points.From the information provided about this graph, we have the following data points on its line:
Points on the x-axis = (0, 2).
Points on the y-axis = (1, -2).
At data point (0, 3), a linear equation of the first line can be calculated in slope-intercept form as follows:
y - y₁ = (y₂ - y₁)/(x₂ - x₁)(x - x₁)
y - (-2) = (-2 - 1)/(2 - 0)(x - 2)
y + 2 = -3/2(x - 2)
Read more on slope here: https://brainly.com/question/11586413
#SPJ1
Uh help me I guess you don’t have to if you don’t want to though

Answers
Answer:
12cm³
Step-by-step explanation:
1/2x2x6x2=12cm³
Answer:
6x2 well the answer is 24 so like
Step-by-step explanation:
armer abe has a budget of $300 to build a rectangular pen to protect his rambunctious sheep. he decides that three sides of the pen will be constructed with chain-link fence, which costs only $1 per foot. farmer abe decides that the fourth side of the pen will be made with sturdier fence, which costs $5 per foot. find the dimensions of the largest area the pen can enclose.
Answers
Let x be the length of the pen and y be the width of the pen.
The total cost of the pen is given by:
Cost = 3x + 5y = 300
3x + 5y = 300
3x = 300 - 5y
x = (300 - 5y)/3
The area of the pen is given by:
Area = xy = (300 - 5y)/3 * y
I will rate as soon as I can, thank you.
a) Show | > is normalized
b) Show it's an eigenvector of the lowering operator c) how is it a eigenvector of ^t ?
d) what is its eigenvalue
∣α⟩=e−21∣α∣2∑n=0[infinity]n!αn∣n⟩
Answers
a) |α⟩ is normalized if α = |α|² and α is a positive real number.
b) |α⟩ is an eigenvector of the lowering operator with eigenvalue λ = |α|.
c) |α⟩ is also an eigenvector of the transpose operator t with eigenvalue μ = |α|.
d) The eigenvalue of |α⟩ with respect to t is μ = |α|.
a) To show that |α⟩ is normalized, we need to compute its norm, which is given by ⟨α|α⟩. Let's calculate it:
⟨α|α⟩ = e(-|α|²) ∑n=0 [infinity] (n!/\(\alpha^n\) ∑m=0 [infinity] (m!/\(\alpha^m\)) ⟨n|m⟩
Since the states |n⟩ form an orthonormal basis, ⟨n|m⟩ = δ_n,m (Kronecker delta), which equals 1 when n = m and 0 otherwise. Therefore, the sum simplifies to:
⟨α|α⟩ = e(-|α|²) ∑n=0 [oo] (n!/αⁿ)
Using the identity eˣ = ∑k=0 [infinity] (\(x^k\) / k!), we can rewrite the sum as:
⟨α|α⟩ = e(-|α|²) \(e^\alpha\) = e(α - |α|²)
Now, to show that |α⟩ is normalized, we need to confirm that ⟨α|α⟩ = 1:
e(α - |α|²) = 1
This equation holds true when α - |α|² = 0, which implies that α = |α|². Since α is a complex number, we can write it as α = |α|e(iθ). Substituting this into the equation, we get:
|α|e(iθ) = |α|²
Dividing both sides by |α|, we obtain:
e(iθ) = |α|
This equation is satisfied when θ = 0, which means α is a positive real number. Therefore, |α⟩ is normalized.
b) To show that |α⟩ is an eigenvector of the lowering operator, we need to demonstrate that a|α⟩ = λ|α⟩, where a is the lowering operator. The lowering operator is defined as a = ∑n=0 [oo] √(n+1) |n⟩⟨n+1|.
Let's compute a|α⟩:
a|α⟩ = ∑n=0 [oo] √(n+1) |n⟩⟨n+1| (\(e^{-1/2}\)|α|²/2 ∑m=0 [infinity] (m!/α) |m⟩)
We can interchange the order of the sums and use the property of the Kronecker delta to simplify the expression:
a|α⟩ = ∑n=0 [oo] √(n+1) (e(-1/2)|α|²/2 (n+1)!/αⁿ⁺¹) |n⟩
Next, we can factor out the common terms:
a|α⟩ = (\(e^{-1/2}\)|α|²/2) ∑n=0 [oo] √(n+1) (n+1)!/αⁿ⁺¹ |n⟩
Now, notice that the term in the sum is precisely the coefficient of αⁿ in the series expansion of eᵃ. Therefore, we can rewrite the expression as:
a|α⟩ = (\(e^{-1/2}\)|α|²/2) eᵃ |α⟩
Since |α⟩ is defined as \(e^{-1/2}\)|α|²/2 ∑n=0 [oo] (n!/αⁿ) |n⟩, we can simplify further:
a|α⟩ = |α| |α⟩
Therefore, we have shown that |α⟩ is an eigenvector of the lowering operator with eigenvalue λ = |α|.
c) To show that |α⟩ is an eigenvector of the t operator, we need to demonstrate that t |α⟩ = μ |α⟩, where t is the transpose operator.
The transpose operator acts on the ket vectors by taking the complex conjugate of their components. Therefore, we have:
t |α⟩ = (t \(e^{-1/2}\)|α|²/2) ∑n=0 [oo] (n!/αⁿ) (t |n⟩)
Since the transpose of |n⟩ is its bra vector, we can write:
t |α⟩ = (t \(e^{-1/2}\)|α|²/2) ∑n=0 [oo] (n!/αⁿ) ⟨n|
Now, using the definition of the transpose of a complex number, we have:
t |α⟩ = (\(e^{-1/2}\))|α|²/2) ∑n=0 [oo] (n!/αⁿ) ⟨n|
Finally, notice that the expression inside the sum is the same as the coefficient of αⁿ in the series expansion of eᵃ. Therefore, we can simplify further:
t |α⟩ = (\(e^{-1/2}\)|α|²/2) eᵃ ∑n=0 [oo] (n!/αⁿ) ⟨n|
Since |α⟩ is defined as \(e^{-1/2}\)|α|²/2 ∑n=0 [oo] (n!/αⁿ) |n⟩, we can rewrite the expression as:
t |α⟩ = |α| |α⟩
Therefore, |α⟩ is an eigenvector of the t operator with eigenvalue μ = |α|.
d) The eigenvalue of |α⟩ with respect to the t operator is μ = |α|.
To know more about real number:
https://brainly.com/question/17019115
#SPJ4
Wildlife: Mallard Ducks and Canada Geese For mallard ducks and Canada geese, what percentage of nests are successful (at least one offspring survives)? Studies in Montana, Illinois, Wyoming, Utah, and California gave the following percentages of successful nests (Reference: The Wildlife Society Press, Washington, D.C.). x: Percentage success for mallard duck nests 56 85 52 13 39 y: Percentage success for Canada goose nests 24 53 60 69 18 (a) Use a calculator to verify that ??-245: ??2 = 14,755, 2y = 224; and (b) Use the results of part (a) to compute the sample mean, variance, and (c) Use the results of part (a) to compute the sample mean, variance, and ??? = 12,070. standard deviation for x, the percent of successful mallard nests. standard deviation for y, the percent of successful Canada goose nests.
Answers
(a) Using the given data, we can verify the calculations as follows: ∑x = 245, ∑x^2 = 14,755, ∑y = 224.
(b) To compute the sample mean, variance, and standard deviation for the percentage success of mallard duck nests (x), we use the formulas:
Sample Mean (x) = ∑x / n
Variance (s^2) = (∑x^2 - (n * x^2)) / (n - 1)
Standard Deviation (s) = √(s^2)
(c) Applying the formulas, we can compute the sample mean, variance, and standard deviation for x as follows:
Sample Mean (x) = 245 / 5 = 49
Variance (s^2) = (14,755 - (5 * 49^2)) / (5 - 1) = 4,285
Standard Deviation (s) = √(4,285) ≈ 65.5
Similarly, for the percentage success of Canada goose nests (y), the calculations can be done using the same formulas and the given values from part (a).
Learn more about standard deviation here: brainly.com/question/29808998
#SPJ11
Lyla i am not cheating they are practice questions stop deleting my question Guys i need help
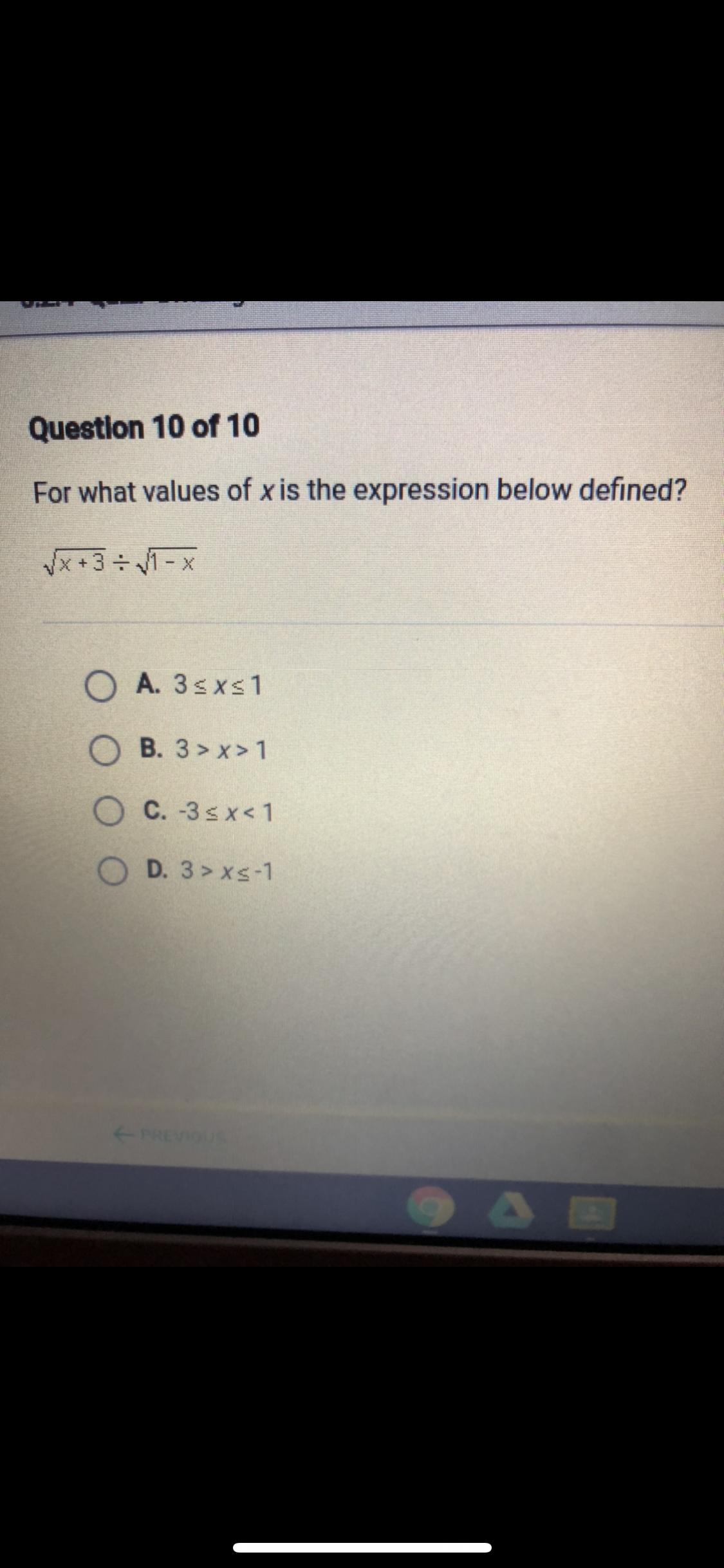
Answers
Answer:
C
Step-by-step explanation:
If you simplify the equation you get \(\sqrt{\frac{x+3}{1-x} }\). To solve a square root function, you need to set up\(\sqrt{\frac{x+3}{1-x} }\geq 0\). You can take the square root of both sides to get \(\frac{x+3}{1-x} \geq 0\). Then, we identify the intervals that will satisfy the equation, which is -3 ≤ x < 1.
Sorry if the explanation is kind of confusing, I wasn't sure how to describe it.
Answer:
the answer is c
Step-by-step explanation:
hope this helps!
~mina
The circumference of a circle of diameter 10 cm is _____.
A
3.14 cm
B
0.314 cm
C
314 cm
D
31.4 cm
Answers
For a circle with a diameter of 10 cm, the circumference would be C = π(10) = 31.4 cm. The correct option is (D) 31.4 cm.
The circumference of a circle can be calculated using the formula C = πd, where C represents the circumference and d represents the diameter of the circle.
We have the diameter of the circle is 10 cm, we can substitute this value into the formula:
C = π * 10 cm
Calculating the circumference using an approximate value of π as 3.14:
C ≈ 3.14 * 10 cm
C ≈ 31.4 cm
Therefore, the circumference of a circle with a diameter of 10 cm is approximately 31.4 cm.
The correct answer is D) 31.4 cm.
To know more about circumference refer here :
https://brainly.com/question/28757341#
#SPJ11
what is the slope and point of y-1=-4(x+3)

Answers
Answer:
M= -4
Point (3,1)
Step-by-step explanation:
The slope is -4
the point is (3,1)
suppose that mean retail price per gallon of regular grade gasoline 3.43 is with a standard deviation of and that the retail price per gallon has a bell-shaped distribution. note: please use empirical rule approximations for this problem. a. what percentage of regular grade gasoline sells for between and per gallon (to decimal)? b. what percentage of regular grade gasoline sells for between and per gallon (to decimal)? c. what percentage of regular grade gasoline sells for less than per gallon (to decimal)?
Answers
The 95% of regular grade gasoline sells for between $3.23 & $3.63 and per gallon (to decimal) and 85% of regular grade gasoline sells for between $3.23 & $3.53 and per gallon (to decimal) and 16% percentage of regular grade gasoline sells for less than $3.53 per gallon (to decimal).
Suppose that mean retail price per gallon of regular grade gasoline 3.43.
empirical rule explains that approximately 68%,95% and 99.7% of data lies between (µ ± 1*σ) ,(µ ± 2*σ) and (µ ± 3*σ) respectively.
⇒If some data {x} are normally distributed, the corresponding {z} will be normal with mean 0 and standard deviation 1 where the correspondence between the {x} and {z} is given by
z = \(\frac{x-\mu}{\sigma}\)Such z's are called z-scores.
(µ ± 1*σ)=68%
(µ ± 2*σ)=95%
(µ ± 3*σ)=99.7%
a)
P(3.23<x<3.63) =\(P[ \frac{(x1- \mu)}{\sigma} < z < \frac{(x2- \mu)}{\sigma}} ]\)
=P[( \(\frac{3.23-3.43}{0.10}\) < z < \(\frac{3.63-3.43}{0.10}\) ]
=P[-2 < z < 2 ]
=0.95
=95.0 %
b)
P(3.23<x<3.53) =\(P[ \frac{(x1- \mu)}{\sigma} < z < \frac{(x2- \mu)}{\sigma}} ]\)
=P[( \(\frac{3.23-3.43}{0.10}\) < z < (\(\frac{3.53-3.43}{0.10}\) ]
=P[-2 < z < 1 ]
=0.815
=81.5 %
c)
P(x>3.53) =\(P[ z > \frac{x-\mu}{\sigma} ]\)
=P[ z > \(\frac{3.53-3.43}{0.10}\) ]
=P[ z > 1 ]
=0.16
=16.0 %.
Therefore, 95% of regular grade gasoline sells for between $3.23 & $3.63 and per gallon (to decimal) and 85% of regular grade gasoline sells for between $3.23 & $3.53 and per gallon (to decimal) and 16% percentage of regular grade gasoline sells for less than $3.53 per gallon (to decimal).
For more such questions on normal distribution
https://brainly.com/question/14916937
#SPJ4
If the hcf of 65 and 117 is expressible in the form of 65 m-117,the the value of m is
Answers
If the HCF of 65 and 117 is expressible in the form of 65 m-117, then the value of m is 2.
To find the value of m, follow these steps:
Since the HCF (65, 117) = 13 and the HCF (65, 117) = 65m - 117, then we can say that 65m - 117= 13.Solving the equation, we get 65m= 130 ⇒m= 130/65= 2.Therefore, the value of m is 2.
Learn more about HCF:
https://brainly.com/question/21504246
#SPJ11
a normal distribution is observed from the times to complete an obstacle course. the mean is 69 seconds and the standard deviation is 6 seconds. using the empirical rule, what is the probability that a randomly selected finishing time is greater than 87 seconds? provide the final answer as a percent rounded to two decimal places. provide your answer below: $$ %
Answers
The probability that a randomly selected finishing time is greater than 87 seconds is 14.08%. This can be calculated using the empirical rule.
The empirical rule states that for any data that is normally distributed, about 68% of the data will fall within one standard deviation of the mean (in this case, within 69 ± 6 seconds). Approximately 95% of the data will fall within two standard deviations (in this case, within 69 ± 12 seconds), and about 99.7% of the data will fall within three standard deviations (in this case, within 69 ± 18 seconds).Given the mean and standard deviation given, we can calculate the probability that a randomly selected finishing time is greater than 87 seconds.
We can do this by subtracting the area under the curve from the mean to the value we are interested in (in this case, 87 seconds). Since the total area under the curve is 1, subtracting the area from the mean to 87 seconds will give us the desired probability.To calculate the area under the curve, we need to calculate the Z-score, which is the number of standard deviations away from the mean a particular value is. In this case, the Z-score is (87 - 69) / 6, which is 2.16. Using a Z-table, the probability of a Z-score of 2.16 or higher is 0.8592. Therefore, the probability that a randomly selected finishing time is greater than 87 seconds is 1 - 0.8592, which is 0.1408. Rounding to two decimal places, this is 14.08%.
Read more about probability at
https://brainly.com/question/29351756
#SPJ11
5 1/4 minus 2 5/8 in fraction form HELP!
Answers
Answer: 2.625
Explanation: 5 1/4 - 2 5/8 = 21/8 = 2 5/8 = 2.625
Answer:
I think the awnser to this is 2 5/8
The sum of four consecutive integers is 222. Find the integers
Answers
==============================================
Work Shown:
x = first integerx+1 = second integerx+2 = third integerx+3 = fourth integerSum the integers to get 222
(first)+(second)+(third)+(fourth) = 222
(x)+(x+1)+(x+2)+(x+3) = 222
4x+6 = 222
4x = 222-6
4x = 216
x = 216/4
x = 54 is the first integer
x+1 = 54+1 = 55 is the second integer
x+2 = 54+2 = 56 is the third integer
x+3 = 54+3 = 57 is the fourth integer
The sequence is 54, 55, 56, 57
Check:
54+55+56+57 = 222
An Olympic swimming pool is 25 meters long. How long is the pool in yards?
Answers
1. #40 pg 325 in book (section 7.3) Determine if the following statements are true or false, and justify your answer. (a) If V is a finite dimensional vector space, then V cannot contain an infinite linearly independent subset. (b) If Vi and V2 are vector spaces and dim(V1) < dim (V2), then V1 ⊂ V2. 2. #50 pg 198 in book (section 4.3) Determine if the following statements are true or false, and justify your answer. (a) If xo is a solution to Ax=b, then xo is in row(A). (b) If A is a 4x13 matrix, then the nullity of A could be equal to 5.
Answers
a) If V is a finite-dimensional vector space, then V cannot contain an infinite linearly independent subset. This statement is false.
(b) If Vi and V2 are vector spaces and dim(V1) < dim (V2), then V1 ⊂ V2. This statement is false.
(a) If xo is a solution to Ax=b, then xo is in row(A). This statement is false.
(b) If A is a 4x13 matrix, then the nullity of A could be equal to 5. This statement is false.
(a) False. A vector space can have an infinite linearly independent subset, but only if it is infinite-dimensional. For example, the vector space of polynomials has an infinite linearly independent subset {1, x, \(x^2\), \(x^3\), ...}.
(b) False. Just because the dimension of V1 is less than V2 does not necessarily mean V1 is a subset of V2. For example, V1 could be the x-axis in \(R^2\) and V2 could be the entire plane.
(a) False. Just because xo is a solution to Ax=b does not mean xo is in row(A). xo could be any vector that satisfies the equation Ax=b.
(b) False. The nullity of matrix A is equal to the dimension of its null space. The null space is the set of all solutions to the homogeneous equation Ax=0. Since A has 13 columns, the maximum rank it can have is 13. Therefore, the nullity of A can be at most 13-4=9. It cannot be equal to 5.
To learn more about the subset, refer:-
https://brainly.com/question/24138395
#SPJ11
If n=28, x
ˉ
(x−bar)=30, and s=16, construct a confidence interval at a 90% confidence level. Assume the data came from a normally distributed population. Give your answers to one decimal place. <μ< Question 5 If n=520 and p ′
(p-prime) =0.83, construct a 90% confidence interval. Give your answers to three decimals. 巨0/1pt 510⇄3 (i) Details
(p-hat) in place of p :
. Question Help: □ yidee Question 6 Out of 100 people sampled, 57 had kids. Based on this, construct a 9996 ec true population proportion of people with kids. true popuiation proportion of people with kids. Give your answers as decimals, to three places
Answers
The confidence interval for the population mean with a 90% confidence level is (24.7, 35.3). The confidence interval for the population proportion with a 90% confidence level is (0.785, 0.935).
To construct a confidence interval for the population mean, we use the formula: x ± z * (s/√n), where x is the sample mean, s is the sample standard deviation, n is the sample size, and z is the critical value corresponding to the desired confidence level. In this case, with n = 28, x = 30, s = 16, and a 90% confidence level, the critical value is approximately 1.645. Plugging in these values, we get the confidence interval (24.7, 35.3).
To construct a confidence interval for the population proportion, we use the formula: p ± z * √(p(1-p)/n), where p is the sample proportion and z is the critical value. In this case, with n = 520 and p = 0.83, and a 90% confidence level, the critical value is approximately 1.645. Plugging in these values, we get the confidence interval (0.785, 0.935).
For the third question, the sample proportion is 57/100 = 0.57. Since the sample size is large (n > 30), we can use the normal distribution to construct a confidence interval. The margin of error is approximately 1.96 * √((0.57 * 0.43) / 100) ≈ 0.088. Therefore, the confidence interval is (0.482, 0.658), indicating that we are 99% confident that the true population proportion of people with kids falls within this range.
To learn more about standard deviation click here
brainly.com/question/29115611
#SPJ11
In ΔEFG, g = 34 inches, e = 72 inches and ∠F=21°. Find the area of ΔEFG, to the nearest square inch.
Answers
The area of triangle EFG, to the nearest square inch, is approximately 1061 square inches.
To find the area of triangle EFG, we can use the formula:
\(Area = (1/2) \times base \times height\)
In this case, the base of the triangle is FG, and the height is the perpendicular distance from vertex E to side FG.
First, let's find the length of FG. We can use the law of cosines:
FG² = EF² + EG² - 2 * EF * EG * cos(∠F)
EF = 72 inches
EG = 34 inches
∠F = 21°
Plugging these values into the equation:
FG² = 72² + 34² - 2 * 72 * 34 * cos(21°)
Solving for FG, we get:
FG ≈ 83.02 inches
Next, we need to find the height. We can use the formula:
height = \(EF \times sin( \angle F)\)
Plugging in the values:
height = 72 * sin(21°)
height ≈ 25.52 inches
Now we can calculate the area:
\(Area = (1/2) \times FG \times height\\Area = (1/2)\times 83.02 \times 25.52\)
Area ≈ 1060.78 square inches
For more such questions on triangle
https://brainly.com/question/1058720
#SPJ8
Please help me with my math question!!

Answers
so basically, just write an equation w -3/4 as the rate of change. For example: y= -3/4x + 4
(c) immediately after the switch is open (after being closed a long time)... ...the current through the inductor is = 20.4 correct: your answer is correct. ma ...the current through r2
Answers
The current through R2 will depend on the values of the components in the circuit and the initial current through the inductor. Without more information, it is not possible to determine the current through R2.
After the switch is open, the current through the inductor will continue to flow in the same direction but will gradually decrease over time. The current through R2 will depend on the values of the components in the circuit and the initial current through the inductor. Without more information, it is not possible to determine the current through R2.
We want to know the current through resistor R2 immediately after the switch is opened, given that the current through the inductor is 20.4 mA. To provide an accurate answer, I would need more information about the circuit, such as the values of the resistors, inductor, and any voltage sources. However, I will explain the concept behind the problem.
When the switch is opened after being closed for a long time, the inductor behaves like a current source due to its stored energy. Since the current through the inductor is given as 20.4 mA, the current flowing through R2 will be the same (20.4 mA) immediately after the switch is opened, assuming there are no other current paths in the circuit.
To learn more about values, click here:
brainly.com/question/24503916
#SPJ11
Which value of x is in the domain of f(x) = x - 7? A. X = 8 B. x = -3 C. x = 0 D. x = 6

Answers
the value inside the square root must be positive or zero, then:
x - 7 ≥ 0
x - 7 +7 ≥ 0 + 7 adding 7 at both sides
x ≥ 7
The only option greater than or equal to 7 is 8