Alex house is 15 blocks from school. Carlene lives 7 blocks from Alex's house. Which equation represents the location of Carlene's house in relation to the school?
|x+7|=15
|x-7|=15
|x+15|=7
|x-15|=7
Answers
Answer:
Answer is b
Step-by-step explanation:
Because
|x-7|=15--->x=15+7, x=22Related Questions
PLEASE HELP SMART PEOPLE!
This is add/subtract polynomials.
h(x)+g(x)
h(x)=6x^2+4x^4+7x
Answers
Given,
\(h(x) = {6x}^{2} + {4x}^{4} + 7x\)
\(g( x) = {6x}^{2} - 4x + {3x}^{4} \)
Therefore,
\(h(x) + g(x)\)
\(( {6x}^{2} + {4x}^{4} + 7x) + ({6x}^{2} - 4x + {3x}^{4})\)
\( {6x}^{2} + {4x}^{4} + 7x + {6x}^{2} - 4x + {3x}^{4}\)
\((4 {x}^{4} + 3 {x}^{4} ) + ( {6x}^{2} + {6x}^{2} ) + (7x - 4x)\)
\( {7x}^{4} + {12x}^{2} + 3x\)
Use implicit differentiation to find dy/dx and d^2y/dx^2.

Answers
Using implicit differentiation dy/dx = -(2x + y)/(x + 2y) and d2y/dx² = -2(x² - 3xy - y²)/(x + 2y)³.
Implicit differentiation is the process of differentiating an equation in which it is not easy or possible to express y explicitly in terms of x.
Given the equation x² + xy + y² = 5,
we can differentiate both sides with respect to x using the chain rule as follows:
2x + (x(dy/dx) + y) + 2y(dy/dx) = 0
Simplifying this equation yields:
(x + 2y)dy/dx = -(2x + y)
Hence, dy/dx = -(2x + y)/(x + 2y)
Next, we need to find d^2y/dx^2 by differentiating the expression for dy/dx obtained above with respect to x, using the quotient rule.
That is:
d/dx(dy/dx) = d/dx[-(2x + y)/(x + 2y)](x + 2y)d^2y/dx² - (2x + y)(d/dx(x + 2y))
= -(2x + y)(d/dx(x + 2y)) + (x + 2y)(d/dx(2x + y))
Simplifying this equation yields:
d2y/dx² = -2(x² - 3xy - y²)/(x + 2y)³
For more such questions on implicit differentiation visit:
https://brainly.com/question/25081524
#SPJ8
The height after t seconds of an object projected upward with an initial velocity of 48 feet per second from a 210-foot tower can be modeled by h=−16t^2 + 48t +210. The height of a neighboring 50-foot tall building is modeled by the equation h=50. The time (t) when the object will be at the same height as the building is found to be t = –2 and t =5. Which statement BEST describes the validity of these solutions?
A. Neither solution is valid since time values cannot be squared.
B. The solution t = – 2 is the only solution since 5 seconds is an unreasonable amount of time for the object to reach a height of 50 feet.
C. The solution t = 5 is the only valid solution to this system since time cannot be negative.
D. Both are valid solutions to this system since both values make the equation h=−16t^2 + 48t + 210 true.
Answers
Answer:
C. The solution t = 5 is the only valid solution to this system since time cannot be negative.
Step-by-step explanation:
Given
\(h(t) = -16t^2 + 48t + 210\)
\(h(t) = 50\)
Required
Determine which of the options is true
After solving
\(h(t) = -16t^2 + 48t + 210\)
for
\(h(t) = 50\)
We have that
\(t = -2\) and \(t = 5\)
Because time can't be negative, we have to eliminate \(t = -2\)
So, we're left with
\(t = 5\)
Because of this singular reason, we can conclude that option c answers the question
a chord 7cm long is drawn in a circle of radius 3.7cm. calculate the distance of the chord from the centre of the circle
Answers
Answer: To find the distance of a chord from the center of a circle, we need to use the following formula:
Distance from center = sqrt(r^2 - (c/2)^2)
Where r is the radius of the circle and c is the length of the chord.
In this case, the radius of the circle is 3.7cm and the length of the chord is 7cm.
So, substituting these values in the formula, we get:
Distance from center = sqrt(3.7^2 - (7/2)^2)
= sqrt(13.69 - 12.25)
= sqrt(1.44)
= 1.2 cm
Therefore, the distance of the chord from the center of the circle is 1.2 cm.
Step-by-step explanation:
Findthe
y -intercept
oftheparabolay = x2 + 3x − 6.
Answers
Answer:
(0, -6) is the y-intercept.
whats equivalent to 24+44
Answers
what is 20/3 decimal form
Answers
answer the following questions in the picture

Answers
a. The chart is prepared below.
b. At the end of 4 years, Ross still owes his parents $1,576.92.
How to calculate interest ?To solve this problem, we need to calculate the balance of Ross's loan at the end of each year.
The balance for each year can be calculated by subtracting the yearly payment from the balance at the beginning of the year and adding the interest earned for the year.
The interest for each year is calculated by multiplying the balance at the beginning of the year by the annual interest rate of 3.2%.
Here are the steps for calculating the balance for each year:
Year 1:
Beginning balance = $2,500.00
Interest for the year = $2,500.00 x 0.032 = $80.00
Ending balance = $2,500.00 + $80.00 - $300.00 = $2,280.00
Year 2:
Beginning balance = $2,280.00
Interest for the year = $2,280.00 x 0.032 = $72.96
Ending balance = $2,280.00 + $72.96 - $300.00 = $2,052.96
Year 3:
Beginning balance = $2,052.96
Interest for the year = $2,052.96 x 0.032 = $65.76
Ending balance = $2,052.96 + $65.76 - $300.00 = $1,818.72
Year 4:
Beginning balance = $1,818.72
Interest for the year = $1,818.72 x 0.032 = $58.20
Ending balance = $1,818.72 + $58.20 - $300.00 = $1,576.92
Here's a table that shows the details:
Year ,principal ,Interest rate, interest, Payment ,annual owing
1 $2,500.00 $80.00 $300.00 $2,280.00
2 $2,280.00 $72.96 $300.00 $2,052.96
3 $2,052.96 $65.76 $300.00 $1,818.72
4 $1,818.72 $58.20 $300.00 $1,576.92
b. At the end of 4 years, Ross still owes his parents $1,576.92.
To know more about interest visit:
https://brainly.com/question/30393144
#SPJ1

For the quadratic function f(x) = x2 + 8x + 12 in standard form, find the following key features:
vertex
y-intercept
Roots x =
and x =
Axis of Symmetry x =
Answers
Answer:
vertex:(−4,−4)
y-intercept:(0,12)
roots x=−2
and x= -6
AOS:-4
Step-by-step explanation:
solve the following where a,b and c are constants
2y +z= a
3y +6z=b
Answers
if the question is 2y+3y=a and z+6z=b
then i could solve it otherwise sry
An experiment results in one of three mutually exclusive events A, B, and C. It is known that P(A)= 0.30, P(B) = 0.55, and P(C) = 0.15. Find the following probabilities:
a. P(A∪B)
b. P(A∩C)
c. P(A/B)
d. P(B∪C)
Answers
Answer:
a. P(A∪B)=0.85
b. P(A∩C)=0
c. P(A/B)=0
d. P(B∪C)= 0.70
Step-by-step explanation:
Events are said to be mutually exclusive when both cannot occur simultaneously in the result of experimentation. They are also known as incompatible events.
Being P(A)=0.30, P(B)= 0.55 and P(C)= 0.15
Let A and B be any two events, P (A) and P (B) the probability of occurrence of events A or B, is known as the probability of union [denoted as P (A U B)]:
P(A∪B)=P(A) + P(B) - P(A∩B)
Mutually exclusive events are results of an event that cannot occur at the same time. So:
P(A∩B)=0 That is, there is no chance that both events will occur.
So: P(A∪B)=P(A) + P(B)
In this case: P(A∪B)=P(A) + P(B)= 0.30 + 0.55 → P(A∪B)=0.85
As mentioned, if two events are mutually exclusive, there is no chance that both events will occur. Being the intersection an operation whose result is made up of the non-repeated and common events of two or more sets, that is, given two events A and B, their intersection is made up of the elementary events that they have in common, then: P(A∩C)=0
The probability that event A will occur if event B has occurred is called the conditional probability and is defined:
P(A/B)=P(A∩B)÷P(B) being P(B)≠0
Since A and B are mutually exclusive, P (A∩B) = 0. So:
P(A/B)=P(A∩B)÷P(B)=0÷0.55 → P(A/B)=0
Finally, P(B∪C)=P(B) + P(C) - P(B∩C)
Since A and B are mutually exclusive, P (B∩C) = 0. So:
P(B∪C)=P(B) + P(C)= 0.55 + 0.15 → P(B∪C)= 0.70
restaurants frequently add an 18% tip on the pre tax when the party is 8 or more people. the tax is calculated based on the bill before tip is included. last night, 12 friends went out to dinner and decided to split the bill evenly. if the bill without tax or tip was $105.89 and tax was 5%. how much did each person owe
Answers
The money each person owed is $10.853725 if the cost of the meal without tax or tip is $105.89.
What is meant by Percentage?Percentage is defined as the parts of a number per fraction of 100. It is denoted by the symbol '%'.
We can calculate percentage of a number by dividing a number with it's whole and then multiply with 100.
Given,
Cost of the meal before tax or tip = $105.89
Amount of tip = 18% of $105.89
= 18% × 105.89
= 0.18 × 105.89
= $19.0602
Amount of tax = 5% of $105.89
= 5% × 105.89
= 0.05 × 105.89
= $5.2945
Total cost for the meal = $105.89 + $19.0602 + $5.2945
= $130.2447
Total number of friends = 12
Money owed by each friend = $130.2447 / 12
= $10.853725
Hence the money owed by each is $10.853725.
Learn more about Percentage here :
https://brainly.com/question/16637207
#SPJ9
As the earth revolves around the sun, it travels at a speed of approximately 18 miles per second. Convert this speed to kilometers per second. At this speed, how many kilometers will the earth travel in 2 seconds? In your computations, assume that 1 mile is equal to 1.6 kilometers. Do not round your answer.
Answers
Answer:
i dont know have an amazing day
Step-by-step explanation:
be kind ppl
Joey is flying his Cesna due Northwest at 188mph. Unfortunately, a wind traveling.
60mph due 150 bearing. Find Joey's actual Speed and direction.
Answers
Joey's actual speed is 143.59 mph, and his actual direction is slightly west of northwest.
Given that Joey's aircraft speed: 188 mph
Wind speed: 60 mph
Wind direction: 150 degrees (measured clockwise from due north)
We can consider the wind as a vector, which has both magnitude (speed) and direction.
The wind vector can be represented as follows:
Wind vector = 60 mph at 150 degrees
We convert the wind direction from degrees to a compass bearing.
Since 150 degrees is measured clockwise from due north, the compass bearing is 360 degrees - 150 degrees = 210 degrees.
Joey's aircraft speed vector = 188 mph at 0 degrees (due northwest)
Wind vector = 60 mph at 210 degrees
To find the resulting velocity vector, we add these two vectors together. This can be done using vector addition.
Converting the wind vector into its x and y components:
Wind vector (x component) = 60 mph × cos(210 degrees)
= -48.98 mph (negative because it opposes the aircraft's motion)
Wind vector (y component) = 60 mph×sin(210 degrees)
= -31.18 mph (negative because it opposes the aircraft's motion)
Now, we can add the x and y components of the two vectors to find the resulting velocity vector:
Resulting velocity (x component) = 188 mph + (-48.98 mph) = 139.02 mph
Resulting velocity (y component) = 0 mph + (-31.18 mph) = -31.18 mph
Magnitude (speed) = √((139.02 mph)² + (-31.18 mph)²)
= 143.59 mph
Direction = arctan((-31.18 mph) / 139.02 mph)
= -12.80 degrees
The magnitude of the resulting velocity vector represents Joey's actual speed, which is approximately 143.59 mph.
The direction is given as -12.80 degrees, which indicates the deviation from the original northwest direction.
To learn more on Speed click:
https://brainly.com/question/28224010
#SPJ1
Find a and b using the factor theorem.
\(f(x)=x^3+ax^2+bx-12\) has factor \((x-1), (x+1)\)
Answers
The values of a and b using the factor theorem for the polynomial f(x), we set f(1) and f(-1) equal to zero. Solving the resulting system of equations, we find that a = 12 and b = -1.
To find the values of a and b using the factor theorem, we need to use the given factors (x - 1) and (x + 1) and the fact that they are roots of the polynomial f(x).
The factor theorem states that if (x - c) is a factor of a polynomial, then f(c) = 0. Therefore, we can set x = 1 and x = -1 in the polynomial f(x) to get two equations.
First, let's substitute x = 1 into f(x):
f(1) = (1)^3 + a(1)^2 + b(1) - 12
f(1) = 1 + a + b - 12
Next, let's substitute x = -1 into f(x):
f(-1) = (-1)^3 + a(-1)^2 + b(-1) - 12
f(-1) = -1 + a - b - 12
Since (x - 1) and (x + 1) are factors, f(1) and f(-1) must equal zero. Therefore, we can set the two equations equal to zero and solve for a and b:
1 + a + b - 12 = 0
-1 + a - b - 12 = 0
Rearraning the equations, we have:
a + b = 11
a - b = 13
Now, we can solve this system of equations. Adding the two equations, we get:
2a = 24
a = 12
Substituting the value of a into one of the equations, we find:
12 - b = 13
b = -1
Therefore, the values of a and b are 12 and -1 respectively.
For more such questions on polynomial
https://brainly.com/question/1496352
#SPJ8
Which function of the S&P Capital IQ Excel plug-in allows users to extract company data directly from CapIQ’s database and calculate the desired financial metrics using the CapIQ formulas?
Review Later
Formula Builder
Auditing
Screening
Templates
Answers
The function of the S&P Capital IQ Excel plug-in allows users to extract company data directly from CapIQ’s database and calculate the desired financial metrics using the CapIQ formulas is; Formula Builder
What is the financial tool used?S&P Capital IQ Excel plug is a tool that helps to provide access to financial data, news and analytics for real estate investment trusts (REITs) including other industry data on bank & thrifts, financial services, insurance, real estate and other markets.
Now, when the Excel Plug-in has been installed, a new toolbar will be
available in Excel. This toolbar is called formula builder and it is useful for the following use in S&P Capital;
Enable/Disable the Excel Plug-inSearch any company financialsSearch for formulasBuild formulasCreate comp setsGo to saved screensAccess chartingRefresh dataOpen the S&P Capital IQ platform in a browserOpen S&P Capital IQ’s screening pageAccess filingsRead more about Financial Tool at; https://brainly.com/question/14364696
#SPJ1
-8(-x - 5) - 2 = -2 (x + 1)
Answers
Answer:
-8(-x-5)-2 = -2 (x+1)
8x + 40 -2 = -2x -2
8x + 2x = -2 -40 +2
10x = -40
x = -40/10
x = -4
Solve (t-3)^2=6
The arrow is at a height of 48 ft after approx. ___ s and after ___ s.
Answers
The arrow is at a height of 48 ft after approx. 3 - √6 s and after 3 + √6 s.
To find the time it takes for the arrow to reach a height of 48 ft, we can use the formula for the height of the arrow:
s = v0t - 16t^2
Here, s represents the height of the arrow, v0 is the initial velocity, and t is the time.
Given that the initial velocity, v0, is 96 ft/s and the height, s, is 48 ft, we can set up the equation:
48 = 96t - 16t^2
Now, let's solve this equation to find the time it takes for the arrow to reach a height of 48 ft.
Rearranging the equation:
16t^2 - 96t + 48 = 0
Dividing the equation by 16 to simplify:
t^2 - 6*t + 3 = 0
We now have a quadratic equation in the form of at^2 + bt + c = 0, where a = 1, b = -6, and c = 3.
Using the quadratic formula:
t = (-b ± √(b^2 - 4ac)) / (2a)
Plugging in the values:
t = (6 ± √((-6)^2 - 413)) / (2*1)
t = (6 ± √(36 - 12)) / 2
t = (6 ± √24) / 2
Simplifying the square root:
t = (6 ± 2√6) / 2
t = 3 ± √6
Therefore, the arrow reaches a height of 48 ft after approximately 3 + √6 seconds and 3 - √6 seconds.
In summary, the arrow takes approximately 3 + √6 seconds and 3 - √6 seconds to reach a height of 48 ft, assuming an initial velocity of 96 ft/s.
For more question on height visit:
https://brainly.com/question/28990670
#SPJ8
Note the complete question is
The height of an arrow shot upward can be given by the formula s = v0*t - 16*t², where v0 is the initial velocity and t is time.How long does it take for the arrow to reach a height of 48 ft if it has an initial velocity of 96 ft/s?
Solve (t-3)^2=6
The arrow is at a height of 48 ft after approx. ___ s and after ___ s.
The propellers on the Titanic have a radius of 23.5 ft and weigh 38 tons each. If the propellers turn at 180 rpm, what would be the angular speed of a blade in radians per second?
Answers
Answer:
Hahahahahahahahahahhahahahahaha
Find the unit price of each of the following items. Round your answer to the nearest tenth.
jelly
18 oz at $1.36
32 oz at $2.03
Answers
Answer:
$0.0756 for 18 oz
$0.0634 for 32 oz
Step-by-step explanation:
In class, we developed the formula
(a) Use the formula (using appropriate substitutions) to find the closed form for ∑2
= 2
(b) Use the formula in the notes for ∑
= 13 to find the closed form expression form for
∑
= 3 (assume a ≥ 1 and a ≤ b)
(c) In class, we developed the formula
Use this formula and some algebra to derive a closed form for the sum ∑
= 0( ― 1)2 ― 1
(d) Test your closed form solution in (c) to find the value of ∑3
= 0( ― 1)2 ― 1 and see if
it matches the manual computation of the 4 terms of the sum.
Answers
(a) The closed form for ∑2 is 2.
(b) The closed form expression for ∑3 is 24.
(c) The closed form for the sum ∑n = 0(― 1)² ― 1 is n(1 - n) / 2.
(d) The value of -3 matches the manual computation of the four terms.
Our closed form solution is correct.
To find the closed form for ∑2, we can use the formula for the sum of the first n terms of an arithmetic series:
∑2 = n(a + l) / 2
In this case, a = 2 (the first term) and l = 2 (the last term) since we are summing a series of 2's.
We also know that there is only one term, so n = 1.
Substituting these values into the formula, we have:
∑2 = 1(2 + 2) / 2
= 4 / 2
= 2
The formula for the sum of the first n terms of an arithmetic series is:
∑n = n(a + l) / 2
In this case, we have a = 3 (the first term), l = 13 (the last term), and n = 3 (the number of terms).
Substituting these values into the formula, we get:
∑3 = 3(3 + 13) / 2
= 3(16) / 2
= 48 / 2
= 24
The formula we developed in class is:
∑n = n(a + a + (n - 1)d) / 2
In this case, we have a = 0 (the first term) and d = -1 (the common difference).
Substituting these values into the formula, we get:
∑n = n(0 + 0 + (n - 1)(-1)) / 2
= n(0 - n + 1) / 2
= n(1 - n) / 2
To test the closed form solution for ∑3 = 0(― 1)² ― 1, we substitute n = 3 into the closed form expression we derived in part (c):
∑3 = 3(1 - 3) / 2
= 3(-2) / 2
= -6 / 2
= -3
Now, let's manually compute the sum of the first four terms of ∑3 = 0(― 1)² ― 1:
0(― 1)² ― 1 + 1(― 1)² ― 1 + 2(― 1)² ― 1 + 3(― 1)² ― 1
= 0 - 1 - 2 - 3
= -6
For similar questions on manual computation
https://brainly.com/question/32637761
#SPJ8
can someone please help me? I'm really confused and I don't know how to do this.
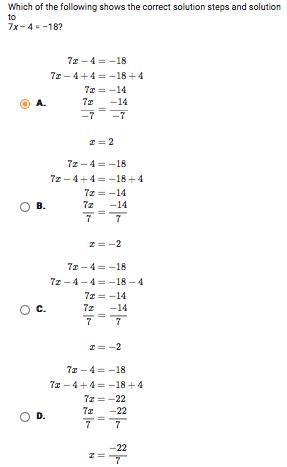
Answers
Answer:
B
Step-by-step explanation:
Because they took the correct steps to answer the equation.They also got the right answer (-2).
At the begining they added 4 to both sides (to cancel out the 4)
C would be wrong because they subtracted 4 from a negative four and this does NOT cancel it out.
Have a Supercalifragilisticexpialidocious day, I hope you like my explination. If you do please give rating or brainliest :)
What is the value of y?

Answers
Answer:
\( \boxed{D. \: 40\degree} \)
Step-by-step explanation:
Angle sum property of triangle states that the sum of interior angles of a triangle is 180°
So,
\( = > 2y \degree + (y + 10)\degree + 50\degree = 180\degree \\ \\ = > 2y\degree + y\degree + 10\degree + 50\degree = 180\degree \\ \\ = > 3y\degree + 60\degree = 180\degree \\ \\ = > 3y\degree = 180\degree - 60\degree \\ \\ = > 3y\degree = 120\degree \\ \\ = > y = \frac{120\degree}{3\degree} \\ \\ = > y = 40\degree \)
Find the equation of the line.
Use exact numbers.

Answers
Answer:
Step-by-step explanation:

Question Complete the square to make a perfect square trinomial. Then, write the result as a binomial squared. 2n n- + 3 21answer formatn^2 + 2n/3 +___ =(___)^2
Answers
the formula is
\((a+b)^2=a^2+2ab+b^2\)follow this
\(n^2+\frac{2n}{3}+\frac{1}{9}=\mleft(n+\frac{1}{3}_{}\mright)^2\)The distance from the tip of a slice of pizza to the crust is 7 inches.
Does this represent diameter, circumference, or radius?
ANSWER ASAP THANK YOU
Answers
Answer:
radius
Step-by-step explanation:
(8 points) will mark brainliest!! pls help:)

Answers
Answer:
-0.366666666667
Step-by-step explanation:
that's what you get when you divide -22/5 (-4 2/5) by 4/3 (1 1/3)
Answer:
-24/5 is the correct answer.
Steps:
1) -4 x 2/5 = -8/5
2) 1 x 1/3 = 1/3
3) -8/5 : 1/3 = -24/5
In 2000, an estimated 7.7 x 10^7 spoke French as their first language and an estimated 1 x 10^8 people spoke German as their first language. In 2000, which language had more speakers?
Answers
Answer:
German
Step-by-step explanation:
Given :
Number of people who spoke French as first language in 2000 = 7.7 * 10^7 ; in standard form ;
7.7 * 10^7 = 7.7 * (10 * 10* 10 * 10* 10* 10 * 10) = 77,000,000 = 77 million
Number of people who spoke German as first language in 2000 = 1 * 10^8 ; in standard form ;
1 * 10^8 = 1 * (10 * 10* 10 * 10* 10* 10 * 10 * 10) = 100,000,000 = 100 million
German had more speakers
Help me please please

Answers
Answer:
1/16
if u need an explanation just ask in the comments!
For the polynomial function ƒ(x)= −2x2 − 4x + 16, find all local and global extrema.
Answers
For the given quadratic equation we only have a maximum at y = 18.
How to find the extrema of the given function?
Here we have:
\(f(x) = -2x^2 - 4x + 16\)
Notice that this is a quadratic equation of negative leading coefficient.
Then we have a maximum at the vertex, and both arms tend to negative infinity as x tends to infinity or negative infinity.
The vertex is at:
x = -(-4)/(2*(-2)) = -1
The maximum is:
\(f(-1) = -2*(-1)^2 - 4*(-1) + 16 = -2 + 4 + 16 = 18\)
If you want to learn more about quadratic equations:
https://brainly.com/question/1214333
#SPJ1