According to a report for veterinarians in the united states, 36. 5 percent of households in the united states own dogs and 30. 4 percent of households in the united states own cats. If one household in the united states is selected at random, what is the probability that the selected household will own a dog or a cat?.
Answers
Related Questions
Question 1
Which classification(s) describe the figure above? Explain your answer in the space provide
1. Quadrilateral
II. Rectangle
III. Parallelogram
IV. Rhombus
Answers
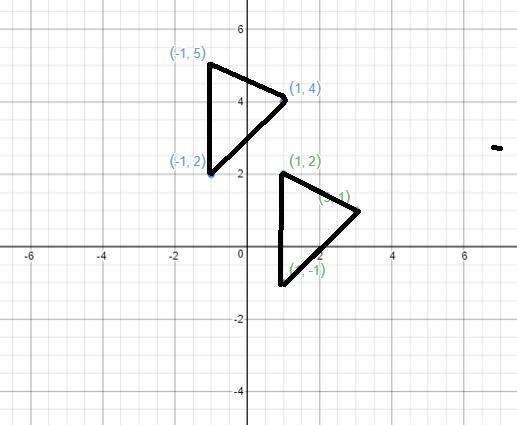
The vertices of a triangle are A(1, 2) , B(3, 1) and C(1,- 1) . Draw the figure and its image after the translation ( x - 2 . y + 3 )
Answers
The triangle and its image are added as attachment
How to determine the image of the triangleFrom the question, we have the following parameters that can be used in our computation:
A(1, 2) , B(3, 1) and C(1,- 1)
Also, we have
The translation ( x - 2 . y + 3 )
To perform a translation on a figure, we need to add -2 to the x-coordinate and 3 to the y-coordinate of each point.
i.e.
(x, y) = ( x - 2 . y + 3 )
So, we have
A(1 - 2, 2 + 3) , B(3 - 2, 1 + 3) and C(1 - 2,- 1 + 3)
This gives
A'(-1, 5), B'(1, 4), and C'(-1, 2).
See attachment for the figure
Read more about transformation at
https://brainly.com/question/27224272
#SPJ1
Two joggers run 8 miles and then 5 miles west. What is the shortest distance, to the nearest tenth of a mile they must travel to return to their starting position?

Answers
Answer:
A. 9.4 mi
Step-by-step explanation:
Sketch a right triangle with legs of 8 and 5. Shortest distance back to the starting point is the hypotenuse (h) of the triangle:
h² = 8² + 5² = 89
h = √89 = 9.43 mi
14n + 34 = 2(17 + 7n)
Answers
Answer:
n = infinite amount of solutions
General Formulas and Concepts:
Pre-Alg
Order of Operations: BPEMDASEquality PropertiesStep-by-step explanation:
Step 1: Define equation
14n + 34 = 2(17 + 7n)
Step 2: Solve for n
Distribute 2: 14n + 34 = 34 + 14nSubtract 34 on both sides: 14n = 14nDivide both sides by 14: n = nHere we see that n can be any number. Therefore, n has an infinite amount of solutions.
let a and b be integers. prove that if ab = 4, then (a – b)3 – 9(a – b) = 0.
Answers
Let \(\(a\)\) and \(\(b\)\) be integers such that \(\(ab = 4\)\). We want to prove that \(\((a - b)^3 - 9(a - b) = 0\).\)
Starting with the left side of the equation, we have:
\(\((a - b)^3 - 9(a - b)\)\)
Using the identity \(\((x - y)^3 = x^3 - 3x^2y + 3xy^2 - y^3\)\), we can expand the cube of the binomial \((a - b)\):
\(\(a^3 - 3a^2b + 3ab^2 - b^3 - 9(a - b)\)\)
Rearranging the terms, we have:
\(\(a^3 - b^3 - 3a^2b + 3ab^2 - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\(a^3 - b^3 - 3a^2(4) + 3a(4^2) - 9a + 9b\)\)
Simplifying further, we get:
\(\(a^3 - b^3 - 12a^2 + 48a - 9a + 9b\)\)
Now, notice that \(\(a^3 - b^3\)\) can be factored as \(\((a - b)(a^2 + ab + b^2)\):\)
\(\((a - b)(a^2 + ab + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Simplifying further, we get:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\)
Now, we can observe that \(\(a^2 + 4 + b^2\)\) is always greater than or equal to \(\(0\)\) since it involves the sum of squares, which is non-negative.
Therefore, \(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\) will be equal to \(\(0\)\) if and only if \(\(a - b = 0\)\) since the expression \(\((a - b)(a^2 + 4 + b^2)\)\) will be equal to \(\(0\)\) only when \(\(a - b = 0\).\)
Hence, we have proved that if \(\(ab = 4\)\), then \(\((a - b)^3 - 9(a - b) = 0\).\)
To know more about satisfies visit-
brainly.com/question/16993710
#SPJ11
Express the interval shown on the number line in inequality notation.
G
T-
10 12
-12
-6
6
-10
8
-8
-2 0
24
-4
A
U
>>
Al
00
IA
00
or
D.
[]
(,) || ()
I
Inequality Notation:
](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/yV3Bk2LZ34JUHeKQufHmUxCwYL45P6bM.png)
Answers
Answer:
Umm Where's The Answer?
Simplify (r4)6
..............:::::::.......

Answers
Answer: The second r10
Step-by-step explanation:
in how many years will rupees 1200 at the rate of 15% interest amount to 1740
Answers
Answer: 3 years
Step-by-step explanation:
Interest = 1740 - 1200 = 540
SI = prt / 100
540 = 1200 x 0.15 x t
540 = 180t
t = 540 / 180 = 3
Find the interest amount.
\(I=1740-1200=540\)
Use the formula for simple interest.
\(I=prt/100\)
Solve for t.
\(540=1200 \times 15\% \times t\)
\(540=1200 \times \frac{15}{100} \times t\)
\(540=180t\)
\(t=\frac{540}{180}\)
\(t=3\)
3 years.What is the coefficient of the second term of the trinomial? (6p 2)2=36p2 Bp 4 Enter your answer in the box. B =.
Answers
Answer:the coefficient of the 2nd term is : 24
Step-by-step explanation:(6p + 2)^2 =
(6p + 2)(6p + 2) =
36p^2 + 12p + 12p + 4 =
36p^2 + 24p + 4
how can you reflect a point over the y axis without graphing it?
Answers
Answer: You switch the point in the x-axis to the negative/positive of the number.
Step-by-step explanation:
So for example if you have the point (3,7), you would switch the 3 to -3 and you would keep the y the same.
Hope this helps!
a small jet can carry up to passengers and crew members. there is a weight restriction of pounds on board. the combined weight of each passenger (or crew member) and his luggage has a mean of pounds, with a standard deviation of pounds. what is the probability that the weight limit will be exceeded when there are exactly passengers and crew members on board?
Answers
The probability that the weight limit will be exceeded when there are exactly 40 passengers and 3 crew members on board is 0.031.
Mean = 196 × 43
Mean = 8428
Std. Dev. = 63 × √(43)
Std. Dev. = 63 × 6.56
Std. Dev. = 413.28
Here, μ = 8428, σ = 413.1186 and x = 9200. We must calculate P(X ≥ 9200).
he central limit theorem states that, for a sufficiently large sample size, the sample mean of all observations will be approximately normally distributed, regardless of the distribution of the population from which it was sampled.
The Central Limit Theorem is used to get the associated z-value.
z = (x - μ)/σ
z = (9200 - 8428)/413.28
z = 772/413.28
z = 1.87
Therefore,
P(X ≥ 9200) = P(z ≤ (9200 - 8428)/413.1186)
P(X ≥ 9200) = P(z ≤ 772/413.1186)
P(X ≥ 9200) = P(z ≥ 1.87)
P(X ≥ 9200) = 1 - 0.9693
P(X ≥ 9200) = 0.031
To learn more Central Limit Theorem link is here
brainly.com/question/18403552
#SPJ4
The complete question is:
A small jet can carry up to 40 passengers and 3 crew members. There is a weight restriction of 9200 pounds on board. The combined weight of each passenger (or crew member) and his luggage has a mean of 196 pounds, with a standard deviation of 63 pounds. What is the probability that the weight limit will be exceeded when there are exactly 40 passengers and 3 crew members on board? Carry your intermediate computations to at least four decimal places. Report your result to at least three decimal places.
What is the volume of the rectangular prism?
I need a lot of help bro

Answers
Help me pleaseeeeeeeeeee

Answers
Answer:
I'm pretty sure it's a
Step-by-step explanation:
step by step
100 points and brainliest!!!

Answers
Answer:
below
Step-by-step explanation:
1. 35910 (190*189)
2. 343 possibilities
Answer:
1. 35910 (190*189)
2. 343 possibilities
The equation of a parabola is y=2x^2 +8x +3
Write the equation in vertex form and show your work.
Answers
Answer: y = 2(x + 2)² - 5
Step-by-step explanation:
We are going to use the completing the square method to transform this quadratic equation from standard form to vertex form.
Given:
y = 2x² + 8x + 3
Factor the 2 out of the first two terms:
y = 2(x² + 4x) + 3
Add and subtract \(\frac{b}{2} ^2\):
y = 2(x² + 4x + 4 - 4) + 3
Distribute the 2 into -4 and combine with the 3:
y = 2(x² + 4x + 4) - 5
Factor (x² + 4x + 4):
y = 2(x + 2)² - 5
Help me with this
Please no fake answers

Answers
Answer:
*inserting real answer*
The answer I think is A which is \(4r^{2}\)
Step-by-step explanation:
Hope this helps have a nice day!
Also to let you know I tried my best ok ;-;
Suppose you have a job that pays $13.50 per hour and you work anywhere from 10 to 40 hours per week. a. Write an equation, with a restriction on the variable I, that gives the amount of money, y, you will earn for working 2 hours in one week. y = _____ , Preview with ____ <= x <= ____ b. Use the function rule you have written in part a. to find the y values for the given z values: x = 10, y = ___ x = 20, y= ___
x = 30, y = ____. x = 40, y = ____ c. Construct a line graph from the information found in b. 520+ -480+ 440+ 400- 360 320- 280- 240 200 160+ 120+ 80- 40+ 10 20 30 40 Clear All Draw: Line Dot Open Dot d. State the domain and range of this function. Domain: ____ <= x <= ______
Range: <= y <= _____
e. What is the minimum amount you can earn in a week with this job? You'll earn at least $ ______.
What is the maximum amount? You can earn up to $ ____.
Answers
The maximum amount you can earn is $540
a. y = 13.50x , 10 <= x <= 40
b. x = 10, y = 135; x = 20, y= 270; x = 30, y = 405; x = 40, y = 540
c. Domain: 10 <= x <= 40; Range: 0 <= y <= 540
d. The minimum amount you can earn in a week with this job is $135. The maximum amount you can earn is $540.
To learn about Domain
brainly.com/question/29452843
#SPJ11
If y=3x+5 and z=x^2+2x-5, what is yz?
Answers
Work Shown:
yz = y(x^2+2x-5)
yz = y(x^2) + y(2x) + y(-5)
yz = x^2( y ) + 2x( y ) - 5( y )
yz = x^2( 3x+5 ) + 2x( 3x+5 ) - 5( 3x+5 )
yz = x^2*3x + x^2*5 + 2x*3x + 2x*5 - 5*3x - 5*5
yz = 3x^3 + 5x^2 + 6x^2 + 10x - 15x - 25
yz = 3x^3 + 11x^2 - 5x - 25
the numbers of hours worked (per week) by 400 statistics students are shown below. number of hours frequency 0 - 9 20 10 - 19 80 20 - 29 200 30 - 39 100 the cumulative percent frequency for the class of 30 - 39 is
Answers
The cumulative percent frequency for the class of 30 - 39 hours worked per week, among 400 statistics students, is 70%.
To find the cumulative percent frequency for the class of 30 - 39 hours worked per week, we need to calculate the cumulative frequency first. The cumulative frequency represents the sum of frequencies up to a certain class.
In this case, we start with the frequency of the first class, which is 20. Then we add the frequency of the second class, which is 80, to get a cumulative frequency of 100. Next, we add the frequency of the third class, which is 200, to get a cumulative frequency of 300. Finally, we add the frequency of the fourth class, which is 100, to get a cumulative frequency of 400.
To calculate the cumulative percent frequency, we divide the cumulative frequency for the class of 30 - 39 (which is 300) by the total number of observations (400) and multiply by 100. This gives us (300/400) * 100 = 75%. Therefore, the cumulative percent frequency for the class of 30 - 39 is 75%.
Learn more about statistics here:
https://brainly.com/question/32201536
#SPJ11
Please help ASAP and please show work if possible.

Answers
Answer:
72° and 108°
Step-by-step explanation:
let one angle be x then the other angle is 1.5x
A linear pair sum to 180° , so
x + 1.5x = 180 , that is
2.5x = 180 ( divide both sides by 2.5 )
x = 72
1.5x = 1.5 × 72° = 108°
The two angles are 72° and 108°
Answer:
do you have wazapp I can send full pic of the answer here
Use the equation below to find y, if m=5, x=6, and b= 12.
y=mx-b
Answers
Answer:118
Step-by-step explanation:
Y= mx-b ....substitute the values of m,x,b
Y=(5×6)-12
y= 30-12
Y=118
A line with a slope of –1/4 passes through the point (–6,5). What is its equation in point-slope form?
Answers
The point- slope form of the line is y-5 = -0.25(x+6).
What is line?
A line is an one-dimensional figure. It has length but no width. A line can be made of a set of points which is extended in opposite directions to infinity. There are straight line, horizontal, vertical lines or may be parallel lines perpendicular lines etc.
A line with a slope of –1/4 passes through the point (–6,5)
Any line in point - slope form can be written as
y - y₁= m(x -x₁) -------(1)
where,
y= y coordinate of second point
y₁ = y coordinate of first point
m= slope of the line
x= x coordinate of second point
x₁ = x coordinate of first point
In the given problem (x₁ , y₁) = (-6,5) and m= -1/4
Putting all these values in equation (1) we get,
y-5= (-1/4) (x- (-6))
⇒ y-5 = -0.25(x+6)
Hence, the point- slope form of the line is y-5 = -0.25(x+6).
To know more about line
brainly.com/question/13763238
#SPJ1
what percentage of persons who lose weight are able to maintain it for more than a year?
Answers
Answer: 20%
Step-by-step explanation:
the R9000 invested at 8%p.a simple interest for 3years show all the steps
Answers
Answer:
To calculate the interest earned on the R9000 invested at 8%p.a simple interest for 3 years, you'll need to use the formula I = Prt.
I = Interest earned
P = Principal amount (R9000)
r = Rate of interest (8% = 0.08)
t = Time (3 years)
Plugging in the values, we get: I = 9000 x 0.08 x 3 = R2160.
Therefore, the interest earned on the R9000 invested at 8%p.a simple interest for 3 years is R2160.
Solve negative four and one fifth ÷ two and one fourth.
one and 39 over 45
negative one and 39 over 45
negative eight and one twentieth
negative nine and 9 over 20
Answers
Solving the fraction negative four and one fifth ÷ two and one fourth gives; negative one and 39 over 45
How to divide fractions?We want to divide the fraction negative four and one fifth ÷ two and one fourth. This can be expressed as;
-4¹/₅ ÷ 2¹/₄
Converting to improper fraction gives;
-21/5 ÷ 9/4
= -21/5 * 4/9
= -84/45
3 is a common factor that both numerator and denominator can be divided by to get; -28/15
Expressing the answer as a mixed fraction is; -1 ³⁹/₄₅
Read more about dividing fractions at; https://brainly.com/question/1622425
#SPJ1
ms. wood has a collection of 25 questions. how many different tests of 5 questions each can be made from the set of questions?
Answers
There are 25,053,600 different tests of 5 questions each that can be made from Ms. Wood's collection of 25 questions.
To find the number of different tests of 5 questions each that can be made from a set of 25 questions, you can use the combination formula. The combination formula is:
n! / (r! * (n-r)!)
Where n is the total number of items and r is the number of items being chosen at a time.
In this case, n is 25 (the total number of questions) and r is 5 (the number of questions per test). Plugging these values into the formula gives:
25! / (5! * (25-5)!) = 25! / (5! * 20!) = 25 * 24 * 23 * 22 * 21 / (5 * 4 * 3 * 2 * 1) = 25,!053,!600
To know more about combination formula visit :
brainly.com/question/14685054
#SPJ4
2 diagonals of a regular nonagon (a 9-sided polygon) are chosen. What is the probability that their intersection lies inside the nonagon
Answers
The probability of the intersection of the two diagonals chosen lying inside the nonagon is 2/3.
What is the probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, with 0 representing an impossible event and 1 representing a certain event.
In this problem, the event of interest is the intersection of the two diagonals lying inside the nonagon. A nonagon is a 9-sided polygon, so there are 9 total corners, each of which can be one end of a diagonal. Therefore, there are 9 choose 2 = 36 total ways to choose two diagonals.
To find the number of favorable outcomes, we need to find the number of ways to choose two diagonals such that their intersection is inside the nonagon. To do this, we can notice that the diagonals that have an intersection inside the nonagon are the diagonals that connect non-adjacent corners of the nonagon. There are 8 non-adjacent corners, so there are 8 choose 2 = 28 ways to choose two non-adjacent corners.
So the probability of the intersection of the two diagonals lying inside the nonagon is:
P(intersection inside nonagon) = favorable outcomes / total outcomes = 28/36 = 2/3
Hence, the probability of the intersection of the two diagonals chosen lying inside the nonagon is 2/3.
To learn more about the probability, visit:
https://brainly.com/question/24756209
#SPJ4
The probability of the intersection of the two diagonals chosen lying inside the nonagon is 2/3.
What is the probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, with 0 representing an impossible event and 1 representing a certain event.
In this problem, the event of interest is the intersection of the two diagonals lying inside the nonagon. A nonagon is a 9-sided polygon, so there are 9 total corners, each of which can be one end of a diagonal. Therefore, there are 9 choose 2 = 36 total ways to choose two diagonals.
To find the number of favorable outcomes, we need to find the number of ways to choose two diagonals such that their intersection is inside the nonagon. To do this, we can notice that the diagonals that have an intersection inside the nonagon are the diagonals that connect non-adjacent corners of the nonagon. There are 8 non-adjacent corners, so there are 8 choose 2 = 28 ways to choose two non-adjacent corners.
So the probability of the intersection of the two diagonals lying inside the nonagon is:
P(intersection inside nonagon) = favorable outcomes / total outcomes = 28/36 = 2/3
Hence, the probability of the intersection of the two diagonals chosen lying inside the nonagon is 2/3.
To learn more about the probability, visit:
brainly.com/question/24756209
#SPJ4
f(x)=3x+5 and g(x)=2x+1
value of x
Answers
You can treat x and 2x+1 just as though they are real numbers.
So f(2x+1) = 3(2x+1) - 5 = 6x + 3 - 5 = 6x - 2
In the above, I made use of something called the distributive law which says that if a,b and c are real numbers, then a(b+c) = ab + ac.
mDEG
Solve for the indicated measure. Do not type degree
symbol in your answer.
Answer
84
57
70
59
areDEG=

Answers
If x and y vary inversely and x = 5 when y = -3.5, what is the value of x when y = 10?
Answers
Answer:
Step-by-step explanation:
k = xy
Putting values of x and y in the equation
k = (5)(-3.5)
= - 17.5
Finding value of x when y = 10
k = xy
- 17.5 = x10
Bringing like terms on one side
- 17.5 - 10 = x
-27.5 = x