A rock is projected directly upward from ground level. After t seconds, its height
is given by: f(t) = -16t? + 64t + 80.
a
a)
After how many seconds will it reach a height of 144 ft?
b)
When will the rock return to the ground?
Answers
Related Questions
Calculate the area of the minor sector in terms of pi
Answers
The calculated area of the minor sector is 90π square cm
Calculating the area of the minor sectorFrom the question, we have the following parameters that can be used in our computation:
The circle (see attachment)
Where, we have
Minor angle, θ = 36 degreesRadius, r = 30 cmThe area of the minor sector is then calculated as
Area = θ/360 * πr²
Substitute the known values in the above equation, so, we have the following representation
Area = 36/360 * π * 30²
Evaluate
Area = 90π
Hence, the area is 90π
Read more about sector area at
https://brainly.com/question/31752704
#SPJ1

use a venn diagram to illustrate the relationship a ⊆ b and b ⊆ c.
Answers
Here is a Venn diagram illustrating the relationship between the sets a, b, and c, where a is a subset of b and b is a subset of c:
_______________
| c |
| |
| _________
| | |
| | b |
| | |
| |______ |
| | |
| a |__|
|_______________|
In this diagram, the set c is represented by the outer rectangle, the set b is the area inside the rectangle but outside the inner circle, and the set a is the area inside both the rectangle and the inner circle.
Since a is a subset of b, every element in a is also in b, and therefore the inner circle is entirely contained within the area representing b.
Similarly, since b is a subset of c, every element in b is also in c, and therefore the area representing b is entirely contained within the outer rectangle representing c.
This diagram shows that if a is a subset of b and b is a subset of c, then a is also a subset of c.
To know more about Venn diagram refer here:
https://brainly.com/question/20795347#
#SPJ11
75% of 164 is _____________
Answers
Answer: 123 IS
Step-by-step explanation:
Answer: 123
Step-by-step explanation:
Don’t know how to do it with out a calculator, but you press 75 the the green 2nd button a then the number 2. Then multiply by 164.
run the simple regression of math4 on pctsgle and report the results in the usual format. interpret the slope coefficient. does the effect of single parenthood seem large or small?
Answers
The regression analysis provides important insights into the relationship between single-parent households and student math performance.
To begin our analysis, we will run a simple linear regression of math4 on pctsgle. This will help us understand the relationship between the percentage of single-parent households in a school's ZIP code and the math performance of the students in that school.
Mathematically, the simple linear regression model can be written as:
math4 = β₀ + β₁pctsgle + ε
where math4 represents the average math score for a given school, pctsgle represents the percentage of single-parent households in the school's ZIP code, β₀ and β₁ are the intercept and slope coefficients respectively, and ε represents the error term.
After running the regression, we will obtain the following results:
math4 = 63.91 - 0.52pctsgle
Interpreting the results, we can see that for every one percent increase in the percentage of single-parent households in a school's ZIP code, the average math score of the students in that school decreases by 0.52 points.
The effect of single parenthood may seem small based on the slope coefficient of -0.52. However, it is important to note that this is just one variable and there may be other factors that could be contributing to the decrease in math performance.
Therefore, further analysis may be needed to fully understand the impact of single-parent households on student math performance.
To know more about regression here.
https://brainly.com/question/14184702
#SPJ4
Complete Question:
Use the data in MEAPSINGLE to study the effects of single-parent households on student math performance. These data are for a subset of schools in southeast Michigan for the year 2000. The socioeconomic variables are obtained at the ZIP code level (where ZIP code is assigned to schools based on their mailing addresses).
Run the simple regression of math4 on pctsgle and report the results in the usual format. Interpret the slope coefficient. Does the effect of single parenthood seem large or small?
You intend to draw a random sample in order to test a hypothesis about an unknown population mean. You will use a hypothesis test. A description of each of the steps of a hypothesis test follows, but they may be specified in the incorrect order.
Specify the correct order of the steps:
-Draw a conclusion about the unknown population using what is known about the sample.
-Determine the null and alternative hypotheses.
-Select a sample and compute the z-score for the sample mean.
-Determine the probability at which you will conclude that the sample outcome is very unlikely.
Answers
The correct order of the steps in a hypothesis test are as follows:
Determine the null and alternative hypotheses.
Select a sample and compute the z-score for the sample mean.
Determine the probability at which you will conclude that the sample outcome is very unlikely.
Draw a conclusion about the unknown population using what is known about the sample.
First, you need to define the null and alternative hypotheses. The null hypothesis is the assumption that there is no significant difference between the sample and the population mean, while the alternative hypothesis is the opposite. Then, you need to select a random sample from the population and calculate the z-score for the sample mean. This involves finding the difference between the sample mean and the population mean, divided by the standard deviation of the sample mean.
Next, you need to determine the probability, known as the alpha level, at which you will conclude that the sample outcome is very unlikely, assuming that the null hypothesis is true. This is often set to 0.05 or 0.01. If the probability of obtaining the observed sample mean under the null hypothesis is lower than the alpha level, then the null hypothesis is rejected in favor of the alternative hypothesis.
Finally, you can draw a conclusion about the unknown population using what is known about the sample. If the null hypothesis is rejected, it suggests that there is a significant difference between the sample and the population mean, and the alternative hypothesis may be accepted.
Therefore, the correct order of the steps in a hypothesis test is to first determine the null and alternative hypotheses, then select a sample and calculate the z-score, determine the probability, and finally draw a conclusion based on the observed results.
To learn more about hypothesis test here:
brainly.com/question/30588452#
#SPJ11
A coin is tossed three times. An outcome is represented by a string of the sort HTT (meaning a head on the first toss, followed by two tails). The 8 outcomes are listed in the table below. Note that each outcome has the same probability. For each of the three events in the table, check the outcome(s) that are contained in the event. Then, in the last column, enter the probability of the event. Event A: A tail on the first toss or the second toss (or both) Event B: A head on each of the first two tosses Event C: Two or more tails THH HTH HTT Outcomes HHT 0 TTH THT HHH 0 TTT Probability П 0 0 00 믐 X Españe

Answers
SOLUTIONS
For each of the three events in the table, check the outcome(s) that are contained in the event. Then, in the last column, enter the probability of the event.
(a) Event A: A tail on the first toss or the second toss (or both)
\(\frac{P(TXX)orP(XTX)orP(TTX)}{possible\text{ outcome}}\)\(p(A\text{ tail on first or second or both\rparen=}\frac{6}{8}=\frac{3}{4}\)(b) Event B: A head on each of the first two tosses
\(\frac{P(HHX)}{possible\text{ outcome}}=\frac{2}{8}=\frac{1}{4}\)(c) Event C: Two or more tails
\(\frac{P(TTX)orP(XTT)orP(TXT)}{posible\text{ outcome}}\)\(P(two\text{ or more tails\rparen=4/8=1/2}\)
find the initial value seventeen years from now, Ms. speedis car, which is depreciating at 20% per year, will be worth $500
Answers
Answer:
Around 22200 dollars
Step-by-step explanation:
Firstly, it was depreciating 20% per year for 17 years. So, if we were to go back in time, it would be appreciating by 25%. Therefore, after doing the plugging in, it is 500 * 1.25^17. The initial value is around 22200. It is around 22204, to be exact.
A researcher tests the hypothesis that people who live in Florida spend less money on clothes than people who live in Pennsylvania because the weather is nicer. One hundred people who live in Florida and one hundred people who live in Pennsylvania are randomly selected and asked how much money they spend on clothes per year. In this study, what is the independent variable
Answers
The independent variable in this study is the place of residence, specifically whether the participants live in Florida or Pennsylvania.
The researcher is interested in examining the relationship between the location of residence and the amount of money spent on clothes. By selecting participants from both Florida and Pennsylvania, the researcher can compare the spending habits of individuals from these two locations and determine if there is a significant difference. Thus, the independent variable is the categorical variable that defines the groups being compared, which in this case is the place of residence.
Know more about place of residence here:
https://brainly.com/question/32383705
#SPJ11
I need help pls, what’s the answer?

Answers
Answer:
x₂ = - 3
Step-by-step explanation:
Calculate the slope m using the slope formula and equate to \(\frac{5}{6}\)
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (9, 9) and (x₂, y₂ ) = (x₂, - 1)
m = \(\frac{-1-9}{x_{2}-9 }\) , that is
\(\frac{-10}{x_{2}-9 }\) = \(\frac{5}{6}\) ( cross- multiply )
5(x₂ - 9) = - 60 ( divide both sides by 5 )
x₂ - 9 = - 12 ( add 9 to both sides )
x₂ = - 3
PLEASE HELP I REALLY NEED THIS ANSWERED, I NEED THE VOLUME OF BOTH CYLINDERS PLZ DONT USE AN ONLINE CALCULATOR THEY GIVE THE WRONG ANSWER

Answers
Answer:
\(\large\fbox{\green{\underline{Cylinder P :- \blue{ 794.0275 in ³}}}}\)
\(\large\fbox{\green{\underline{Cylinder Q :- \blue{1,307.81 in³}}}}\)
Step-by-step explanation:
Volume of cylinder = π × ( radius ) ² × h
1.) Here, radius = 4.25 in and height = 14 in.
Volume of cylinder = π × ( radius ) ² × height
substitute the values
Volume of cylinder P = 3.14 × ( 4.25 in ) ²×14 in.
now, simplify
= 3.14 × 18.0625 in²× 14 in.
= 3.14 × 252.875 in³
multiplying the value
= 794.0275 in³
\( \small \: \: \sf \: \fbox{ cirumference \: of \: cylinder \: P \: = {794.0275 in³}}\)
2.) Here, radius = 7 in. and height = 8.5 in.
Volume of cylinder Q = π × ( radius ) ² × height
substitute the values
Volume of cylinder Q = 3.14 × ( 7 in )² × 8.5 in.
Simplify
= 3.14 × 49 in² × 8.5 in.
multiply the values
= 3.14 × 416.5 in³
\( \small \sf \fbox{Volume of cylinder Q = 1,307.81 in ³}\)
A carpenter is making doors that are 2058 millimeters tall. If the doors are too long they must be trimmed, and if they are too short they cannot be used. A sample of 18 doors is made, and it is found that they have a mean of 2072 millimeters with a standard deviation of 33. Is there evidence at the 0.1 level that the doors are either too long or too short
Answers
The p-value is less than 0.1, so there is evidence at the 0.1 level that the doors are either too long or too short.
To determine if there is evidence that the doors are either too long or too short, we can conduct a hypothesis test.
Let's assume the null hypothesis (H0) is that the mean height of the doors is equal to 2058 millimeters, and the alternative hypothesis (Ha) is that the mean height of the doors is not equal to 2058 millimeters.
We can use a t-test to compare the sample mean of 2072 millimeters to the population mean of 2058 millimeters, given the sample size of 18 and the standard deviation of 33.
Calculating the test statistic using the formula:
t = (sample mean - population mean) / (standard deviation / sqrt(sample size))
Substituting the values:
t = (2072 - 2058) / (33 / sqrt(18))
Calculating the p-value associated with this test statistic, we find that it is less than 0.1.
Since the p-value is less than the significance level of 0.1, we reject the null hypothesis and conclude that there is evidence at the 0.1 level that the doors are either too long or too short.
Know more about p-value here:
https://brainly.com/question/33325466
#SPJ11
HELPPP ASAP PLEASE !!!!!

Answers
Answer:
the answer is 180°
Step-by-step explanation:
x+45°+55°+80°=360°
x+180=360°
x=360°-180°
x=180°
write the linear equation in standard form y=6x-4
Answers
Answer:
6x-y=4 is the answer.........
What is the measure of AngleY to the nearest whole degree?
Answers
Using the law of cosines, it is found that the measure of angle Y is of 64º.
What is the problem?The problem is incomplete, hence we research it on a search engine, and we have that we have a triangle in which:
The sides have lengths of 12, 16 and 17.The side of length 16 is opposite to angle Y.What is the law of cosines?The law of cosines states that we can find the side c of a triangle as follows:
c² = a² + b² - 2abcos(C)
In which:
C is the angle opposite to side c.a and b are the lengths of the other sides.For this problem, the parameters are given as follows:
a = 12, b = 17, c = 16, C = Y.
Hence:
c² = a² + b² - 2abcos(Y)
16² = 12² + 17² - 2(12)(17)cos(Y)
408cos(Y) = 177
cos(Y) = 177/408
Y = arccos(177/408)
Y = 64º.
The measure of angle Y is of 64º.
More can be learned about the law of cosines at https://brainly.com/question/4372174
#SPJ1
\(2(40 - 5y)=10y+5(1 - y)\)
Answers
Answer:
y = 5
Step-by-step explanation:
2(40 - 5y) : 80 - 10y
10y + 5(1 + y) : 5y + 5
80 - 10y = 5y +5
-10y = 5y -75
-10y - 5y = 5y - 75 - 5y
-15y/-15 = -75/-15
-15y/-15 : y
-75/-15 : 5
Hence, The answer should be 5
Evaluate the expression when b= 19 and c=5.
b+c²
b-3c
Simplify your answer as much as possible.
Answers
Answer:
b+\(c{2}\) = 19 + \(5^{2}\)
b-3c = 19 - 15
An ice skater skates completely around the two circles shown in the diagram. Each circle has a diameter of 20 meters. What is the approximate total distance skated by the ice skater? Use 3.14 for π . Round your answer to the nearest meter.
A) 628 meters
B) 251 meters
C) 126 meters
D) 63 meters
Answers
The solution is Option C.
The total distance skated by the ice skater is 126 meters
What is a Circle?
A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “centre”. Every line that passes through the circle forms the line of reflection symmetry. Also, the circle has rotational symmetry around the centre for every angle
The perimeter of circle = 2πr
The area of the circle = πr²
where r is the radius of the circle
Given data ,
Let the distance traveled by the skater be = D
Let the diameter of the circle A be = 20m
Let the diameter of the circle B be = 20m
So , the radius of circle A = 10 m
The radius of circle B = 10 m
Now , the value of π = 3.14
So , the distance traveled by the skater = perimeter of circle A + perimeter of circle B
Perimeter of Circle A = 2πr
Substituting the values in the equation , we get
Perimeter of Circle A = 2 x 3.14 x 10
Perimeter of Circle A = 62.8 m
And ,
Perimeter of Circle B = 2πr
Perimeter of Circle B = 2 x 3.14 x 10
Perimeter of Circle B = 62.8 m
Therefore , the distance traveled by the skater = Perimeter of Circle A + Perimeter of Circle B
Substituting the values in the equation , we get
The distance traveled by the skater = 2 x 62.8
The distance traveled by the skater = 125.6 meters
The distance traveled by the skater = 126 meters
Therefore , the value of D is 126 meters
Hence , The total distance skated by the ice skater is 126 meters
To learn more about circle click :
https://brainly.com/question/28391204
#SPJ2
someone please help.


Answers
The completed table with regards to terms of an expression are presented as follows;
Condition \({}\) (6·x + 3) + (5·x - 4) (-4·y - 16) - 8·y + 10 + 2·y
Exactly 3 terms N/A \({}\) N/A
Exactly 5 terms N/A \({}\) N/A
Includes a zero pair No \({}\) No
Uses distributive property No No
Includes a negative factor No
Has no like terms False False
Condition \(8 - \dfrac{1}{2} \cdot \left(4 \cdot x - \dfrac{1}{2} + 12\cdot x -\dfrac{1}{4} \right)\) 0.25·(8·m - 12) - 0.5·(-4·m + 2)
Exactly 3 terms No \({}\) No
Exactly 5 terms Yes \({}\) \({}\) No
Includes a zero pair No \({}\) \({}\) Yes
Uses the distributive property Yes \({}\) Yes
Includes a negative factor Yes \({}\) Yes
Has no like terms No \({}\) No
What is a mathematical expression?A mathematical expression is a collection of variables and numbers along with mathematical operators which are all properly arranged.
The details of the conditions in the question are as follows;
Terms of an expression
A term is a subunit of an algebraic expression which are joined together by operators such as addition or subtraction
Zero pair
A zero pair are two numbers that when added together have a zero result
Distributive property
The distributive property of multiplication states that the multiplication of a number or variable by an addend is equivalent to the sum of the multiplication of the number or variable and each member of the addend
Negative factor
A negative factor is a factor that has a negative sign prefix
Like terms
Like terms are terms consisting of identical variables with the same powers of the variable
Learn more about expressions here:
https://brainly.com/question/1859113
#SPJ1
find the value of x in the proportion.
18/x = 9/7
Answers
Here you go
Hope this helps you
Noncollinear points are points that do not lie on the
same line.
A.
Undefined
Terms
B.
Defined
Terms
C.
Postulates
D.
Theorems
Answers
Noncollinear points are points that do not lie on the same line as defined terms.
What do you mean by defined terms?
Defined terms are words that are given a specific definition in a contract. The term's definition applies in the context of the particular contract and the definitions are usually only applicable to that contract.
If you see a capitalized word in a contract, the chances are its definition is somewhere in the document.
Defined terms give clarity and a sense of definitiveness to a contract.
They also remove ambiguity and make contracts easier to understand.
Collinear points are two or more straight-line points, whereas non-collinear points are points that do not lie on a single straight line.
Learn more about defined terms here:
https://brainly.com/question/4258163
#SPJ1
a flashlight battery manufacturer makes a model of battery whose mean shelf life is three years and four months, with a standard deviation of three months. the distribution is approximately normal. one production run of batteries in the factory was 25,000 batteries. how many of those batteries can be expected to last between three years and one month and three years and seven months?the is the average value of a set of numerical data, found by adding all the values and dividing by the number of elements in the set.
Answers
The number of batteries expected to last between three years and one month and three years and seven months, is 12,500 batteries.
Given that the mean shelf life of the flashlight batteries is three years and four months and the standard deviation is three months.
To find the number of batteries that can be expected to last between three years and one month (3.08 years) and three years and seven months (3.58 years), we need to calculate the probability within this range.
First, we convert the given time intervals to years:
Three years and one month = 3.08 years
Three years and seven months = 3.58 years
Next, we calculate the z-scores for these values using the formula:
z = (x - μ) / σ
For 3.08 years:
z1 = (3.08 - 3.33) / 0.25 = -1
For 3.58 years:
z2 = (3.58 - 3.33) / 0.25 = 1
Now, we can use the standard normal distribution table or a calculator to find the probabilities corresponding to these z-scores.
The probability of a value falling between -1 and 1 is the difference between the two probabilities.
Let's assume that the distribution is symmetric, so half of the batteries would fall within this range.
Therefore, the number of batteries that can be expected to last between three years and one month and three years and seven months is approximately:
Number of batteries = 0.5 × Total number of batteries = 0.5 × 25,000 = 12,500 batteries.
Learn more about Standard Deviation here:
https://brainly.com/question/475676
#SPJ11
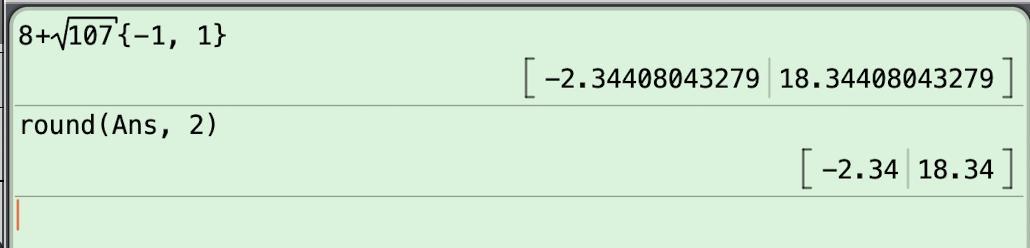
Please help! This is part of my grade, please make sure to read the question before answering because I need this to be correct (35 points)

Answers
Answer:
u = -2.34 or u = 18.34
Step-by-step explanation:
You want to solve u² -16u = 43 by completing the square.
Completing the squareTo complete the square, add the square of half the coefficient of the linear term to both sides.
u² -16u +(-16/2)² = 43 +(-16/2)²
u² -16u +64 = 107 . . . . . . . simplify
(u -8)² = 107 . . . . . . . . . write as a square
u -8 = ±√107 . . . . . . square root
u = 8 ± √107 . . . add 8
u = -2.34 or u = 18.34 . . . . . find the decimal values
<95141404393>
Write the equation for each table

Answers
Answer:
Step-by-step explanation:
First table:(left)
(1, 15) (2, 30)
(30 - 15)/(2 - 1) = 15/1 = 15
y - 15 = 15(x - 1)
y - 15 = 15x - 15
y = 15x
Second table:(right)
(0, 10) (1, 25)
(25 - 10)/(1 - 0)= 15/1= 15
y - 10 = 15(x - 0)
y - 10 = 15x - 0
y = 15x + 10
the diagram gives the dimensions of a swimming pool, what will be the approximate area of the cover

Answers
Answer:
Step-by-step explanation:
if we wouldnt have the semicircle, all would be easy...
Area , A=10*30=300 ft^2
the semicircle has a diameter d=12 ft, than r=6
Area of the circle is Ac=3.14*r^2=113.10 ft^2
we need half of that
113.10/2=56.55
the area of the cover would be
300-56.55=243.45 ft^2
Cuál es el menor número entero que, disminuido en 8, resulta menor que su triple
Answers
Answer:
-3
Step-by-step explanation:
Let x = the number
Then 3x = its triple, and the condition is:
x - 8 < 3x
Subtract x from each side
-8 < 2x
Divide each side by 2
-4 < x
Reverse the inequality
x > -4
The smallest integer greater than -4 is -3.
Check:
-3 - 8 < 3(-3)
-11 < -9
It checks.
a person leaves home at 8:00 am and drives to a destination at a rate of 40 miles per hour. the person returns at a rate of 25 miles per hour and arrives at 2:30 pm. how far was the destination?
Answers
Answer:
100mi
Step-by-step explanation:
Suppose that there are no restrictions on how many pages a printer can print. How many ways are there for the 100 pages to be assigned to the four printers
Answers
There are 176,851 ways to assign the 100 pages to the four printers.
Since there are no restrictions on how many pages a printer can print, we can think of this problem as distributing 100 identical pages among 4 distinct printers. This is an example of a "balls and urns" problem, which can be solved using the stars and bars formula.
The stars and bars formula states that the number of ways to distribute k identical objects among n distinct containers is:
C(k+n-1, n-1)
where C represents the combination function. In this case, we have k = 100 identical pages and n = 4 distinct printers. Therefore, the number of ways to assign the pages to the printers is:
C(100+4-1, 4-1) = C(103, 3) = 176,851
So there are 176,851 ways to assign the 100 pages to the four printers.
To learn more about statistics here
https://brainly.com/question/15525560
#SPJ4
You need 3 sticks of butter for every 24cookies you bake.
Complete the table using equivalent ratios.
Sticks of butter Number of cookies
3 24
?
16 ?
5 ?
Answers
The table formed using equivalent ratios.
16 : 128
5 : 40.
Explain the term equivalent ratios?When we compare two ratios, they are said to be equivalent. To determine whether two or more ratios are equivalent, they can be compared to one another. For instance, 1:2 and 2:4 have the same ratio.3 sticks of butter -----> 24 cookies.
Let the number of cookies made for other stick of butter be 'y'.
Then, number cookies for the 16 sticks of butter
3/24 = 16/ y
y = 16*24 / 3
y = 128 cookies.
Again, number cookies for the 5 sticks of butter
3/24 = 5/ y
y = 5*24 / 3
y = 40 cookies.
Thus, number of cookies made by 5 sticks of buter are 40.
To know more about the equivalent ratios, here
https://brainly.com/question/2914376
#SPJ4
Two hikers start a trip from a camp walking 15 miles due east. They turn north and walk 17 miles to a large pond. How far is the pond from base camp to the nearest tenth of a miles.
Answers
Answer:
22.7 miles
Step-by-step explanation:
The hikers start walking 15 miles due east and then they turn north and walk 17 miles to a large pond.
The shape of their journey can be represented as a right angled triangle, shown below.
To find the distance between the pond and the base camp, we need to find the hypotenuse of the triangle.
We can do this by using Pythagoras theorem:
\(hyp^2 = a^2 + b^2\)
where a and b are the other two sides of the triangle. Therefore:
\(hyp^2 = 15^2 + 17^2\\\\hyp^2 = 514\\\\hyp = \sqrt{5`4} \\\\hyp = 22.7 miles\)
The pond is 22.7 miles far from the base camp.

solve the equations below exactly. Give your answers in radians, and find all possible values for t in the interval 0 < t < 2pi. enter your solutions in a comma separated list.

Answers
To find each answer, we just have to solve for t. It is important to use the important angles in trigonometry to provide an exact answer.
\(\begin{gathered} \sin t=-\frac{\sqrt[]{2}}{2} \\ t=\sin ^{-1}(-\frac{\sqrt[]{2}}{2})=225 \end{gathered}\)The first answer is t = 225°.
\(\begin{gathered} \cos t=\frac{\sqrt[]{3}}{2} \\ t=\cos ^{-1}(\frac{\sqrt[]{3}}{2}) \\ t=30 \end{gathered}\)The second answer is 30°.
\(\begin{gathered} \tan t=-\frac{1}{\sqrt[]{3}} \\ t=\tan ^{-1}(-\frac{1}{\sqrt[]{3}}) \\ t=150 \end{gathered}\)The third answer is t = 150°.