A new phone was originally $200. It was on sale for 10% off the original price. When Carmen bought
the phone, she use a coupon for an additional 30% off the sale price. What was the overall percent discount
from the original price of the phone to the price that Carmen paid?
Answers
If looking for the number of the price of the phone with the discounts it’s 80
Related Questions
Integrate the given function over the given surface. G(x,y,z) = x over the parabolic cylinder y = x2, 0sxs v2, 0szs2 Integrate the function. 556(x,y,z) do = 0 (Type an integer or a simplified fraction.)
Answers
To integrate the function G(x, y, z) = x over the parabolic cylinder defined by y = x^2, 0 ≤ x ≤ √2, and 0 ≤ z ≤ 2, we need to set up a triple integral over the specified region.
The integral is given by:
∫∫∫ G(x, y, z) dV
We can express the integral in terms of x, y, and z as follows:
∫∫∫ x dV
To evaluate this integral, we need to express the differential volume element dV in terms of x, y, and z. In this case, since we are integrating over a cylindrical region, we can express dV as dA dz, where dA represents the differential area element in the xy-plane.
The equation of the parabolic cylinder is y = x^2. To express the differential area element dA, we can use the Jacobian of the transformation from Cartesian coordinates (x, y, z) to cylindrical coordinates (r, θ, z).
The Jacobian determinant is |J| = r, where r is the radial distance in the xy-plane.
Thus, dA = r dr dθ. However, since we are only interested in the region where 0 ≤ x ≤ √2, the limits of integration for r and θ will be determined by the given range of x.
For the given region, we have the following limits of integration:
0 ≤ x ≤ √2
0 ≤ z ≤ 2
To convert the function G(x, y, z) = x to cylindrical coordinates, we need to express x in terms of r and θ. In this case, x = r cos(θ).
Now we can rewrite the integral using cylindrical coordinates:
∫∫∫ x dV = ∫∫∫ (r cos(θ))(r dr dθ dz)
The limits of integration become:
0 ≤ r ≤ √2
0 ≤ θ ≤ 2π
0 ≤ z ≤ 2
We can now evaluate the integral:
∫∫∫ (r^2 cos(θ)) dr dθ dz
Integrating with respect to r first, we have:
∫∫ (r^3/3 cos(θ)) |r=0 to r=√2 dθ dz
Simplifying:
∫∫ (√2^3/3 cos(θ)) dθ dz
∫∫ (2√2/3 cos(θ)) dθ dz
Now integrating with respect to θ:
∫ (2√2/3 sin(θ)) |θ=0 to θ=2π dz
∫ (2√2/3)(0 - 0) dz
∫ 0 dz = 0
Therefore, the value of the integral ∫∫∫ G(x, y, z) dV over the given parabolic cylinder is 0.
To know more about parabolic refer here
https://brainly.com/question/14003217#
#SPJ11
Why is it that people are fake? Need answer ASAP will mark brainlist
Answers
Answer:
They feel like they are superior to you, and think that you won't find out that they are bein fake.
Step-by-step explanation:
It's either that or they just want people to like them, so they become fake in order to fit into society.
The equation that can be used to determine how much danil has spent is 3 x 32 25 . Part 2 how much did danil spent $
Answers
The equation that gives how much Daniel has spent is:
y = 2x - 26.
The amount spent by Daniel is of: $20.
What is the system of equations?The variables of the system of equations are given as follows:
Variable x: Amount spent by Daniel.Variable y: Amount spent by Jaclyn.Jaclyn spent $26 less than 2 times what Daniel spent, hence the equation is:
y = 2x - 26.
The amount spent by Jaclyn is given in the problem as follows:
y = 14.
Hence the amount spent by Daniel is found replacing the amount spent by Jaclyn on the first equation as follows:
14 = 2x - 26
2x = 40
x = 40/2
x = 20.
Missing InformationThe problem is:
While shopping for clothes, Jaclyn spent $26 less than 2 times what Daniel spent. Jaclyn spent $14.
More can be learned about a system of equations at https://brainly.com/question/24342899
#SPJ1
Sophia borrowed $945 from a bank at a rate of 7.25% for 48 months. How much money is in her account after 48 months?
Answers
Step-by-step explanation
Ok so, use the formula I=Prt
Meaning principal, rate, and time.
First, turn the % into 100...
Or just move the decimal two times to the right.
= .0725
Next, turn 48 months into years. 12 ÷ 4 = 48.
= 4 years
And finally, multiply ♀
You can multiple them in the order of the formula.
945× 0.0725 × 4
Giving you the answer of, $274.05.
Hopefully this helps ♀
hopefully this can help you
what is the measurement of the missing angle

Answers
Answer:
88
Step-by-step explanation:
A straight line has 180 degrees so you would subtract 92 from 180 which gives you 88.
Answer: The answer is 88 degrees
Step-by-step explanation:
A straight line is 180 degrees by default, so just subtract the known angle from 180 (180-92=88)
The function f(x)=4∙2^x is graphed to the right. Sketch a graph of the function g(x) represented by the rule g(x)=f(x-2)+3. Mark the asymptote to help make your graph clear.


Answers
Given:
\(f(x)=4\cdot2^x\)The rule for function g(x) is,
\(g(x)=f(x-2)+3\)The function becomes,
\(\begin{gathered} f(x)=4\cdot2^x \\ f(x-2)=4\cdot2^{x-2}=4\cdot\frac{2^x}{2^2}=2^x \\ f(x-2)+3=2^x+3 \end{gathered}\)Therefore,
\(g(x)=f(x-2)+3=2^x+3\)The graph of the function g(x) is,

A recent study reported that 60% of the children in a particular community were overwoight or obese. Suppose a random sample of 200 public school children is taken from this community. Assume the sample was taken in such a way that the conditions for using the Central Limit Theorem are met. We are interested in finding the probability that the proportion of overveightfobese children in the sample will be greater than 0.57. Complete parts (a) and (b) below. a. Before doing any calculations, determine whether this probability is greater than 50% or less than 50%. Why? A. The answer should be less than 50%. because 0.57 is less than the population proportion of 0.60 and because the sampling distribution is approximately Normal. B. The answer should be greater than 50%, because the resulting z-score will be positive and the sampling distribution is approximately Normal. C. The answer should be greater than 50%, because 0.57 is less than the population proportion of 0.60 and because the sampling distribution is approximately Normal. 0. The answer should be less than 50%, because the resulting z-score will be negative and the sampling distribution is approximately Normal.
Answers
The probability that the proportion of overweight or obese children in the sample will be greater than 0.57 is less than 50%.
The first paragraph summarizes the answer, stating that the probability is less than 50% because 0.57 is less than the population proportion of 0.60, and the sampling distribution is approximately normal.
In the second paragraph, we can explain the reasoning behind this conclusion. The Central Limit Theorem states that for a large sample size, the sampling distribution of the sample proportion will be approximately normal, regardless of the shape of the population distribution. In this case, the sample was taken in a way that meets the conditions for using the Central Limit Theorem.
Since the population proportion of overweight or obese children is 0.60, any sample proportion below this value is more likely to occur. Therefore, the probability of obtaining a sample proportion greater than 0.57 would be less than 50%. This is because the resulting z-score, which measures how many standard deviations the sample proportion is away from the population proportion, would be negative.
To summarize, the probability of the proportion of overweight or obese children in the sample being greater than 0.57 is less than 50% because 0.57 is less than the population proportion of 0.60, and the sampling distribution is approximately normal.
To learn more about probability click here, brainly.com/question/31828911
#SPJ11
Which best describes the triangle?

Answers
Answer: acute and isosceles
Step-by-step explanation: Notice that the triangle shown here has no right angles and no obtuse angles, which means that all of the angles of the triangle are acute. When classifying triangles, if all of the angles of the triangle are acute, then the triangle is acute.
Now, notice that two sides of the triangle have the same length.
If two sides of a triangle have the same length,
then we say that the triangle is isosceles.
So this triangle is acute and isosceles.
Find the values of the variables!
Please help! I’ll give brainliest to the first person :)))
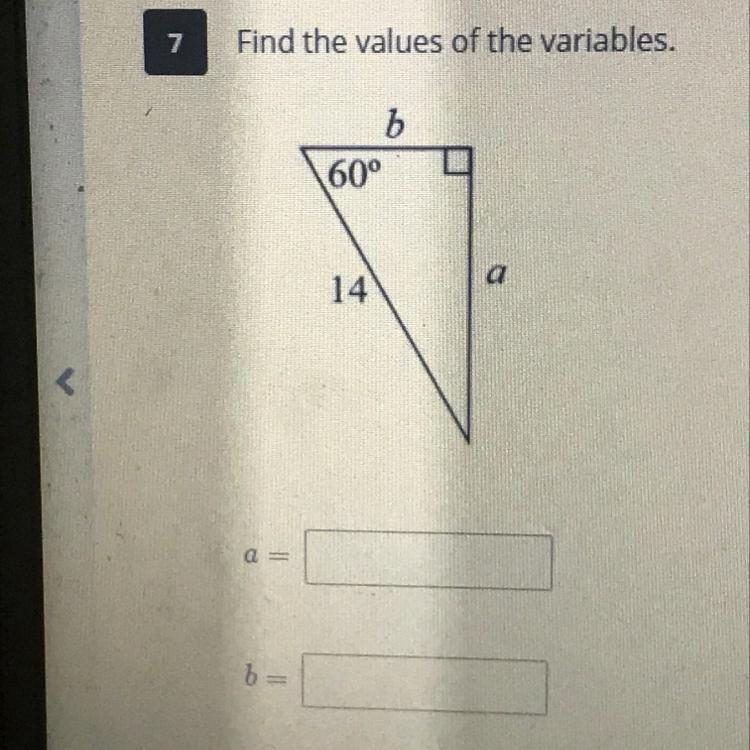
Answers
Answer:
b = 7 and a = 7\(\sqrt{3}\)
Step-by-step explanation:
This is because the angle across from 90 degrees equals 14. and this is a 30 - 60 - 90 triangle. therefore the unknown angle is 30 degrees. Which makes b half of the hypotenuse, or 14, so it becomes 7. and the side opposite to 60 degrees is root 3 times whatever b is. so a becomes 7 root 3. Hope this helps.
Give g(x)=2x+3, find g(-3)
Answers
Answer:
2
Step-by-step explanation:
g(x)=2x+3
La derivada de un polinomio es la suma de las derivadas de sus términos. La derivada de cualquier término constante es 0. La derivada de ax
n
es nax
n−1
.
2x
1−1
Resta 1 de 1.
2x
0
Para cualquier término t excepto 0, t
0
=1.
2×1
Para cualquier término t, t×1=t y 1t=t.
2
2. A recipe calls for 3 and 1/2 cups of flour and 3/4 cups of sugar, If you want
to make the recipe with 6 cups of flour, how much sugar will you need? *
Answers
Answer:
1 and 2/7 cups of sugar.
Step-by-step explanation:
The ratio of the amount of flour in the original recipe to the amount in your recipe is 1:12/7. (6 / 7/2 = 6 * 2/7 = 12/7)
Therefore, the amount of sugar you need can be found by 3/4 * 12/7 = 36/28 = 9/7 cups of sugar, which equates to 1 and 2/7 cups.
Hope this helped!
The right set of parallel lines is a translation right 10 units of the left set of
parallel lines. Drag the left set of parallel lines and try to move them onto the right set. Are the two sets of parallel lines the
same? What does this mean about how parallel lines change when you translate them?
Answers
The translation of angles and parallel lines is discussed in the following query. Below is a detailed response.
When you translate an item in geometry, you are essentially turning it in a different direction. Consequently, an angle that has been translated is one that has been turned in a new direction.
The photograph from the first selection in section A makes it obvious that the angle remained the same. From the positive to the negative side of the x-axis, it moves seven units.
The angles also don't alter from Part B. It should be noted that a translation or rotation of an angle has no effect on the angles.
What we got is the reflection of the angles from Part C. Due to the fact that they are reflections of one another, this indicates that both angles are equal.
The two parallel sets of lines from Part D will continue to be parallel as long as they are both translated at the same time.
The parallel line that is at an angle to the Y-axis will not meet the parallel line that is at an angle to the x-axis if they are extended infinitely, despite the fact that in each set of parallel lines, the two sets of lines remain equally distant from one another.
To learn more about Angle Translation, here:
brainly.com/question/13066649
#SPJ1
Your question is incomplete but most probably your full question was,

Shen made $115 for 5 hours of work.
At the same rate, how many hours would he have to work to make $207?
Answers
Answer:
It would take Shen 8.99999999802 hours to make $207.
Step-by-step explanation:
5/115 = 0.04347826086
207 x 0.04347826086 = 8.99999999802
You start with $19 in cash. After you buy a pair of jeans for $17 find $10 while walking and buy a $2 soda how much cash would you have left?
Answers
Answer:
10
Step-by-step explanation:
19-17=2
10+2=12-2 =10
8 - ( 3 + b ) = b - 9
b = ?
Answers
Answer:
b = 7
Step-by-step explanation:
8 - 3 - b = b - 9
5 - b = b - 9
2b = 14
b = 7
Answer:
b=7
Step-by-step explanation:
isolate the variable by dividing each side by factors that don't contain the variable.
\( \sqrt{28} \)simplest radical form
Answers
Recall following property of radicals:
\(\sqrt[]{a\cdot b}=\sqrt[]{a}\cdot\sqrt[]{b}\)Since 28 can be factorized as:
\(2^2\cdot7\)Use the property previoulsy mentioned to rewrite the square root of 28:
\(\begin{gathered} \sqrt[]{28}=\sqrt[]{2^2\cdot7} \\ =\sqrt[]{2^2}\cdot\sqrt[]{7} \\ =2\cdot\sqrt[]{7} \end{gathered}\)Therefore, the simplest radical form of the square root of 28, is:
\(2\cdot\sqrt[]{7}\)How tall is a building that casts a 20 foot shadow if the angle of elevation from the ground to the top of the building is 43∘ ?
Answers
To determine the height of the building, we can use trigonometry. In this case, we can use the tangent function, which relates the angle of elevation to the height and shadow of the object.
The tangent of an angle is equal to the ratio of the opposite side to the adjacent side. In this scenario:
tan(angle of elevation) = height of building / shadow length
We are given the angle of elevation (43 degrees) and the length of the shadow (20 feet). Let's substitute these values into the equation:
tan(43 degrees) = height of building / 20 feet
To find the height of the building, we need to isolate it on one side of the equation. We can do this by multiplying both sides of the equation by 20 feet:
20 feet * tan(43 degrees) = height of building
Now we can calculate the height of the building using a calculator:
Height of building = 20 feet * tan(43 degrees) ≈ 20 feet * 0.9205 ≈ 18.41 feet
Therefore, the height of the building that casts a 20-foot shadow with an angle of elevation of 43 degrees is approximately 18.41 feet.
Learn more about probability here
brainly.com/question/13604758
#SPJ11
Answer both parts complete correct and super fast to get thumbs up and a good comment!!
Part A:
To find:
1) Variable cost
2) Average cost
3) Fixed cost
Data:
Units = 25 units/hour
Fixed cost per unit = 15.25$
Labor cost per hour = 12$ per person
Required labor per hour = 10
Material cost = 0.075$ per unit
Part B:
One client requested 15 additional uniter per hour and willing to pay 10$ per unit for the remaining units. Determine the marginal cost?
Answers
To calculate the variable cost, average cost, and fixed cost, we can use the given data. The variable cost per unit is $9.375, the average cost per unit is $24.625, and the fixed cost is $253.75.
Variable cost:
The variable cost includes the labor cost and material cost.
Labor cost per hour = $12
Required labor per hour = 10 units
Labor cost per unit = $12 / 10 = $1.2
Material cost per unit = $0.075
Variable cost per unit = Labor cost per unit + Material cost per unit
Variable cost per unit = $1.2 + $0.075 = $1.275
Average cost:
Average cost is the total cost divided by the number of units produced.
Total cost = Fixed cost + Variable cost
Fixed cost = $15.25
Variable cost per unit = $1.275
Average cost per unit = Total cost / Units
Average cost per unit = ($15.25 + $1.275) / 25
Average cost per unit = $16.525 / 25 = $0.661
Fixed cost:
Fixed cost is the cost that does not change with the level of production.
Fixed cost = Fixed cost per unit * Units
Fixed cost = $15.25 * 25 = $253.75
Part B:
To determine the marginal cost for the additional units requested by the client, we need to calculate the additional variable cost. The marginal cost per unit is $10.
The client requested an additional 15 units per hour and is willing to pay $10 per unit for the remaining units.
Additional variable cost per unit = Material cost per unit
Additional variable cost per unit = $0.075
Therefore, the marginal cost per unit for the additional units requested by the client is $10.
Learn more about marginal cost: brainly.com/question/17230008
#SPJ11
compare adding and subtracting to multiplying and dividing bases with different exponents.
Answers
Exponent rules for addition and subtraction are identical to one another. As a reminder, all terms' bases must be the same in order to remove terms with exponents. All terms' exponents must be equal.
Define exponents.A number written as a superscript over another number is known as an exponent. In other words, it means that the base has been elevated to a particular level of power. Other names for the exponent are index and power. mn indicates that m has been multiplied by itself n times if m is a positive number and n is its exponent.
Given,
Adding and subtracting to multiplying and dividing bases with different exponents.
Exponent rules for addition and subtraction are identical to one another. As a reminder, all terms' bases must be the same in order to remove terms with exponents. All terms' exponents must be equal.
The exponents and variables must match in order to add exponents. The exponents are left constant while the variable coefficients are added. The addition only includes terms with the same variables and powers. Exponents can be multiplied and divided according to this rule.
To learn more about exponents, visit:
https://brainly.com/question/5497425
#SPJ1
(x−119)÷7=6
Could anyone please help?
Answers
Answer:
x
=
161
Step-by-step explanation:
Multiply both sides of the equation by
7
.
7
⋅
(
x
−
119
)
÷
7
=
7
⋅
6
Simplify both sides of the equation.
Tap for more steps...
x
−
119
=
42
Move all terms not containing
x
to the right side of the equation.
Answer:
161
Step-by-step explanation:
Step 1:
( x - 119 ) ÷ 7 = 6 Equation
Step 2:
( x - 119 ) = 42 Multiply 7 on both sides
Step 3:
x = 42 + 119 Add 119 on both sides
Answer:
x = 161 Add
Hope This Helps :)
Consider the problem outlined in class: Can a 6-month exercise program increase the total body bone mineral content (TBBMC) of young women? Assume that o = 2 for the percent change in TBBMC over the 6-month period and the investigators aim to recruit 50 subjects. If a power of 80% is desired with an a =0.05, what is the minimum effect size (given by a percent change in TBBMC), that this sample size can observe? Round to 4 decimal places for the answer.
Answers
The minimum effect size that this sample size of 50 can observe is approximately 0.6966
To calculate the minimum effect size that the given sample size can observe, we need to use the concept of statistical power.
The power of a statistical test represents the probability of correctly rejecting the null hypothesis when the alternative hypothesis is true. In this case, the alternative hypothesis would be that the 6-month exercise program has a significant effect on the total body bone mineral content (TBBMC) of young women.
Sample size (n) = 50
Standard deviation (σ) = 2 (percent change in TBBMC)
Desired power = 80%
Significance level (α) = 0.05 (Type I error rate)
To calculate the minimum effect size, we can use a power analysis formula. In this case, we'll use the formula for a t-test:
Effect size (d) = (M1 - M2) / σ
where M1 and M2 are the means of the two groups being compared (in this case, the TBBMC before and after the exercise program).
Since we want to find the minimum effect size, we need to rearrange the formula:
(M1 - M2) = d * σ
Now, let's calculate the minimum effect size using the desired power and other given values:
Using statistical software or tables, we can find that the critical value for a one-tailed t-test with α = 0.05 and degrees of freedom (df) = n - 1 is approximately 1.676.
The formula for calculating power is:
Power = 1 - β
where β is the Type II error rate.
Given that power = 0.8, we can calculate β:
β = 1 - Power
β = 1 - 0.8
β = 0.2
Using the critical value and β, we can calculate the non-centrality parameter (δ) for the t-test:
δ = critical value - (β / √n)
δ = 1.676 - (0.2 / √50)
δ = 1.676 - 0.2828
δ = 1.3932
Finally, we can calculate the minimum effect size (d) using the formula:
d = δ / σ
d = 1.3932 / 2
d = 0.6966
To know more about sample size click here
brainly.com/question/31734526
#SPJ11
geometry: follow directions below for each figure. Show steps. Circle answers. find the area of each figure.
HELP ASAP!!
THANKS IF YOU DID!!

Answers
Answer:
A = 5.6 m^2
Step-by-step explanation:
The area of a trapezoid is given by
A = 1/2 h( b1+b2) where h is the height and b1 and b2 are the lengths of the bases
A = 1/2 (2) (4+1.6)
A = 1(5.6)
A =5.6 m^2
Answer:
Step-by-step explanation:
b1 = 4 m ; b2= 1.6m ; h = 2m
\(A =\frac{1}{2}h(b_{1}+b_{2})\\\\=\frac{1}{2}*2(4+1.6)\\\\=\frac{1}{2}*2*5.6\\\\=5.6 m^{2}\)
How many elementary events are in the sample space of the experiment of rolling three fair coins? O2 09 O 8 6
Answers
Melanie is looking for a loan. She is willing to pay no more than an effective rate of 9. 955% annually. Which, if any, of the following loans meet Melanie’s criteria? Loan A: 9. 265% nominal rate, compounded weekly Loan B: 9. 442% nominal rate, compounded monthly Loan C: 9. 719% nominal rate, compounded quarterly a. B only b. A and C c. A and B d. None of these fit Melanie’s criteria. Please select the best answer from the choices provided A B C D.
Answers
Melanie should take A and B, being r(loan a)= 9.699% annually, r(loan b)=9.862% annual
What options Melanie should choose for the best deal?It is given that
Loan A: 9.265% nominal rate, compounded weekly
In order to find the easiest effective rate, we need to divide this rate by 52 (which are the weeks in a year). Once we do that, we convert this effective weekly rate into an effective annual rate. Let´s walk you through all this.
\(r(Eweek)=\dfrac{0.09265}{52} =0.00178173\)
Or 0.178173% effective weekly. Now we can transform it into an effective annual rate.
\(r(e,a)=1+(r(e.week))^{52} -1\)
\(r(e,a)=1+(0.00178173)^{52} -1=0.09699\)
Or 9.669% annual, which is less than 9.955%, so this one is selected, let´s check the next.
Loan B: 9.442% nominal rate, compounded monthly
Just like we did with Loan A, we need to divide this rate too, only this time, we will divide by 12, therefore obtaining an effective monthly rate.
\(r(Emonth)=\dfrac{0.09442}{12} =0.00786833\)
Or 0.786833% effective monthly, let´s turn it into an effective annual rate.
\(r(e,a)=1+(r(e.month))^{12} -1\)
\(r(e,a)=1+(0.00786833))^{12} -1=0.09862\)
Or 9.862% annual, so this rate would work for Melanie too. This means that option C) is the answer we are looking for but, let´s walk that extra mile and turn that Loan C rate into an annual rate.
\(r(Eweek)=\dfrac{0.09719}{4} =0.0242975\)
or 2.42975% effective quarterly, now, let´s convert it into an effective annual rate.
\(r(e,a)=1+(0.0 242975))^{12} -1=0.010079\)
That is 10.079% effective annual, therefore, Loan C is not an option for Melanie.
Thus Melanie should take A and B, being r(loan a)= 9.699% annually, r(loan b)=9.862% annual
To know more about Compound interest follow
https://brainly.com/question/24924853
Michelle is scuba diving. Her position changes from −2. 1 m to -38. 6 in 6 1/4 min. What is the average change in Michelle’s position each minute?
Answers
To find the average change in Michelle's position each minute, we need to calculate the total change in her position and divide it by the total time elapsed.
The initial position is -2.1 m and the final position is -38.6 m, resulting in a total change of: Total change = Final position - Initial position = -38.6 m - (-2.1 m) = -38.6 m + 2.1 m = -36.5 m. The time elapsed is 6 1/4 minutes, which can be expressed as a mixed fraction or an improper fraction: Time elapsed = 6 1/4 minutes = 25/4 minutes. Now, we can calculate the average change in position per minute: Average change per minute = Total change / Time elapsed= (-36.5 m) / (25/4 min) = (-36.5 m) * (4/25 min) ≈ -5.84 m.
Therefore, the average change in Michelle's position each minute is approximately -5.84 meters.
To learn more about average click here: brainly.com/question/897199
#SPJ11
plzzzzzz hellppppp it is for mathh

Answers
Answer:
3^4 (3rd option)
:)
Answer:
the answer is optionc) 3 is to power 4 because
3 is to power 4 mean to multiply the whole number 3 itself 4 time which is 81,greater than 4ia to power 4
example
4 Is to power3=4×4×4=64
7 is to power 2 =49
5is to power 2=25
3 is to power 4 =81
2 is to power 5=32
therefore option c is greater than 4 is to power 3
una persona olvido su paraguas en un autobuses pero se acordó que la suma de los digitos del l camion eran 11 si su producto son 24 que numeros eran del camion
Answers
Ecuaciones
Llamemos x al primer número del camión y y al segundo número.
Tenemos que su suma es 11, así que:
x+y=11
También sabemos que su producto es 24:
xy=24
De esta forma, tenemos un sistema de ecuaciones. Vamos a despejar la x de la primera ecuación:
x=11-y
Y la reemplazamos en la segunda:
(11-y)y=24
Operamos y ordenamos el poninomio para formar la ecuación cuadrática:
\(\begin{gathered} 11y-y^2=24 \\ y^2-11y+24=0 \end{gathered}\)Para hallar las soluciones de esta ecuación, tomemos los coeficientes de la ecuación de segundo grado:
a=1, b=-11, c=24
Y aplicamos la fórmula resolvente
\(\begin{gathered} y=\frac{-\text{b}\pm\sqrt[]{b^2-4ac}\text{ }}{2a} \\ y=\frac{11\pm\sqrt[]{(-11)^2-4(1)(24)}\text{ }}{2(1)} \\ y=\frac{11\pm\sqrt[]{121-96}\text{ }}{2} \\ y=\frac{11\pm\sqrt[]{25}\text{ }}{2} \\ y=\frac{11\pm5\text{ }}{2} \end{gathered}\)Tenemos dos posibles respuetas:
y=16/2=8
y=6/2=3
Sustituimos ambas respuestas para hallar x:
x=11-y
x=11-8=3
x=11-3=8
En cualquier orden que los tomemos, los números del camón eran 3 y 8
in an experiment a group of participants who are not exp[osed to the independent variables are known as
Answers
The group of participants who are not exposed to the independent variables are the known as the control group.
Good luck! :)
What is the following sum?

Answers
Answer:
i think its c
Step-by-step explanation:
Timothy periodically purchases bonds issued by prince waste collection. last year, he bought two bonds in february, two bonds in june, and one bond in august, then sold them all in october. prince waste collection bonds were selling at 94.593 in february, 92.661 in june, 105.480 in august, and 102.882 in october. if each bond that timothy bought had a par value of $1,000, how much profit did he make from buying and selling these bonds? a. $15.91 b. $34.42 c. $159.12 d. $344.22
Answers
The profit Timothy made from buying and selling the bonds is =
b. $34.42
What do you mean by profit and loss?A person either gains money or loses money when they purchase something for one price and then sell it for another. There are many terminologies used in connection with the complete transaction procedure.
Take the cost price (C.P.), selling price (S.P.), discount, marking price, profit, and loss as examples.
Now, as per the question:
Total amount spent for the bonds in the month of February =
2 × $94.593 = $189.186
Total amount spent for the bonds in the month of June =
2 × $92.661 = $185.322
Total amount spent for the bonds in the month of August =
1 × $105.480 = $105.480
Now total amount he received after selling the bonds in the month of October = 5 × $102.882 = $514.410
So, the total profit made = $514.410 - ($189.186+$185.322+$105.480)
⇒ Profit = $34.422.
To know more about profit and loss, visit:
https://brainly.com/question/12634106
#SPJ1