a carpenter has a wooden dowel that is 96 cm long. she wants to cut it into two pieces so that one piece is 5 times as long as the other. what is the length of the longer piece?
Answers
Answer:
30 cmStep-by-step explanation:
In this problem (word problem), we are examined on how to express equations from words.
let us initialize some variables
let the length of the first piece (the short piece) be x
and that of the second(the longer piece) be 5x
given that the total length is 96 cm
Also from the problem statement, the total length can be expressed as
5x+x= 96
6x= 96
divide both sides by 6 to solve for x
x= 96/6
x= 16
now the longer side = 5x
the longer side= 5*6
the longer side = 30 cm
Related Questions
Mike owes his friends $7  he got his weekly allowance of $20 paid back his friend and downloaded a nine dollar album how much money does he have left
Answers
13-9=4
He has $4 left
How many factors does100 have in all?
Answers
Answer:
Total of 9 factors
Step-by-step explanation:
1, 2, 4, 5, 10, 20, 25, 50, 100
1x100=100
2x50=100
4x25=100
5x20=100
Cards numbered 500 through 799 are placed into a box. How many of the cards satisfy both of the conditions shown below?
The first digit of the three-digit number on the card is odd.
The three-digit number on the card is divisible by 6.
A
50
B
33
C
25
D
12
Answers
The correct answer is 25 (option C), which indicates the number of cards that satisfy both conditions.
To determine the number of cards that satisfy both conditions, we need to find the count of three-digit numbers between 500 and 799 that are divisible by 6 and have an odd first digit.
For a number to be divisible by 6, it must be divisible by both 2 and 3. Since the first digit needs to be odd, it can be 5 or 7.
First, let's consider the case where the first digit is 5. The three-digit numbers starting with 5 and divisible by 6 are 510, 516, 522, ..., 798. To find the count of these numbers, we subtract the starting number (510) from the ending number (798) and divide by the common difference (6). This gives us (798 - 510) / 6 = 288 / 6 = 48.
Next, let's consider the case where the first digit is 7. The three-digit numbers starting with 7 and divisible by 6 are 714, 720, 726, ..., 798. Similarly, the count of these numbers is (798 - 714) / 6 = 84 / 6 = 14.
Adding the counts from both cases, we have 48 + 14 = 62. However, we need to exclude the number 756 from the count because it has an even first digit. So, the final count is 62 - 1 = 61.
Learn more about divide here:
https://brainly.com/question/30390300
#SPJ11
check my work (1 remaining) consider a sample with data values of21 , 20,17 ,9 ,16 ,12 and . round your answers to decimal place. compute the mean. compute the median.
Answers
The mean and median of the given data values are 15.8333 (approx) and 16.5 (approx) respectively.
Given data values = 21 , 20, 17 , 9 , 16 , 12 and
We are to compute the mean and median of the given data values.
For calculating mean of the given data values we need to use the formula given below:
Mean = (Sum of all data values) / (Total number of data values)
Or, Mean = ∑ xi / n,
where xi = ith data value,
n = total number of data values
Now, Sum of all data values = 21 + 20 + 17 + 9 + 16 + 12
= 95
Therefore, Mean = 95 / 6
= 15.8333 (approx)
Hence, the mean of the given data values is 15.8333 (approx).
Next, we need to calculate the median of the given data values.
The median is defined as the middlemost value of a data set or the average of the middle two values for a data set with an even number of values.
To find the median:
We need to first arrange the data values in ascending or descending order.
So, arranging the given data values in ascending order, we get: 9, 12, 16, 17, 20, 21
Next, to find the median we need to see if the number of data values is odd or even.
Since the total number of data values is even, we need to find the mean of the middle two data values.
Hence, the median of the given data values is (16 + 17) / 2 = 16.5 (approx).
Conclusion:
Therefore, the mean and median of the given data values are 15.8333 (approx) and 16.5 (approx) respectively.
To know more about median visit
https://brainly.com/question/300591
#SPJ11
if the second term of a geometric series is 48 and its fifth term is 6 then find the sum of its first term 6 terms
Answers
Answer:
The answer is 189.
Step-by-step explanation:
This geometric sequence is actually just a division of 2 for every term downwards. Therefore, we can see the first term is \(48 \cdot 2\) which is 96. Hence, we can work our way down from there:
List:
First term: 96
Second term: 48
Third term: 24
Fourth term: 12
Fifth term: 6
Sixth term: 3
Now, all we have to do is to add all the first 6 terms together to get:
\(96 + 48 + 24 + 12 + 6 + 3\)
\(= 189\)
The answer is 189.
Hope this helped!
the load l that a horizontal beam can safely support varies jointly as the width and the square of the depth d. if a beam with width 3 inches and depth 4 inches safely supports up to 220 pounds, how many pounds can a beam of the same length that has width 3 inches and depth 3 inches be expected to support? round to the nearest pound. assume the two beams are made of the same material.
Answers
The horizontal beam with different width and depth but of the same material will support 124 pounds.
Horizontal beam with width and square of the depth
Width = 3 inches
depth = 4 inches
Volume of the horizontal beam = 4 × 4 × 3
= 48 cubic inches
Second horizontal beam:
Width = 3 inches
depth = 3 inches
Volume of the second horizontal beam = 3 × 3 × 3
= 27 cubic inches
48 cubic inches support 220 pounds
⇒ 1 cubic inch support = 220 / 48 pounds
⇒27 cubic inches support = ( 220 / 48 ) × 27 pounds
⇒27 cubic inches support = 123.75 pounds
⇒27 cubic inches support = 124 pounds
Therefore, the horizontal beam with same length and different width and depth is equal to 124 pounds.
Learn more about width here
brainly.com/question/30282058
#SPJ4
If you put $15 a month in a CD for your new niece that will be born in 9 months, how much will she have when she is born?
Answers
Answer: 15 x 9 = 135
complete the square to rewrite the following equation in standard form
Answers
By completing the square, the equation in standard form is (x - 2)² + (y + 4)² = 4².
What is the equation of a circle?In Mathematics and Geometry, the standard form of the equation of a circle is modeled by this mathematical equation;
(x - h)² + (y - k)² = r²
Where:
h and k represent the coordinates at the center of a circle.r represent the radius of a circle.From the information provided below, we have the following equation of a circle:
x² - 4x + y² + 8y = -4
x² - 4x + (-4/2)² + y² + 8y + (8/2)² = -4 + (-4/2)² + (8/2)²
x² - 4x + 4 + y² + 8y + 16 = -4 + 4 + 16
(x - 2)² + (y + 4)² = 16
(x - 2)² + (y + 4)² = 4²
Therefore, the center (h, k) is (2, -4) and the radius is equal to 4 units.
Read more on equation of a circle here: brainly.com/question/15626679
#SPJ4
Complete Question:
Complete the square to rewrite the following equation in standard form. x² - 4x + y² + 8y = -4.
The 3 Rodgers sisters decided to pay off an old debt of $135.75 to their neighbor. If they all contribute the same amount of money, how much will each sister owe?
Answers
Because $132.75 divided by three equals 45.25
Δ WILL GIVE BRAINLIEST Δ
Write down 2-3 quotes to show gratitude to teachers to give an extra boost of energy and joy to the teachers and staff during this hard times.
Answers
Answer:
1. the best teacher
teach from the heart ❤️
not from the book
2. a good education can change anyone.
a good teacher can change everything.
3.teaching is a work of a Heart
Complete the solution of the equation. Find the
value of y when x equals 15.
-3x - y = -51
Answers
Step-by-step explanation:
Given:
x=15
To solve:
Simplify the equation.
Substitute 15 into x:
-3(15) - y = -51
-45-y=-51
Switch the terms to find y:
-45+51=y
6=y
Solution:
y=6.
Pls help me on this problem as soon as possible(if u don’t know pls do not answer
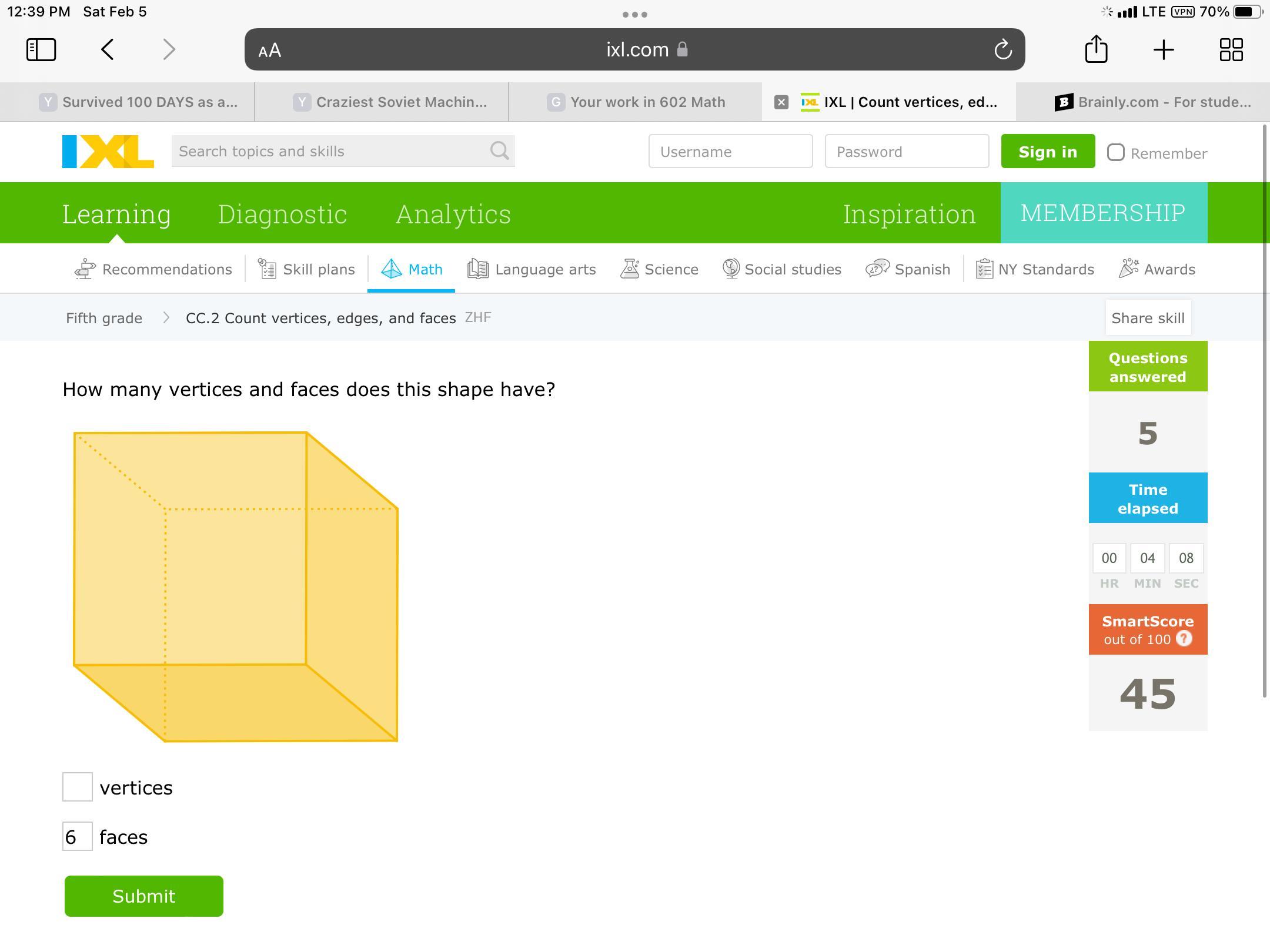
Answers
Write the equation of line with slope of -3, passing through (-1,7) . write in slope -intercept form.
Answers
Hello there, hope you are having a nice day.
We are given the slope of the line and a point on the line, so we can write the equation in point-slope form:
y-7=-3(x-(-1)
y-7=-3(x+1)
y-7=-3x-3
Now, we move -7 to the right side, using the opposite operation:
y=-3x-3+7
y=-3x+4
This is the equation of our line. Hope it helps.
Ask me if you have any queries.
~An emotional teen who helps others with joy
Good luck.
Please someone help please

Answers
Answer:
subtract
Step-by-step explanation:
Answer:
Its just to subtract and thats all.
fill in the table so it represents a linear function

Answers
Uhh, -4 , -6 , -8 im pretty sure.
PLEASE HELP
Rewrite 8 + 10 using the GCF and factoring.
2(8 + 10)
2(4 + 5)
4(2 + 3)
5(3 + 2)
Answers
The correct way of factorizing the sum is in the second option:
2*(4 + 5)
How to find the greatest common factor between the given numbers?
So we want to find the common factors between 8 and 10, so we can decompose these two numbers as a product of primes, we will get:
8 = 2*2*2
10 = 2*5
Notice that the only common factor is a "2"
Now we can rewrite the sum as:
8 + 10 = 2*4 + 2*5
Now we take the common factor using the distributive property:
8 + 10 = 2*4 + 2*5 = 2*(4 + 5)
The second option is the correct one.
If you want to learn more about common factors:
https://brainly.com/question/219464
#SPJ1
Rewriting 8 + 10 using the GCF and factoring will be 2( 4 + 5 )
The correct answer is B. That is, 2( 4 + 5 )
How can some numbers be Factorized ?To factorize numbers, the following must be done.
Look for common number among the numbersCheck for the factor of each numberCreate a bracketFactorize completely by placing the common number outside the bracketAccording to the question, we are told to rewrite 8 + 10 using the GCF and factoring.
What is the meaning of GCF ?
GCF means Greatest Common Factor
And the Greatest Common Factor of 8 + 10 is 2
Divide 8 by 2 that will give 4
Also, divide 10 by 2, that will give 5
Therefore, rewriting 8 + 10 using the GCF and factoring will be 2( 4 + 5 )
Learn more about Factorization here: https://brainly.com/question/25829061
#SPJ1
f(x) = x + 7
and
g(x) = x2
What is g( f(-9))
Answers
Answer:
4
Step-by-step explanation:
Answer:
g(f(-9))=4
Step-by-step explanation:
This is a composite function so we need to first find the value of the function on the inside in order find the value of the composite function
f(-9)=x+7=-9+7=-2
we can put -2 instead of f(-9) in the composite function
g(-2)=(-2)^2=4
1. |2x + z| + 2y
a = –2, b = –3, c = 2, x = 2.1, y = 3, and z = –4.2.
2. 4a – |3b + 2c|
Answers
Answer:
6 and -13
Step-by-step explanation:
Absolute ValueAbsolute Values are magnitudes (only positive values) of any values (be it positive or negative.)
Example: |4.5| = 4.5, |-6.7| = 6.7
Solution1. |2x + z| + 2y
= |2(2.1) + (-4.2)| + 2(3)
= |4.2 - 4.2| + 6
= 0 + 6
= 6
2. 4a - |3b + 2c|
= 4(-2) - |3(-3) + 2(2)|
= -8 - |-9 + 4|
= -8 - |-5|
= -8 - 5
= -13
Jane, kevin, and hans have a total of in their wallets. kevin has less than jane. hans has times what jane has. how much does each have?
Answers
Based on the given conditions, Jane has $31, Kevin has $25, and Hans has $50 in their wallets.
Let's solve the problem step by step.
First, let's assume that Jane has X dollars in her wallet. Since Kevin has $6 less than Jane, Kevin would have X - $6 dollars in his wallet.
Next, we're given that Hans has 2 times what Kevin has. So, Hans would have 2 * (X - $6) dollars in his wallet.
According to the information given, the total amount of money they have in their wallets is $106. We can write this as an equation:
X + (X - $6) + 2 * (X - $6) = $106
Simplifying the equation:
4X - $18 = $106
4X = $124
X = $31
Now we know that Jane has $31 in her wallet.
Substituting this value into the previous calculations, we find that Kevin has $31 - $6 = $25 and Hans has 2 * ($25) = $50.
To find the total amount they have, we sum up their individual amounts:
Jane: $31
Kevin: $25
Hans: $50
Adding these amounts together, we get $31 + $25 + $50 = $106, which matches the total amount stated in the problem.
To know more about Equation visit-
brainly.com/question/14686792
#SPJ11
The complete question is:
Jane, kevin and hans have a total of $106 in their wallets. kevin has $6 less than Jane. hans has 2 times what kevin has. how much do they have in their wallets?
Is the following number rational or irrational?
6.6
Choose 1 answer:
Answers
An airplane travels at a bearing of 100° (clockwise from North) at 180 km/hr. A wind redirects the plane, blowing at 30 km/hr at a bearing of 42°. Find the true speed of the plane and its new direction by modeling the speeds and directions as vectors.
Answers
The first step is converting both the velocity and the wind in vector form, as follows:
Velocity: \(\vec{v_1} = 180 \text{ km/hr} \angle 100^\circ\)Wind: \(\vec{v_2} = 30 \text{ km/hr} \angle 42^\circ\)Then the true speed of the plane is given by the addition of these two vectors, as follows:
\(\vec{v_1} + \vec{v_2} = \sqrt{|v_1|^2 + |v_2|^2 + 2 \cdot |v_1| \cdot |v_2| \cdot \cos(\theta)}\)
The magnitudes of each vector are given as follows:
\(|v_1| = 180\).\(|v_2| = 30\).The angle between these two vectors is given as follows:
\(\theta = 100^\circ - 42^\circ = 58^\circ\)
Thus the resulting speed is obtained as follows:
\(\vec{v_1} + \vec{v_2} = \sqrt{180^2 + 30^2 + 2 \cdot 180 \cdot 30 \cdot \cos(58^\circ)} = 197.54\)
The resulting angle of the plane is then obtained as follows:
\(\angle = \arctan\left(\frac{|v_1| \cdot \sin(\theta) + |v_2| \cdot \sin(\theta_2)}{|v_1| \cdot \cos(\theta) + |v_2| \cdot \cos(\theta_2)}\right)\)
Hence:
\(\angle = \arctan\left(\frac{180 \cdot \sin(58^\circ) + 30 \cdot \sin(42^\circ)}{180 \cdot \cos(58^\circ) + 30 \cdot \cos(42^\circ)}\right)\)
\(\angle = 59.87^\circ\)
More can be learned about vectors at https://brainly.com/question/25705666
#SPJ1
Answer:
197.5 km/h
Step-by-step explanation:
You want the resultant speed with an airplane at a speed of 180 km/h at 100° is acted upon by a wind at a speed of 30 km/h at 42°. Angles are bearings CW from north.
SolutionA vector calculator makes short work of this. The resultant speed is ...
197.5 km/h at 92.6°
Law of cosines
The law of cosines can be used to find the side opposite the known angle in the triangle with sides 30 km/h and 180 km/h. The known angle is ...
180° -(100° -42°) = 122°
So, the resultant speed is ...
c = √(a²+b²-2ab·cos(C))
= √(30² +180² -2(30)(180)·cos(122°)) ≈ √39023.13
c ≈ 197.543
The true speed of the plane is about 197.5 km/h.
__
Additional comment
You will notice that we used bearing angles directly in the calculator computation. As long as angles are consistently measured, it doesn't matter how they're measured.
When plotting the vectors on the Cartesian plane, we need to subtract the bearing angles from 90° to make them correspond to the vectors plotted on a map with north at the top.


What number should be multiplied by 5.8 so that the answer is 47.096?
Answers
Given
What number should be multiplied by 5.8 so that the answer is 47.096
Answer
Let x be multiplied to 5.8
\(\begin{gathered} 5.8x=47.096 \\ x=\frac{47.096}{5.8} \\ x=8.12 \end{gathered}\)Mr. Shaffer bought a block of fudge that weighed 8 3/4 pounds. He shared 2.45 pounds with his friends. How much does he have left?
Answers
Answer:
6.3 or 6 3/10 pounds
Step-by-step explanation:
First you convert 8 3/4 into a decimal.
8 3/4 = 8.75
You then subtract 8.75 and 2.45.
8.75 - 2.45 = 6.3
6.3 as a fraction is 6 3/10
Therefore, he has 6.3 or 6 3/10 pounds of fudge left.
Hope this helps:)
Find a function r(t) that describes the line segment from P(2,7,3) to Q(3,1,1). A. r(t)=⟨2−t,7+6t,3+2t⟩;0≤t≤1 B. r(t)=⟨2+t,7−6t,3−2t⟩;0≤t≤1 C. r(t)=⟨2+t,7−6t,3−2t⟩;1≤t≤2 D. r(t)=⟨2−t,7+6t,3+2t⟩;1≤t≤2
Answers
The correct function that describes the line segment from P(2,7,3) to Q(3,1,1) is r(t) = ⟨2 + t, 7 - 6t, 3 - 2t⟩; 0 ≤ t ≤ 1.
The function that describes the line segment from point P(2,7,3) to Q(3,1,1), we can use the parametric form of a line. The general form of a line equation is r(t) = ⟨x₀ + at, y₀ + bt, z₀ + ct⟩, where (x₀, y₀, z₀) is a point on the line and (a, b, c) are direction ratios.
1. First, we find the direction ratios by subtracting the coordinates of P from Q:
a = 3 - 2 = 1
b = 1 - 7 = -6
c = 1 - 3 = -2
2. Next, we substitute the point P(2,7,3) into the line equation and simplify:
r(t) = ⟨2 + t, 7 - 6t, 3 - 2t⟩
3. The parameter t represents the distance along the line segment. Since we want to describe the segment from P to Q, we need t to vary from 0 to 1, ensuring that we cover the entire segment.
4. Comparing the obtained equation with the given options, we find that the correct function is r(t) = ⟨2 + t, 7 - 6t, 3 - 2t⟩; 0 ≤ t ≤ 1.
Therefore, option A, r(t) = ⟨2 - t, 7 + 6t, 3 + 2t⟩; 0 ≤ t ≤ 1, is the correct answer.
Learn more about function : brainly.com/question/28278690
#SPJ11
HELP ME PLEASE!!!!!!
Beth enlarged the triangle below by a scale of 5. She found the area of the enlarged triangle. Her work is shown below.
What was Beth’s error?
She should have divided One-half (4) (3.5) by 5.
She should have divided One-half (4) (3.5) by 5 squared.
She should have multiplied (4) (3.5) by 5.
She should have multiplied One-half (4) (3.5) by 5 squared.


Answers
Answer:
The possible error made by Beth is directly multiplying scale of 5 to area of original triangle and getting area of enlarged triangle, which is wrong.
Step-by-step explanation:
Originally Triangle has height =3.5cm and width=4cm
Beth enlarged the same triangle by scale of 5 and calculate area of triangle
The area of triangle as given as A= $$\frac{1}{2} \texrm{ (base) (height)}$$
Area of original triangle is A =$$\frac{1}{2}(3.5 \times 4)$$
Since, The triangle is enlarged by scale of 5
New height =3.5x5 = cm and new width=4x5cm
Area of new triangle is
A' = $$\frac{1}{2} (\textrm{new width} ) ( \textrm{new height})$$
A' = $$\frac{1}{2}(3.5 \times 5)(4\times 5)$$
A' = $$\frac{1}{2}(3.5 \times 4)(5^{2})$$
A' = $$A (5^{2})$$
Now, Looking what error beth made is:
Beth found Area of new triangle is A' = $$\frac{1}{2}(3.5)(4)(5)$$
The possible error made by Beth is directly multiplying scale of 5 to area of original triangle and getting area of enlarged triangle, which is wrong.
Answer:
b
Step-by-step explanation:
Please help im really confused
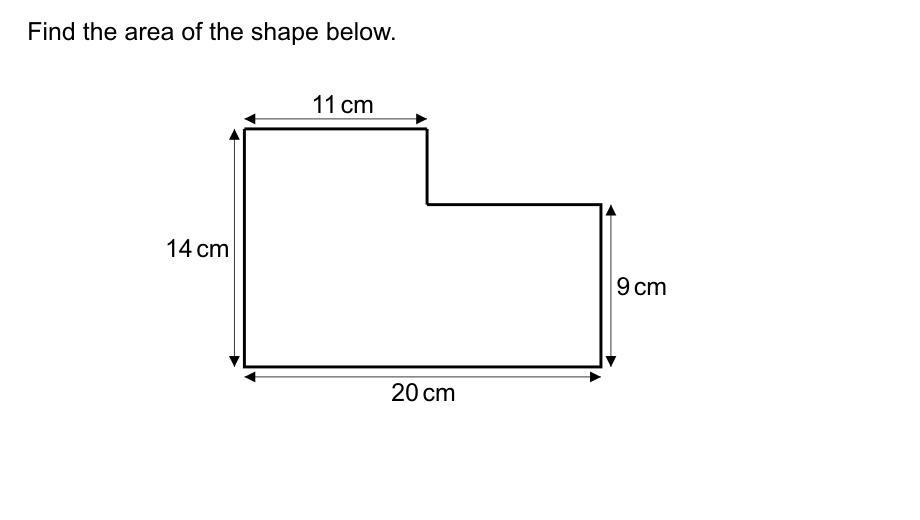
Answers
Answer:
A=235 cm 2
Step-by-step explanation:
A1=L x W
A1=9 x 20 180 + 55=235
A1=180cm 2
A2= L x W
A2=11 x 5
A2=55 cm2
Answer:
\(246 {cm}^{2} \)
hope this helps
brainliest appreciated
good luck! have a nice day!

in PQR if m∠p is 14 less than five times x, m∠q is five less than x and m∠r is nine less than twice x find x and the measure of each angle.
x=
m∠p=
m∠q=
m∠r=
Answers
The value of x =26°, m∠p =116°, m∠q=21°, m∠r=43°
What is an angle?
An angle is formed when two lines meets at the same vertex. It is measured by degree. Based on the measurements angles are of three types.
Consider POR as a triangle.
Given that m∠p=5x-14, m∠q=x-5, m∠r=2x-9.
In triangle the sum of the angle is 180°, then
m∠p + m∠q +m∠r =180°
⇒5x-14+x-5+2x-9 = 180°
⇒8x-28=180°
⇒x=26°
then, m∠p=5x-14 = 5(26)-14 = 116°
m∠q=x-5 = 26-5=21°
m∠r=2x-9 = 2(26)-9=43°
Hence, the value of x =26°, m∠p =116°, m∠q=21°, m∠r=43°
Learn more about angles here:
https://brainly.com/question/14690981
#SPJ1
GEOMETRY: PLEASE HELP!!!
A rectangle is removed from a right triangle to create the
shaded region shown below. Find the area of the shaded
region. Be sure to include the correct unit in your answer.
9cm
5cm
2cm
9cm

Answers
Answer:
30.5 or 61/2 cm²
Step-by-step explanation:
So the area of the figure is shown by this equation.
Area = Area of triangle - Area of rectangle cut out
= (0.5)(9)(9) - (2)(5)
= 40.5 - 10
= 30.5 or 61/2 cm²
(30.5 centimeters squared)

a right circular cone is inscribed in a right circular cylinder. the volume of the cylinder is $72\pi$ cubic centimeters. what is the number of cubic centimeters in the space inside the cylinder but outside the cone? express your answer in terms of $\pi$.
Answers
The number of cubic centimeters in the space which is inside the cylinder but outside the cone for given volume is equal to 72 cubic centimeters.
As right circular cone inscribed in a right circular cylinder.
Let A be the apex of the cone and B be the center of the base of the cone.
Let r be the radius of the base of the cone,
and let h be the height of the cone.
Let R be the radius of the base of the cylinder,
and let H be the height of the cylinder.
Volume of the cylinder = 72π cubic centimeters.
⇒ πR^2H = 72π
⇒ R^2H = 72
Base of the cone is a circle with radius r.
⇒ area of the base of the cone is πr^2.
Height of the cone is h.
Volume of the cone = 1/3 × πr^2h
Volume of the space inside the cylinder but outside the cone.
= volume of the cylinder - volume of the cone.
= πR^2H - 1/3 × πr^2h
Substituting R^2H = 72, we get,
⇒ Required Volume = 72π - 1/3 × πr^2h
Find r and h in terms of R and H.
Using the concept of similar triangles .
For similar triangle sides are in proportion.
⇒r/R = h/H
Solving for r, we get,
r = R × ( h/H )
Substituting this into the equation for the volume,
Volume = 72π - 1/3 × π(R × ( h/H ))^2h
Simplifying, we get,
⇒ Volume = 72π - 1/3 × πh^3R^2/H^2
Value of h that maximizes the volume.
Take the derivative of the volume with respect to h and set it equal to zero,
dV/dh = -2/3 × πh^2R^2/H^2
⇒ -2/3 × πh^2R^2/H^2= 0
Solving for h, we get,
⇒h = 0
Substituting this value of h back into the equation for the volume, we get,
⇒ Required Volume = 72π - 0
⇒ Required Volume = 72π cubic centimeters.
Therefore, the number of cubic centimeters in the space inside the cylinder but outside the cone is 72π cubic centimeters.
learn more about cylinder here
brainly.com/question/28384320
#SPJ4
if t is any real number it is possible that tan t = 5/4
Answers
It is possible for there to be a real number t such that tan(t) is equal to 5/4.
The tangent function (tan) is a periodic function that repeats its values every π radians or 180 degrees. It has both positive and negative values across its periodicity. Therefore, for any given value of tan(t), there are multiple solutions.
To find a specific angle where tan(t) is equal to 5/4, we can use inverse trigonometric functions. The inverse tangent function (arctan or \(tan^{-1}\)) can be used to find the angle associated with a given tangent value.
In this case, we can find an angle t such that tan(t) = 5/4 by taking the inverse tangent of 5/4. Using a calculator or mathematical software, we find that arctan(5/4) is approximately 51.34 degrees or approximately 0.896 radians.
Therefore, there exists a real number t such that tan(t) is equal to 5/4, specifically at approximately t = 51.34 degrees or t = 0.896 radians.
Learn more about periodic function here:
https://brainly.com/question/28223229
#SPJ11