a biologist collected 326 fern and moss samples. there were 66 fewer ferns than moss samples. how many fern samples did the biologist collect?
Answers
There are 130 fern samples did the biologist collect.
What is fern and moss samples?
In contrast to ferns, which are vascular plants, mosses are nonvascular primitive plants that produce spores. Furthermore, unlike ferns, which have a plant body that is divided into real stems, leaves, and roots, mosses have none of these features. Ferns also have circinate vernation, which is not true of mosses.
Given:
A biologist collected 326 fern and moss samples. there were 66 fewer ferns than moss samples.
Let, f denotes the number of ferns collected and
m denotes the number of mosses collected
From the given information,
m + f = 326 ..(1)
m - 66 = f ..(2)
Plug equation (2) in equation (1),
m + m - 66 = 326
2m = 326 + 66
2m = 392
m = 196
Plug m = 196 in equation (2),
f = 196 - 66
f = 130
Hence, there are 130 fern samples did the biologist collect.
To know more about fern and mosses, click on the link
https://brainly.com/question/14884573
#SPJ4
Related Questions
A business has gross sales of $300,000, sales returns of $5,000, cost of goods sold of $40,000, Operating expenses of $80,000, taxes of 30%. what is the pre tax profit.
Answers
Answer: 175,000
Step-by-step explanation:
Net Profit before Taxes = Gross Sales - Sales Returns - Cost of Goods Sold - Operating Expenses
= $300,000 - $5,000 - $40,000 - $80,000 = $175,000
Pre-Tax Profit = Net Profit before Taxes = $175,000.
Which expression is equivalent to 5x+10y-15?
5(x-2y-3)
5(x+5y-10)
5(x+2y-3)
5(x+2y-15)

Answers
Answer:Third optionoption
Step-by-step explanation:

Plzzz help me with this question and I also want working. Whoever will answer will be BRAINLIEST.

Answers
Answer:
\(for \: quadrilaeral \: \: sum \: of \: angles \: is \: equal \: 180 \times 2 = 360 \\ 80 + 70 + x + 2x = 360 \\ 3x = 360 - 70 - 80 = 210 \\ x = 210 \div 3 = 70 \\ q = 70 \\ r = 140\)
A student is asked to find the length of the hypotenuse of a right triangle. The length of one leg is 38 centimeters, and the length of the other leg is 21 centimeters. The student incorrectly says that the length of the hypotenuse is 7.7 centimeters
a. Find the length of the hypotenuse of the right triangle to the nearest tenth of a centimeter.
Answers
Hypotenuse = 43.4 cm
Find the equation for the tangent plane and the normal line at the point P_0(2, 1, 2) on the surface 2x^2 + 4y^2 +3z^2 = 24. Choose the correct equation for the tangent plane. A. 5x + 4y + 5z =24 B. 2x + 2y + 3z = 12 C. 2x+5y + 3z = 15 D. 5x+4y + 3z = 20 Find the equations for the normal line. x = y = z = (Type expressions using t as the variable.)
Answers
In multivariable calculus, the tangent plane is a plane that "touches" a surface at a given point and has the same slope or gradient as the surface at that point.
To find the equation for the tangent plane at the point P0(2, 1, 2) on the surface 2x^2 + 4y^2 +3z^2 = 24, we need to find the gradient vector of the surface at P0, which gives us the normal vector of the plane. Then, we can use the point-normal form of the equation for a plane to find the equation of the tangent plane.
The gradient vector of the surface is given by:
grad(2x^2 + 4y^2 +3z^2) = (4x, 8y, 6z)
At P0(2, 1, 2), the gradient vector is (8, 8, 12), which is the normal vector of the tangent plane.
Using the point-normal form of the equation for a plane, we have:
8(x - 2) + 8(y - 1) + 12(z - 2) = 0
Simplifying, we get:
4x + 4y + 3z = 20
Therefore, the correct equation for the tangent plane is D. 5x + 4y + 3z = 20.
To find the equations for the normal line, we need to use the direction vector of the line, which is the same as the normal vector of the tangent plane. Thus, the direction vector of the line is (8, 8, 12).
The equations for the normal line can be expressed as:
x = 2 + 8t
y = 1 + 8t
z = 2 + 12t
where t is a parameter that can take any real value.
To learn more about equation visit:
brainly.com/question/10413253
#SPJ11
Find the surface area of each pyramid show answer and round all decimals to the nearest tenth

Answers
The surface area of the pyramid is approximately 138.528 square feet.
What is the surface area of the pyramid?
The surface area of a solid is the sum of the areas of all faces of the solid. In this case, we find that the surface area is the sum of the areas of four triangles and the area of the square base. Then, we proceed to determine the surface area of the solid:
A = 4 · (1 / 2) · √[(3 ft)² + (8 ft)²] · (6 ft) + (6 ft)²
A ≈ 138.528 ft²
The surface area of the pyramid is approximately 138.528 square feet.
To learn more on surface areas: https://brainly.com/question/2835293
#SPJ1
How to prove it equal 8?

Answers
Answer:
The answer equals -8
Step-by-step explanation:
Order of Operations: BPEMDAS
FOIL - First, Outside, Inside, Last
Step 1: Write out expression
\((\sqrt{4-3i} -\sqrt{4+3i})^6\)
Step 2: Expand
\((\sqrt{4-3i} -\sqrt{4+3i})(\sqrt{4-3i} -\sqrt{4+3i})(\sqrt{4-3i} -\sqrt{4+3i})(\sqrt{4-3i} -\sqrt{4+3i})(\sqrt{4-3i} -\sqrt{4+3i})(\sqrt{4-3i} -\sqrt{4+3i})\)
Step 3: FOIL first 2
\((\sqrt{4-3i} -\sqrt{4+3i})^2 = -2\)
Step 4: Replace square roots with -2
-2(-2)(-2) = (-2)³ = 8
Identify the variable expression that is not a polynomial.
O A. 3 - 2
O B. 13
O C. y + 23
O D. x3
Answers
Answer:
the correct answer is d. x^3
Find the value of a in the equation below.
5 = x - 18
Answers
Answer:
There's no A so I'm going to assume you meant X
X = 23
Step-by-step explanation:
X is equal to 23, because 23 - 18 = 5
or 5 + 18 = 23
Dennis Anderson purchased four gallons of milk for $11.67. Find the unit price per gallon rounded to the nearest cent.
Answers
Answer:
$2.92
Step-by-step explanation:
Divde $11.67 by the 4 gallons that Dennis bought.
11.67/4=2.9175
round to the nearst cent (or hundreths place)
since 7 is greater than 5, it rounds up
$2.92
Find the directional derivative of the function at the given point in the direction of the vector v.
f(x, y) = 7 e^(x) sin y, (0, π/3), v = <-5,12>
Duf(0, π/3) = ??
Answers
The directional derivative of the function at the given point in the direction of the vector v are as follows :
\(\[D_{\mathbf{u}} f(\mathbf{a}) = \nabla f(\mathbf{a}) \cdot \mathbf{u}\]\)
Where:
- \(\(D_{\mathbf{u}} f(\mathbf{a})\) represents the directional derivative of the function \(f\) at the point \(\mathbf{a}\) in the direction of the vector \(\mathbf{u}\).\)
- \(\(\nabla f(\mathbf{a})\) represents the gradient of \(f\) at the point \(\mathbf{a}\).\)
- \(\(\cdot\) represents the dot product between the gradient and the vector \(\mathbf{u}\).\)
Now, let's substitute the values into the formula:
Given function: \(\(f(x, y) = 7e^x \sin y\)\)
Point: \(\((0, \frac{\pi}{3})\)\)
Vector: \(\(\mathbf{v} = \begin{bmatrix} -5 \\ 12 \end{bmatrix}\)\)
Gradient of \(\(f\)\) at the point \(\((0, \frac{\pi}{3})\):\)
\(\(\nabla f(0, \frac{\pi}{3}) = \begin{bmatrix} \frac{\partial f}{\partial x} (0, \frac{\pi}{3}) \\ \frac{\partial f}{\partial y} (0, \frac{\pi}{3}) \end{bmatrix}\)\)
To find the partial derivatives, we differentiate \(\(f\)\) with respect to \(\(x\)\) and \(\(y\)\) separately:
\(\(\frac{\partial f}{\partial x} = 7e^x \sin y\)\)
\(\(\frac{\partial f}{\partial y} = 7e^x \cos y\)\)
Substituting the values \(\((0, \frac{\pi}{3})\)\) into the partial derivatives:
\(\(\frac{\partial f}{\partial x} (0, \frac{\pi}{3}) = 7e^0 \sin \frac{\pi}{3} = \frac{7\sqrt{3}}{2}\)\)
\(\(\frac{\partial f}{\partial y} (0, \frac{\pi}{3}) = 7e^0 \cos \frac{\pi}{3} = \frac{7}{2}\)\)
Now, calculating the dot product between the gradient and the vector \(\(\mathbf{v}\)):
\(\(\nabla f(0, \frac{\pi}{3}) \cdot \mathbf{v} = \begin{bmatrix} \frac{7\sqrt{3}}{2} \\ \frac{7}{2} \end{bmatrix} \cdot \begin{bmatrix} -5 \\ 12 \end{bmatrix}\)\)
Using the dot product formula:
\(\(\nabla f(0, \frac{\pi}{3}) \cdot \mathbf{v} = \left(\frac{7\sqrt{3}}{2} \cdot -5\right) + \left(\frac{7}{2} \cdot 12\right)\)\)
Simplifying:
\(\(\nabla f(0, \frac{\pi}{3}) \cdot \mathbf{v} = -\frac{35\sqrt{3}}{2} + \frac{84}{2} = -\frac{35\sqrt{3}}{2} + 42\)\)
So, the directional derivative \(\(D_{\mathbf{u}} f(0 \frac{\pi}{3})\) in the direction of the vector \(\mathbf{v} = \begin{bmatrix} -5 \\ 12 \end{bmatrix}\) is \(-\frac{35\sqrt{3}}{2} + 42\).\)
To know more about derivative visit-
brainly.com/question/31422048
#SPJ11
-6 > v + 3/5 solve for the inequality for v and simplify your answer as much as possible
Answers
Answer: -33/5
Step-by-step explanation:
when using a graduated pipet, at which point do you measure the volume?
Answers
The volume is measured at the bottom of the meniscus when the liquid level is between the two etched marks on the pipet.
1. Place the graduated pipet on a flat surface and make sure it is level
2. Draw the liquid up until the meniscus is level with the etched line that corresponds to the desired volume
3. Make sure the liquid is not touching the etched line above it
4. Observe the bottom of the meniscus and take the reading at the point where the liquid level is between the two etched lines
The volume is measured at the bottom of the meniscus when the liquid level is between the two etched marks on the pipet.
Learn more about volume here
https://brainly.com/question/16134180
#SPJ4
Select the correct answer.
Describe the end behavior of the given function.
$(-) = 0) – 2
O A. As x decreases, (x) approaches 2.
OB.
As x decreases, Ax) approaches negative infinity.
OC. As xincreases, fx) approaches infinity.
OD. As x increases, Ax) approaches -2.

Answers
Answer:
answer is a
Step-by-step explanation:
Describe the end behavior of the given function.
$(-) = 0) – 2
O A. As x decreases, (x) approaches 2.
OB.
As x decreases, Ax) approaches negative infinity.
OC. As xincreases, fx) approaches infinity.
OD. As x increases, Ax) approaches -2
Answer:
C.
Step-by-step explanation:
(Use desmos graphing calculator to graph it...)
Find x.
A composite figure consisting of two right angled triangles lying next to each other. Two sides of the triangle on the left are labeled as 13 millimeters and 5 millimeters. Two sides of the triangle on the right are labeled as x and 35 millimeters.
Answers
The value of x is 28 millimeters in the composite figure of two right-angled triangles lying next to each other
What is a composite figure?A composite figure is a figure that is produced from the combination of two geometric shapes together.
The diagrammatic expression of a composite figure consists of two right-angled triangles lying next to each other can be seen in the image attached below.
For the left-side right-angled triangle, we have:
13² = h² + 5²
h² = 13² - 5²
h = √(169-25)
h = 12
Recall from the diagram that:
h² = pq
If p = 5 and q = x∴
12² = 5x
x = 144/5
x ≅ 28 millimeters
Learn more about composite figures here:
https://brainly.com/question/15981553
#SPJ1

A 50 foot ladder is set against the side of a house so that it reaches up 48 feet. If Mila grabs the ladder at its base and pulls it 6 feet farther from the house, how far up the side of the house will the ladder reach now
Answers
The ladder will reach up to a height of approximately 27.39 feet (rounded to two decimal places).
We can use the Pythagorean theorem to solve this problem. Let's call the distance from the base of the ladder to the house "x". Then, according to the Pythagorean theorem:
\(x^2 + 48^2 = 50^2\)
Simplifying this equation, we get:
\(x^2 + 2304 = 2500\)
Subtracting 2304 from both sides, we get:
\(x^2 = 196\)
Taking the square root of both sides, we get:
x = 14
So the ladder is currently 14 feet away from the house. If Mila pulls the ladder 6 feet farther away from the house, it will be 20 feet away from the house. We can use the same equation to find out how high up the ladder will reach:
\(x^2 + y^2 = 50^2\)
Substituting x = 20 and simplifying, we get:
\(y^2 = 1500\)
Taking the square root of both sides, we get:
y = 5√30
for such more question on height
https://brainly.com/question/27987869
#SPJ11
Please help me!
Use the quadratic formula, (image) to solve the equation. 2x2 − 8x + 7 = 0. Round to the nearest hundredths place.
x = −2.71 and x = −1.29
x = 1.29 and x = 2.71
x = −5.25 and x = 9.25
x = 5.17 and x = 10.83

Answers
The value of x in the quadratic equation using quadratic formula to the nearest hundredths place is x = 1.29 and x = 2.71.
The correct answer choice is option B.
How to solve quadratic equation?2x² - 8x + 7 = 0
\(x = \frac{ -b \pm \sqrt{b^2 - 4ac}}{ 2a }\)
\(x = \frac{ -(-8) \pm \sqrt{(-8)^2 - 4(2)(7)}}{ 2(2) }\)
\(x = \frac{ 8 \pm \sqrt{64 - 56}}{ 4 }\)
\(x = \frac{ 8 \pm \sqrt{8}}{ 4 }\)
\(x = \frac{ 8 \pm 2\sqrt{2}\, }{ 4 }\)
\(x = \frac{ 8 }{ 4 } \pm \frac{2\sqrt{2}\, }{ 4 }\)
\(x = 2 \pm \frac{ \sqrt{2}\, }{ 2 }\)
\(x = 2.70711\)
or
\(x = 1.29289\)
Hence,
Approximately, x = 1.29 or x = 2.71
Read more on quadratic formula:
https://brainly.com/question/1214333
#SPJ1
A. 1/3=0.33
B. 1/6=0.17
C. 1/10=0.10
D. 1/4=0.25

Answers
lmk if this helped
Carla has a rectangular garden in her backyard. The width of the garden is 9 meters. The area of the garden is 360 square meters. What is the length of the garden? Show your work.
Answers
Answer:
l = 40 m
Step-by-step explanation:
The formula for area of a rectangle is
A = lw, where
A is the area in square units,l is the length,and w is the widthStep 1: Since we're given the area and width, we plug in these two values for A and w and to solve for l (length):
360 = 9l
Step 2: Divide both sides by 9 to solve for l
(360 = 9l) / 9
40 m = l
Optional Step 3: We can check our answers by checking that the product of 40 and 9 is 360
40 * 9 = 360
360 = 360
Establish a BN structure model with more than 10 nodes, and explain what is the meaning of the structure.
Answers
The BN structure model with more than 10 nodes can be established. The structure refers to the way the variables are related.
A Bayesian Network (BN) is a probabilistic graphical model that illustrates a set of variables and their probabilistic dependencies. A BN structure is made up of nodes and edges. Nodes represent variables, and edges represent the connections between the variables. The BN structure model can be established by using various algorithms, including structure learning and parameter learning.The BN structure with more than 10 nodes is a complex model with numerous variables and their dependencies. The structure's meaning is how the variables are interrelated, allowing us to estimate the probabilities of certain events or scenarios. The nodes in the structure represent various factors that affect the outcome of an event, and the edges between them demonstrate how these factors are related.The BN structure model is used in many fields, including medical diagnosis, fault diagnosis, and decision making.
The Bayesian Network structure model with more than 10 nodes is a powerful tool for analyzing complex systems. It helps to understand the interrelationships between variables and estimate the probabilities of different events or scenarios. This model is useful in various fields and provides insights into many complex phenomena.
To know more about Nodes visit:
brainly.com/question/32227668
#SPJ11
find the slope of line through points (4,-4) and (9,-4)

Answers
Step-by-step explanation:
Slope is equal to the change in y over the change in x, or rise over run.
\(m = \frac{change \: in \: y}{change in \: x\: } \)
The change in x is equal to the difference in x-coordinates (also called run), and the change in y is equal to the difference in y-coordinates (also called rise).
\(m = \frac{y2 - y1}{x2 - x1} \)
Substitute in the values of x and y into the equation to find the slope.
\(m = \frac{ - 4 - ( - 4)}{9 - (4)} \)
Simplify.
\(m = 0\)
Therefor, The slope is 0.

Answer:
Slope: 0
Step-by-step explanation:
The formula to finding slope is \(\frac{y1-y2}{x1-x2}\)
We have the points (4,-4) and (9,-4)
So plug in:
\(\frac{-4-(-4)}{4-9}\)
Simplify:
\(\frac{0}{-5}\)
Slope: 0
Help please…………………………..

Answers
Answer:
the first one
Step-by-step explanation:
It passes the vertical line test
Answer: The first one.
Step-by-step explanation:
So that AM:MB = 3:2 and N is the midpoint of
CM
If the area of △CNB is 35 in2, find the area of △CMB, △AMC, and △ABC
Answers
Area of △CMB ≈ 23.33 in² ,Area of △AMC ≈ 52.50 in²,Area of △ABC ≈ 75.83 in².
The problem step by step.
Given that AM:MB = 3:2, we can express the areas of triangles △CMB, △AMC, and △ABC in terms of their corresponding sides.
1. Area of △CNB = 35 in²
Since N is the midpoint of CM, we know that the ratio of the areas of △CNB and △CMB is the same as the ratio of their corresponding bases. Therefore, the area of △CMB can be determined as follows:
Area of △CMB = (2/3) * Area of △CNB = (2/3) * 35 = 70/3 in² ≈ 23.33 in²
2. Area of △AMC
Since AM:MB = 3:2, we can consider the area ratio as the square of the side ratio. Therefore, the area of △AMC can be determined as follows:
Area of △AMC = (3/2)² * Area of △CMB = (9/4) * (70/3) = 630/12 in² ≈ 52.50 in²
3. Area of △ABC
The area of △ABC can be obtained by summing the areas of △CMB and △AMC:
Area of △ABC = Area of △CMB + Area of △AMC = 70/3 + 630/12 = 280/12 + 630/12 = 910/12 in² ≈ 75.83 in²
To summarize:
Area of △CMB ≈ 23.33 in²
Area of △AMC ≈ 52.50 in²
Area of △ABC ≈ 75.83 in²
For more questions on Area .
https://brainly.com/question/2607596
#SPJ8
Find the ratio of 125gm:2kg
Answers
Step-by-step explanation:
Convert kilogram into gram first.
\(1 kg = 1000g\)
\(2kg = 1000 \times 2 \\ = 2000\)
a:b = a/b
125:2000= 125/2000
If u divide u get
1/16
a:b = a/b
1/16= 1:16
Ratio is now found.
Answer:
2 kg = 2000 gms
So, ratio of 2kg to 250 gms is 2000/250 = 8:1 or we can write
2kg:250::8:1
In words, we say 2 kg or 2000 gms to 250 gms ratio is as 8 is to 1
Step-by-step explanation:
was it helpful
A model of a skyscraper is made using a scale of 1 inch: 75 feet. What is the height of the actual building if the height of the model is 19 2/5 inches?

Answers
Then 60 ft = 60 x 1/8 = 7.5 in
Length of model = 7.5 in
Scale factor = 1/8
5. If 4 m = 1 cm
Then 192 m = 192/4 x 1 = 48 cm
Length of model = 48 cm
Scale factor = 1/4
6. If 1.5 ft = 2 in
Then 13.5 ft = 13.5 x2/1.5 = 18 in
Length of model = 18 in
Scale factor = 2/1.5 =1.333
Skyscraper
Scale = 1 in : 75 ft
Height of model= 19 2/5in=19.4in
Height of actual building
19.4 x 75 = 1455 ft
Determine whether the statement is true or false. If the statement is false, explain why. The midpoint of the segment joining (0,0) and (38,38) is 19.
Answers
The midpoint has coordinates (19,19) as per the midpoint formula.
The statement is false.
The statement is false. The midpoint of the segment joining two points is determined by taking the average of their x-coordinates and the average of their y-coordinates. In this case, the two given points are (0,0) and (38,38).
To find the x-coordinate of the midpoint, we take the average of the x-coordinates of the two points:
(x1 + x2) / 2
= (0 + 38) / 2
= 38 / 2
= 19
Therefore, the x-coordinate of the midpoint is 19, which matches the statement. However, to determine if the statement is true or false, we also need to check the y-coordinate.
To find the y-coordinate of the midpoint, we take the average of the y-coordinates of the two points:
(y1 + y2) / 2
= (0 + 38) / 2
= 38 / 2
= 19
The y-coordinate of the midpoint is also 19. Therefore, the coordinates of the midpoint are (19,19), not 19 as stated in the statement. Since the midpoint has coordinates (19,19), the statement is false.
To learn more about the midpoint;
https://brainly.com/question/28224145
#SPJ4
Determine the equivalent expression. Apply the distributive property and then combine like terms. Look at each step to see which are equivalent. Select all that apply 8+3(2x+5)

Answers
The given expression is
\(8+3(2x+5)\)\(Use\text{ the distribustive law , a}\times(b+c)=a\times b+a\times c.\)\(8+3(2x+5)=8+3(2x)+3(5)\)The first option is correct.
\(8+3(2x+5)=8+6x+15\)The fourth option is correct.
Adding 8 and 15, we get
\(8+3(2x+5)=23+6x\)The second option is correct.
Can someone help me solve this please?
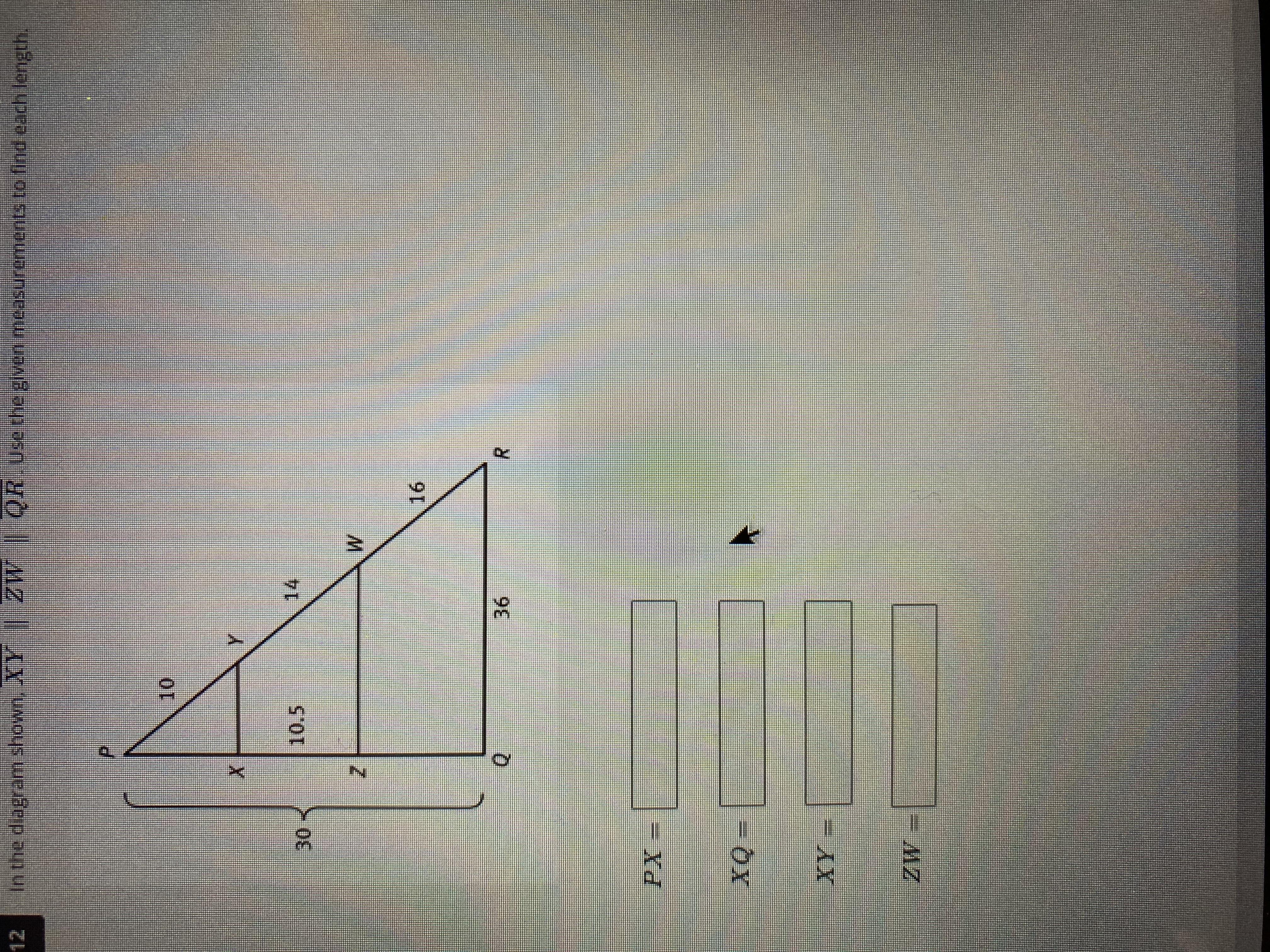
Answers
The segment lengths for this triangle are given as follows:
PX = 7.5.XQ = 22.5.XY = 9.ZW = 21.6. What are similar triangles?Similar triangles are triangles that share these two features given as follows:
Congruent angle measures.Proportional side lengths.There are three triangles in this problem, all of which are similar.
PQR.PZW.PXY.The length of segment PX can be obtained with triangles PQR and PXY, as follows:
PX/30 = 10/40
PX/30 = 1/4
4PX = 30
PX = 7.5.
The length of segment XQ is found applying the segment addition postulate, as follows:
PQ + XQ = 30
7.5 + XQ = 30
XQ = 22.5.
The length of segment XY can also be obtained with the similarity of triangles PXY and PQR, as follows:
XY/36 = 10/40
XY/36 = 1/4
4XY = 36
XY = 9.
The length of segment ZW is obtained with the similarity of triangles PZW and PQR, as follows:
ZW/36 = 24/40
ZW/36 = 0.6.
ZW = 36 x 0.6
ZW = 21.6.
More can be learned about similar triangles at brainly.com/question/14285697
#SPJ1
A.Find the values for j and k
B.Write an equation for f(x)

Answers
well, let's move like the crab, backwards, let's start with b), then we'll do a)
b)
\({\Large \begin{array}{llll} y=ab^x \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \begin{cases} x=2\\ y=75 \end{cases}\implies 75=ab^2 \\\\[-0.35em] ~\dotfill\\\\ \begin{cases} x=5\\ y=9375 \end{cases}\implies 9375=ab^5\implies 9375=ab^{2+3}\implies 9375=ab^2 b^3\)
\(\stackrel{\textit{substituting from the 1st equation}}{9375=\underset{ab^2}{(75)} b^3}\implies \cfrac{9375}{75}=b^3\implies 125=b^3 \\\\\\ \sqrt[3]{125}=b\implies \boxed{5=b}\hspace{5em}\stackrel{\textit{we know that}}{75=ab^2}\implies 75=a5^2\implies 75=25a \\\\\\ \cfrac{75}{25}=a\implies \boxed{3=a}\hspace{5em} {\Large \begin{array}{llll} y = 3(5^x) \end{array}}\)
a)
\(\begin{cases} x=0\\ y=j \end{cases}\implies j=3(5^0)\implies j=3(1)\implies j=3 \\\\\\ \begin{cases} x=4\\ y=k \end{cases}\implies k=3(5^4)\implies k=3(625)\implies k=1875\)
Picture is there only answer number 7.

Answers
Surface area = ft^2
Volume = cm^3
Perimeter = in.
Explanation
Area is L x W so it is squared or
power of ^2
Volume is L x W x H so it is cubic or
power of ^3
Perimeter is 2L + 2W so it is inches,
no exponent