80% of a number is x. What is 100% of the number? Assume x > 0.
Answers
Related Questions
A rectangular room is 7 times as long as it's wide and it's perimeter is 64metres. Find the dimension of the room.
Answers
Answer:
Length = 28 meters Width = 4 metersStep-by-step explanation:
Assume the width of the rectangle is x. That means that the length of the rectangle is 7x which is 7 times as long as it is wide.
Perimeter of a rectangle:
= Length + length + Width + Width
Therefore:
7x + 7x + x + x = 64
16x = 64
x = 64/16
x = 4 meters
Length is 7 times as long:
= 4 * 7
= 28 meters
What is the factor of x³ 3x² 9x 5?
Answers
(x+1) & (x-5) are the factors of given equation.
The given Equation is,
x3- \(3x^{3}\) - 9
Substitute - Substitute means to put something in the place of another and in mathematics substitution means putting numbers in the place of letters. It is used to calculate the value of an expression.Here, If we substitute x =5, in the given equation, then we find
(5)3 - 3(5)3 - 9*5 -5 = 0
x-5 is factor of given equation to find another factor dividing given equation by x-5
we will get =(x2+2x+1) after dividing the equation by x - 5
Hence x3- \(3x^{3}\) - 9 =(x2+2x+1) (x-5)
=(x+2)2 (x-5)
To learn more about Equation click the link
brainly.com/question/29657983
#SPJ4
The Furry Friends Hotel, a kennel in Sparrowtown, needs to bring in at least $1,100 per day to cover its operating costs. The kennel charges $26 per day to house a large dog and $23
per day to house a small dog.
write an inequality to represent the situation
Answers
Answer:
23x >= 1100
Step-by-step explanation:
Use the divergence theorem to find the outward flux of F across the boundary of the region D. F=(y−4x)i+(5z−y)j+(4y−2x)k D: The cube bounded by the planes x=±2,y=±2, and z=±2
Answers
The outward flux of F across the boundary of the cube D is -128.
To find the outward flux of F across the boundary of the region D using the divergence theorem, we need to evaluate the surface integral of the divergence of F over the surface of the cube.
The divergence theorem states that for a vector field F and a region D with a closed surface S, the outward flux of F across S is equal to the triple integral of the divergence of F over the volume enclosed by S.
First, let's calculate the divergence of F:
div(F) = ∇ · F = ∂(y-4x)/∂x + ∂(5z-y)/∂y + ∂(4y-2x)/∂z
= -4 + 0 + 0
= -4
The outward flux of F across the boundary of the cube D is then given by the surface integral:
∬S F · dS = ∭V div(F) dV
Since the region D is a cube bounded by the planes x=±2, y=±2, and z=±2, we can express the triple integral as follows:
\(∭V div(F) dV = ∫-2^2 ∫-2^2 ∫-2^2 (-4) dx dy dz\)
Evaluating this triple integral, we get:
\(∫-2^2 ∫-2^2 ∫-2^2 (-4) dx dy dz = (-4) ∫-2^2 ∫-2^2 [x] dy dz\)
\(= (-4) ∫-2^2 [xy] dy dz\)
\(= (-4) ∫-2^2 [2xy] dz\)
\(= (-4) [2xyz] |-2^2\)
= (-4) [2(2)(2) - 2(-2)(2)]
= (-4) [16 - (-16)]
= (-4) [32]
= -128
Therefore, the outward flux of F across the boundary of the cube D is -128.
Learn more about divergence theorem here:
https://brainly.com/question/31272239
#SPJ11
3n + 9 = 11n -23 Please
Answers
Answer: N=4
Step-by-step explanation:
Answer: n = 4
Step-by-step explanation:
subtract 9 from both sides simplify subtract 11n from both sides then combine like terms, simplify, divide both sides by the same factor, then simplify then boom :)
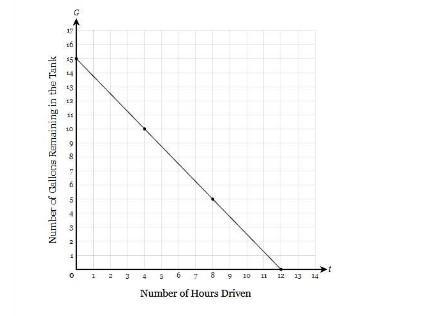
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
What’s the answer plsss asp

Answers
The right angle, or 90°, is always one angle. The hypotenuse is the side with the 90° angle opposite.
If the side of DF = 7.7 cm then DE = 3.7 cm.
What is meant by right angle triangle?The right angle, or 90°, is always one angle. The hypotenuse is the side with the 90° angle opposite. The longest side is always the hypotenuse. The other two inner angles add up to 90 degrees.
A right triangle is a triangle in which one of the angles is at a right angle or two of the sides are perpendicular, or more formally, an orthogonal triangle, formerly known as a rectangled triangle. The foundation of trigonometry is the relationship between the sides and various angles of the right triangle.
Given: DF = 7.7 cm and ∠ E = 29°
Let the equation be
sin θ = P/h = DF / DE
substitute the values in the above equation, we get
⇒ sin 29° = 7.7 / DE
⇒ DE = 7.7 / 0.48 = 3.696 = 3.7 cm
Therefore, the correct answer is option a) 3.7 cm.
To learn more about right angle triangle refer to:
https://brainly.com/question/64787
#SPJ13
\(\frac{tan(\frac{-2π}{3}} {sin\frac{7π}{4}} -sec (-π)\\\)What is the exact value of the trigonometric expression? State your answer in simplified radical form
Answers
The exact value of the trigonometric expression \(\frac{tan-(2\pi/3) }{sin(7\pi /4)} - sec(-\pi )\) in the simplified radical form is √6 + 1.
\(\frac{tan-(2\pi/3) }{sin(7\pi /4)} - sec(-\pi )\)
We have the angle,
-2π/3 = -120° = (360 - 120)° = 240° = 60°
Put the value of -2π/3 in tan -2π/3, we get
tan -2π/3 = tan (60) = √3
7π/4 × 180/π = 7 × (180/4) = 7 × 45 = 315° = 45°
Put the value of 7π/4 in sin 7π/4, and we get
sin 7π/4 = sin (45°) = √2/2
sec (-π) = sec (π) = -1
Now, substitute all the values in the given equation,
= {√3/(√2/2)} - (-1)
= (2√3/√2) + 1
= (2√3 × √2/√2 × √2) +1
= (2√6/2) + 1
= √6 + 1
--The given question is incorrect, the correct question is
''What is the exact value of the trigonometric expression? \(\frac{tan-(2\pi/3) }{sin(7\pi /4)} - sec(-\pi )\) State your answer in simplified radical form."--
To know more about trigonometric expression, here
https://brainly.com/question/11659262
#SPJ4
Does anyone know what is going on with this website? So many hackers, trolls, and people giving non answers to the questions asked! It didn't used to be this way. :(
Answers
Answer:
Lots of people are just answering to get free points now, they're not actually giving answers.
(and sorry if you miss the way it used to be).
On a coordinate plane, a line is drawn from point a to point b. point a is at (negative 8, negative 13) and point b is at (4, 11). what are the x- and y- coordinates of point p on the directed line segment from a to b such that p is one-third the length of the line segment from a to b? x = (startfraction m over m n endfraction) (x 2 minus x 1) x 1 y = (startfraction m over m n endfraction) (y 2 minus y 1) y 1 (1, 5) (0, 3) (–4, –5) (–5, –7)
Answers
The coordinate for point P which is one-third the length of the line segment from a to b is (-4, -5)
What is an equation?An equation is an expression that shows the relationship between two or more variables and numbers.
Point a is at (-8, -13) and point b is at (4, 11). Hence the coordinates for point p(x, y) which is one-third the length of the line segment from a to b is:
\(x=\frac{1}{3}(4-(-8))+(-8)=-4\\ \\y=\frac{1}{3}(11-(-13))+(-13)=-5\)
The coordinate for point P which is one-third the length of the line segment from a to b is (-4, -5)
Find out more on equation at: https://brainly.com/question/2972832
#SPJ4
Answer:
-4, -5
Step-by-step explanation:
As an estimation we are told £3 is $5.
What is the conversion rate from $ to £?
Give your answer rounded to 2 DP.
Answers
Answer:
the conversion rate from £ to $ is 1£ = 1.67$
Step-by-step explanation:
the conversion rate from £ to $ is 1£ = 1.67$
Parallelograms lifts are used to elevate large vehicle for maintenance. Two consecutive angles
of a parallelogram have measures 3(2 + 10)
° and 4( + 10)
°
, respectively. Find the measures
of the angles.
A. 96° and 84° B. 98° and 82° C. 100° and 80° D. 105° and 75
Answers
The fourth angle is also x degrees, or approximately 40.57 degrees. The closest answer choice to these measures is C. 100° and 80°.
To solve this problem, we need to remember that opposite angles in a parallelogram are congruent. Let's call the measure of the third angle x. Then, the fourth angle is also x degrees.
Using the given information, we can set up an equation:
3(2+10) + x + 4(x+10) = 360
Simplifying and solving for x, we get:
36 + 3x + 40 + 4x = 360
7x = 284
x ≈ 40.57
Therefore, the measures of the angles are:
3(2+10) = 36 degrees
4(x+10) = 163.43 degrees
x = 40.57 degrees
And the fourth angle is also x degrees, or approximately 40.57 degrees.
The closest answer choice to these measures is C. 100° and 80°.
To know more about parallelogram visit :
https://brainly.com/question/28854514
#SPJ11
An electronics store sells an average of 117 home theater systems per month at a price of $213 each. When the store drops its price to $192, it sells 28 home theater systems more each month. At what price should the store sell the home theater systems to maximize its revenue?
Answers
The optimal price at which the store should sell the home theater systems to maximize its revenue is $192.
To determine the price at which the store should sell the home theater systems to maximize its revenue, we need to analyze the relationship between price, quantity sold, and revenue.
Let's denote the original price as P1 ($213) and the new price as P2 ($192). The original quantity sold is Q1 (117), and the increased quantity sold is Q2 (117 + 28 = 145).
The revenue (R) can be calculated as the product of price and quantity sold:
R = Price × Quantity Sold
First, let's calculate the revenue at the original price (P1) and quantity sold (Q1):
R1 = P1 × Q1 = $213 × 117
R1 = $24,921
Next, let's calculate the revenue at the new price (P2) and quantity sold (Q2):
R2 = P2 × Q2 = $192 × 145
R2 = $27,840
Now, we compare the revenues R1 and R2 to determine which one is higher. If R2 is higher than R1, the store should sell the home theater systems at the new price (P2). If R1 is higher, the store should continue selling at the original price (P1).
Comparing R1 and R2, we see that R2 ($27,840) is higher than R1 ($24,921). Therefore, the store should sell the home theater systems at the new price of $192 to maximize its revenue.
In order to maximise its revenue, the business should sell the home theatre systems for $192.
for such more question on original price
https://brainly.com/question/7459025
#SPJ8
Suppose the following lotteries.
⚫ Lottery A gives $2 million with 10%, $1 million with 80%, and $0 with 10%.
⚫ Lottery B gives $2 million with 12%, $1 million with 3%, and $0 with 82%.
⚫ Lottery C gives $2 million with 40%, $1 million with 10%, and $0 with 40%.
⚫ Lottery D gives $2 million with 3%, $1 million with 24%, and $0 with 73%.
Show one example of preference relations which violate Independence of the expected utility theorem, and explain the reason.
Answers
The introduction of B should not have impacted the preference between A and C.
Preference relations that violate Independence of the expected utility theorem:
Independence of irrelevant alternatives (IIA) refers to a preference relation principle that states that the decision maker's preference between two choices should be the same, regardless of the presence or absence of a third, unrelated option.
Suppose the following preferences:
Lottery A: 0.1 chance to win $2,000,000, 0.8 chance to win $1,000,000, 0.1 chance to win nothing
Lottery B: 0.12 chance to win $2,000,000, 0.03 chance to win $1,000,000, 0.85 chance to win nothing, and
Lottery C: 0.4 chance to win $2,000,000, 0.1 chance to win $1,000,000, 0.4 chance to win nothing.
Lottery A over B: A is chosen over B with probability 1
Lottery C over A: C is chosen over A with probability 0.5
Lottery C over B: C is chosen over B with probability 0
Suppose you're trying to decide between A and B, and you choose A. This implies that you have a specific preference between the two options. Similarly, if you choose C over A, it implies that you have a specific preference between those two options as well.
However, if you now compare C to B, you'll see that C is selected over B with probability 0, indicating that there is no preference between the two alternatives. This is in violation of the Independence of irrelevant alternatives theorem because the introduction of B should not have impacted the preference between A and C. Thus, this violates the Independence of the expected utility theorem.
Learn more about probability at
https://brainly.com/question/29176120
#SPJ11
Problem of Tartaglia (1500-1577): among all positive numbers a, b whose sum is 8, find those for which the product of the two numbers and their difference is largest. (Enter your answers as a comma-separated list.)
a, b = _____
Let x = a - b and express abx in terms of x alone.
Answers
As per the information provided, a = 4√3/3 + 4, b = 4 - 4√3/3 the answer can be calculated with optimization method. it will be as follows:
Sum of a and b is 8, we get
a+b=8
b=8−a
Now, let x=a−b
Then we get,
\(x=a−(8−a) \\ x=2a−8 \\ x+8=2 \\ 1 \div 2x+4=a
\)
we use this to answer to solve for b
\(b=8−a \\ =8−(1 \div 2x+4) \\ =4−1 \div 2x
\)
Now we use the product of two numbers and its difference. This can be expressed as:
\(a⋅b⋅x=(1 \div 2x+4)(4−1 \div 2x) \\ x=2 {x}^{2} − \frac{1}{4} {x}^{3} +16x−2x^{2} \\ =−14x^{3} +16x
\)
Thus, this expression that we need to maximize. Take the derivative, set it equal to zero, and solve for x
\(−3 \div 4x ^{2} +16=0 \\ 16 =3 \div 4 x ^{2} \\ 643=x \\ 28√3 \div 3=x\)
Now for us to check that this is a maximum, we have to note that the second derivative is
\(−3 \div 2x
\\ At \\
x=8√3 \div 3
\)
the second derivative is −4√3. Since this number is negative, the point is a maximum.
Now we must find the values of a and b for this x. We have to use the relationship
\(a=1 \div 2x+4\)
\(a=1 \div 2 \times 8√3 \div 3+4 \\ =4√3 \div 3+4\)
now we use the relationship b=8−a
\(b=8−(4√3 \div 3+4) \\ =4−4√3 \div 3\)
The first step in determining a function's maximum or minimum value is differentiating it. Then, set this derivative to zero and conduct the computation.
x. This will reveal the location of a function's maximum or minimum, but it won't reveal which.
Take the second derivative to get more details. A local maximum occurs when both the first and second derivatives are negative. You have a local minimum when both the first derivative and the second derivative are zero.
To learn more about optimization: https://brainly.com/question/28970005
#SPJ4
MATH FRACTIONS!!
What is 3/4 divided by 5/6 how to solve it the step by step. I NEED IT
Answers
Answer:
9/10
Step-by-step explanation:
the rule says
\(\frac{a}{b} /\frac{c}{d} =\frac{ad}{bc}\)
so in our case
a=3
b=4
c=5
d=6
so the division is
\(\frac{3*6}{4*5} \\\\=\frac{18}{20}\)
we can simplify
\(\frac{18}{20} \\\\=\frac{2(9)}{2(10)} \\\\=\frac{9}{10}\)
that's our answer
I don't know if you need step by step of the rule, if you need let me know
The division of the fractions are solved and A = 9/10
Given data ,
Let the equation be represented as A
Now , the value of A is
Let the numerator of the fraction be p
where the value of p = ( 3/4 )
Let the denominator of the fraction be q
where q = ( 5/6 )
Now , the fraction is A = p/q
On simplifying the expression , we get
So , the left hand side of the equation is equated to the right hand side by the value of p/q
A = ( 3/4 ) / ( 5/6 )
A = ( 3/4 ) x ( 6/5 )
On further simplification , we get
A = ( 18 / 20 )
A = 9/10
Therefore , the value of A = 9/10
Hence , the fraction is A = 9/10
To learn more about fractions click :
https://brainly.com/question/29766013
#SPJ6
Someone pls help me

Answers
Lashonda drove 495 miles in 9 hours.
At the same rate, how many miles would she drive in 13 hours?
Answers
Answer:
715 miles
Step-by-step explanation:
We Know
Lashonda drove 495 miles in 9 hours.
495 / 9 = 55 miles per hour
At the same rate, how many miles would she drive in 13 hours?
We Take
55 x 13 = 715 miles
So, she drives 715 miles in 13 hours.
\(\begin{array}{ccll} miles&hours\\ \cline{1-2} 495 & 9\\ m& 13 \end{array} \implies \cfrac{495}{m}~~=~~\cfrac{9}{13} \\\\\\ (495)(13)=9m\implies \cfrac{(495)(13)}{9}=m\implies 715=m\)
Question 5 (5 points)
What is the volume of the right prism?
35 in.
37 in.
12 in.
40 in.

Answers
The volume of the right prism include the following: 8,640 in³.
How to calculate the volume of a rectangular prism?In Mathematics and Geometry, the volume of a rectangular prism can be calculated by using the following formula:
Volume of a rectangular prism = L × W × H
Where:
L represents the length of a rectangular prism.W represents the width of a rectangular prism.H represents the height or depth of a rectangular prism.Next, we would determine the area of the triangle at the base of the right prism as follows:
Base area = 1/2 × ( 36 × 12)
Base area = 1/2 × 432
Base area = 216 in².
Now, we can calculate the the volume of this right prism:
Volume = base area × height
Volume = 216 × 40
Volume = 8,640 in³.
Read more on right prism here: https://brainly.com/question/31245490
#SPJ1
The set R is a two-dimensional subspace of R3.Choose the correct answer below A. False, because R2 is not closed under vector addition. B. True, because R2 is a plane in R3 C. False, because the set R2 is not even a subset of R3 D. True, because every vector in R2 can be represented by a linear combination of vectors inR3
Answers
The statement "The set R is a two-dimensional subspace of R3" is False because R2 is not closed under vector addition. The correct answer is A. False, because R2 is not closed under vector addition.
To determine if the statement is true or false, we need to understand the properties of subspaces. A subspace must satisfy three conditions: it must contain the zero vector, be closed under vector addition, and be closed under scalar multiplication.
In this case, R is a two-dimensional subspace of R3. R2 refers to the set of all two-dimensional vectors, which can be represented as (x, y). However, R2 is not closed under vector addition in R3. When two vectors from R2 are added, their resulting sum may have a component in the third dimension, which means it is not in R2. Therefore, R2 does not meet the condition of being closed under vector addition.
To learn more about vector addition, refer:-
https://brainly.com/question/23867486
#SPJ11
WILL MARK BRAINIEST.
Draw a line representing the rise and a line representing the run of the line state the slope of the line in simplest form. NOTE- please draw a line clearly showing the rise and run and what the slope is thanks

Answers
Answer:
y=-3/2+6 (slope is -3/2)
Step-by-step explanation:
Find a point and use the rise/run method.
You go up 3 and left 2. This makes your slope
The b is 6 because that's where the line hits the y-axis
pleasee helpp
5(x − 2) + 2 = 5x − 8

Answers
Answer:
infinite solutions
Step-by-step explanation:
5(x − 2) + 2 = 5x − 8
5*x - 5*2 + 2 = 5x - 8 ==> distribute 5 to x ad -2 using distribution property
5x - 10 + 2 = 5x - 8
-10 + 2 = -8 ==> subtract 5x on both sides
-8 = -8 ==> true
Hence, the equation has infinite solutions since any value of x will result in the equation -8 = -8.
fastt
13. Calculate the compound interest of an annuity due of BD400 paid each 4 months for 6.2 years if the nominal rate is 3% thirdly? (3 Points)
Answers
Therefore, the compound interest of the annuity due of BD 400 paid each 4 months for 6.2 years at a nominal rate of 3% per annum is BD 40,652.17.
Compound interest of an annuity due can be calculated using the formula:A = R * [(1 + i)ⁿ - 1] / i * (1 + i)
whereA = future value of the annuity dueR = regular paymenti = interest raten = number of payments First, we need to calculate the effective rate of interest per period since the nominal rate is given per annum. The effective rate of interest per period is calculated as
:(1 + i/n)^n - 1 = 3/1003/100 = (1 + i/4)^4 - 1
(1 + i/4)^4 = 1.0075i/4 = (1.0075)^(1/4) - 1i = 0.0303So,
the effective rate of interest per 4 months is 3.03%.Next, we can substitute the given values in the formula:
A = BD 400 * [(1 + 0.0303)^(6.2 * 3) - 1] / 0.0303 * (1 + 0.0303)A = BD 400 * [4.227 - 1] / 0.0303 * 1.0303A = BD 400 * 101.63A = BD 40,652.17
For such more question on interest
https://brainly.com/question/25720319
#SPJ8
find the length of MN

Answers
Answer:
The length of MN is 5 cm
Step-by-step explanation:
Add the segment LX, parallel to QP.
Recall the properties of midsegment:
Midsegment is parallel to side,Midsegment is half the length of the parallel side.We have:
Since QL = LR, the point L is midpoint of Q,Since PN = NL, the point N is midpoint of PL,Since LX is parallel to QP, LX is midsegment of ΔPRQ.Find the length of LX:
LX = QP/2 = 20/2 = 10 cmSince QP ║ LX ║ NM, the segment NM is the midsegment of ΔPLX.
Find the length of NM:
NM = LX/2 = 10/2 = 5 cm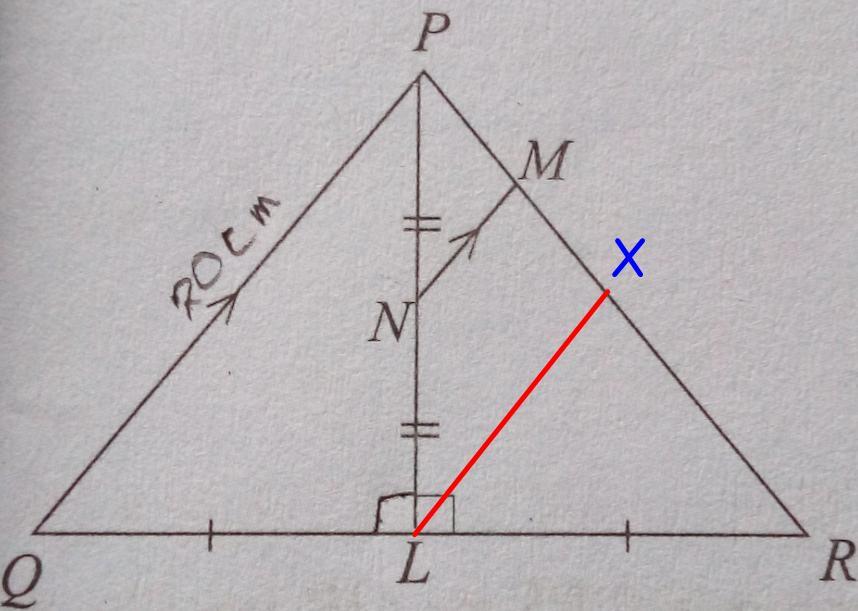
At what point do the lines y = 6x – 18 and
y= 8x – 32 intersect?
Answers
Answer: The lines intersect at the point (7, 24)
Step-by-step explanation:
We have two lines:
y = 6*x - 18
y = 8*x - 32
We want to find the point at which both lines intersect, this means that there is a point (x, y) that belongs to both lines.
This means that we can write:
6*x - 18 = y = 8*x - 32
Because the y-value should be the same for both lines, then we get:
6*x - 18 = 8*x - 32
Now we can solve this for x.
6*x - 18 = 8*x - 32
32 - 18 = 8*x - 6*x
14 = 2*x
14/2 = x = 7
Now we know that the lines intersect at x = 7, replacing this in any of the two equations we can get the y value at which the lines intersect, let's use the first equation:
y = 6*7 - 18 = 24
So the lines intersect at the point (7, 24)
The table shows the amount of dietary fiber in bananas. Use the table to find the constant of proportionality. Express your answer in decimal form
Answers
The table has a constant of proportionality of 0.322
How to determine what is the constant of proportionality?The table that completes the question is added as an attachment
On the table, we have the following points
(x, y) = (9.3, 3)
To determine the constant of proportionality, remove the origin
So, we have
(x, y) = (9.3, 3)
The constant of proportionality of the points is then calculated as
k = y/x
Substitute the known values in the above equation
So, we have
k = 3/9.3
Evaluate the quotient
So, we have
k = 0.322
Hence, the constant of proportionality of the table is 0.322
Read more about constant of proportionality at
brainly.com/question/28413384
#SPJ1

what is the slope and y-intercept for the line y = -2x
Answers
Answer:
slope = - 2, y- intercept = 0
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = - 2x , that is
y = - 2x + 0 ← is in slope- intercept form
with slope m = - 2 and y- intercept c = 0 ( that is the origin )
Do the sides 11 cm, 20 cm, and 4 cm make a triangle? *
Answers
Answer:
No, the two sum of the two shorter sides of a triangle must be greater that the longer side.
Answer: yes it does and It will look something like this
Step-by-step explanation:

indicate whether the following variables are categorical (qualitative) or quantitative. a. model of automobile b. flavor of ice cream c. religious denomination d. testscoreoutof100 e. miles per gallon of gasoline f. top three television networks g. lengthofbirthcontractioninseconds
Answers
The variable a. model of automobile is Qualitative b. flavor of ice cream is Qualitative c. religious denomination is Qualitative d. test score out of 100 is Quantitative e. miles per gallon of gasoline is Quantitative f. top three television networks is Qualitative g. length of birth contraction in seconds is Quantitative.
The Quantitative variable is defined as the variable which takes numerical value. for eg. 2mph, 90 , 34m.
The Qualitative variable is defined as the variable which takes values such as name/label etc. for eg, john , smith , Toyota ,vanilla.
According to the question
VARIABLE CATEGORY CLASSIFIED
a. model of automobile Qualitative on the basis of name
b. flavor of ice cream Qualitative on the basis of name
c. religious denomination Qualitative on the basis of name
d. test score out of 100 Quantitative on the basis of number
e. miles per gallon of gasoline Quantitative on the basis of number
f. top three television networks Qualitative on the basis of name.
g. length of birth contraction Quantitative on the basis of number.
(in seconds)
Therefore , The variable a. model of automobile is Qualitative
b. flavor of ice cream is Qualitative
c. religious denomination is Qualitative
d. test score out of 100 is Quantitative
e. miles per gallon of gasoline is Quantitative
f. top three television networks is Qualitative
g. length of birth contraction in seconds is Quantitative
Learn more about Qualitative & Quantitative variable here https://brainly.com/question/1978633
#SPJ4
Suppose y, ... Yn ~ N(u,02), with y known. Use the non-informative prior p(02) « 1/02. Obtain the sampling distribution (likelihood) and the posterior distribution.
Answers
To obtain the sampling distribution (likelihood) and the posterior distribution for this scenario, we can use Bayesian inference.
The sampling distribution (likelihood) can be represented as:
p(y|u,02) = (1/sqrt(2*pi*02)^n) * exp(-(1/(2*02)) * sum((yi-u)^2))
where y is the observed data, u is the mean of the normal distribution, and 02 is the variance of the normal distribution.
The non-informative prior for 02 can be represented as:
p(02) « 1/02
Using Bayes' theorem, we can obtain the posterior distribution:
p(u,02|y) = p(y|u,02) * p(02) / p(y)
where p(y) is the marginal likelihood. To simplify the calculation, we can integrate out u from the joint distribution:
p(02|y) = (p(y|02) * p(02)) / p(y)
where p(y|02) is the marginal likelihood for 02:
p(y|02) = (1/sqrt(2*pi*02)^n) * exp(-(n-1)/2)
We can then obtain the posterior distribution for 02:
p(02|y) « 1/02 * exp(-(n-1)/2)
This is a gamma distribution with shape parameter (n-1)/2 and scale parameter 1/2. Therefore, the posterior distribution for 02 is:
02|y ~ Gamma((n-1)/2, 1/2)
Learn more about Bayesian inference here:
https://brainly.com/question/31448061
#SPJ11