80 inches of snow over 10 days

Answer:

yep i am very tireddddfdf

Answer:

YEAAA I'm like super tired for no reason, even though I really didn't do anything today :/

Answer:

1.) a. revenue divided by number of posts

b. revenue divided by total number of words

2.) c. no.

Step-by-step explanation:

Answer:

1.

a) Revenue divided by number of posts

b) Revenue divided by total number of words

2.

c) No. The definitions have opposite results.

Answer:

Step-by-step explanation:

v(5v-7)=0

We multiply parentheses

5v^2-7v=0

a = 5; b = -7; c = 0;

Δ = b2-4ac

Δ = -72-4·5·0

Δ = 49

The delta value is higher than zero, so the equation has two solutions

We use following formulas to calculate our solutions:

v1 = −b−√Δ/2a

v2 = -b+√Δ/2a

√Δ = √49 = 7

v1 = -(−7)−7/2*5 = 0/10 = 0

v2 = -(−7)+7/2*5 = 14/10 =  1+2/5

\(\huge\text{Hey there!}\)

\(\huge\textbf{We start off with this current equation:}\)

\(\mathbf{v(5v - 7) = 0}\)

\(\huge\textbf{Solving for the answer to your question:}\)

\(\mathbf{v(5v - 7) = 0}\)

\(\huge\textbf{Convert your current equation to:}\)

\(\mathbf{1v(5v - 7) = 0}\)

\(\huge\textbf{Distribute v or 1 within the parentheses:}\)

\(\mathbf{\rightarrow 1v(5v) + 1v(-7) = 0}\)

\(\mathbf{\rightarrow 5v^2 - 7v = 0}\)

\(\huge\textbf{Factor the left side of the equation:}\)

\(\mathbf{v(5v - 7) = 0}\)

\(\huge\textbf{Fator each of the sides to equal to 0:}\)

\(\mathbf{v = 0\ OR\ as\ in\ 5v - 7 = 0 }\)

\(\huge\textbf{Simplify the current equation above:}\)

\(\mathbf{v = 0\ or\ v = \dfrac{7}{5}}\)

\(\huge\textbf{Thus, the answer should most likely be:}\)

\(\huge\boxed{\mathsf{v = 0\ or\ v = \dfrac{7}{5}}}\huge\checkmark\)

\(\huge\text{Good luck on your assignment \& enjoy your day!}\)

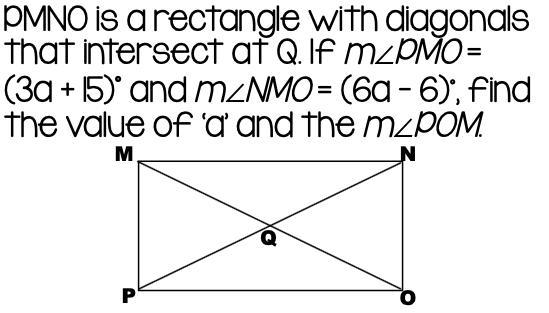
Answer:

Step-by-step explanation:

measure of a = 9 degree

angle POM = 48 degree = angle NMO [ AIA}

HOPE IT HELPS

Answer:

Below

Step-by-step explanation:

We are given that <PMO= (3a+15)° and NMO= (6a-6)°

Notice that the sum of <PMO and <NMO gives a right angle.

● <PMO+<NMO = 90°

● 3a+15+6a-6 = 90

● 9a + 9 = 90

Substruct 9 from both sides

● 9a +9 -9 = 90 -9

● 9a = 81

Divide both sides by 9

● 9a/9 =81/9

● a = 9

So the value of a is 9°

■■■■■■■■■■■■■■■■■■■■■■■■■■

MN and PO are parallel since MNOP is a rectangle.

MO is crossing MN and PO so <POM and < NMO are alternate interior angles wich means that they have the same size.

● <NMO = <POM

● <POM = 6a-6

The value of a is 9°

● <POM = 6*9-6 = 48°

So <POM = 48°

Answer: 13.89 in ==> B

Step-by-step explanation:

A=area of rectangle, l=length, w=width

A=l*w

108.35=7.8*w

108.35/7.8=7.8w/7.8

w=108.35/7.8

w=13.891 ==> w=13.89 in==> B

To solve the equation 4cos^2(x)tan(x) - 2tan(x) = 0 on the interval [0°, 360°), we can use algebraic manipulations and trigonometric identities. Let's simplify the equation step by step:

Start with the given equation: 4cos^2(x)tan(x) - 2tan(x) = 0.

Factor out the common term tan(x): tan(x)(4cos^2(x) - 2) = 0.

Set each factor equal to zero and solve separately:

a) tan(x) = 0:

Since tan(x) is zero at x = 0°, 180°, and 360°, we have x = 0°, 180°, 360° as solutions.

b) 4cos^2(x) - 2 = 0:

Add 2 to both sides: 4cos^2(x) = 2.

Divide by 4: cos^2(x) = 1/2.

Take the square root: cos(x) = ±√(1/2).

To find the values of x in the interval [0°, 360°), we need to consider both the positive and negative square root:

cos(x) = √(1/2):

x = 45°, 315° (since cos(45°) = cos(315°) = 1/√2)

cos(x) = -√(1/2):

x = 135°, 225° (since cos(135°) = cos(225°) = -1/√2)

Therefore, the solutions to the equation 4cos^2(x)tan(x) - 2tan(x) = 0 on the interval [0°, 360°) are: x = 0°, 45°, 135°, 180°, 225°, 315°, and 360°.

Learn more about equation from

https://brainly.com/question/17145398

#SPJ11

we can set up the equation: 5x + x = £468, representing the total amount spent plus the amount saved. Therefore, Sam spent £390 based on the given ratio of 5:1. Sam spent £390.

Let's assume the amount Sam spent is 5x and the amount he saved is x, based on the given ratio of 5:1. We know that the total amount Sam had was £468.

According to the given information, we can set up the equation: 5x + x = £468, representing the total amount spent plus the amount saved.

Combining like terms, we get: 6x = £468.

To solve for x, we divide both sides of the equation by 6: x = £468 / 6.

Evaluating the expression, we find: x = £78.

Since x represents the amount saved, Sam spent 5x, which is 5 * £78 = £390.

Therefore, Sam spent £390 based on the given ratio of 5:1.\

Learn more about expression here:

https://brainly.com/question/28170201

#SPJ11

The given function as;

f(x) = x² - 8x + 3

f(x + h) , susbtitute x = x + h in the given expression as;

f(x+h) = (x+h)² - 8(x+h) + 3

f(x+h) = (x² + h² + 2xh) -8x - 8h + 3

f(x+h) = x² + h² + 2xh - 8x - 8h + 3

Now substitute the value of f(x+h) in the expression as;

Answer : 2x + h - 8

.........

The equation of the linear function represented by the table below in slope-intercept form is y = 7x + 4

The equation of a line in point-slope form is expressed as y = mx + b

where

m is the slope

b is the intercept

Using the coordinate points (0,4) and (1, 11)

Slope = 11-4/1-0

slope = 7

The y-intercept is at the point (0,4)

Determine the equation

y = mx + b

y = 7x + 4

Hence the equation of the linear function represented by the table below in slope-intercept form is y = 7x + 4

Learn more on equation of a line here: https://brainly.com/question/18831322

#SPJ1

True.

if y is not the zero vector, then there exists a non-zero vector v in the original vector space that is orthogonal to y.

If y is in a subspace W as well as its orthogonal complement Wâ¥, then y is orthogonal to every vector in W as well as every vector in Wâ¥. Since W and W⥠are complements, every vector in the original vector space can be written uniquely as the sum of a vector in W and a vector in Wâ¥. Since y is orthogonal to every vector in W and every vector in Wâ¥, it must be orthogonal to every vector in the original vector space.

Therefore, if y is not the zero vector, then there exists a non-zero vector v in the original vector space that is orthogonal to y. But then v would belong to both W and Wâ¥, which is impossible since W and W⥠are orthogonal complements and their intersection is only the zero vector.

Hence, it follows that if y is in a subspace W as well as its orthogonal complement Wâ¥, then y must be the zero vector.

Visit to know more about Vector:-

brainly.com/question/25705666

#SPJ11

Answer:

4 plants

Step-by-step explanation:

convert the capacity of the watering can to millimeters

1L = 1000 milliliters

1 x 1000 = 1000 millimeters

Plants that can be watered = capacity of the watering can / amount of water a plant needs

1000 / 250 = 4 plants

A pyramid has a volume of 173.88 ft3, is 10.5 feet tall, and has a rectangle-shaped base that is 7.2 feet by 6.9 feet in size.

A rectangular pyramid has five faces altogether. Its rectangular base serves as one face, and the remaining four faces are all triangular in shape. All of the triangles in this are congruent with the triangle to the opposite. The formula for a pyramid's total surface area is 12 pl + B, where p is the base's perimeter, l is the pyramid's slant height, and B is the base's area.

The volume of a rectangular pyramid is found using the formula Volume = 1/3 × base area × height.

height is 10.5 feet

dimensions of 7.2 feet by 6.9 feet.

volume = L× B × H /3

volume = 7.2·6.9·10.5 /3

volume = 173.88ft³.

To know more about pyramid visit:-

https://brainly.com/question/23857979

#SPJ1

a) For a random sample of 5 students, the probability of exactly two students being mature is: 0.279

b) For a random sample of 7 students, the probability of exactly two students being mature is: 0.302

For a university where 22% of the students enrolled are 'mature' (age 21 or over), the probability of exactly two students being mature in a random sample of 5 students is approximately 0.279. Similarly, the probability of exactly two students being mature in a random sample of 7 students is approximately 0.302.

To calculate the probability of exactly two students being mature in a random sample, we can use the binomial probability formula:

P(X=k) = \(^nC_{k} * p^k * (1-p)^{(n-k)}\)

Where:

P(X=k) is the probability of having exactly k successes (in this case, exactly two mature students),

(\(^nC_{k}\)) represents the number of combinations of selecting k items from a set of n items,

p is the probability of a single success (the probability of a student being mature),

(1-p) is the probability of a single failure (the probability of a student not being mature),

n is the sample size.

a) For a random sample of 5 students, the probability of exactly two students being mature is:

P(X=2) = (\(^5C_2\)) * (0.22)² * (0.78)³ ≈ 0.279

b) For a random sample of 7 students, the probability of exactly two students being mature is:

P(X=2) = (\(^7C_2\)) * (0.22)² * (0.78)⁵ ≈ 0.302

These calculations assume that each student's maturity status is independent of the others and that the sample is taken randomly from the enrollment register.

To learn more about binomial probability formula visit:

brainly.com/question/30764478

#SPJ11

The area of the shaded sector is 4π square units.

To find the area of the shaded sector, we need to calculate the central angle formed by the sector. In this case, we are given that the angle JIK is 90 degrees, which means it forms a quarter of a full circle.

Since a full circle has 360 degrees, the central angle of the shaded sector is 90 degrees.

Next, we need to determine the radius of the circle. The line segment IJ represents the radius of the circle, and it is given as 4 units.

The formula to calculate the area of a sector is A = (θ/360) * π * r², where θ is the central angle and r is the radius of the circle.

Plugging in the values, we have A = (90/360) * π * 4².

Simplifying, A = (1/4) * π * 16.

Further simplifying, A = (1/4) * π * 16.

Canceling out the common factors, A = π * 4.

Hence, the area of the shaded sector is 4π square units.

Therefore, the area of the shaded sector, expressed as a fraction times π, is 4π/1.

In summary, the area of the shaded sector is 4π square units, or 4π/1 when expressed as a fraction times π.

For more such questions on area, click on:

https://brainly.com/question/25292087

#SPJ8

=======================================================

If a < 7, then |a-7| = -(a-7) = -a+7 based on how absolute value functions are constructed. We're using the idea that

\(|x-k| = \begin{cases}x-k \ \text{ if } \ x \ge k\\ -(x-k) \ \text{ if } \ x < k\end{cases}\)

Also, if a < 7, then |a-9| = -(a-9) = -a+9. This is true whenever 'a' is less than 9 for similar reasoning as above.

---------

So we have,

|a-7| - |a-9| = -a+7 - (-a+9) = -a+7+a-9 = -2

As long as a < 7, the result of |a-7| - |a-9| will always be -2.

---------

As an example, let's say a = 0

|a-7| - |a-9| = |0-7| - |0-9|

|a-7| - |a-9| = |-7| - |-9|

|a-7| - |a-9| = 7 - 9

|a-7| - |a-9| = -2

I recommend you try out other values of 'a' to see if you get -2 or not. Of course only pick values that are smaller than 7.

Answer:

h = 13ft

Step-by-step explanation:

We can assume that the triangles are similar, so:

5 ft is to 26 ft as 2.5 ft is to h ft.

Which can be set up like this:

\(\frac{5}{2.5}=\frac{26}{h}\)

We can cross multiply:

5h = (2.5) (26)

5h = 65

h = 13ft

Step-by-step explanation:

the patern (3n - 1) is incorrect,

the correct pattern should be

Tn = n² + 1

The side of the square equals half the minor axis of the ellipse.

To show that the side of the square is half the minor axis of the ellipse, we must prove that the angles of the ellipses and the squares are congruent. To do this, we must first draw in the diagonals of the square, which will form two additional isosceles triangles.

Since the ellipses are perpendicular, the angles of the ellipses and the squares will be the same. Since the angles of the isosceles triangles are equal, the side of the square must be equal to half of the minor axis of the ellipse. Therefore, the side of the square is equal to half of the minor axis of the ellipse.

For more questions like Minor axis click the link below:

https://brainly.com/question/29054958

#SPJ4

Using the slope formula, it is found that the value of j is 12.

The slope is the ratio of the vertical changes to the horizontal changes between two points of the line. The equation of the straight line has its slope and given point.

If we have a non-vertical line that passes through any point(x1, y1) has gradient m. then general point (x, y) must satisfy the equation

m = ( y₂ - y₁ ) / ( x₂ - x₁ )

Given;

A line with a slope of -1/10 passes through the points (-2,6) and (j,5).

Now,

m = ( y₂ - y₁ ) / ( x₂ - x₁ )

-1/10= 5-6/j+2

-1/10= -1/j+2

10=j+2

j=12

Therefore, by the given slope j will be 12.

Learn more about slope here:

https://brainly.com/question/2503591

#SPJ9

State the null and alternative hypotheses, determine the level of significance, Calculate the test statistic also determine the critical value.

Step 1: Express the invalid and elective speculations,

The invalid speculation is that the change of halting distances on wet asphalt is equivalent to or not exactly the fluctuation of halting distances on dry asphalt.

H0: σ2(wet) ≤ σ2(dry)

The other possibility is that the variance of stopping distances on wet pavement is greater than that on dry pavement.

Ha: σ2(wet) > σ2(dry)

Step 2: Choose the appropriate test and determine the significance level,

The level of significance is 5%. Since we are comparing two variances of normally distributed populations, we will use the F-test.

Step 3: Calculate the test statistic,

The F-test measurement is determined as the proportion of the example differences:

F = s2(wet)/s2(dry)

where s2(wet) and s2(dry) are the sample variances of stopping distances on wet and dry pavement, respectively.

F = 32²/16² = 4

Step 4: Determine the critical value

The critical value for the F-test with 15 and 15 degrees of freedom (16-1 and 16-1) at a 5% level of significance is 2.54 (from F-tables).

Step 5: Settle on a choice and decipher the outcomes,

Since the calculated F-value of 4 is greater than the critical value of 2.54, we reject the null hypothesis. We can conclude that the variance of stopping distances on wet pavement is greater than the variance of stopping distances on dry pavement.

To know more about driving safety, visit:

https://brainly.com/question/1071840

#SPJ1

The transformation of System A into System B is:

Equation [A2]+ Equation [A 1] → Equation [B 1]"

The correct answer choice is option D

How can we transform System A into System B?

To transform System A into System B as 1 × Equation [A2] + Equation [A1]→ Equation [B1] and 1 × Equation [A2] → Equation [B2].

System A:

-3x + 4y = -23 [A1]

7x - 2y = -5 [A2]

Multiply equation [A2] by 2

14x - 4y = -10

Add the equation to equation [A1]

14x - 4y = -10

-3x + 4y = -23 [A1]

11x = -33 [B1]

Multiply equation [A2] by 1

7x - 2y = -5 ....[B2]

So therefore, it can be deduced from the step-by-step explanation above that System A is ultimately transformed into System B as 1 × Equation [A2] + Equation [A1]→ Equation [B1] and 1 × Equation [A2] → Equation [B2].

The complete image is attached.

Read more equations:

brainly.com/question/13763238

#SPJ1

Given:

The graph of a parabola.

To find:

The equation of the parabola.

Solution:

From the given graph, it is clear that the vertex of the parabola is at point (0,0) and it is a horizontal parabola.

The general equation of a horizontal parabola is:

\(x=ay^2\)

Where, a is a constant.

If a<0, then the parabola opens left and if a>0, then the parabola opens right.

Equations in options B and D are of the form \(x=ay^2\) but a<0 in option B and a>0 in option D.

In the given graph the parabola opens right, so the value of a mus be a positive number. So, the required equation is:

\(x=\dfrac{1}{6}y^2\)

Therefore, the correct option is D.

1: 8 faces and 9 with the base 9 vertices and 16 edges

2: 3 faces and 5 with the bases 6 vertices and 9 edges

3: 3 faces and 4 with the base 4 vertices and 6 edges

Hope this can help you.

Answer:

1: 8 faces and 9 with the base 9 vertices and 16 edges

2: 3 faces and 5 with the bases 6 vertices and 9 edges

3: 3 faces and 4 with the base 4 vertices and 6 edges

Step-by-step explanation:

Answer:

Find the values of x and y

X =60

Y=60

60°

Answer:

x = 20

Step-by-step explanation:

Hello!

Solve for x by isolating the variable.

The value of x is 20.

Performing the calculation \(\frac{0.32610}{1.830}\) and rounding the answer to the proper number of significant figures gives us approximately 0.178.

To explain the calculation further, we divide 0.32610 by 1.830. The division results in a quotient of 0.1781967213. However, since we need to round the answer to the proper number of significant figures, we look at the least precise number in the given values, which is 1.830 with four significant figures. Therefore, we round the quotient to three significant figures, giving us approximately 0.178 as the final result.

Significant figures are used to indicate the precision of a number or measurement. They include all the certain digits in a number and the first uncertain or estimated digit. When performing mathematical operations, it's important to consider significant figures and round the final result accordingly to maintain accuracy and proper representation of precision.

In this case, the division yields a result with ten significant figures, but we round it to three significant figures since that is the least precise value among the given numbers. This ensures that the answer reflects the appropriate level of precision and adheres to the rules of significant figures.

know more about proper number :brainly.com/question/28882489

#SPJ11

Performing the calculation \(\frac{0.32610}{1.830}\) and rounding the answer to the proper number of significant figures gives us approximately 0.178.

To explain the calculation further, we divide 0.32610 by 1.830. The division results in a quotient of 0.1781967213. However, since we need to round the answer to the proper number of significant figures, we look at the least precise number in the given values, which is 1.830 with four significant figures. Therefore, we round the quotient to three significant figures, giving us approximately 0.178 as the final result.

Significant figures are used to indicate the precision of a number or measurement. They include all the certain digits in a number and the first uncertain or estimated digit. When performing mathematical operations, it's important to consider significant figures and round the final result accordingly to maintain accuracy and proper representation of precision.

In this case, the division yields a result with ten significant figures, but we round it to three significant figures since that is the least precise value among the given numbers. This ensures that the answer reflects the appropriate level of precision and adheres to the rules of significant figures.

know more about proper number :brainly.com/question/28882489

#SPJ11

There are two real number solutions for x2 − 5x + 7 = 0: x = 2 and x = 7.

1. x2 − 5x + 7 = 0

2. (x - 2)(x - 7) = 0

3. x = 2 or x = 7

When solving for the real number solutions of x2 − 5x + 7 = 0, we first need to factor the equation into two linear terms: (x - 2)(x - 7) = 0. From here, we can use the Zero Product Property to determine that x = 2 and x = 7 are the two real number solutions of this equation. This means that when x is equal to 2 or 7, the equation will equal 0 and all other values of x will result in a non-zero answer. Therefore, the only two real number solutions of x2 − 5x + 7 = 0 are x = 2 and x = 7.

Learn more about real number here

https://brainly.com/question/10547079

#SPJ4

The cost of pendant of the three necklaces owned by Joe is $9.90.

For the given question;

There are three  identical necklaces, each having beads and a pendant owned by Joe.

Total cost (beads and pendant for all 3 necklaces) = $15.60.

Total cost for brads = $5.70.

Thus, the cost of pendant = Total cost - Cost of beads

Cost of pendant = $15.60 - $5.70.

Cost of pendant = $9.90

Thus, the cost of pendant of the three necklaces owned by Joe is $9.90.

To know more about the subtraction, here

https://brainly.com/question/25421984

#SPJ1

a. The 99% confidence interval for μ is approximately (5.536%, 8.264%).

b. The alternative hypothesis (Ha) is: The average compensation of all CEOs increased in 2021.

c. The test statistic value is calculated using the formula:

Z = (X - μ) / (σ / sqrt(n))

d.  if the p-value is less than the significance level (α = 0.01), we would reject the null hypothesis and conclude that there is strong evidence that the average compensation of all CEOs increased in 2021.

a. To construct the 99% confidence interval for the population mean (μ), we can use the formula:

CI = X ± Z * (σ / sqrt(n))

where X is the sample mean, Z is the Z-score corresponding to the desired confidence level (99% in this case), σ is the population standard deviation, and n is the sample size.

Given:

X = 6.9%

σ = 5.5%

n = 104

Confidence level = 99%

First, we need to find the Z-score corresponding to a 99% confidence level. Using a Z-table or statistical software, the Z-score is approximately 2.576.

Now we can plug in the values into the formula:

CI = 6.9% ± 2.576 * (5.5% / sqrt(104))

Calculating the values:

CI = 6.9% ± 2.576 * (0.5295%)

= 6.9% ± 1.364%

The 99% confidence interval for μ is approximately (5.536%, 8.264%).

b. The null hypothesis (H0) for testing whether the average compensation of all CEOs increased in 2021 is: The average compensation of all CEOs remained the same or decreased in 2021.

The alternative hypothesis (Ha) is: The average compensation of all CEOs increased in 2021.

c. To determine the test statistic, we need to know the sample mean, population standard deviation, sample size, and the distribution of the population. Since the population standard deviation (σ) is known and the sample size is relatively large (n > 30), we can use the Z-test.

The test statistic value is calculated using the formula:

Z = (X - μ) / (σ / sqrt(n))

where X is the sample mean, μ is the hypothesized population mean under the null hypothesis, σ is the population standard deviation, and n is the sample size.

However, the value of the test statistic is not provided in the given information.

d. To determine if the study gives strong evidence that the average compensation of all CEOs went up, we compare the p-value to the significance level (α).

Since the p-value is not given in the information provided, we cannot make a direct conclusion. However, if the p-value is less than the significance level (α = 0.01), we would reject the null hypothesis and conclude that there is strong evidence that the average compensation of all CEOs increased in 2021.

Learn more about   interval  from

https://brainly.com/question/30460486

#SPJ11