3/(2x-1)+4=6x/(2x-1)
X=?
Answers
Explanation:
3/(2x-1) + 4 = 6x/(2x-1)
3/2x-1 + 4(2x-1)/2x-1 = 6x/2x-1
3 + 8x -4 = 6x
8x -1 = 6x
2x = 1
x = 1/2
Related Questions
Sort the angles as acute, right, obtuse, or straight.

Answers
The top angle is right (90 degrees, kinda looks like a bent elbow).
The 2nd is acute (smaller than 90, kind of 'cute' bc it's small).
The 3rd is obtuse (greater than 90, I have nothing corny to say, sorry).
4th is acute.
5th is straight because it's a straight line.
6th is also obtuse.
Have a good day :)
What is the remainder when the following polynomial division is performed? Place the answer in the proper location of the gird. Do not include parentheses in your answer.

Answers
The remainder of the polynomial division \(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)}\) is 2y²
How to determine the remainder of the polynomial divisionFrom the question, we have the following parameters that can be used in our computation:
\(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)}\)
When the numerator is expanded, we have
\(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)} = \frac{(y - 1)(y^3 + 1) + 2y^2}{y^3 + 1}\)
Split the expanded expression
\(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)} = \frac{(y - 1)(y^3 + 1)}{y^3 + 1} + \frac{2y^2}{y^3 + 1}\)
Evaluate
\(\frac{\left(y^4-y^3+2y^2+y-1\right)}{\left(y^3+1\right)} = y - 1 + \frac{2y^2}{y^3 + 1}\)
From the above, we have
Quotient = y - 1
Remainder = 2y²
Hence, the remainder of the polynomial division is 2y²
Read more about polynomial division at
https://brainly.com/question/7693326
#SPJ1
What is the length of AC?

Answers
So the answer is 9cm
What is the coefficients and Constants for 5x-10
Answers
Answer:
coefficient
5
constant
-10
Step-by-step explanation:
5x-10
The coefficient is the number in front of the variable
5
The constant is the number alone
-10
Three baseball players are playing catch. Jessica is directly south of Aaron and directly west of Mike. Jessica and Mike are 8 meters apart and Mike and Aaron are 10 meters apart, How far apart are Jessica and Aaron?
Answers
Answer:
6 m
Step-by-step explanation:
The diagrammatic illustration of the problem. Is attached
The diaabcw between Aaron and Jessica can be obtained using Pythagoras :
d = √(10² - 8²)
d = √100 - 64
d = √36
d = 6

Need Help!!!! A pre-image has coordinates J(3, -6) and K(-1, -2). The image has coordinates J'(6, 3) and K'(2, -1). Describe the clockwise rotational path of the line segment.
Answers
After considering the given data we conclude that the clockwise rotational path of the line segment is a rotation of -59.04 degrees about the point (-6, -1).
We have to evaluate the center and angle of rotation to explain the clockwise rotation of the line segment.
So in the first step, we can evaluate the midpoint of the line segment JK and the midpoint of the line segment J'K'. we can calculate the vector connecting the midpoint of JK to the midpoint of J'K'. This vector is (4-1, 1-(-4) = (3,5)
The center of rotation is the point that is equidistant from the midpoints of JK and J'K'. We can evaluate this point by finding the perpendicular bisector of the line segment connecting the midpoints.
The slope of this line is the negative reciprocal of the slope of the vector we just found, which is -3/5. We can apply the midpoint formula and the point-slope formula to evaluate the equation of the perpendicular bisector:
Midpoint of JK: (1, -4)
Midpoint of J'K': (4, 1)
The slope of the vector: 3/5
(x₁ + x₂)/2, (y₁ + y₂) /2
Point-slope formula: y - y₁ = m(x - x₁)
Perpendicular bisector: y - (-4) = (- 3/5)(x - 1)
Applying simplification , we get: y = (- 3/5)x - 1.2
To evaluate the center of rotation, we need to find the intersection point of the perpendicular bisector and the line passing through the midpoints of JK and J'K'. This line has slope ( 3 - (4)) /(4 - 1) = 7/3 and passes through the point (4, 1). Applying the point-slope formula, we can evaluate its equation:
y - 1 = (7/3)( x - 4)
Apply simplification , we get: y = (7/3)x - 17/3
To evaluate the intersection point, we can solve the system of equations:
y =(- 3/5)x - 1.2 = (7/3)x - 17/3
Evaluating for x and y, we get x = -6 and y = -1.
Therefore, the center of rotation is (-6, -1).
√( 4 - 1)² + ( 1 - ( - 4))²) = 5√(2)
Distance between image points and center of rotation
√( ( 6 - (-6))² + ( 3 - (-1))² = 13
The ratio of these distances gives us the scale factor of the transformation, which is 13/√2).
The angle of rotation is negative as the image moves clockwise direction. We can apply the inverse tangent function to find the angle of the vector connecting the midpoint of JK to the midpoint of J'K':
Angle of vector: arctan(5/3) = 59.04 degrees
Therefore, the clockwise rotational path of the line segment is a rotation of -59.04 degrees about the point (-6, -1).
To learn more about midpoint formula
https://brainly.com/question/30276996
#SPJ1
Kerry invited 23 friends to his pool party. They played a game where everyone had to separate into groups. Each group had the same number of children.The game could not be played with all 24 children in one group and each group had to have more than two children. Which of the following are ways that they could divide into groups? Choose all that apply.
Answers
Answer:
24:
6 of 4
or
8 of 3
Step-by-step explanation:
6x4=24
8x3=24
(10 points) Consider the initial value problem y′+3y=9t,y(0)=7. Take the Laplace transform of both sides of the given differential equation to create the corresponding algebraic equation. Denote the Laplace transform of y(t) by Y(s). Do not move any terms from one side of the equation to the other (until you get to part (b) below). = help (formulas) Solve your equation for Y(s). Y(s)=L{y(t)}=
Answers
Answer:
The solution
\(Y (s) = 9( -1 +3 t + e^{-3 t} ) + 7 e ^{-3 t}\)
Step-by-step explanation:
Explanation:-
Consider the initial value problem y′+3 y=9 t,y(0)=7
Step(i):-
Given differential problem
y′+3 y=9 t
Take the Laplace transform of both sides of the differential equation
L( y′+3 y) = L(9 t)
Using Formula Transform of derivatives
L(y¹(t)) = s y⁻(s)-y(0)
By using Laplace transform formula
\(L(t) = \frac{1}{S^{2} }\)
Step(ii):-
Given
L( y′(t)) + 3 L (y(t)) = 9 L( t)
\(s y^{-} (s) - y(0) + 3y^{-}(s) = \frac{9}{s^{2} }\)
\(s y^{-} (s) - 7 + 3y^{-}(s) = \frac{9}{s^{2} }\)
Taking common y⁻(s) and simplification, we get
\(( s + 3)y^{-}(s) = \frac{9}{s^{2} }+7\)
\(y^{-}(s) = \frac{9}{s^{2} (s+3}+\frac{7}{s+3}\)
Step(iii):-
By using partial fractions , we get
\(\frac{9}{s^{2} (s+3} = \frac{A}{s} + \frac{B}{s^{2} } + \frac{C}{s+3}\)
\(\frac{9}{s^{2} (s+3} = \frac{As(s+3)+B(s+3)+Cs^{2} }{s^{2} (s+3)}\)
On simplification we get
9 = A s(s+3) +B(s+3) +C(s²) ...(i)
Put s =0 in equation(i)
9 = B(0+3)
B = 9/3 = 3
Put s = -3 in equation(i)
9 = C(-3)²
C = 1
Given Equation 9 = A s(s+3) +B(s+3) +C(s²) ...(i)
Comparing 'S²' coefficient on both sides, we get
9 = A s²+3 A s +B(s)+3 B +C(s²)
0 = A + C
put C=1 , becomes A = -1
\(\frac{9}{s^{2} (s+3} = \frac{-1}{s} + \frac{3}{s^{2} } + \frac{1}{s+3}\)
Step(iv):-
\(y^{-}(s) = \frac{9}{s^{2} (s+3}+\frac{7}{s+3}\)
\(y^{-}(s) =9( \frac{-1}{s} + \frac{3}{s^{2} } + \frac{1}{s+3}) + \frac{7}{s+3}\)
Applying inverse Laplace transform on both sides
\(L^{-1} (y^{-}(s) ) =L^{-1} (9( \frac{-1}{s}) + L^{-1} (\frac{3}{s^{2} }) + L^{-1} (\frac{1}{s+3}) )+ L^{-1} (\frac{7}{s+3})\)
By using inverse Laplace transform
\(L^{-1} (\frac{1}{s} ) =1\)
\(L^{-1} (\frac{1}{s^{2} } ) = \frac{t}{1!}\)
\(L^{-1} (\frac{1}{s+a} ) =e^{-at}\)
Final answer:-
Now the solution , we get
\(Y (s) = 9( -1 +3 t + e^{-3 t} ) + 7 e ^{-3t}\)
30p+2
can you please answer
Answers
Answer:
2(15p+1)
Step-by-step explanation:
hope this helps
Which of the following transformations shows that figure C is congruent to figure C'?A.reflection in the x-axis
B.rotation 90 counterclockwise about the origin
C.rotation 180 counterclockwise about the origin
D.rotation 270 counterclockwise about the origin
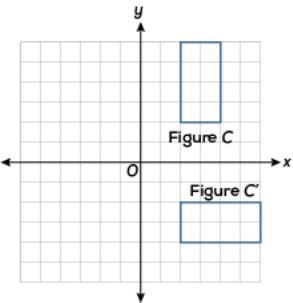
Answers
Answer: D.rotation 270 counterclockwise about the origin
Step-by-step explanation:
100 Points! Algebra question. Photo attached. Find the amplitude, if it exists, and period of the function. Then graph the function. Thank you!

Answers
hello
the answer to the question is:
y = a cot(bx – c) + d
a = 1, b = 1/2, c = 0
the midline is y = d, so y = 0
the vertical stretch is 1, so label the y-axis so the inflection point of the curve is 1 above the midline, and the other inflection point is 1 below the midline
the period is:
T = π/b ----> T = 2π
the phase shift is:
PS = c/b ----> PS = 0
and also, there's no amplitude for tangent and cotangent, there is only the vertical stretch that takes the place of an amplitude

Answer:
amplitude does not exist. period = 2π (360°)
Step-by-step explanation:
there is no amplitude for tan θ or cot θ, since there is no limit up or down (positive/negative infinity).
period for cot θ is π (180°)
period for cot 1/2 θ is 2π (360°)

Select the correct answer from each drop-down menu. y 11 10 Weight (kilograms) 9 00 7 CO 5 3 2 1 5 6 7 Age (months) The scatter plot shows the weight of a child each month. 1 rights reserved 2 3 4 The birth weight of the child is V X 8 9 10 11 kilograms. The child gains an average of per month. Select the correct answer from each drop - down menu . y 11 10 Weight ( kilograms ) 9 00 7 CO 5 3 2 1 5 6 7 Age ( months ) The scatter plot shows the weight of a child each month . 1 rights reserved 2 3 4 The birth weight of the child is (blank) kilograms . The child gains an average of(blank) per month .

Answers
Answer:
its wrong answer and question
The rectangular foor of a classrom is 30 feet in length and 24 feet in width. A scale drawing of the floor has a length of 5 inches. What is the perimeter, in inches, of the floor in the scale drawing?
Answers
The required perimeter of the scale drawing is given as 18 inches.
Given that,
The rectangular floor of a classroom is 30 feet in length and 24 feet in width. A scale drawing of the floor has a length of 5 inches. The perimeter, in inches, of the floor in the scale drawing, is to be determined.
Perimeter is the measure of the figure on its circumference.
Here,
According to the question,
L = 30 feet, W = 24 feet,
for Scaled drawing
l = 5 inch, w = x
Now,
30/5 = 24 / x
6 = 24 / x
x = 24 {1/6}
x = 4,
So the width of the scale drawing is 4 inches,
perimeter of the scaled drawing = 2[l + w]
= 2 [5 + 4] = 18 inches
Thus, the required perimeter of the scale drawing is given as 18 inches.
learn more about perimeter here:
brainly.com/question/6465134
#SPJ1
CAN SOMEONE HELP ME PLEASE (ASAP)

Answers
Answer:
what do you need help with
Step-by-step explanation:
what is the answer of 5ax +8ax+6ax=?
Answers
All have ax included so add the numbers together.
5ax + 8ax + 6ax = 19ax
If it’s mere addition then the answer should be “19ax”.
Lmk if I ryt!!
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
9x^8 y^2 - 6x^3 y^4 / 3xy
simplified

Answers
Answer:
None of the choices are correct
Stefofp-by-step explanation:
Simplify the following:
(-6 x^3 y^4 + 9 x^8 y^2)/(3 x y)
Factor 3 x^3 y^2 out of -6 x^3 y^4 + 9 x^8 y^2:
(3 x^3 y^2 (-2 y^2 + 3 x^5))/(3 x y)
(3 x^3 y^2 (-2 y^2 + 3 x^5))/(3 x y) = 3/3×(x^3 y^2 (-2 y^2 + 3 x^5))/(x y) = (x^3 y^2 (-2 y^2 + 3 x^5))/(x y):
(x^3 y^2 (-2 y^2 + 3 x^5))/(x y)
Combine powers. (x^3 y^2 (-2 y^2 + 3 x^5))/(x y) = x^(3 - 1) y^(2 - 1) (-2 y^2 + 3 x^5):
x^(3 - 1) y^(2 - 1) (-2 y^2 + 3 x^5)
3 - 1 = 2:
x^2 y^(2 - 1) (-2 y^2 + 3 x^5)
2 - 1 = 1:
Answer: x^2 y (-2 y^2 + 3 x^5)
The manager of a fast-food restaurant determines that the average time that her customers wait for service is 2.5 minutes. (a) Find the probability that a customer has to wait more than 4 minutes. (Round your answer to three decimal places.)
Answers
Answer:
0.758
explaination
using poisson distribution
0.08208+0.2052+0.2565+0.2138
0 .758
A local screen-printing company sells T-shirts at various prices, in dollars, depending upon how many T-shirts are bought at the time. The piecewise function below represents their pricing structure, where n is the number of T-shirts purchased. The school volleyball team purchased 20 shirts.
How much did the volleyball team spend on shirts?
$480
$180
$220
$260
Answers
Answer:
i think it’s 260 too^^
Step-by-step explanation:
The total Amount Spent by the volleyball team spend on shirts from the given piecewise function is; $260
How to work with Piecewise Function?
From the given piecewise function, we see that;
y = {13n, 0 < n ≤ 20
y = {11n, 20 < n ≤ 50
y = {9n, n > 50
We are told that the volleyball team purchased 20 shirts.
From the first piecewise function, we can deduce that;
Amount Spent = 13n = 13 * 20
Amount Spent = $260
Read more about Piecewise function at; https://brainly.com/question/4494373
Two sides of a triangle measure 8 cm and 15 cm. Which could be the length of the third side?
Answers
Answer:
I believe the thirds length could be 17 cm
Step-by-step explanation:
Answer:
17
Step-by-step explanation:
8² + 15² = y²
64 + 225 = y²
y² = 289
√y² = √289
y = 17
I need to find the value of x?

Answers
Answer:
x=20
Step-by-step explanation:
120=6x
120/6=6x/6
20=x
factorise:x^3-(y-z)^3
Answers
The factorized form of \(x^3 - (y - z)^3\ is \ (x - y + z)(x^2 - xy + 2xz + yz - 2z^2).\)
The Factorization is derived from the application of a mathematical identity. As an AI language model, the information provided is generated based on existing knowledge and formulas.
The given expression is \(x^3 - (y - z)^3.\)To factorize it, the difference of cubes, which states that a^3 - b^3 can be factorized as\((a - b)(a^2 + ab + b^2).\)
Applying this identity to our expression, we have:
\(x^3 - (y - z)^3 = (x - (y - z))((x - (y - z))^2 + (x - (y - z))(y - z) + (y - z)^2)\)
Simplifying further, we get:
\(= (x - y + z)(x^2 - 2xy + 2xz - y^2 + 2yz - z^2 + xy - y^2 + yz - z^2 + y^2 - 2yz + z^2)\\= (x - y + z)(x^2 - 2xy + xy + 2xz + yz - 2yz - y^2 + y^2 - y^2 + 2yz - 2z^2 + y^2 - z^2 + z^2)\\= (x - y + z)(x^2 - xy + 2xz + yz - 2z^2)\)
So, the factorized form of \(x^3 - (y - z)^3 \ is\ (x - y + z)(x^2 - xy + 2xz + yz - 2z^2).\)
the above factorization is derived from the application of a mathematical identity.
To know more about factorized .
https://brainly.com/question/14268870
#SPJ11
Put the lowest number on left, 5/6, 2/3, 1/2
Answers
Answer:
Step-by-step explanation:
1/2 , 2/3 , 5/6
5. En una investigación hecha a un grupo de 100 estudiantes, la cantidad de personas que estudian idiomas fueron las siguientes: español, 28; alemán, 30; y francés, 42; español y alemán, 8; español y francés 10; alemán y francés 5; los tres idiomas 3. a) ¿Cuántos alumnos no estudian ningún idioma?
Answers
There are 20 students who do not study any language.
To determine the number of students who do not study any language, we need to subtract the total number of students who study at least one language from the total number of students in the group.
Given the information provided, we can use the principle of inclusion-exclusion to calculate the number of students who study at least one language.
Using the inclusion-exclusion principle, we can calculate the number of students who study at least one language as follows:
Students studying at least one language = Students studying Spanish + Students studying German + Students studying French - Students studying Spanish and German - Students studying Spanish and French - Students studying German and French + Students studying all three languages
Substituting the given values from the question:
Students studying at least one language = 28 + 30 + 42 - 8 - 10 - 5 + 3
Students studying at least one language = 80
Now, we can calculate the number of students who do not study any language:
Students not studying any language = Total number of students - Students studying at least one language
Students not studying any language = 100 - 80
Students not studying any language = 20
20 students do not study any languages, as a result.
for such more question on total number
https://brainly.com/question/19079438
#SPJ8
5/6 x 12 in simplest form?
Answers
Answer:
10
Step-by-step explanation:
Answer:
The answer is 10
Step-by-step explanation:
Los organizadores de la Feria de Alimentos colocan un contenedor de agua que mide 2,76 metros de largo, por 23,5 decímetros de ancho y por 196 centímetros de alto. ¿Cuál es el volumen del contenedor? Expresa la respuesta en metros cúbicos con aproximación a centésimos.
Answers
The volume of the container is approximately 12.9516 cubic meters when rounded to the nearest hundredth.
To find the volume of the container, we need to multiply its length, width, and height. Let's convert the given measurements to meters to ensure consistent units.
The length of the container is 2.76 meters.
The width of the container is 23.5 decimeters, which is equal to 2.35 meters (since 1 decimeter = 0.1 meters).
The height of the container is 196 centimeters, which is equal to 1.96 meters (since 1 meter = 100 centimeters).
Now we can calculate the volume of the container:
Volume = Length × Width × Height
Volume = 2.76 meters × 2.35 meters × 1.96 meters
Volume ≈ 12.9516 cubic meters (rounded to four decimal places)
Therefore, the volume of the container is approximately 12.9516 cubic meters when rounded to the nearest hundredth.
for such more question on volume
https://brainly.com/question/6204273
#SPJ8
10+10
What is this...
Answers
Answer:
20
Step-by-step explanation:
Write an expression that represents h decreased by 5.
Answers
Answer: h - 5
Step-by-step explanation:
h decreased by 5
h - 5
I'm sorry TnT I don't really know how to explain this but I'm 100% sure my answer is correct. Hope it helped!
Answer:
see explanation
Step-by-step explanation:
h is decreased by 5
5-h
If the reliability is
r = 0.25,
the equation becomes
R(n) =
0.25n
0.75 + 0.25n
.
What percent improvement is there in the reliability when the test length is doubled?
Answers
The percentage improvement in reliability when test length is doubled is 15%
R(n) = 0.25n / (0.75 + 0.25n)
For a test length of 1substitute n = 1 into the equation :
R(n) = 0.25n / (0.75 + 0.25n)
R(1) = 0.25(1) / (0.75 + 0.25(1))
R(1) = 0.25 / 1
R(1) = 0.25
For a test length of 2when test length is doubled , n = 2
substitute n = 1 into the equation :
R(n) = 0.25n / (0.75 + 0.25n)
R(2) = 0.25(2) / (0.75 + 0.25(2))
R(2) = 0.5 / 1.25
R(2) = 0.4
Percentage improvement can be calculated thus ;
R(2)-R(1)/R(1) × 100%
(0.4-0.25)/0.25 × 100%
0.15 × 100%
=15%
Therefore, percentage improvement in reliability is 15%
Learn more on percentages : https://brainly.com/question/19994681
#SPJ9
Ali, Basti and Cian stand at three points A, B and C respectively. Suppose that the measure of angle ABC is 50 degrees , the measure of angle BAC is 60 degrees and Ali is exactly 150 ft away from Basti. Find the distance between Basti and Cian.

Answers
The distance between Basti and Cian is approximately 138.2 ft. Option D
To find the distance between Basti and Cian, we can use the Law of Sines, which relates the lengths of sides to the sines of their opposite angles in a triangle.
Let's label the points: A, B, and C. Ali is at point A, Basti is at point B, and Cian is at point C.
Given:
Angle ABC = 50 degrees (angle opposite side AC)
Angle BAC = 60 degrees (angle opposite side BC)
Ali is 150 ft away from Basti (side AB)
We want to find the distance between Basti and Cian, which is side BC.
Using the Law of Sines, we have:
BC/sin(50) = AB/sin(60)
Substituting the known values:
BC/sin(50) = 150/sin(60)
To find BC, we can rearrange the equation:
BC = (150/sin(60)) * sin(50)
Using a calculator to evaluate the expression:
BC ≈ 138.2 ft
Option D is correct.
For more such questions on distance visit:
https://brainly.com/question/30395212
#SPJ8