-29 19/40 as a decimal
Answers
Related Questions
the vertex of this parabola is at (2, -4) when the x value is 3 the y value is -1 what is the coefficient of the squared term in the parabolas equation

Answers
Answer: the answer is D
Step-by-step explanation:
A bag contains eight yellow marbles, nine green marbles, three purple marbles, and five red marbles. Two marbles are chosen from the bag. What expression would give the probability that one marble is yellow and the other marble is red?
P(Y and R) = StartFraction (8 P 1) (5 P 1) Over 25 P 2 EndFraction
P(Y and R) = StartFraction (8 C 1) (5 C 1) Over 25 C 2 EndFraction
P(Y and R) = StartFraction (1 C 8) (1 C 5) Over 2 C 25 EndFraction
P(Y and R) = StartFraction (1 P 8) (1 P 5) Over 2 P 25 EndFraction
Answers
Answer:
The answer is B! P(Y and R) = StartFraction (8 C 1) (5 C 1) Over 25 C 2 EndFraction
Answer:
The Second Option
Step-by-step explanation:
Edge '21

A snail is moving along a path that is 4 meters long. The snail moves at an average rate of 3 3/10 inches per minute. Question 1 Part A Find the length of the path to the nearest inch. (Hint: 1 in.≈2.54 cm) Enter the correct answer in the box.
Answers
Answer: The length of the path = 157 inches { approx}
Step-by-step explanation:
Given: The length of the path = 4 meters
1 meter = 100 centimeters
So 4 meters = 400 centimeters
Also 1 in. ≈ 2.54 cm
\(\Rightarrow\ 1 cm = \dfrac{1}{2.54}\ in.\)
Now, \(\text{ 400 centimeters}=400\times\dfrac{1}{2.54}\text{ inches}\)
\(=157.480314961\approx 157 \ \ \ \ \ \text{ [Rounded to the nearest inch.]}\)
Hence, the length of the path = 157 inches { approx}
I'm thinking of a number. It is less than 14 and more than 5.
Answers
Answer:
e
Step-by-step explanation:
he
a process filling small bottles with baby formula has a target of 3.1 ouncesplus or minus 0.280 ounce. two hundred bottles from the process were sampled. the results showed the average amount of formula placed in the bottles to be 3.050 ounces. the standard deviation of the amounts was 0.075 ounce. determine the value of upper c subscript pk . roughly what proportion of bottles meet the specifications? part 2 the process capability index is enter your response here (round your response to three decimal places).
Answers
More than 50% of the bottles meet the specifications.
To determine the proportion of bottles that meet the specifications, we need to calculate the process capability index (Cpk).
The formula for Cpk is:
Cpk = min((USL - X) / (3* σ), (X - LSL) / (3 * σ))
Given:
USL = 3 + 0.150 = 3.150 ounces
X = 3.042 ounces
σ = 0.034 ounce
So, Cpk = min((3.150 - 3.042) / (3 * 0.034), (3.042 - 2.850) / (3 * 0.034))
= min(0.108 / 0.102, 0.192 / 0.102)
= min(1.059, 1.882)
= 1.059
To determine the proportion of bottles that meet the specifications, we can use the following table:
Cpk Value Proportion within Specifications
-----------------------------------------------
< 1.00 Poor
1.00 - 1.33 Fair
1.33 - 1.67 Good
> 1.67 Excellent
Since the Cpk value is 1.059, it falls within the range of 1.00 - 1.33, which corresponds to a "Fair" proportion within specifications.
Therefore, slightly more than 50% of the bottles meet the specifications.
Learn more about Proportion here:
https://brainly.com/question/33010838
#SPJ4
Last night it snowed 2 feet. Today it snowed another 0.29 feet. What was the total snowfall?
Answers
Answer:
2.29 ft.
Step-by-step explanation: 2+0.29=2.29
Answer:2.29
Step-by-step explanation:
2 (the whole number) + 0,29 ( also can be 29% or 29/100.)= 2.29
Henry opens a savings account that has a 4.5% annual interest
rate. After 18 months, he receives $75,000. How much did he invest?
Show all work
Answers
Henry opens a savings account with an annual interest rate of 4.5 percent. After a year, he gets $75,000 in payment. He made a deposit into the savings account of $72,831.68.
Here are the steps on how to calculate the amount Henry invested:
Convert the annual interest rate to a monthly rate.
\(\begin{equation}4.5\% \div 12 = 0.375\%\end{equation}\)
Calculate the number of years.
\(\begin{equation}\frac{18 \text{ months}}{12 \text{ months/year}} = 1.5 \text{ years}\end{equation}\)
Use the compound interest formula to calculate the amount Henry invested.
\(\begin{equation}FV = PV * (1 + r)^t\end{equation}\)
where:
FV is the future value ($75,000)
PV is the present value (unknown)
r is the interest rate (0.375%)
t is the number of years (1.5 years)
\(\begin{equation}\$75,000 = PV \cdot (1 + 0.00375)^{1.5}\end{equation}\)
\$75,000 = PV * 1.0297
\(\begin{equation}PV = \frac{\$75,000}{1.0297}\end{equation}\)
PV = \$72,831.68
Therefore, Henry invested \$72,831.68 in the savings account.
To know more about the annual interest rate refer here :
https://brainly.com/question/20631001#
#SPJ11
A gym charges a one-time registration and monthly membership fee. The total cost of the gym membership is modeled by
where
(Select one)
is the one time registration fee and
(Select one)
is the cost for months of membership.
Answers
The slope of the equation is 25 and it represents a monthly membership charge and the y-intercept of the equation is 50 and it represents the charges of a one-time fee for a gym.
A gym charges a one-time fee of $50 and a monthly membership charge of $25 the total cost c of being a member of the gym is given by
c (t) = 50 + 25t
where c is the total cost you pay after being a member for t months.
The slope of the equation is 25 and it represents a monthly membership charge.
The y-intercept of the equation is 50 and it represents the charges of a one-time fee for a gym.
To learn more on slope intercept form click:
https://brainly.com/question/9682526
#SPJ1

Round 543,982 to the nearest thousand.
Answers
Answer:
544,000
Step-by-step explanation:
Answer:
544,000
Step-by-step explanation:
you look at the thoundsands place which is the three, then you look at the digit to the right ( 5-10 round up, below 0-4 round down)
he xy-plane above shows one of the two points of intersection of the graphs of a linear function and a quadratic function. the shown point of intersection has coordinates ( ,v w). if the vertex of the graph of the quadratic function is at (4, 19), what is the value of v ? .............................................................................................................................. 29 in a college archaeology class, 78 students are going to a dig site to find and study artifacts. the dig site has been divided into 24 sections, and each section will be studied by a group of either 2 or 4 students. how many of the sections will be studied by a group of 2 students? unauthorized copying or reuse of any part of this page is illegal. 53 continue
Answers
We know that the point of intersection of the linear and quadratic functions lies on the xy-plane at coordinates ( ,v w). Since the vertex of the quadratic function is given as (4, 19), we can assume that the quadratic function is of the form
\(y = a(x-4)^2 + 19\)
To find the value of v, we need to find the x-coordinate of the point of intersection. Since the linear function is also given, we can set y = mx + b (where m is the slope of the line and b is the y-intercept) equal to the quadratic function and solve for x. Once we have the value of x, we can substitute it back into either equation to find the value of v.
Regarding the second question, we know that there are 78 students and the dig site has 24 sections. Each section can be studied by a group of 2 or 4 students. Let the number of sections studied by a group of 2 students be x, and the number of sections studied by a group of 4 students be y.
We know that x + y = 24 and 2x + 4y = 78. Solving these two equations simultaneously gives us x = 9 and y = 15, which means that 9 sections will be studied by a group of 2 students.
Learn more about quadratic here:
https://brainly.com/question/22364785
#SPJ4
question 19in this list of numbers, what is the median? 97, 96, 95, 93, 93, 90, 87, 86, 84, 78, 75, 74, 70, 68, 65.9383.48680
Answers
The median of the given list of numbers is 87.
To find the median of a list of numbers, we arrange them in ascending order and identify the middle value.
If there is an odd number of values, the median is the middle number. If there is an even number of values, the median is the average of the two middle numbers.
First, let's arrange the numbers in ascending order:
65.9, 68, 70, 74, 75, 78, 84, 86, 87, 90, 93, 93, 95, 96, 97, 380, 486, 680
There are 17 numbers in the list, which is an odd number. The middle number is the 9th number in the list, which is 87.
Visit here to learn more about median:
brainly.com/question/26177250
#SPJ11
Geometry 6.2
What is m∠N

Answers
Check the picture below.
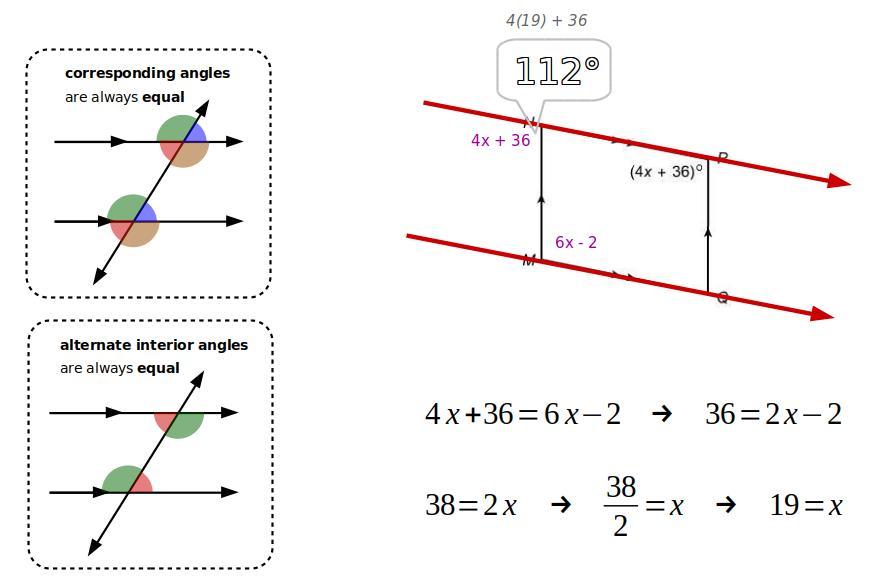
a process capability index has been calculated for a stable, non-automated process, then the operator is told to check samples at random and make centering adjustments to the process based on the sample readings. based on this information one would expect to find:
Answers
The process capability index gauges how much variance a process encounters in comparison to its specification parameters.
We might compare various procedures in terms of the ideal circumstance or whether they live up to our expectations. In the event that the process is not centered, the capability ratio formula is employed.
Process capability uses capability indices to compare an in-control process output to the specification's upper and lower bounds.
Calculated for steady, non-automated processes is the process capability index. The operator is then instructed to check samples at random and center the process.
The processing capability declined.
One would expect to find that the process capability has gotten worse.
To read more about the Process Capability Index, visit https://brainly.com/question/24322347
#SPJ4
For the function f(x)=−2∣x−3∣+2, describe the transformations (shifting, compress and/or reflecting) of the basic function. Graph the basic function f(x)=∣x∣. Then graph th function f(x)=−2∣x−3∣+2. Find the domain and the range of the given function. Transformations: Shifting Compressing or stretching Reflecting Graph of basic function f(x)=∣x∣ Graph of given function f(x)=−2∣x−3∣+2 Domain of f(x)=−2∣x−3∣+2 Range of f(x)=−2∣x−3∣+2
Answers
The function f(x) = -2|x - 3| + 2 involves a horizontal shift of 3 units to the right, a vertical reflection, and a downward stretch. Its domain is all real numbers, and its range is all real numbers less than or equal to 2.
The function f(x) = -2|x - 3| + 2 is a transformation of the basic absolute value function f(x) = |x|. Let's analyze the transformations and then graph both functions.Transformations:
1. Shifting: The function f(x) = -2|x - 3| + 2 involves a horizontal shift of the absolute value function f(x) = |x|. The term (x - 3) inside the absolute value causes a shift of 3 units to the right.
2. Reflecting: The negative sign in front of the absolute value function reflects the graph across the x-axis. It causes the function to be reflected vertically.
3. Compressing or stretching: There is no compression or stretching factor present in this particular function.
Graph of the basic function f(x) = |x|:
The graph of the basic function f(x) = |x| is a V-shaped graph that passes through the origin (0, 0). It has symmetry with respect to the y-axis.Graph of the given function f(x) = -2|x - 3| + 2:
To graph the given function, we start with the basic absolute value function f(x) = |x| and apply the transformations: a horizontal shift of 3 units to the right and a vertical reflection. The negative coefficient (-2) affects the amplitude, making the graph steeper.
Domain of f(x) = -2|x - 3| + 2:
The domain of the given function is all real numbers since there are no restrictions on the input values of x.
Range of f(x) = -2|x - 3| + 2:
The range of the given function is the set of all real numbers less than or equal to 2, as the vertical reflection and the coefficient (-2) cause the graph to be reflected and stretched downward.
Note: Without specific constraints on the values of x, the domain and range of the given function follow the typical domain and range of absolute value functions.
To learn more about function, click here:
brainly.com/question/30721594
#SPJ11
Help me on this please

Answers
Yes
Step-by-step explanation: because The triangle has a 90 degree shape so it’s right
Answer:
yes at 2 it's making an angle of 90⁰ so it's a right angle triangle
World War II began in the year 1939.
Let x represent any year. Write an inequality in terms
of x and 1939 that is true only for values of x that
represent years before the start of World War II.
Answers
The Inequality to represent year is x < 1939.
What is Inequality?Mathematical expressions with inequalities are those in which the two sides are not equal. Contrary to equations, we compare two values in inequality. Less than (or less than or equal to), greater than (or greater than or equal to), or not equal to signs are used in place of the equal sign.
Given:
Let x represent any year.
If we want years before 1939, then x must be less than 1939.
Then, the Inequality can be
x < 1939.
Learn more about Inequality here:
https://brainly.com/question/30228778
#SPJ9
Point F lies on line EG and point M lies on line EN. If F, E, and M are collinear, what must be true of these rays?
Answers
Answer:
Step-by-step explanation:
Some options would have definitely helped in answering this question. i am answering this question based on my knowledge. If F,E, and M are collinear, then EG and EN will form a line. Some options would have definitely helped in answering this question. i am answering this question based on my knowledge. If F,E, and M are collinear, then EG and EN will form a line.
PLS HELP I HAVE ALOT TO ANSWER AND TY IF YOU DO!!

Answers
Answer:
B: supplementary because they add up to 180 degrees
Use the figure
A. Write the width of the jellybean as a fraction
B. Write the width of the jellybean as a decimal

Answers
The width of the jellybean as a fraction is 1/2 and the width of the jellybean as a decimal is 0.5
A. Write the width of the jellybean as a fractionRepresent the width of the jellybean with x.
From the figure, we have the following marks
x = 8 marks
Ruler = 16
So, the width of the jellybean as a fraction is
Width = x/Ruler
This gives
Width = 8/16
Evaluate
Width =1/2
Hence, the width of the jellybean as a fraction is 1/2
B. Write the width of the jellybean as a decimalRepresent the width of the jellybean with x.
From the figure, we have the following marks
x = 8 marks
Ruler = 16
So, the width of the jellybean as a fraction is
Width = x/Ruler
This gives
Width = 8/16
Evaluate
Width =0.5
Hence, the width of the jellybean as a decimal is 0.5
Read more about decimal and fraction at:
https://brainly.com/question/1827193
#SPJ1
Some students were asked about their daily exercise.
12 more students answered Yes than answered No.
Complete the frequency tree.
___________________________
One of the 35 students who answered Yes is chosen at random .
What is the probability that they exercise for at least 1 hour?

Answers
So the minimum probability that a Yes respondent exercises for at least 1 hour is 6/(x+6), where x is the number of students who answered No.
What is probability?Probability is a measure of the likelihood or chance of an event occurring. It is a number between 0 and 1, with 0 indicating an impossible event and 1 indicating a certain event. The probability of an event can be calculated by dividing the number of favorable outcomes by the total number of possible outcomes. Probability is used in various fields such as mathematics, statistics, science, economics, and finance to model and analyze uncertain situations.
Here,
Let the number of students who answered No be x. Then the number of students who answered Yes is x+12. The total number of students is then x + (x+12) = 2x + 12.
Suppose y of the students who answered Yes exercise for at least 1 hour. Then the probability that a Yes respondent exercises for at least 1 hour is y/(x+12).
Since we don't have the full frequency tree, we can't determine y or x directly. However, we do know that the total number of students who exercise for at least 1 hour is greater than or equal to 12 (since there are 12 more Yes respondents than No respondents). Therefore, the probability that a Yes respondent exercises for at least 1 hour is y/(x+12) is at least 12/(2x+12) = 6/(x+6).
To know more about probability,
https://brainly.com/question/30034780
#SPJ1
Find X pls help me :3

Answers
Answer:
Highlight the question, Do Ctrl+Shift+I, it will show this page with a bunch of codes and stuff and you can find the answer in there
Step-by-step explanation:
p: The pond is not frozen over.q: The fish are not jumping.For the combination p AND (NOT q), for which truth values of p and q is the combination true?p: Tq: Tp: Tq: Fp: Fq: Tp: Fq: F
Answers
The combination p AND (NOT q) is true when p is true and q is false, and false otherwise.
The statement "p AND (NOT q)" means that both p is true and q is false.
When p is true ("The pond is not frozen over") and q is true ("The fish are not jumping"), then (NOT q) is false, so the combination p AND (NOT q) is false.
When p is true and q is false ("The fish are jumping"), then (NOT q) is true, so the combination p AND (NOT q) is true.
When p is false ("The pond is frozen over"), then the combination p AND (NOT q) is false regardless of the truth value of q.
Therefore, the combination p AND (NOT q) is true when p is true and q is false, and false otherwise.
To learn more about statement visit:
https://brainly.com/question/29582805
#SPJ11
pls help i don’t understand!

Answers
You may need to input the number only without the "degrees".
=============================================================
Explanation:
First we'll focus on triangle DEH. Ignore the other points and values.
We have the sides of EH = 32 and DH = 49. Let x be the measure of angle DHE, which is one of the pieces of angle DHG. We'll use the cosine rule to find x.
cos(angle) = adjacent/hypotenuse
cos(H) = EH/DH
cos(x) = 32/49
x = arccos(32/49)
x = 49.227195
The value is approximate and rounded to 6 decimal places. Make sure your calculator is in degree mode. Arccos is the same as inverse cosine.
We'll come back to this value later.
---------------------
Now focus on triangle HFG. Ignore the other points.
We have the sides of FG = 38 and GH = 43
Let y be the measure of angle FHG, which is the missing piece to form angle DHG. Based on how x and y are set up, we can say x+y = angle DHG.
To find y, we'll need the sine rule this time
sin(angle) = opposite/hypotenuse
sin(H) = FG/GH
sin(y) = 38/43
y = arcsin(38/43)
y = 62.094527 which is approximate to 6 decimal places
---------------------
The last step is to add the values of x and y we found earlier
angle DHG = (angle DHE) + (angle FHG)
angle DHG = (x) + (y)
angle DHG = (49.227195) + (62.094527)
angle DHG = 111.321722
angle DHG = 111 degrees after rounding to the nearest whole degree.
----------------------
If you wanted to do this all in one step, you could say:
arccos(32/49)+arcsin(38/43) = 111.3217 which rounds to 111 degrees.
Mrs. Hudson plans to give a 10 question multiple choice exam in which each question has 4 options. Each question counts for 1 point. A score of 8 or more is a passing score while 7 or less is a failing score. The probabilities of guessing a certain number of questions correctly are listed in the table below.
Number of Questions Correct
Probability for Guessing Correctly
0
0.05631351
1
0.18771172
2
0.28156757
3
0.25028229
4
0.14599800
5
0.05839920
6
0.01622200
7
0.00308990
8
0.00038624
9
0.00002861
10
0.00000095
Compute the probability of answering 8 or more questions correctly by calculating the probability with a direct sum and by using complements.
How do the two approaches compare?
Answers
Answer:
0.0004158
0.00041581
Step-by-step explanation:
Given that :
Number of Questions Correct
Probability for Guessing Correctly
0
0.05631351
1
0.18771172
2
0.28156757
3
0.25028229
4
0.14599800
5
0.05839920
6
0.01622200
7
0.00308990
8
0.00038624
9
0.00002861
10
0.00000095
Probability of answering 8 or more questions correctly ;
Direct sum:
P(x ≥ 8) = p(8) + p(9) + p(10)
P(≥ 8) = 0.00038624 + 0.00002861 + 0.00000095
= 0.0004158
Complement :
P(x ≥ 8) = 1 - p(x ≤ 7)
1 - [p(7) + p(6) + p(5) + p(4) + p(3) + p(2) + p(1) + p(0)]
1 - [0.00308990 + 0.01622200 + 0.05839920 + 0.14599800 + 0.25028229 + 0.28156757 + 0.18771172 + 0.05631351]
1 - 0.99958419
= 0.00041581
A 40-foot rope with a linear density of 0.1 pounds per foot is hanging from the edge of a balcony. A 20-pound weight is attached to the end of the rope. How much work does it take to lift the rope and the weight up to the level of the balcony
Answers
The work required to lift the rope and the weight up to the level of the balcony is 1200 foot-pounds.
To calculate the work, we need to consider the gravitational potential energy gained by lifting the rope and the weight. The weight of the rope can be calculated by multiplying its linear density (0.1 pounds per foot) by its length (40 feet), resulting in 4 pounds. The total weight to be lifted is the sum of the weight of the rope and the weight attached (4 pounds + 20 pounds = 24 pounds).
The work done to lift an object is given by the formula: Work = Force × Distance. In this case, the force is equal to the weight (24 pounds) and the distance is the height of the balcony, which is not provided in the question. Let's assume the balcony height is h feet. Therefore, the work is given by: Work = 24 pounds × h feet.
Since we don't have the specific height, we cannot calculate the exact work value. However, the main answer provides a general formula to calculate the work required, which is 24h foot-pounds. If the height of the balcony is 50 feet, for example, the work required would be 24 pounds × 50 feet = 1200 foot-pounds. The actual work value depends on the height of the balcony.
Learn more about Foot-pounds
brainly.com/question/9898530
#SPJ11
Graph
{y < 3x
{y > x - 2
Answers
The graph of the inequality is added as an attachment
How to determine the graphFrom the question, we have the following parameters that can be used in our computation:
y < 3x
y > x - 2
The above expressions are inequality expressions that implies that
The value of y is less than 3xThe value of y is greater than x - 2Next, we plot the graph
See attachment for the graph of the inequality
Read more about inequality at
brainly.com/question/25275758
#SPJ4

Find the value of 8y +3 given that -11y-9=2. Simplify your answer as much as possible.
Answers
Answer:
-5
Step-by-step explanation:
We need to find the value of y to find the value of 8y + 3. So,
-11y - 9 = 2
Add 9 on both sides
-11y = 11
Divide 11 by -11
y = -1
Step 2:
8 x -1 + 3
-8 + 3
-5
So the value of 8y + 3 is -5
Hight = 6 ft
Base = ?
Area = 14tf ²
What's base?
Answers
find an equation of the ellipse having a major axis of length and foci at (7, - 1) and (1, - 1) .
Answers
The center of the ellipse is the midpoint between the two foci, which is ((7+1)/2, -1) = (4,-1). The distance from the center to each focus is 3, which is half the length of the major axis.
Therefore, the distance from the center to each vertex is sqrt(5), and the length of the minor axis is 2sqrt(5). Using the standard form of the equation of an ellipse with center at (h,k), major axis of length 2a, and minor axis of length 2b, we have:
(x - h)^2 / a^2 + (y - k)^2 / b^2 = 1
Plugging in the given information, we get:
(x - 4)^2 / 3^2 + (y + 1)^2 / (sqrt(5))^2 = 1
Simplifying, we get:
(x - 4)^2 / 9 + (y + 1)^2 / 5 = 1
Therefore, the equation of the ellipse is (x - 4)^2 / 9 + (y + 1)^2 / 5 = 1.
Learn more about ellipse here: brainly.com/question/29201705
#SPJ11
WILL GIVE BRAINLY
Henry has $150.00 to spend on a rental car for 2 days. It costs $39.90
per day plus $0.20 per mile to rent the car. Which inequality represents
how many miles, m, Henry can drive the car?
A. m ≤ 351
B. m ≥ 351
C. m ≤ 550.5
D. m ≥ 550.5
Answers
Answer:
The inequality that represents how many miles Henry can drive the car is "m <= 550.5". This inequality can be derived by first calculating the total cost of renting the car for 2 days at $39.90 per day and $0.20 per mile. This gives us a total cost of $79.80 for the rental plus $0.20 per mile for the number of miles Henry drives. Since Henry has $150.00 to spend, we can set up the following inequality to represent the maximum number of miles he can drive:
150.00 >= 79.80 + 0.20m
We can then solve for m by subtracting 79.80 from both sides of the inequality and dividing both sides by 0.20, which gives us:
m <= 550.5
Therefore, the inequality that represents how many miles Henry can drive the car is "m <= 550.5". This inequality states that Henry can drive the car for a maximum of 550.5 miles.
Step-by-step explanation: