1.
What are the solutions to the equation 0 = x2-x-6?
Answers
Related Questions
A line that includes the point (10, 7) has a slope of 10 . What is its equation in slope-intercept form?
Answers
y = mx + b
10 = 3*1 + b
b = 7
y = 3x + 7
Answer:
y=3x+7
Step-by-step explanation:
subtract 7 from 10 to get answer
example 3 video example find x 2 − 3x2 dx . solution let u = 2 − 3x2. then du = dx, and x dx = du and x 2 − 3x2 dx = · 1 u du = · u−1/2 du = 2 u c = c (in terms of x).
Answers
To solve this, we can make a substitution. Let u = 2 − 3x^2. Then, we differentiate both sides with respect to x to find du/dx = -6x.
Solving for dx, we have dx = du / (-6x). Substituting these expressions back into the integral, we get:
∫(x^2 − 3x^2) dx = ∫(x^2 − 3x^2) (du / (-6x))
Next, we simplify the integrand:
= ∫((-2x^2 + 3x^2) du / (6x))
= ∫(x^2 du / 6x)
= (1/6) ∫(x du)
= (1/6) ∫u du
Integrating u with respect to u, we get:
= (1/6) * (u^2 / 2) + C
= (1/12) * u^2 + C
Finally, substituting back u = 2 − 3x^2, we have:
= (1/12) * (2 − 3x^2)^2 + C
= (1/12) * (4 − 12x^2 + 9x^4) + C
Simplifying further, we get the final solution:
= (1/12) * (9x^4 − 12x^2 + 4) + C
This is the integral of x^2 − 3x^2 dx in terms of x.
Learn more about integrand here: brainly.com/question/31963820
#SPJ11
Use the graph of the polynomial function f(x)= -x^3 + 5x^2 - 2x - 8 to complete the sentences:
f is _____ on the intervals (-∞, 1/3) and (3, ∞).
f is _____ on the intervals (-1, 2) and (4, ∞).
f is _____ on the intervals (1/3, 3)
f is _____ on the intervals (-∞, -1) and (2, 4).

Answers
a) f is positive on the intervals (-∞, 1/3) and (3, ∞).
b) f is negative on the intervals (-1, 2) and (4, ∞).
c) f is decreasing on the interval (1/3, 3) for a given polynomial function.
d) f is increasing on the intervals (-∞, -1) and (2, 4).
What are polynomial functions?Polynomial functions are functions that are defined by polynomial expressions. A polynomial expression is a finite sum of terms that are each monomial expression, which means they consist of a constant coefficient multiplied by a variable raised to a non-negative integer power.
The general form of a polynomial function is:
f(x) = \(a_n\) \(x^{n\) + \(a_{n-1}\)\(x^{{n-1}}\) + ... + \(a_1 x\) + a_0
where n is a non-negative integer, \(a_n\), \(a_{n-1}\), ..., \(a_1,\) \(a_0\) are constants (called the coefficients), and x is the variable.
According to the given informationUsing the graph of the polynomial function f(x) = -\(x^{3}\) + 5\(x^{2}\) - 2x - 8, we can complete the sentences as follows:
a) f is positive on the intervals (-∞, 1/3) and (3, ∞). This is because the graph of the function is above the x-axis on these intervals.
b) f is negative on the intervals (-1, 2) and (4, ∞). This is because the graph of the function is below the x-axis on these intervals.
c) f is decreasing on the interval (1/3, 3). This is because the graph of the function is sloping downward from left to right on this interval.
d) f is increasing on the intervals (-∞, -1) and (2, 4). This is because the graph of the function is sloping upward from left to right at these intervals.
To know more about polynomial functions visit:
brainly.com/question/12976257
#SPJ1
Geometry the area of a trapezoid is given by the formula a = 1 2 h ( a + b ) , where h is the height and a and b are the measures of the two bases. what is the height of a trapezoid with an area of 24 square inches if the two bases measure 4 inches and 6 inches?
Answers
The formula for the area of a trapezoid is given as, a = 1/2 h (a + b) Where, a and b are the measures of two bases of the trapezoid and h is the height of the trapezoid. The area of the trapezoid is given as 24 square inches and the two bases of the trapezoid measure 4 inches and 6 inches.
We need to find the height of the trapezoid. Using the given formula, we can find the height of the trapezoid as below: 24 = 1/2 h (4 + 6)
Simplifying the above expression, we get: 24 = 5h
Hence, the height of the trapezoid is 24/5 or 4.8 inches.
Trapezoid is a quadrilateral with only one pair of parallel sides. The bases of the trapezoid are those parallel sides and the height of the trapezoid is the perpendicular distance between the two bases. In this question, the area of the trapezoid is given as 24 square inches and the two bases of the trapezoid measure 4 inches and 6 inches. We need to find the height of the trapezoid.
Simplifying the above expression, we get:24 = 5h
Hence, the height of the trapezoid is 24/5 or 4.8 inches.
To know more about inches visit:
https://brainly.com/question/32203223
#SPJ11
I'm confused about what the expression is.

Answers
Answer:
4(x+y)
Step-by-step explanation:
x+y is one side length and there are 4 side lengths.
simplify: (2x-3)(5x+1)
Answers
Answer:
\(\huge\boxed{\sf 10x^2-13x-3}\)
Step-by-step explanation:
\(=(2x-3)(5x+1)\\\\=2x(5x+1)-3(5x+1)\\\\Distribute\\\\= 10x^2+2x-15x-3\\\\= 10x^2-13x-3\\\\\rule[225]{225}{2}\)
10x² - 13x - 3
Step-by-step explanation:
(2x - 3) (5x + 1)
Apply distributive property ,
= 2x(5x + 1) - 3(5x + 1)
= 10x² + 2x - 15x - 3
= 10x² - 13x - 3
__________
Hope it helps ⚜
What is the volume of a ball if its diameter is 6 inches? Leave your answer in terms of π.
A) V = 12 π cubic inches
B) V = 36 π cubic inches
C) V = 288 π cubic inches
D) V = 27.75 π cubic inches
Answers
Answer:
B
Step-by-step explanation:
I am assuming that this ball is a perfect sphere.
The volume of a sphere is \(\frac{4}{3} *\pi *r^3\)
We have the diameter, and in order to find the radius, we just have to divide by 2. 6/2=3. Now, we have to plug in the 3 to the equation.
\(\frac{4}{3} *\pi *3^3\)
3 cubed is 27, so now we have \(\frac{4}{3} *\pi *27\)
27*4/3*pi=36pi
Find the value of c
-x^2 -22x + c
Answers
Answer:
−(x+11− square root of 121+c )(x+11+ square root of 121+c)
Step-by-step explanation: hoped I helped
Find the derrivative of f(x,y,z) = xy + xz + yz at point p(1,
-2, 2) in the direction of 10i + 11j - 2k.
Answers
To find the derivative of the function f(x, y, z) = xy + xz + yz at point P(1, -2, 2) in the direction of 10i + 11j - 2k, we use the directional derivative formula. The derivative of f(x, y, z) in the given direction is 39.
The directional derivative of a function f(x, y, z) in the direction of a unit vector v = ai + bj + ck is given by the dot product of the gradient of f(x, y, z) and the unit vector v.
First, we calculate the gradient of f(x, y, z):
∇f(x, y, z) = (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k = yi + xi + xj + yk + zk + yj = (y + z)i + (x + z)j + (x + y)k.
Next, we find the unit vector in the given direction:
v = 10i + 11j - 2k.
Then, we take the dot product of the gradient and the unit vector:
∇f(x, y, z) · v = ((y + z)i + (x + z)j + (x + y)k) · (10i + 11j - 2k) = (y + z)(10) + (x + z)(11) + (x + y)(-2) = 10y + 10z + 11x + 11z - 2x - 2y.
Finally, we substitute the values of x, y, and z from point P(1, -2, 2):
∇f(1, -2, 2) · v = 10(-2) + 10(2) + 11(1) + 11(2) - 2(1) - 2(-2) = 39.
Therefore, the derivative of f(x, y, z) at point P(1, -2, 2) in the direction of 10i + 11j - 2k is 39.
Learn more about vector here: brainly.com/question/29740341
#SPJ11
Answer these please!!!

Answers
The graph of 3x-2y≤6 is the third graph, for 3x-2y<6 is the first graph, for 3x-2y>6 is the fourth graph and for 3x-2y≥6 is the second graph. The solution has been obtained using concept of linear inequality.
What is linear inequality?
A linear inequality is one that would produce a linear equation if the equals relation were used instead of the inequality. When multiplying or dividing both sides by a negative number in order to solve the inequality, the direction of the inequality is reversed. The entire set of solutions to an inequality is known as the solution set.
We are given for graphs, of which two graphs are dotted and two are simple straight line graphs.
The dotted graphs are drawn for the inequalities having < or >
Whereas the simple straight line graphs are drawn for the inequalities having ≤ or ≥.
Now, to notice the shaded pattern, we will see whether the equations are true for (0,0) or not
1. 3x-2y≤6
⇒ 0≤6
So, the equation is true for the point.
Hence, the third graph represents this equation.
2. 3x-2y<6
⇒ 0<6
So, the equation is true for the point.
Hence, the first graph represents this equation.
3. 3x-2y>6
⇒ 0>6
So, the equation is false for the point.
Hence, the fourth graph represents this equation.
4. 3x-2y≥6
⇒ 0≥6
So, the equation is false for the point.
Hence, the second graph represents this equation.
Hence, the graphs are matched with the inequalities.
Learn more about linear inequality from the given link
https://brainly.com/question/30340033
#SPJ1
Since, there are multiple questions so, the question answered above is attached below.

Evaluate. Remember Order of
Operations! (PEMDAS)
-56 ÷ 8 × (-7 + 4) = [?]
Enter
Answers
Answer:
21Step-by-step explanation:
-56÷8×(-7+4)=-56÷8×-3=21Does Anybody know who this is!??!

Answers
That would be Tobey Maguire an American Actor best known from Spider Man. Recently made a comeback in no way home.
Answer:
Toby Miguire that is!
Step-by-step explanation:
Simplify for a = 3, b = -4 and c = -1.
2a(b−c)
Answers
Answer:
your answer would be -18
Find the period of the function f(x) = cos(2.22x+0.19). Provide four decimal places. Answer:______ Find the period of the function f(x) = sin(1.05x). Provide four decimal places. Answer:______
Answers
The period of the function f(x) = cos(2.22x+0.19) is 2.8323 and the period of the function f(x) = sin(1.05x) is 5.9834
The period of a trigonometric function, we use the formula:
Period = 2π/|B|
where B is the coefficient of x in the function.
For the first function, f(x) = cos(2.22x+0.19), the coefficient of x is 2.22. Therefore, the period is:
Period = 2π/|2.22| ≈ 2.8323
For the second function, f(x) = sin(1.05x), the coefficient of x is 1.05. Therefore, the period is:
Period = 2π/|1.05| ≈ 5.9834
So, the period of the first function is 2.83 and the period of the second function is 5.98. Both answers are rounded to four decimal places.
To know more about period of a trigonometric function refer here:
https://brainly.com/question/28483432
#SPJ11
HELLPPP
Solve the system by substitution.
-9x-10y=12
−3x+3=y
Answers
Solve the system by substitution.
-9x-10y=12
−3x+3=y
X=2
Y= -3
Answer:
\(x=2\\y=-3\)
Step-by-step explanation:
We have:
\(-9x-10y=12\\-3x+3=y\)
Since we already have a variable value (\(y\)) in the second equation, it would be easiest to substitute the value for \(y\) in the first equation:
\(-9x-10(-3x+3)=12\)
Distribute \(-10\) into \((-3x+3)\):
\(-9x+30x-30=12\)
Combine like terms:
\(21x-30=12\)
Add \(30\) to both sides of the equation:
\(21x=42\)
Divide by the coefficient of \(x\), which is \(21\):
\(x=2\)
_
Now that we have our \(x\) value, we can substitute that in to the second equation to find our \(y\) value:
\(-3(2)+3=y\)
Multiply:
\(-6+3=y\)
Combine like terms:
\(-3=y\)
Need help ASAP pls help

Answers
Answer: The correct answers are B, D, and F.
Step-by-step explanation: B is correct because 8 x 5 is 40, and 40-5 is less than or equal to 36. C is correct because if you plug in 41/8, the answer is 36. Anything higher than 41/8 is greater than 36. F is correct because 5 is a solution and 5 is less than 41/8. Therefore, the correct answers are B, D, and F.
What is (5 x 1,000,000) (6 x 100,000) (4 x 10,000) (8 x 1,000) (3 x 100) (2 x 10) (4 x 0.1) (9 x 0.001) in standard form?
Answers
The standard form of the given numbers is 207360 × 10¹⁷.
What is a number system?The number system is a way to represent or express numbers.
A decimal number is a very common number that we use frequently.
Since the decimal number system employs ten digits from 0 to 9, it has a base of 10.
Any of the multiple sets of symbols and the guidelines for utilizing them to represent numbers are included in the Number System.
Given the numbers is (5 x 1,000,000) (6 x 100,000) (4 x 10,000) (8 x 1,000) (3 x 100) (2 x 10) (4 x 0.1) (9 x 0.001)
Now standard form means we need to write the exponents form.
So,
5 x 6 x 4 x 8 x 3 x 2 x 4 x 9 = 207360
And
1,000,000 x 100000 x 10000 x 1000 x 100 x 10 x 0.1 x 0.001 = 10¹⁷
So, combine 207360 x 10¹⁷
Hence "The standard form of the given numbers is 207360 × 10¹⁷".
For more about the number system,
https://brainly.com/question/22046046
#SPJ1
AC is a diameter of OE, the area of the
circle is 289 units2, and AB = 16 units.
Find BC and mBC.
B
A
C
E. plssss hurry !!

Answers
The measure of arc BC is 720 times the measure of angle BAC.
Given that AC is the diameter of the circle and AB is a chord with a length of 16 units, we need to find BC (the length of the other chord) and mBC (the measure of angle BAC).
To find BC, we can use the property of chords in a circle. If two chords intersect within a circle, the products of their segments are equal. In this case, since AB = BC = 16 units, the product of their segments will be:
AB * BC = AC * CE
16 * BC = 2 * r * CE (AC is the diameter, so its length is twice the radius)
Since the area of the circle is given as 289 square units, we can find the radius (r) using the formula for the area of a circle:
Area = π * r^2
289 = π * r^2
r^2 = 289 / π
r = √(289 / π)
Now, we can substitute the known values into the equation for the product of the segments:
16 * BC = 2 * √(289 / π) * CEBC = (√(289 / π) * CE) / 8
To find mBC, we can use the properties of angles in a circle. The angle subtended by an arc at the center of a circle is double the angle subtended by the same arc at any point on the circumference. Since AC is a diameter, angle BAC is a right angle. Therefore, mBC will be half the measure of the arc BC.
mBC = 0.5 * m(arc BC)
To find the measure of the arc BC, we need to find its length. The length of an arc is determined by the ratio of the arc angle to the total angle of the circle (360 degrees). Since mBC is half the arc angle, we can write:
arc BC = (mBC / 0.5) * 360
arc BC = 720 * mBC
Therefore, the length of the arc BC equals 720 times the length of the angle BAC.
for such more question on measure of arc
https://brainly.com/question/25716982
#SPJ8
Can someone help please

Answers
9514 1404 393
Answer:
16.4
Step-by-step explanation:
The law of cosines is useful here. It tells you ...
b^2 = a^2 + c^2 -2ac·cos(B)
b^2 = 22^2 +10^2 -2·22·10·cos(44°)
b^2 ≈ 267.49
b ≈ √267.49 ≈ 16.35514
b ≈ 16.4

(((4\sqrt(2) - 2 \sqrt(6)) - (\sqrt(2)- \sqrt(6) )))/(\sqrt(3)-1)
Answers
Answer:
thx for points
Consider the equation Ax+By=−36. If the x-intercept is (−3,0) and the y-intercept is (0,9), what are the values of A and B?
Answers
Answer:
A= 12
B = -4
Step-by-step explanation:
( -3,0) & (0,9) should satisfy the equation Ax + By = -36
when ( -3,0)
-3A+ 0 = -36
A = 12
when (0,9)
0 + 9B = -36
B = -4
The value of A and B is 12 and -4.
Given that,
The equation is Ax + By = -36.And, the x-intercept is (-3,0) and the y-intercept is (0,9).Based on the above information, the calculation is as follows:
Ax + By = -36
When (-3,0)
So,
-3A+ 0 = -36
A = 12
Now
when (0,9)
So,
0 + 9B = -36
B = -4
Therefore we can conclude that the value of A and B is 12 and -4.
Learn more: brainly.com/question/3334417
a circle with diameter $2$ is translated $5$ units. what is the perimeter of the region swept out by the circle?
Answers
The perimeter of the region swept out by the circle during translation is 2π units.
When a circle is translated, its shape remains the same, but its position in space changes. The perimeter of the region swept out by the circle during translation will be the same as the perimeter of the circle itself.
Given:
Diameter of the circle = 2 units
Translation distance = 5 units
Calculate the radius of the circle.
Radius (r) = Diameter / 2
r = 2 / 2
r = 1 unit
Calculate the perimeter of the circle.
Perimeter of a circle (P) = 2 x π x r
P = 2 x π x 1
P = 2π units
Therefore, the perimeter of the region swept out by the circle during translation is 2π units.
To know more about perimeter follow
https://brainly.com/question/32228528
#SPJ12
please help me please

Answers
Answer:
1. 6 2. 8 3. 4 4.40 5 . 4 Step-by-step explanation:
What is the slope?
Simplify your answer and write it as a proper fraction, improper fraction, or integer.

Answers
7, 3, -1, -5, … What is the 7th value in the sequence?
Answers
Answer:
- 17Step-by-step explanation:
7
3 = 7 - 4
-1 = 3 - 4
-5 = -1 - 4
so the 5th: -5 - 4 = -9
the 6th: -9 - 4 = -13
and the 7th: -13 - 4 = -17
Complete the statements describing the effect of the outlier on the measures of variability. the outlier of the data set is . the range of the data set including the outlier as the minimum is more than the one excluding the outlier as the minimum. the outlier had the most effect on the .
Answers
the outlier may also affect the median, as the median value corresponds to the midpoint of the data set.
An outlier is an observation that differs significantly from other observations in a data set. The range of a data set measures the difference between the highest and lowest values in the set. When an outlier is included as the minimum value of the data set, the range of the data set increases due to the large difference between the outlier and the other data points. Therefore, the outlier had the most effect on the range of the data set.
The outlier had an impact on other measures of variability as well. For example, the inclusion of the outlier may increase the variance of the data set. This is because the outlier increases the difference between all the observations and the mean, thus increasing the variability of the data set. The outlier also affects the interquartile range, as it increases the difference between the upper and lower quartiles. In addition, the outlier may also affect the median, as the median value corresponds to the midpoint of the data set.
Learn more about median here
https://brainly.com/question/15323584
#SPJ4
For problems 1, 2, and 3, use the function g(x) = sin(6x) .
1. Find the amplitude of the function. State the range of the function.
2. Find the period of the function. Find the key points of the function [intercept(s), maximum(s), and minimum(s)] for 1 period. Show all work.
3. Sketch the graph of g (one period), alongside the graph of f(x) = sinx on the interval [0,2/pi]. Label the axes.
For problems 4, 5, and 6, use the function g(x)=cos((x)/(4)).
4. Find the amplitude of the function. State the range of the function.
5. Find the period of the function. Find the key points of the function [intercept(s), maximum(s), and minimum(s)] for 1 period. Show all work.
6. Sketch the graph of g, alongside the graph of f(x) = cosx on the interval [0,2/pi] . Label the axes.
Answers
Step-by-step explanation:
1. Amplitude = 1. g(x) = 1 sin(6x). The coefficient 1 is the amplitude. The range of the function is \(-1 \le g(x) \le 1\) or, in interval notation, [-1, 1]
2. The period is \(\frac{2\pi}{6}=\frac{\pi}{3}\).
x-intercepts (at the beginning, middle, and end of the period) \(0,\,\frac{\pi}{6},\,\frac{\pi}{3}\)
Maximum (1/4 of way through period) \(\left(\frac{\pi}{12},\,1 \right)\)
Minimum (3/4 of way through period) \(\left( \frac{\pi}{4}, \, -1 \right)\)

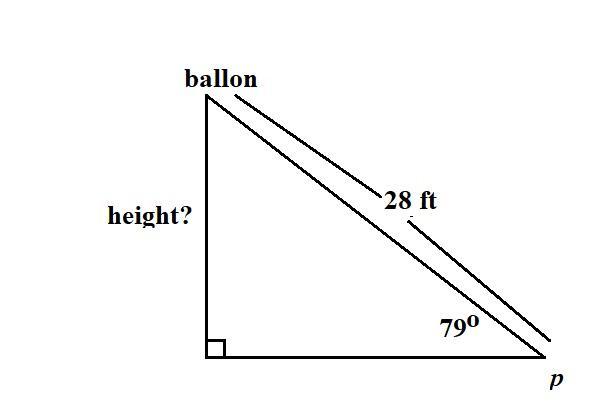
A balloon rises vertically from point p on level ground. From point a, on level ground 28ft from point p, the angle of elevation to the balloon is 79\deg . How high is the balloon?
Answers
Answer: Balloon is 27.5 ft high.
Step-by-step explanation:
As per the give , we made a diagram (in attachment).
To find the vertical distance from the growth we consider entire triangle as right triangle , where height is making right angle with ground.
in right triangle,
\(\sin \theta=\dfrac{Hypoteuse}{height}\\\\\Rightarrow\ \sin 79^{\circ}=\dfrac{28}{height}\\\\\Rightarrow\ 0.98162718344=\dfrac{28}{height}\\\\\Rightarrow\ height = 0.98162718344\times28\\\\\Rightarrow\ height = 0.98162718344\times28\approx27.5\)
hence, balloon is 27.5 ft high.
Can someone pls help with this question.

Answers
Answer:
6 litres
Step-by-step explanation:
.80 * 6 = 4.80
Mark can buy 6 litres of milk for 80p per.
leaving 20p left, of his £5
hope this helps:)
Answer:
this is simple math.
Step-by-step explanation:
easy, mark does have a 5 dollar note, and a litre of milk that costs 80p
he can buy as many as he can, so he buys around;
mark buys over; you divide. By dividing this answer you will get your result. I apologize if this answer didn't help out.
What’s the algebraic expression if you have h more than 8?
Answers
Answer: h+8
Step-by-step explanation:
It’s simple h MORE than 8
Answer: h+8
Step-by-step explanation: