Answers
Answer: 6.96 in^2
Step-by-step explanation:
Trapezoid Area
A = \(\frac{a+b}{2} h\)
= \(\frac{1.5 + 3.3}{2} * 2.9\)
= \(\frac{4.8}{2} * 2.9\)
= 2.4 * 2.9
= 6.96
Related Questions
Ratio..A candy store sells snacks by weight. A six ounce bag of candy cost $3.60. Predict the cost of a 2ounce bag.
Answers
Answer:
A 2 ounce bag costs $1.2.
Step-by-step explanation:
With the information provided, you can use a role of three to find the cost of a 2 ounce bag given that you know that a six ounce bag costs $3.60.
6 ounce bag → 3.60
2 ounce bag → x
x=(2*3.60)/6
x=7.20/6
x=1.2
According to this, the answer is that a 2 ounce bag costs $1.2.
-7u + 10 + -1 + -3u
PLEASE HELP ME
Answers
PLS HELP ME
how do I find x and y? I don't really want the answer but I want to know what to solve in order to get x and y
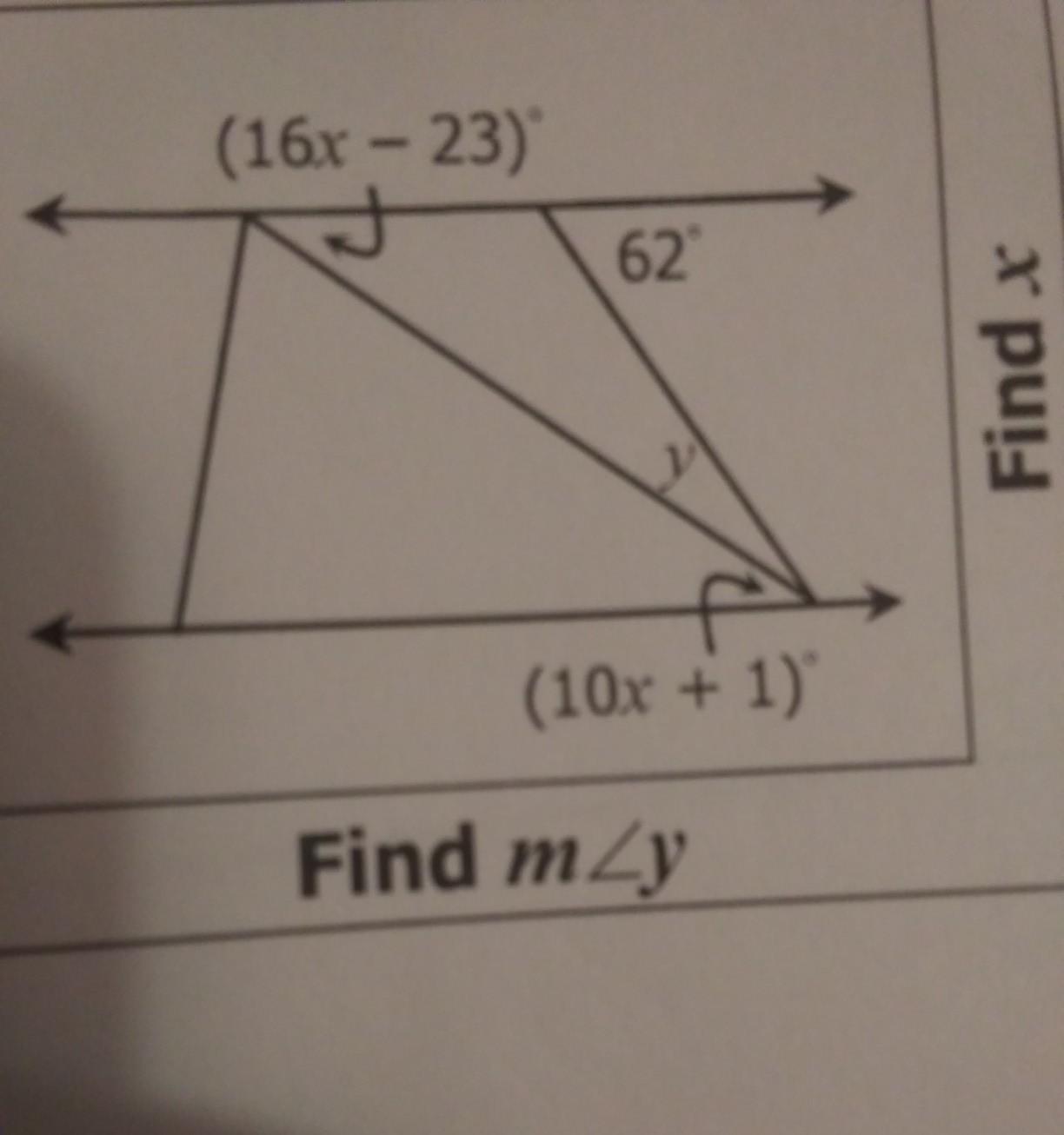
Answers
Answer:
y = 21°
Step-by-step explanation:
both are parallel lines, and that means
16x - 23 = 10x + 1
16x - 10x = 23 + 1
6x = 24
x = 4
---------------------------
taking 16x - 23
16 (4) - 23 = 64 - 23 = 41
both angles value is = 41°
------------------------------------
62° + x = 180
x = 180 - 62 = 118°
----------------------------------
the sum of all the angles inside the triangle is equal to 180°
41° + 118° + y = 180°
y = 21°
4 more than 3 times a number is 5
Answers
Answer:
0.33
Step-by-step explanation:
To solve this, you first write the problem as an algebra equation as follows: 3x + 4 = 5
Then you solve the equation by subtracting 4 from both sides, and then divide both sides by 3. Here is the math to illustrate better:
3x + 4 = 5
3x + 4 - 4 = 5 - 4
3x = 1
3x/3 = 1/3
x = 0.33
Answer = 0.33
number of your answer choice and the answer itself.
2. The point (5,-9) is the image under the translation (x, y) = (x + 4, y - 2). What is the pre-image?
1) (9,-11)
2) (1, -7)
3) (1, -11)
4) (20, 18)
+ Ac
Pear Deck Interactive Slide
Students, write your response!
Answers
Answer:
Answer: (1,-7)
Step-by-step explanation:
since the translation is under (x + 4, y - 2)
the symbols (+ and -) would change so the translation to use would be
(x - 4, y + 2)
so you plug in (5, -9) to the new translation and you get your answer which is (1,-7)
at the city museum child admission is $5.90 and adult admission is $9.90 on Tuesday twice as many adult tickets as child tickets were sold for a total sales of $745.30how many child tickets were sold that day
Answers
To find how many child tickets were sold on Tuesday you must first call:
X= number of child tickets
Y= number of adult tickets
Then you can propose the following equation:
Also, adult tickets sold were double of child tickets so
\(Y=2\cdot X\)Replacing in the equation:
\(\begin{gathered} X\cdot5.90\text{ + (2}\cdot X)\cdot9.90\text{ = 745.30} \\ X\cdot5.90\text{ + 19.80 }\cdot X\text{ = 745.30} \\ 25.70\cdot X\text{ = 745.30} \\ X=29 \\ Y=58 \end{gathered}\)So the child tickets sold that day were 29 tickets.
Help, Answer ASAP; will give brainliest
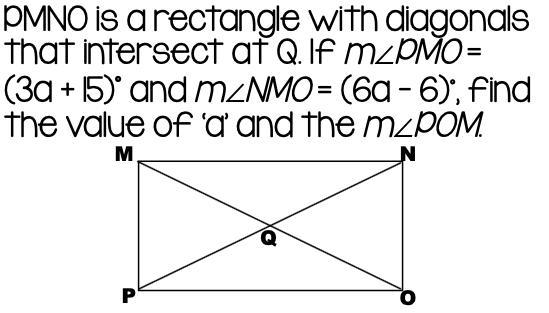
Answers
Answer:
Step-by-step explanation:
measure of a = 9 degree
angle POM = 48 degree = angle NMO [ AIA}
HOPE IT HELPS
Answer:
Below
Step-by-step explanation:
We are given that <PMO= (3a+15)° and NMO= (6a-6)°
Notice that the sum of <PMO and <NMO gives a right angle.
● <PMO+<NMO = 90°
● 3a+15+6a-6 = 90
● 9a + 9 = 90
Substruct 9 from both sides
● 9a +9 -9 = 90 -9
● 9a = 81
Divide both sides by 9
● 9a/9 =81/9
● a = 9
So the value of a is 9°
■■■■■■■■■■■■■■■■■■■■■■■■■■
MN and PO are parallel since MNOP is a rectangle.
MO is crossing MN and PO so <POM and < NMO are alternate interior angles wich means that they have the same size.
● <NMO = <POM
● <POM = 6a-6
The value of a is 9°
● <POM = 6*9-6 = 48°
So <POM = 48°
write the equation of a quadratic function that contains the points (1,21), (2,18), and (-1,9)
Answers
Answer:
The equation of a quadratic function that contains the points (1, 21), (2,18) and (-1, 9) is \(y = -3\cdot x^{2}+6\cdot x +18\).
Step-by-step explanation:
A quadratic function is a second order polynomial of the form:
\(y = a\cdot x^{2}+b\cdot x + c\) (1)
Where:
\(x\) - Independent variable.
\(y\) - Dependent variable.
\(a\), \(b\), \(c\) - Coefficients.
From Algebra we understand that a second order polynomial is determined by knowing three distinct points. If we know that \((x_{1}, y_{1}) = (1, 21)\), \((x_{2},y_{2}) = (2,18)\) and \((x_{3}, y_{3}) = (-1, 9)\), then we construct the following system of linear equations:
\(a+b+c = 21\) (2)
\(4\cdot a + 2\cdot b + c = 18\) (3)
\(a - b + c = 9\) (4)
By algebraic means, the solution of the system is:
\(a = -3\), \(b = 6\), \(c = 18\)
Therefore, the equation of a quadratic function that contains the points (1, 21), (2,18) and (-1, 9) is \(y = -3\cdot x^{2}+6\cdot x +18\).
What is the 9th term of the following sequence?
243, 81, 27, 9, ...
SHOW ALL WORK PLEASE
Answers
9/3 = 3
3/3 = 1
1/3 = 0.333
0.333/3 = 0.111
0.111/3 = 0.037
0.037/3 = 0.012
0.012/3 = 0.0041
0.0041/3 = 0.00137
0.00137/3 = 0.000457
BELL RINGER #2
A consultant charges $45 for each hour she works on a consultation, plus a flat $30
consulting fee. How many hours of work are included in a $210 bill for a consultation?
A. 2 4/5
B. 4
c. 4 2/3
D. 5 1 / 2
E. 7
Answers
Answer:
A. 2 4/5
Step-by-step explanation:
To find how many hours she worked for $210, you must get the amount of money she gets in 1 hour.
Because she charges $43 dollars every hour, and fines a fee of $30 flat, we must add both of the amount to get how many she earns in 1 hour.
So:
$45 + $30= $75
She earn $75 in 1 hour.
Next, divide $210 dollars that she earned for working for hour(s) to the amount of money she earned in 1 hour to find how many hours she worked.
So:
$210 ÷ $75= 2.8 hours
The answer is 2.8 hours
Because the given answers is in fraction, we must change the decimal into a fraction.
To change a decimal into a fraction, you must place the decimal over its place value.
Because 8 in the decimal 2.8 is in the tenths place, you must place it over 10
So:
2.8 into a decimal is 2 8/10
Simplify (only simplify if possible):
Divide 8 and 10 to their GCF which is 2.
So:
8 ÷ 2= 4
10 ÷ 2= 5
So the fraction and the answer is now:
2 4/5
I hope this helps! I'm sorry if it's wrong and too complicated.
a sample from a refuse deposit near the strait of magellan had 60% of the carbon-14 of a contemporary sample. how old was the sample. round to the next whole year.
Answers
The age of the decaying sample according to the decay formula is 42,009 years.
The rate of radioactive carbon-14 decay depends on the function
\(A(t) = A_{0} e^{-0.0001216t}\)
where \(A_{0}\) is the quantity found in living plants and animals, t is in years, and is the age.
60% of the carbon-14 of a current-day sample was present in a sample taken from a refuse deposit close to the Strait of Magellan. We need to evaluate the age of the sample,
A = 60 % of \(A_{0}\) = (3/5)\(A_{0}\)
Putting this in the decay equation, we have,
\(\frac{3}{5} A_{0} = A_{0} e^{-0.0001216t}\\\\ 0.6= e^{-0.0001216t}\\ \\ln0.6 = -0.00001216t\\\\-0.51082 = -0.00001216t\\\\t = 42,008.68\)
Thus, the age of the sample is 42,009 years.
To read more about the decay formula, visit https://brainly.com/question/13720265
#SPJ4
how many ways are there to seat six people around a cir- cular table where two seatings are considered the same when everyone has the same two neighbors without re- gard to whether they are right or left neighbors?
Answers
the number of distinct seating arrangements when two seatings are considered the same when everyone has the same two without neighbors regard to whether they are right or left neighbors is:5!6⋅2=10.6⋅25! = 10
There are $(6-1)! = 5! = 120$ ways to seat six people around a circular table if the seatings are considered distinct. However, we must divide this number by $6$ to account for the fact that rotations of the same seating arrangement are considered the same. We also must divide by $2$ to account for the fact that reflections (i.e., reversing the order of people) of the same seating arrangement are also considered the same.
Therefore, the number of distinct seating arrangements when two seatings are considered the same when everyone has the same two neighbors without regard to whether they are right or left neighbors is:
5!6⋅2=10.6⋅25! = 10
learn more about number here
https://brainly.com/question/10547079
#SPJ4
A robot moves in the positive direction along a straight line so that
after t minutes its distance is s=6t^(4) feet from the origin. (a) Find
the average velocity of the robot over the interval 2,4. (b) Find the
instantaneous velocity at t=2.
Answers
The robot moves in the positive direction along a straight line so that after t minutes its distance is s=6t^4 feet from the origin. (a) Find the average velocity of the robot over intervals 2, 4. We have the following data: Initial time, t₁ = 2 min.
Final time, t₂ = 4 min.The distance from the origin is given by s = 6t^4Therefore, s₁ = s(2) = 6(2^4) = 6(16) = 96 feet s₂ = s(4) = 6(4^4) = 6(256) = 1536 feet
We can find the average velocity of the robot over the interval 2, 4 as follows: Average velocity = (s₂ - s₁) / (t₂ - t₁)Average velocity = (1536 - 96) / (4 - 2)Average velocity = 1440 / 2Average velocity = 720 feet per minute(b) Find the instantaneous velocity at t=2.To find the instantaneous velocity at t = 2 min, we need to take the derivative of the distance function with respect to time. We have the distance function as:s = 6t^4 Taking derivative of s with respect to t gives the velocity function:v = ds / dt Therefore,v = 24t³At t = 2, the instantaneous velocity is:v(2) = 24(2)³v(2) = 24(8)v(2) = 192 feet per minute Therefore, the instantaneous velocity at t = 2 min is 192 feet per minute.
Learn more about intervals
https://brainly.com/question/11051767
#SPJ11
Can someone answer my question please

Answers
Answer:
do you know how to calculate c
Step-by-step explanation:
How many possible values can be assigned to type "logic"?
a.4
b.5
c.2
d.6
e.3
Answers
The number of possible values that can be assigned to the type "logic" is 2, and the correct answer is option c.2.
In logic, the type "logic" refers to a variable or proposition that can take on one of two possible values: true or false.
These values are commonly denoted as 1 (true) and 0 (false), or alternatively as "T" and "F".
Since the type "logic" can only have two possible values, the correct answer is option c.2.
There are no other valid values for this type.
It is important to note that in some programming languages or systems, additional representations or extensions of logic may exist.
For example, some languages may include a "null" or "undefined" value in addition to true and false.
However, in the context of a basic logic type, the number of possible values remains restricted to two: true and false.
For similar question on possible values.
https://brainly.com/question/26202725
#SPJ8
Use a triple integral to find the volume of the solid enclosed by the paraboloids y = x^2 + z^2 and y = 32 - x^2 - z^2
Answers
The volume of the solid enclosed by the two paraboloids is approximately 1365.34π cubic units.
Here, we have to find the volume of the solid enclosed by the two paraboloids \(y = x^2 + z^2\) and \(y = 32 - x^2 - z^2\),
we need to set up a triple integral in cylindrical coordinates.
In cylindrical coordinates, we have:
x = r cos(θ)
z = r sin(θ)
y = y
The limits of integration for r, θ, and y will depend on the region of integration.
First, let's find the intersection points of the two paraboloids:
\(x^2 + z^2 = 32 - x^2 - z^2\\2x^2 + 2z^2 = 32\\x^2 + z^2 = 16\)
This represents a circular region with radius r = 4 in the x-z plane.
Now, let's find the limits of integration for r, θ, and y:
For r:
Since the circular region has a radius of 4, the limits of r will be from 0 to 4.
0 ≤ r ≤ 4
For θ:
The intersection points form a complete circle in the x-z plane, so the limits of θ will be from 0 to 2π.
0 ≤ θ ≤ 2π
For y:
The lower paraboloid is given by \(y = x^2 + z^2\), and the upper paraboloid is given by \(y = 32 - x^2 - z^2\).
The limits of y will be from the lower paraboloid to the upper paraboloid.
\(x^2 + z^2 \leq y \leq 32 - x^2 - z^2\)
Now, we can set up the triple integral to find the volume V:
V = ∫∫∫ (y) dy dθ dr
V = ∫∫∫ \((r^2 cos^2(\theta) + r^2 sin^2(\theta)) dy d\theta dr\)
V = ∫∫∫ \((r^2) dy d\theta dr\)
V = ∫∫ \((r^2) y|_{(x^2+z^2)}^{(32-x^2-z^2)} d\theta dr\)
V = ∫∫ \((r^2) (32 - 2x^2 - 2z^2) d\theta dr\)
V = ∫ \((32r^2 - 2r^2(x^2 + z^2)) d\theta dr\)
V = ∫ \((32r^2 - 2r^2r^2) d\theta dr\)
V = ∫ \((32r^2 - 2r^4) d\theta dr\)
Now, integrate with respect to θ from 0 to 2π:
V = ∫(0 to 2π) ∫(0 to 4) \((32r^2 - 2r^4)\) dr dθ
Now, integrate with respect to r from 0 to 4:
V = ∫(0 to 2π) \([(32/3)r^3 - (1/3)r^5] |_0 ^4\) dθ
V = ∫(0 to 2π) \([(32/3)(4^3) - (1/3)(4^5)]\) dθ
V = ∫(0 to 2π) [(32/3)(64) - (1/3)(1024)] dθ
V = ∫(0 to 2π) [682.67] dθ
V = 682.67 * (2π) - 682.67 * (0)
V = 1365.34π cubic units
Therefore, the volume of the solid enclosed by the two paraboloids is approximately 1365.34π cubic units.
To know more about Paraboloids visit:
brainly.com/question/14307074
#SPJ12
a sphere of radius r inches is sliced by a plane that is d inches from the center. in terms of r and d, what is the radius of the circle of intersection?
Answers
The cross-sectional area will be π*(y^2-x^2) as area of a circle with radius r is π*r^2.
What is equations?There are many different ways to define an equation.The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions.For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign. Mathematical algebraic equations typically have one or more variables.A linear equation may have more than one variable. A linear equation is an equation in which the highest power of the variable is always 1.This is a second-order equation. In quadratic equations, at least one of the variables should be raised to exponent 2.Hence, The cross-sectional area will be π*(y^2-x^2) as area of a circle with radius r is π*r^2.
learn more about equations click here:
brainly.com/question/25976025
#SPJ4
Kadin and Silas went to a movie that started at 1:55 p.m. and got out at 4:10 pm
How long was the movie?
Answers
The movie should be 2 hours and 15 minutes long.
Answer: My answer would be the movie was 2 hours and 55 minutes long.
Step-by-step explanation: I subtracted 4:10 by 1:55 and got 2:55.
4:10-1:55=2:55
Find the common ratio for the geometric sequence: 4, 20, 100, 500.
Answers
Answer:
common ratio r = 5
Step-by-step explanation:
the common ratio r is the ratio of consecutive terms, that is
r = \(\frac{a_{2} }{a_{1} }\) = \(\frac{20}{4}\) = 5
Mr. Evans rides his bicycle an average speed of 8 km/hr. How far has he
traveled if he rides 4 hours?
Answers
Select the correct answer. What would be the value of $150 after eight years if you earn 12 percent interest per year? a. $371. 39 b. $415. 96 c. $465. 88.
Answers
The value will be $371.39.
What is compound interest?Compound interest is the interest you earn on interest. This can be illustrated by using basic math: if you have $100 and it earns 5% interest each year, you'll have $105 at the end of the first year. At the end of the second year, you'll have $110.25.
The formula to calculate the compound amount after t years is given by :-
A =P \((1 + R)^{T}\)
where the interest rate is r and P represents the principal amount.
Given: $150 is the principal sum.
Interest is charged at a rate of 12%/0.12
A = 150 will be the amount compounded after 8 years.
A = 150 \(( 1 + 12 )^{8}\)
A =371.3944
A = $371.39
Hence, the value of $150 after eight years if you earn 12 percent interest per year would be $371.39.
option a. is right
To know more about compound interest click the link:
brainly.com/question/18456266
#SPJ4
Sam finds that the area of a square measured in yards is 16. How could the this measurement be written? Check all that apply.
Answers
Answer:
4 yards
Step-by-step explanation:
Given data
Area of square =16 square yards
We know that area of square is
Area =l²
16=l²
l= √16
l=4 yards
Hence the dimension of the sides is 4 yards each
Given a circle of radius = 10 m, find the area of a 60 degree sector. Please round to 1 d.p.
Answers
Answer:
Area ~= 52.4 m^2
OR (see image why)
Area ~= 52.3 m^2
Step-by-step explanation:
Use A = pi•r^2 to find the area of the whole circle. For a sector, times that by degrees/360.
Your problem has a 60° sector. 60/360 is 1/6.
Use either, 60/360 or 1/6 times 100pi.
If you use the pi button on the calculator the answer is .1 different than if you use 3.14 for pi in your calculation. The pi button answer is more accurate. See image.

-6(p+8)=36
Algebra two step equation
Answers
Answer:
The value of p = -14
Step-by-step explanation:
Given the equation
\(-6\left(p+8\right)=36\)
Divide both sides by -6
\(\frac{-6\left(p+8\right)}{-6}=\frac{36}{-6}\)
simplify
\(p+8=-6\)
Subtract 8 from both sides
\(p+8-8=-6-8\)
simplify
\(p=-14\)
Therefore,
The value of p = -14
Answer:
p = -14
Step-by-step explanation:
-6 ( p + 8 ) = 36
Solve the brackets.
- 6p - 48 = 36
Add 48 to both sides.
- 6p = 36 + 48
- 6p = 84
Divide both sides by -6.
p = -14
help me pleasee, my brain won't work

Answers
The given fractions have equal value, so Liam is correct.
How to find the equivalent fractions?Equivalent fractions are defined as fractions that have different numerators and denominators but the same value. For example, 2/4 and 3/6 are equivalent fractions because they are both equal to 1/2. A fraction is part of a whole. Equivalent fractions represent the same part of a whole.
Liam is claiming that the fraction -(5/12) is equivalent to 5/-12.
Thus, we can say that:
The fraction -(5/12) can be described as the opposite of a positive number divided by a positive number. A positive number divided by a positive number always results in a positive quotient and its' opposite is always negative.
The fraction 5/-12 can be described as a positive number divided by a negative number which always results in a negative quotient
The fractions have equal value, so Liam is correct
Read more about Equivalent fractions at: https://brainly.com/question/17220365
#SPJ1
which procedure can reduce can reduce problems associated with the use of deception by a researcher? a. debriefing b. random sampling c. random assignment d. using only single-blind studies e. using only double-blind studies
Answers
Reporting on a mission, initiative, or the data obtained from it is known as debriefing. Debriefing can reduce problems associated with the use of deception by a researcher. So option a is correct.
Debriefing is the act of reporting on a mission, project, or the data gleaned from it. After an activity or event, a structured procedure examines the actions performed.
Technically speaking, it refers to a method of active intervention that is specialized and developed into more formal meanings like operational debriefing. It is divided into various categories, including, among others, psychological, military, and experiential debriefing.
The following crucial components are often included in effective debriefings:
1. Active participation that goes beyond merely taking criticism in a passive manner.
2. Developmental aim centred on growth and learning
3. A discussion of particular incidents
4. Information from several sources
To learn more about Debriefing link is here
brainly.com/question/28882792
#SPJ4
Suppose a firm can sell it's output at p per unit and that its production function is given by y = AK∝Lβ, where K > 0 is capital input measured in machine-hours, L > 0 is labor input measured in worker-hours and A,∝, ß > 0 are parameters. The firm is perfectly competitive and the factor prices are r per hour and w per hour. (a) Show by partial differentiation that the production function has the property of increasing marginal productivity of capital (if ∝ > 1) and of labor (if ß > 1). Explain the economic significance of this. Does it explain why we normally assume that a and 3 are less than 1?
Answers
Increasing marginal productivity infers that extra units of capital and labor contribute more to yield, driving productive asset allotment. ∝ and ß < 1 expect reducing returns, adjusting with reality.
The production function has the property of increasing the marginal productivity of capital through Partial Differentiation.To appear that the generation work has to expand the marginal productivity of capital (in case ∝ > 1) and labor (on the off chance that ß > 1), we ought to take fractional subsidiaries with regard to each input calculation. For capital (K), the fractional subsidiary of the generation work is:
\(\dfrac{dy}{dK }= \alpha AK^{(\alpha-1)}L^\beta\)
Since ∝ > 1, (∝ - 1) is positive, which implies that the fractional subordinate \(\dfrac{dy}{dK}\) is positive. This shows that an increment in capital input (K) leads to an increment in yield (y), appearing to expand the marginal efficiency of capital.
Additionally, for labor (L), the fractional subordinate of the generation work is:
\(\dfrac{dy}{dL} = \beta AK^{\alpha}L^{(\beta-1)}\)
Since \(\mathbf{\beta > 1, (\beta-1)}\) it is positive, which implies that the halfway subordinate \(\dfrac{dy}{dL}\) is positive. This demonstrates that an increment in labor input (L) leads to an increment in yield (y), appearing to increase the marginal productivity
The economic importance of increasing marginal productivity is that extra units of capital and labor contribute more to yield as their amounts increment. This suggests that the more capital and labor a firm employments, the higher the rate of increment in yield. This relationship is vital for deciding the ideal assignment of assets and maximizing generation effectiveness.
In most generation capacities, it is accepted that ∝ and ß are less than 1. This presumption adjusts with experimental perceptions and financial hypotheses.
In case ∝ or ß were more prominent than 1, it would suggest that the marginal efficiency of the respective factor increments without bound as the calculated input increments.
In any case, there are decreasing returns to scale, which suggests that as calculated inputs increment, the Marginal efficiency tends to diminish. Therefore, accepting ∝ and ß are less than 1 permits for more reasonable modeling of generation forms and adjusts with the concept of diminishing marginal returns.
Learn more about the Marginal productivity of capital here:
https://brainly.com/question/18492635
#SPJ4
True or false: a local variable is a variable defined inside a function that can only be used inside its function
Answers
Given statement 'a local variable is a variable defined inside a function that can only be used inside its function' is False
A local variable is a type of variable that we declare inside a block or a function, unlike the global variable. They can be used only by the statements that are inside the function or the block of the code. Local variables are not known to functions outside their own.
The variable declared is local within that function that is the declared variable is accessible inside that block itself, it cannot be accessible outside the given function.
Consider the following multiplication function:
ex - void multi()
{
int a = 10, b = 2, c ;
c = a * b ;
cout << c ;
}
int main()
{
cout << "value for c is :"<< c ;
return 0;
}
Here inside the multi function variable a, b, c are declared and initialized inside the function.
Thus, a local variable is defined inside the body of the function and is not accessible outside of the function.
Therefore, given statement 'a local variable is a variable defined inside a function that can only be used inside its function' is False
Learn more about the local variable here:
brainly.com/question/27840441
#SPJ4
Solve the equation in the interval from 510^\circ510 ∘ 510, degrees to 1050^\circ1050 ∘ 1050, degrees. Your answer should be in degrees. \sin(x)=0sin(x)=0
Answers
Answer:
540°, 720° and 900°Step-by-step explanation:
Given equation sin(x) = 0 lying between the interval 510°≤x≤1050°. To find the value of x within this range, we first find the value of from the equation as shown;
sin(x) = 0
taking the arcsin of both sides;
\(sin^{-1}(sinx) = sin^{-1} 0\\x = 0^{0}\)
Since x is positive in the first and second quadrant, in the second quadrant, the value of x will be 180°-0° = 180°
Subsequent value of x equivalent to 0° will be addition of 180° to each previous value gotten. The values of x within the range given are as shown
x1 =0°
x2 = 180°-0° = 180(2nd quadrant)
x3 = 180°+180° = 360°
x4 = 360°+180° = 540°
x5 = 540°+180°=720°
x6 = 720°+180° = 900°
x7 = 900°+180° = 1080°
We can see from the values above that the values of x that falls within the given range are 540°, 720° and 900°. This gives the required answers in degrees.
How to find a quadratic equation with y-intercept and vertex? Explain with examples.
Answers
To find a quadratic equation with the y-intercept and vertex, follow these steps: identify the coordinates of the y-intercept and vertex, substitute them into the general form of the quadratic equation, solve for the coefficients, and substitute the coefficients back into the equation. For example, if the y-intercept is (0, 3) and the vertex is (-2, 1), the quadratic equation would be y = x^2 + x + 3.
To find a quadratic equation with the y-intercept and vertex, we can follow these steps:
Step 1: Identify the coordinates of the y-intercept. The y-intercept has the form (0, c), where c is the y-coordinate.Step 2: Identify the coordinates of the vertex. The vertex has the form (-b/2a, f(-b/2a)), where a, b, and c are the coefficients of the quadratic equation.Step 3: Substitute the coordinates of the y-intercept and vertex into the general form of the quadratic equation, y = ax^2 + bx + c.Step 4: Solve the resulting system of equations to find the values of a, b, and c.Step 5: Substitute the values of a, b, and c back into the general form of the quadratic equation to obtain the final equation.For example, let's say the y-intercept is (0, 3) and the vertex is (-2, 1). We can substitute these coordinates into the general form of the quadratic equation:
3 = a(0)^2 + b(0) + c
1 = a(-2)^2 + b(-2) + c
Simplifying these equations, we get:
c = 3
4a - 2b + c = 1
By substituting c = 3 into the second equation, we can solve for a and b:
4a - 2b + 3 = 1
4a - 2b = -2
2a - b = -1
By solving this system of equations, we find a = 1 and b = 1. Substituting these values back into the general form of the quadratic equation, we obtain the final equation:
y = x^2 + x + 3
Learn more:About quadratic equation here:
https://brainly.com/question/30098550
#SPJ11
To find a quadratic equation with a given y-intercept and vertex, you need the coordinates of the vertex and one additional point on the curve.
Start with the standard form of a quadratic equation: y = ax^2 + bx + c, where a, b, and c are constants.Use the vertex form of a quadratic equation: y = a(x - h)^2 + k, where (h, k) represents the coordinates of the vertex.Substitute the vertex coordinates (h, k) into the equation to obtain the equation in vertex form.Use the y-intercept to find another point on the curve. The y-intercept has the form (0, c), where c is the value of y when x is zero.Substitute the coordinates of the additional point into the equation to obtain a system of two equations. Solve the system to find the values of a, b, and c.Substitute the determined values of a, b, and c into the standard form of the quadratic equation to obtain the final equation.Example:
Suppose we want to find a quadratic equation with a y-intercept of (0, 4) and a vertex at (2, -1).
Using the vertex form, we have y = a(x - 2)^2 - 1.Substituting the y-intercept coordinates, we get 4 = a(0 - 2)^2 - 1, which simplifies to 4 = 4a - 1.Solving the equation above, we find a = 1.Substituting the values of a and the vertex coordinates into the vertex form equation, we have y = 1(x - 2)^2 - 1.Expanding the equation and simplifying, we get y = x^2 - 4x + 3.The final quadratic equation with the given y-intercept and vertex is y = x^2 - 4x + 3.To find a quadratic equation with a given y-intercept and vertex, you can use the vertex form of a quadratic equation and substitute the coordinates to obtain the equation. Then, use the y-intercept to find an additional point on the curve and solve a system of equations to determine the coefficients. Finally, substitute the coefficients into the standard form of the quadratic equation to get the final equation.
To know more about quadratic equation visit:
https://brainly.com/question/30164833
#SPJ11
