104
5
-10
-6
10
N
-10*
Given the graphs of f(x) = 3x - 3 and g(x) = -x + 5, which statements are true?
A)
The system has two solutions.
B)
The system has infinitely many solutions.
C)
Point (2, 3) is the only solution.
D)
Any point on either line is a solution.
E)
The point of intersection is the solution.
Answers
Answer:
C
Step-by-step explanation:
Related Questions
9x-3>5x+17
How would i solve this step by step
Answers
Answer:
x > 5
Step-by-step explanation:
add 3 to both sides
9x-3>5x+17
+3 +3
9x>5x+17+3
Simplify
9x > 5x + 20
Subtract 5x from both sides
9x > 5x + 20
-5x -5x
= x = 5
Hope This Helped
1 5/8÷(−1 3/5)
Enter your answer as a mixed number, in simplified form, in the box. plz
Answers
Answer:The answer is -1 1/64
Hope this helps!!
Step-by-step explanation:
Swim flippers are helpful for scuba diving. sam has 40 pairs of flippers that he rents out to customers. thirty percent are currently rented out how many pairs of flippers are currently rented out
Answers
try 13 pairs of flippers
It’s in between 10 and 15
In which quadrant does the point (9 , -13) lie?
A.
Quadrant II
B.
Quadrant III
C.
Quadrant I
D.
Quadrant IV
Answers
Find the sum of the given integers. 7 + (-8) + 2 + (-1) =
Answers
Answer:
0
Step-by-step explanation:
7 + (-8) + 2 + (-1)
is the same as:
7 - 8 + 2 - 1
Simplify these:
-1 + 1
Solve:
0
A cylinder has a height of 5 feet. Its volume is 1,570 cubic feet. What is the radius of the cylinder? Use ≈ 3.14 and round your answer to the nearest hundredth.
Answers
The radius of the cylinder is equal to 10 feet.
How to calculate the volume of a cylinder?In Mathematics and Geometry, the volume of a cylinder can be calculated by using the following formula:
Volume of a cylinder, V = πr²h
Where:
V represents the volume of a cylinder.h represents the height of a cylinder.r represents the radius of a cylinder.By substituting the given parameters into the formula for the volume of a cylinder, we have the following;
V = πr²h
1,570 = 3.14 × r² × 5
1,570 = 15.7r²
r² = 1,570/15.7
r² = 100
Radius, r = √100
Radius, r = 10 feet.
Read more on cylinder here: brainly.com/question/14060443
#SPJ1
help me please if you can

Answers
Answer: XYVW
Step-by-step explanation:
Answer:
hmm maybe try the statement XYVW
A. 5°
B. 35°
C. 31°
D. 7°
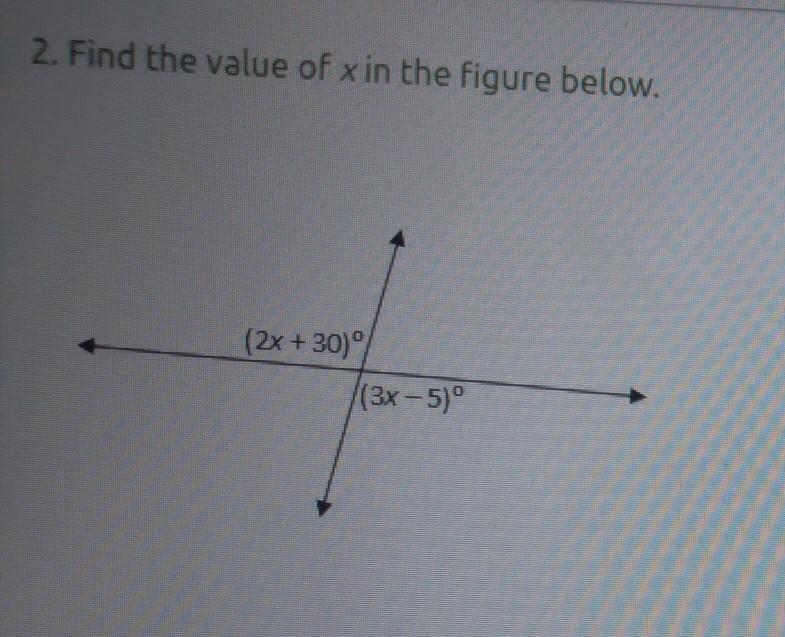
Answers
Answer:
(2x +30) and (3x -5) (they're opposite to eachother, so they're equal)
2x + 30 = 3x - 5 (set them equal to eachother, then subtract 3x from both side)
-1x = -35 (divide both sides by -1 to isolate x)
x = 35 or B (this is your answer)
Step-by-step explanation:
I hope this helps :))
hay 1230 personas, entre hombres y mujeres. Si se sabe que el número de mujeres, supera en 150 al número de hombres. ¿Cuántos hombres están habitando la mini ciudad?
Answers
There are 540 men living in the mini city.
x + (x + 150) = 1230
Simplifying this equation, we get:
2x + 150 = 1230
Subtracting 150 from both sides, we get:
2x = 1080
Dividing both sides by 2, we get:
x = 540
Therefore, there are 540 men living in the mini city.
To check our answer, we can substitute x = 540 into our original equation:
540 + (540 + 150) = 1230
690 = 1230
This is false, so there must be an error in our calculation. We can double-check our work by trying a different approach.
We know that the number of women exceeds the number of men by 150, so we can represent the number of women as (x + 150). We also know that the total number of people is 1230, so we can set up an equation:
x + (x + 150) = 1230
Simplifying this equation, we get:
2x + 150 = 1230
Subtracting 150 from both sides, we get:
2x = 1080
Dividing both sides by 2, we get:
x = 540
For such more questions on mini
https://brainly.com/question/29266607
#SPJ8
Find the exact length of the third side. (Pythagorean Theorem)

Answers
Answer:
3 sqrt(5) =c
Step-by-step explanation:
We can use the pythagorean theorem
a^2 + b^2 = c^2
3^2 + 6^2 = c^2
9+36 = c^2
45 = c^2
Take the square root of each side
sqrt(45) = sqrt(c^2)
sqrt(9)sqrt(5) = c
3 sqrt(5) =c
Integral of 1/(x+cosx)
Answers
The integral is ln|x + cos(x)| + C, where C represents the constant of integration.
To find the integral of the function 1/(x + cos(x)), we can employ a combination of algebraic manipulation and the use of standard integration techniques. Here's the solution:
First, let's rewrite the integral in a slightly different form to simplify the process:
∫(1/(x + cos(x))) dx
We notice that the denominator, x + cos(x), is not amenable to direct integration. To overcome this, we employ a substitution. Let's set u = x + cos(x). Now, differentiate u with respect to x: du/dx = 1 - sin(x).
Rearranging this equation, we get dx = du/(1 - sin(x)).
Substituting these values, the integral becomes:
∫(1/(u(1 - sin(x)))) du
Next, we simplify further by factoring out 1/(1 - sin(x)) from the integral:
∫(1/(u(1 - sin(x)))) du = ∫(1/u) du = ln|u| + C
Replacing u with its original expression, we have:
ln|x + cos(x)| + C
Therefore, the answer to the integral is ln|x + cos(x)| + C, where C represents the constant of integration.
For more questions on integral
https://brainly.com/question/30094386
#SPJ8
How do I divide this?\( \frac{2 {x}^{3} + 3 {x}^{2} + 2 }{x + 2} \)
Answers
From the given problem,
\(\frac{2x^3+3x^2+2}{x+2}\)Using synthetic division to find the quotient of the expression.
Reaarrange first the expression based on the degree from highest to smallest.
As you notice, there is no x^1 term, so we will add 0x.
\(\frac{2x^3+3x^2+0x+2}{x+2}\)Take the coefficients of the numerator then proceed to use the synthetic division.
The coefficients are 2, 3, 0 and 2
The last number at the lower left will be the remainder and the coefficients of the quotient are 2, -1 and 2
This will be :
\(2x^2-x+2-\frac{2}{x+2}\)Note that the remainder is written as r/divisor
r = -2 and the divisor is x+2
Therefore, the answer is :
\(2x^2-x+2-\frac{2}{x+2}\)![How do I divide this?[tex] \frac{2 {x}^{3} + 3 {x}^{2} + 2 }{x + 2} [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/YsNww23lelfTViaAiA4tLfwkNsPrVQXa.jpeg)
PLEASE HELP (WILL GIVE BRAINLIEST)

Answers
Answer:
\( \sqrt{ {13.5}^{2} - {8.6}^{2} } = \sqrt{108.29} = 7 \sqrt{2.21} = \frac{7}{10} \sqrt{221} \)
V = (1/2)(8.6)(.7√221)(22.4) = 1,002.33 square meters
The closest answer is 1,001.73 square meters.
A college student is choosing between data plans for her new cell phone. Both plans include an allowance of 2 gigabytes of data per month. The monthly cost of each option can be seen as a function and represented with an equation:
Option A: A(x)=60
Option B: B(x)=10x+25
In each function, the input, x , represents the gigabytes of data used over the monthly allowance.
1. The student decides to find the values of A(1) and B(1) and compare them. What are those values?
A(1)=
B(1)=
2. After looking at some of her past phone bills, she decided to compare A(7.5) to B(7.5) . What are those values?
A(7.5)=
B(7.5)=
3. Describe each data plan in words.
4. Use graphing technology to graph each function on the same coordinate plane. Explain which plan you think she should choose.
The student only budgeted $50 a month for her cell phone. She thought, "I wonder how many gigabytes of data I would have for $50 if I go with Option B?" and wrote B(x)=50 .
B(x)=50, x=
What is the answer to her question?
Answers
1. A(1) = 60 B(1) = 35
2. A(7.5) = 60 B(7.5) = 100
3. Data plan A is constantly 60 which means no added fees (good for long usage)
Data plan B constantly charges 10 with 25 as an entrance fee (good for short usage)
4. See attached files and read the text in parentheses at question 3
50 = 10x + 25 || 25 = 10x || x = 2.5

The functions for the total cost per month for data use are linear in each of
the given options.
Correct responses;
1. A(1) = 60, B(1) = 352. A(7.5) = 60, B(7.5) = 1003. The monthly charge for Option A fixed. The monthly charge for Option B includes a fixed monthly fee and $10 per gigabyte used.4. Please find attached the combined graph of Option A and Option B. Option B is more affordable when the (extra) data usage is less than 3.5 gigabyte each month.The amount of gigabyte of data the student would have for $50 is 2.5 gigabytes.Methods by which the above values are derivedThe given parameters are;
Both plans data allowance per month = 2 gigabytes
Monthly cost for each option are;
Option A: A(x) = 60 = Constant
Option B: B(x) = 10·x + 25
Solution:
1. The values of A(1) and B(1) are;
A(1) = 60
B(1) = 10 × 1 + 25 = 35
Therefore;
A(1) = $60
B(1) = $35
2. The values of A(7.5), and B(7.5) are;
A(7.5) = 60
B(7.5) = 10 × 7.5 + 25 = 100
A(7.5) = $60
B(7.5) = $100
3. The description of each data plan are;
Option A
The data plan of option A has a fixed charge of $60Option B
The charges on the data plan on option B consist of a fixed monthly charge of $25, and $10 per gigabyte of data used.4. Please find attached the graph of the functions of Option A and Option B. From the graph, the most affordable plan to use based on the data usage are;
Option B; If the data used a month, x < 3.5 gigabytesOption A; If the data used a month, x > 3.5 gigabytesEither Option A or Option B if the data usage per month is exactly 3.5 gigabytesThe amount the student budgets per month = $50
By using Option B, we have;
B(x) = 10·x + 25 = 50
10·x = 50 - 25 = 25
\(\displaystyle x = \frac{25}{10} = 2.5\)
At $50, the amount of gigabyte the student can get is x = 2.5 gigabyteLearn more about linear functions here:
https://brainly.com/question/8627594

What is 318 divided 6
Answers
Answer:
53
Step-by-step explanation:
Answer:
53
Step-by-step explanation:
318/6 = 53
There are 6 groups of 53 in 318
At Silver Gym, membership is $25 per month, and personal training sessions are $40 each. At Fit Factor, membership is $75 per month, and personal training sessions are $30 each. In one month, how many personal training sessions would Sarah have to buy to make the total cost at the two gyms equal?
Answers
Answer:
5
Step-by-step explanation:
You start with each membership for each gym as your starting point, then you add the personal sessions to that number.
Silver Gym: 25 65 105
Fit Factor: 75 105
As you can see, it will take Sarah 5 sessions to have both costs equal
Rewrite the equation 8x + 6x^2 -7=x^2 in standard form and identify a, b, and c.
Answers
Answer:
\(5x^2+8x-7=0\\a=5\\b=8\\c=-7\)
Step-by-step explanation:
The standard form of a quadratic is \(ax^2+bx+c=0\). You need to subtract the x^2 from the right to set the quadratic equal to 0. Then a,b, and c are equal to the values of the coefficients in front of the terms.
If this helped, a brainliest would be greatly appreciated!
How do you determine what bn should be in a limit comparison test and a comparison test? When do you know that the series should use a limit comparison test or a comparison test to find if it is convergent/divergent? Examples would be greatly appreciated
Answers
Step-by-step explanation:
Pick a function that is the same "family". It needs to be a function that you know diverges or converges. So p-series and geometric series are common choices. Often we make the numerators the same so that it's easy to compare.
For example, if you have an = 1 / (n − 1), you would choose bn = 1 / n. Since n − 1 is less than n, we know an is greater than bn. And since we know bn diverges, that means the larger function an also diverges.
Or, if you have an = 1 / (n + 1), we again choose bn = 1 / n. However, comparison test is inconclusive here (an < bn, bn diverges), so we use limit comparison test instead.
lim(n→∞) an / bn
lim(n→∞) 1 / (n + 1) / (1 / n)
lim(n→∞) n / (n + 1)
1
The limit is greater than 0, and bn diverges, so an also diverges.
Let's try something more complicated. Let's say an = e⁻ⁿ / (n + cos²n). The numerator e⁻ⁿ is always less than 1, and the denominator is always greater than n.
If we again choose p-series bn = 1 / n, we know bn > an, and bn diverges, so comparison test is inconclusive. Limit comparison test is possible, but tricky.
But, if we choose geometric series bn = e⁻ⁿ / 1, we know bn > an, and bn converges, so by comparison test, an converges as well.
We can try one more: an = (n² + 2) / (n⁴ + 5). Let's choose bn = (n² + 2) / n⁴ = 1 / n² + 2 / n⁴.
The numerators are the same, but an has a larger denominator, so bn > an. bn is the sum of two p-series which converge, so bn converges. Therefore, an converges.
Which definition best describes a linear pair?
A. A pair of angles that combine to form a straight angle
B. A pair of angles whose sum is 360°
O C. A pair of opposite angles formed by intersecting lines
D. A pair of angles whose sum is 90°
SUBMIT
Answers
Answer:
A or C
Step-by-step explanation:
well, two angles are a linear pair if the angles are adjacent and the two unshared rays form a line. The linear pair postulate states that two angles that form a linear pair are supplementary
Hope this helps
Linear pair example below:

A mathematical model is a simplified description of a system or a process. In your opinion, how are mathematical models helpful? What are the advantages and disadvantages of using a model? In what ways are mathematical models linked to the fields of chemistry, biology, and physics? Cite several examples.
Answers
Given statement solution is :- Mathematical models are extremely valuable tools in various fields, including chemistry, biology, and physics. They offer several advantages: Simplification and abstraction, Prediction and simulation, Cost and time efficiency, Insight and understanding.
Mathematical models are extremely valuable tools in various fields, including chemistry, biology, and physics. They offer several advantages:
Simplification and abstraction: Mathematical models allow complex systems or processes to be represented using simplified mathematical equations or algorithms. This simplification helps in understanding the underlying principles and relationships of the system, making it easier to analyze and predict outcomes.
Prediction and simulation: Models enable scientists to make predictions about the behavior of a system under different conditions. They can simulate scenarios that are difficult or impossible to observe in the real world, allowing researchers to explore various hypotheses and make informed decisions.
Cost and time efficiency: Models can be used to explore different scenarios and test hypotheses in a relatively quick and cost-effective manner compared to conducting real-world experiments. They can help guide experimental design by providing insights into the most relevant variables and parameters.
Insight and understanding: Mathematical models often reveal underlying patterns and relationships that may not be immediately apparent from experimental data alone. They provide a framework for organizing and interpreting data, leading to a deeper understanding of the system being studied.
However, mathematical models also have limitations and potential disadvantages:
Simplifying assumptions: Models are based on assumptions and simplifications, which may not fully capture the complexity of the real-world system. If these assumptions are incorrect or oversimplified, the model's predictions may be inaccurate or misleading.
Uncertainty and error: Models are subject to uncertainties and errors stemming from the inherent variability of the system, limitations in data availability or quality, and simplifying assumptions. It is crucial to assess and communicate the uncertainties associated with model predictions.
Validation and verification: Models need to be validated and verified against experimental data to ensure their accuracy and reliability. This process requires rigorous testing and comparison to real-world observations, which can be challenging and time-consuming.
Mathematical models are closely linked to the fields of chemistry, biology, and physics, providing valuable insights and predictions in these disciplines. Here are some examples:
Chemistry: Mathematical models are used to study chemical reactions, reaction kinetics, and molecular dynamics. One example is the use of rate equations to model the kinetics of a chemical reaction, such as the reaction between reactants A and B to form product C.
Biology: Mathematical models play a crucial role in understanding biological systems, such as population dynamics, gene regulation, and the spread of infectious diseases. For instance, epidemiological models like the SIR (Susceptible-Infectious-Recovered) model are used to simulate and predict the spread of diseases within a population.
Physics: Mathematical models are fundamental in physics to describe physical phenomena and predict outcomes. One well-known example is Newton's laws of motion, which can be mathematically modeled to predict the motion of objects under the influence of forces.
Quantum mechanics: Mathematical models, such as Schrödinger's equation, are used to describe the behavior of particles at the quantum level, providing insights into atomic and molecular structures and the behavior of subatomic particles.
Fluid dynamics: Mathematical models, such as the Navier-Stokes equations, are employed to study the behavior of fluids, including airflow, water flow, and weather patterns.
These examples demonstrate the wide range of applications for mathematical models in understanding, predicting, and simulating various phenomena in the fields of chemistry, biology, and physics.
For such more questions on Advantages of Mathematical Models
https://brainly.com/question/12653211
#SPJ8
Score: 50/10012/20 answeredQuestion 14<>James recently hired a roofer to do some necessary work. On the final bill, James was charged a total of$771. $375 was listed for parts and the rest for labor. If the hourly rate for labor was $66, how many hoursof labor was needed to complete the job?(A) First write an equation you can use to answer this question. Use x as your variable and express anypercents in decimal form in the equation.The equation is(B) Solve your equation in part (A) to find the number of labor hours needed to do the job.Answer: The number of labor hours wasQuestion Help: D Video D Post to forumType here to searchIIE
Answers
Part A:
Let x be the number of hours of labor to complete the job
y be the total amount charged.
Since there is an initial charge of $375 for the parts, and $66 per hour, the total amount charged can be written in the equation
\(y=66x+375\)Part B:
If James was charged a total of $771, then y = 771, solve for x.
\(\begin{gathered} y=66x+375 \\ \\ \text{Substitute }y=771 \\ 771=66x+375 \\ \\ \text{Subtract both sides by }375 \\ 771-375=66x+375-375 \\ 396=66x\cancel{+375-375} \\ 66x=396 \\ \\ \text{Divide both sides by }66 \\ \frac{66x}{66}=\frac{396}{66} \\ \frac{\cancel{66}x}{\cancel{66}}=6 \\ x=6 \end{gathered}\)Therefore, the number of labor hours was 6.
HELPPPP MEEEEEEEEEEEEEEE

Answers
Step 1: Start by subtracting 1 from both sides.
3(2x - 1) = 18
-1 -1
3(2x) = 17
Step 2: Divide both sides by 3.
3(2x) = 17
÷ 3 ÷ 3
2x = 17/3
Step 3: Divide both sides by 2.
2x = 17/3
÷ 2 ÷ 2
x = 17/6
Therefore, x = 17/6.
Step-by-step explanation:
the question it says on the assignment is solve the equation

Answers
It's five miles from Tim's house to Rita's house. Roughly how long is this distance in feet?
Answers
Answer: 26,400 feet
Step-by-step explanation:
If one mile is 5,280 feet, then we multiply the number of miles by that.
So, we would do 5,280 x 5, which equals 26,400 feet.
Please help! I don't understand! :(
Directions:Turn the following expressions in radical form into exponential expressions in fractional form. You do not need to evaluate any of the expressions, just put them in simplest form.

Answers
\(\bold{Hello!}\\\bold{Your~Answer~Is~Below!}\)
______________________________
\(\bold{Solution~Steps:}\)
\(1.)~Simplify~\sqrt[14]{y} :\)
\(\bold{Use~\sqrt[n]{a^x}=a\frac{x}{n}~to~rewrite~\sqrt[14]{y}~in~exponential~fraction~form.}\)\(\bold{\sqrt[14]{y}=y\frac{1}{14} }\)\(2.)~Simplify~\sqrt[y]{5^4} :\)
\(\bold{Use~\sqrt[n]{a^x}=a\frac{x}{n}~to~rewrite~\sqrt[y]{5^4}~in~exponential~fraction~form.}\)\(\bold{\sqrt[y]{5^4}=5\frac{4}{y}}\)\(3.~Simplify~\sqrt{9^3}:\)
\(\bold{Use~\sqrt[n]{a^x}=a\frac{x}{n}~to~rewrite~\sqrt{9^3} ~in~exponential~fraction~form.}\)\(\bold{\sqrt{9^3}=9\frac{3}{2}}\)\(4.)~Simplify~\sqrt[n]{m}\)°\(:\)
\(\bold{Use~\sqrt[n]{a^x}=a\frac{x}{n}~to~rewrite~\sqrt[n]{m}}\)° \(\bold{~in~exponential~fraction~form.}\)\(\bold{\sqrt[n]{m}}\)°\(\bold{=\frac{m}{n}}\)°\(5.)~Simplify~\sqrt{y^2}:\)
\(\bold{Use~\sqrt[n]{a^x}=a\frac{x}{n}~to~rewrite~\sqrt{y^2} ~in~exponential~fraction~form.}\)\(\bold{\sqrt{y^2}=y}\)______________________________
\(\bold{Answers:}\)
\(\bold{1~is~y\frac{1}{14}.}\)\(\bold{2~is~5\frac{4}{y}.}\)\(\bold{3~is~9\frac{3}{2}.}\)\(\bold{4~is~\frac{m}{n}}\)°\(\bold{.}\)\(\bold{5~is~y.}\)______________________________
\(\bold{Hope~this~helps,}\\\bold{And~best~of~luck!}\\\\\bold{~~~~~~-TotallyNotTrillex}\)
What's the negative reciprocal of 5?
Answers
Answer:
-1/5 would be your answer.
Step-by-step explanation:
A financial manageress for a company is considering two competing investment proposals. For each of these proposals, she has carried out an analysis in which she has determined various net profit figures and has assigned subjective probabilities to the realization of these returns. For proposal A, her analysis shows net profits of GHȼ 20,000.00, GHȼ 30,000.00 or GHȼ 50,000.00 with respective probabilities 0.2, 0.4 and 0.4. For proposal B, she concludes that there is a 50% chance of successful investment, estimated as producing net profits of GHȼ 100,000.00, and of an unsuccessful investment, estimated as a break – even situation involving GHȼ 0.00 of net profit. Assuming that each proposal requires the same Ghana cedi investment, which of the two proposals is preferable solely from the standpoint of expected monetary return?
Answers
Answer:
Project B is preferable solely from the standpoint of expected monetary return.
Step-by-step explanation:
Calculations of Expected Returns:
Project A:
Net Profits Probability Expected Returns:
GHȼ 20,000.00 0.2 GHȼ 4,000
GHȼ 30,000.00 0.4 GHȼ 12,000
GHȼ 50,000.00 0.4 GHȼ 20,000
Total Expected Returns GHȼ 36,000
Project B:
Net Profits Probability Expected Returns:
GHȼ 100,000 0.5 GHȼ 50,000
GHȼ 0.00 0.5 GHȼ 0.00
Total Expected Returns GHȼ 50,000
Expected Returns are the returns or income which have been weighed with their probabilities of occurrence. It is used to determine the best outcome given events that have different probabilities of occurring. It is an important measure of returns which helps in deciding the best investment option to pursue.
If 1100 square centimeters of material is available to make a box with a square base and an open top, find the largest possible volume of the box. Round to two decimal places if necessary.
Answers
volume= a^2 * h
area= a^2+4ah
take the second equation, solve for h
4ah=1100-a^2
h=1100/4a -1/4 a now put that expression in volume equation for h.
YOu now have a volume expression as function of a.
take the derivative, set to zero, solve for a. Then put that value back into the volume equation, solve for Volume.
Cited from jiskha
Whenever Deven and Laura owe each other money, they "pay" each other using stickers. They've agreed that a Harry Potter sticker is worth 49 dollars and a Twilight sticker is worth 35 dollars. They can even use stickers as "change" if one person overpays the other. For example, if Deven owes Laura 189 dollars, he can give her 6 Harry Potter stickers ($6 \cdot 49 = 294$ dollars), and she can return 3 Twilight stickers ($3 \cdot 35 = 105$ dollars). This trade is like a transfer of $294-105=189$ dollars. What is the smallest positive debt, in dollars, that can be paid off using sticker trading?
Answers
The smallest positive debt that can be paid off using sticker trading is $7$ dollars.
To find the smallest positive debt that can be paid off using sticker trading, we need to consider the values of the stickers (in dollars) and find the smallest positive amount that can be reached through a combination of these values.
Given that a Harry Potter sticker is worth $49 and a Twilight sticker is worth $35, we can approach this problem using the concept of the greatest common divisor (GCD) of these two values.
The GCD of $49$ and $35$ is $7$. This means that any multiple of the GCD can be represented using these sticker values.
In other words, any positive multiple of $7$ dollars can be paid off using sticker trading.
Therefore, the smallest positive debt that can be paid off using sticker trading is $7$ dollars.
For such more questions on debt
https://brainly.com/question/28929846
#SPJ8
Please help me thank you
